Типы алгоритмов. Способы реализации методы построения

1. Алгоритмы

ТИПЫ АЛГОРИТМОВ
СПОСОБЫ РЕАЛИЗАЦИИ
МЕТОДЫ ПОСТРОЕНИЯ

2. Алгоритм — совокупность действий, необходимых для решения задачи

НГТУ, кафедра АСУ, Лауферман О.В.
Алгоритмы могут быть записаны на:
естественном языке
на языке программирования
с помощью математической или другой символической
нотации
Название алгоритма может, и должно
указывать на его назначение или определять
используемый в нем метод решения

3. ТИПЫ АЛГОРИТМОВ

Детерминированный
НГТУ, кафедра АСУ, Лауферман О.В.
Недетерминированный
Алгоритм моделирования

4. Детерминированные алгоритмы

НГТУ, кафедра АСУ, Лауферман О.В.
Детерминированные алгоритмы
Детерминированные
алгоритмы
всегда
обеспечивают
регулярные
решения.
В
них
отсутствуют
элементы,
вносящие
неопределенность,
для
них
невозможна
произвольность в выборе решений, определяющих
последовательность действий

5. Недетерминированные алгоритмы

являются по природе
недетерминированными, и можно показать, что
для них не существует детерминированного
алгоритма.
НГТУ, кафедра АСУ, Лауферман О.В.
Некоторые
из
задач
Недетерминированный
играм и головоломкам.
Недетерминированный
характер
алгоритм
свойственен
описывает
систематическую процедуру поиска нужного
решения
среди
всех
возможных.
Его
существование в
первую очередь зависит от
построения
множества
потенциальных
решений, в котором содержится искомое

6. Алгоритмы моделирования

НГТУ, кафедра АСУ, Лауферман О.В.
Третий, основной тип алгоритмов, предназначен не
для поиска ответа на поставленную задачу, а для
моделирования сложных систем с использованием
ЭВМ

7. Известные алгоритмы разложения числа на простые множители являются недетерминированными, так как в них используется метод проб

НГТУ, кафедра АСУ, Лауферман О.В.
Известные алгоритмы разложения числа на простые
множители являются недетерминированными, так
как в них используется метод проб и ошибок
Основным фактором при выборе метода для задач,
решаемых с помощью перебора большого числа
возможных вариантов, является суммарное время
нахождения решения.
При решении данной задачи для генерации и
проверки всех вариантов простых множителей
возвраты и повторные попытки не осуществляются.
Такой процесс является эффективным

8.

НАЧАЛО
Ввод
n
n
!=1
n%2=
0
t=n
n = n/2
i = 3, t, 2
НГТУ, кафедра АСУ, Лауферман О.В.
Вывод
2
Pr (i) =
1n%i
=0
n
%i=0
10 = 2*5
12 = 2*2*3
121 = 11*11
151 = 151
20346 = 2*3*3391
n= n/ i
Вывод
i
n !=1
КОНЕЦ

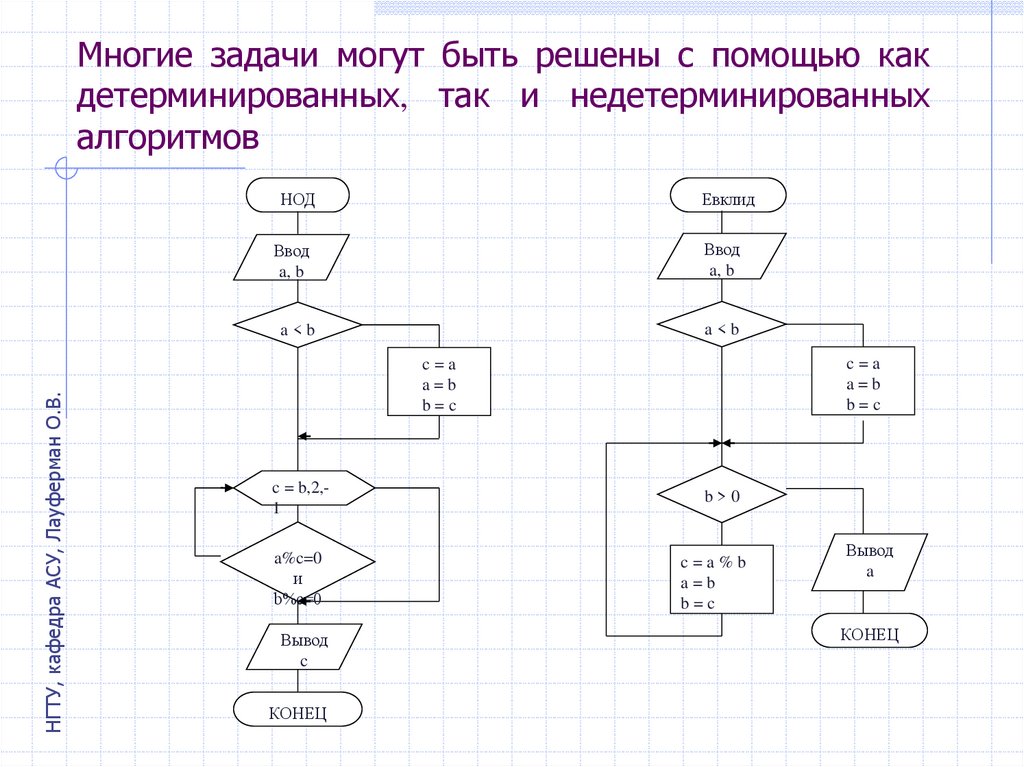
9. Многие задачи могут быть решены с помощью как детерминированных, так и недетерминированных алгоритмов

НОД
Евклид
Ввод
a, b
Ввод
a, b
a<b
НГТУ, кафедра АСУ, Лауферман О.В.
a<b
c=a
a=b
b=c
c=a
a=b
b=c
c = b,2,1
a%c=0
и
b%с=0
Вывод
c
КОНЕЦ
b>0
c=a%b
a=b
b=c
Вывод
a
КОНЕЦ

10. Методы, используемые для сокращения числа вариантов при переборе или позволяющие выбирать наиболее правдоподобные варианты,

называются
НГТУ, кафедра АСУ, Лауферман О.В.
эвристическими
При выборе алгоритма решения задачи в целях
повышения эффективности процесса вычислений
следует
отдавать
предпочтение
детерминированным алгоритмам

11. СПОСОБЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ

Все виды обработки могут быть разделены на
следующие классы:
НГТУ, кафедра АСУ, Лауферман О.В.
последовательная обработка, использующая
повторения
структурное распараллеливание с помощью
сопрограмм
произвольная обработка с применением
параллельных вычислений

12. Существуют две основные формы повторений: итерация и рекурсия

НГТУ, кафедра АСУ, Лауферман О.В.
Итерация в основном используется для тех видов
обработки, которые лучше всего определяются
выражением типа «выполнить для всех Х».
Рекурсия – для получения результирующих
данных, которые легче всего описать рекурсивно, то
есть задать выражением вида «выполнить то же, что
и в последний раз». Текущее действие определяется
с помощью предыдущего ответа или предыдущих
стадий вычислений

13. Пример 1. Классическим примером рекурсии может служить вычисление факториала в следующем виде: n !=1, для n =0; n ! = n*(n-1)!

НГТУ, кафедра АСУ, Лауферман О.В.
Пример 1. Классическим примером рекурсии может
служить вычисление факториала в следующем виде:
n !=1, для n =0;
n ! = n*(n-1)! , для n > 0
int fact_rec (int n)
{
if( n == 0) return 1;
else
return ( n* fact_rec ( n – 1));
}
int fact_iter (int n)
{
int f = 1, k = n;
while ( k > 0 )
{
f = f * k; k --;
}
return f;
}

14. Обе функции имеют линейную сложность. В данном случае итерация предпочтительнее, так как:

вызове содержимое всех
регистров
сохраняется,
а
при
возврате
–
восстанавливается так же, как при любом вызове
подпрограммы.
НГТУ, кафедра АСУ, Лауферман О.В.
При
каждом
рекурсивном
Сохраняются значения всех локальных переменных до
момента возврата, так как они могут быть изменены
вызываемой подпрограммой.
При обычном вызове подпрограмм глубина редко
превышает 6. Глубина рекурсивных вызовов обычно
существенно больше. На практике необходимо убедиться,
что глубина рекурсии не только конечна, но и достаточно
мала

15. Пример 2. Две формы реализации алгоритма нахождения наибольшего общего делителя методом Евклида:

НГТУ, кафедра АСУ, Лауферман О.В.
Пример 2. Две формы реализации алгоритма
нахождения наибольшего общего делителя методом
Евклида:
void Delitel ( int a, int b)
{
if ( b == 0)
{ printf (“ НОД = %d”, a);
return;
}
else
Delitel ( b, a % b);
}
void Evklid ( int a, int b)
{
int c;
while ( b > 0)
{
c = a % b;
a = b;
b = c;
}
printf (“ НОД = %d”, a);
}

16. Пример 3. Числа Фибоначчи определяются с помощью рекуррентного соотношения: F n + 1 = F n + F n – 1, для n > 0 и F 0 = 0, F 1 =

НГТУ, кафедра АСУ, Лауферман О.В.
Пример 3. Числа Фибоначчи определяются с помощью
рекуррентного соотношения:
F n + 1 = F n + F n – 1, для n > 0 и F 0 = 0, F 1 = 1
int Fib_rec ( int n )
{
if ( n == 0) return 0;
if ( n == 1) return 1;
return ( Fib_rec( n - 1) +
Fib_rec( n - 2) ;
}
int Fib ( int n )
{
int i = 1, x = 1, y = 0;
while ( i < n )
{
x = x + y;
y = x – y;
i ++;
}
return x;
}

17. В действительности итерация и рекурсия взаимозаменяемы

НГТУ, кафедра АСУ, Лауферман О.В.
Вывод: следует избегать рекурсии, когда имеется
очевидное итерационное решение поставленной задачи

18. Свойства рекурсивных алгоритмов

НГТУ, кафедра АСУ, Лауферман О.В.
Свойства рекурсивных алгоритмов
Все рекурсивные алгоритмы в целом
имеют ряд свойств, которые объединяют
их с
«рекурсивными структурами
данных»
и
«рекурсивными
определениями»

19. 1.    Рекурсия может быть косвенной

1.
Рекурсия может быть косвенной
программа а ( аргумент х, …)
| b ( f ( x ) ) { f ( x ) – выражение, зависящее от x};
НГТУ, кафедра АСУ, Лауферман О.В.
программа b ( аргумент y, …)
| a ( g ( y ) ) { g ( y ) – выражение, зависящее от y};

20. 2. Объекты, порожденные рекурсивным определением (информационные структуры или вычисления), должны быть конечными

Одна из функций должна иметь следующий общий вид:
Если С то
А прямое
{ действие или выражение, выполняемое
непосредственно}
НГТУ, кафедра АСУ, Лауферман О.В.
Иначе
В рекурсивное { часть, включающая при необходимости
рекурсивные вызовы}
Или
Пока ~ С повторять
В рекурсивное
А прямое

21. 3. Должна существовать управляющая величина m, для того чтобы выполнение соответствующей подпрограммы могло быть завершено

НГТУ, кафедра АСУ, Лауферман О.В.
Это есть целое неотрицательное число, относительно которого
можно сказать, что оно строго убывает при каждом рекурсивном
вызове функции:
Программа Р ( аргументы: n целое; х, у, z, …)
Если n = 0 , то
А прямое ( n, x, y, z, …) {без рекурсивного вызова}
Иначе
В рекурсивное { где все рекурсивные вызовы имеют вид
Р ( n – 1, f(x), g(y), h(z), …) }

22. Общая методика проведения анализа при решении задачи рекурсивным способом содержит три этапа:

НГТУ, кафедра АСУ, Лауферман О.В.
параметризация задачи, заключающаяся в выделении
различных элементов, от которых зависит решение, и в
частности
размерности
решаемой
задачи,
причем
размерность должна (в
благоприятных случаях) убывать
после каждого рекурсивного вызова
поиск тривиального случая и его решение. Зачастую это
ключевой этап алгоритма, который может быть разрешен
непосредственно без рекурсивного вызова. При этом часто
размерность задачи нулевая или равна 1 и т.п.
декомпозиция общего случая, имеющая целью привести
его к одной или нескольким задачам, в основном более
простым (меньшей размерности)

23. Пример 1. Вычисление факториала:

НГТУ, кафедра АСУ, Лауферман О.В.
int fact_rec (int n)
{
// параметризация задачи
if( n == 0) return 1;
// тривиальный случай
else
return ( n* fact_rec ( n – 1));
}
// общий случай

24. Пример 2. Нахождения наибольшего общего делителя методом Евклида:

Пример 2. Нахождения
делителя методом Евклида:
НГТУ, кафедра АСУ, Лауферман О.В.
void Delitel ( int a, int b)
{
if ( b == 0)
{ printf (“ НОД = %d”, a);
return; }
else
Delitel ( b, a % b);
}
наибольшего
общего
// параметризация задачи
// тривиальный случай
// общий случай

25. Пример 3. Формирование чисел Фибоначчи:

int Fib_rec ( int n )
{
НГТУ, кафедра АСУ, Лауферман О.В.
if ( n == 0) return 0;
if ( n == 1) return 1;
return ( Fib_rec( n - 1) +
Fib_rec( n - 2) ;
}
// параметризация задачи
// тривиальный случай
// общий случай

26. Резюме

Последовательное прохождение
рекурсивных алгоритмов:
этапов
построения
НГТУ, кафедра АСУ, Лауферман О.В.
облегчает процесс проектирования и последующего
кодирования
улучшает читаемость программы
сокращает объем программного кода

27. Параллельная обработка может применяться для:

поиска в неупорядоченном массиве с помощью
одновременного доступа ко всем элементам
НГТУ, кафедра АСУ, Лауферман О.В.
для обработки неупорядоченного набора данных
для выполнения операций на различных ветвях
программы и проверки множества различных
вариантов
решений
недетерминированной
задачи
Все эти операции выполняются одновременно
с доступом ко всем элементам

28. Структурное распараллеливание с помощью сопрограмм

НГТУ, кафедра АСУ, Лауферман О.В.
Головная программа
сопрограмме.
передает
управление
её
После этого управление многократно может
переходить от сопрограммы к головной программе,
пока, в конечном счете, не вернется к головной
программе.
При передаче управления сопрограмме последняя
продолжает выполняться с того места, на котором
она была прервана, в отличие от подпрограммы,
которая чаще всего начинает выполняться сначала

29. Сопрограммы, так же как и параллельные процессы, выполняются одновременно

НГТУ, кафедра АСУ, Лауферман О.В.
Их различие между собой заключается в том, что
параллельные процессы стартуют в одно и то же
время и являются равнозначными по важности.
Сопрограммы же состоят из головной программы
и подчиненной ей подпрограммы

30. МЕТОДЫ ПОСТРОЕНИЯ АЛГОРИТМОВ

НГТУ, кафедра АСУ, Лауферман О.В.
При разработке алгоритмов следует использовать
стандартные подходы.
Если метод решения задачи сначала не очевиден, то
проблему следует проанализировать, чтобы точно
определить исходные условия и цели.
Иногда проблему можно разбить
которые проще поддаются решению
на
части,

31. Метод «разделяй и властвуй»

НГТУ, кафедра АСУ, Лауферман О.В.
Некоторые проблемы по природе своей носят
аддитивный характер.
Такие проблемы можно разделить на части, и
решение всей проблемы можно получить с
помощью решения её частей.
При
таком
подходе
параллельную обработку
можно
использовать

32. Метод последовательных приближений (метод подъема)

НГТУ, кафедра АСУ, Лауферман О.В.
Когда известно приближенное решение и есть
способы для его уточнения, можно использовать
данный подход

33. Пример 1. Метод Ньютона-Рафсона для нахождения корней уравнения вида xk – n = 0

НГТУ, кафедра АСУ, Лауферман О.В.
Пример 1. Метод Ньютона-Рафсона для нахождения
корней уравнения вида xk – n = 0
Если требуется найти квадратный корень s из числа
n, то процедура поиска задается следующим
образом:
S k = n / 2, для k = 0, n 0
S k = ½ ( s k-1 + n/ s k-1) для k > 0
Вычисление заканчивается при том значении
индекса k, когда значения s k-1 и s k приблизительно
равны между собой

34. Пример 2. Численное интегрирование

НГТУ, кафедра АСУ, Лауферман О.В.
Пример 2. Численное интегрирование
Для вычисления интеграла отрезок, на котором он
определен, делится на равные части, и на каждой
из
этих частей вычисляется приближение с
помощью значения
f (x k)* x,
где xk – некоторое значение x в пределах k-ой
части, а x – размер каждой из частей отрезка.
Затем производится дальнейшее разбиение
частей на более мелкие отрезки и вычисляется
следующее приближение. Когда два приближения
достаточно близки друг к другу, то решение
найдено

35. Пример 3. Имеется 25 монет. Все они одного веса, за исключением одной монеты с дефектом, которая весит меньше остальных

НГТУ, кафедра АСУ, Лауферман О.В.
Разработайте алгоритм, определяющий фальшивую
монету за три взвешивания.
Каково максимальное число монет, для которых
можно определить монету с дефектом не больше, чем
за три взвешивания на весах с чашками?

36. Метод наискорейшего спуска

НГТУ, кафедра АСУ, Лауферман О.В.
Метод наискорейшего спуска отличается от метода
последовательных приближений тем, что во втором
случае за исходное берется любое приближение,
которое затем улучшается.
В рассматриваемом методе направление каждого
шага планируется так, чтобы он был направлен
в сторону нужного решения

37. Метод наискорейшего спуска и метод подъема

НГТУ, кафедра АСУ, Лауферман О.В.
Метод наискорейшего спуска и метод подъема
Использование метода последовательных приближений
при создании программ заключается в
том, что,
принимая какую-либо программу за исходную,
производится
её
последовательное
улучшение
с помощью отладки и настройки.
Метод
наискорейшего
спуска
нисходящем проектированим и
пошагового уточнения
применяется
при
частично в методе

38. Метод обратного прохода (отрабатывания назад)

НГТУ, кафедра АСУ, Лауферман О.В.
Метод обратного прохода применяется тогда, когда
задан порядок (направление) решения некоторой
задачи, замена этого направления на обратное
может помочь упростить задачу без её изменения.
В методе отрабатывания назад начинаем с цели или
решения и движемся обратно по направлению
к начальной постановке задачи. Затем, если эти
действия обратимы, движемся обратно от
постановки задачи к решению

39. Метод поиска с возвратом (программирование с  отходом назад)

Метод поиска с возвратом (программирование
с отходом назад)
НГТУ, кафедра АСУ, Лауферман О.В.
Метод
можно
описать
как
организованный
исчерпывающий поиск, который часто позволяет
избежать исследования всех возможностей.
Этот метод особенно удобен для решения задач,
требующих проверки потенциально большого, но
конечного числа решений
Любой метод, использующий поиск с возвратом
и попытки повторных решений, можно представить
в виде дерева поиска. При рекурсивном поиске
автоматически
используется
метод
поиска
с возвратом

40. Метод выделения подцелей (метод частных целей)

НГТУ, кафедра АСУ, Лауферман О.В.
Метод
связан
со
сведением
трудной
задачи
к
последовательности более простых задач.
С помощью этих подзадач исходную задачу можно
решить по частям или её упростить и решить

41. Метод выделения подцелей (метод частных целей)

НГТУ, кафедра АСУ, Лауферман О.В.
Использование подхода «разделяй и властвуй» может
служить примером применения метода выделения
подцелей, если, например, процесс решения имеет
следующий вид.
Подцели: разделить задачу на части; решить каждую
часть.
Цель: объединить все частичные решения вместе, чтобы
получить решение всей задачи

42. Метод выделения подцелей (метод частных целей)

В
методе последовательных
используются две подцели.
приближений
также
НГТУ, кафедра АСУ, Лауферман О.В.
Подцели: найти приближенное решение; уточнить его.
Вторая из этих подцелей повторяется до тех пор, пока не
будет получено достаточно точное приближение

43. Метод выделения подцелей (метод частных целей)

НГТУ, кафедра АСУ, Лауферман О.В.
В
методе
наискорейшего
спуска
используется
единственная подцель – продвинуться на один шаг
дальше, и эта подцель повторяется, пока не будет
достигнута такая позиция, из которой дальнейшее
продвижение невозможно.
В методе поиска с возвратом задача решается не путем
разбиения её на части, а с помощью её модификации