Похожие презентации:
Теория алгоритмов
1. Теория алгоритмов
ТЕОРИЯ АЛГОРИТМОВИванилова Т.Н.
19 ноября 2019г.
2. Понятие алгоритма и алгоритмической системы
• Алгоритм – это общий, единообразный,точно установленный способ решения
любой задачи из данной массовой
проблемы.
3. Характеристики алгоритма
Дискретность
Элементарность шагов алгоритма
Детерминированность
Результативность или сходимость
Массовость
4. Алгоритмические модели (системы)
это - формализация понятия «алгоритм».Алгоритмические системы допускают описание
любых алгоритмов.
Выделяют три основных типа универсальных
алгоритмических систем:
• Рекурсивные функции
• Машина Тьюринга
• Канонические системы Поста, нормальный
алгоритм Маркова
5. Машина Тьюринга
состоит из:• управляющего устройства, которое может находиться в
одном из состояний, образующих множество Q={q1, …, qn}
• ленты, разбитой на ячейки, в каждой из которых может быть
записан символ из конечного алфавита A={a1,…, am}
• устройства обращения к ленте – считывающей или пишущей
головки, которая в любой момент времени обозревает ячейку
ленты и, в зависимости от символа в ячейке и состояния
управляющего устройства, записывает в ячейку символ (может
быть совпадающий с прежним или пустой (т.е. стирает)).
Потом сдвигается на ячейку влево или вправо или остается на
месте. При этом управляющее устройство переходит в новое
состояние (или остается в старом). Обозначение - dk= L(R,C)
6.
• внутренняя память машины Тьюринга –это множество состояний
• внешняя память – лента
• Лента бесконечна в обе стороны
7.
• Машина Тьюринга может описываться системой правил(команд), имеющих вид:
• 1) qiaj qi′ aj′ dk
• 2)
aj
qi
qi′ aj′ dk
aj aj′ dk
3) qi
qi′
8.
• Конфигурацией машины Тьюринганазывается ее полное состояние:
внутреннее состояние, состояние ленты,
положение головки.
• Другое название конфигурации машинное слово,
• обозначение этого термина - α1qiα2,
Стандартная начальная конфигурация q1α
Стандартная заключительная конфигурация
qzα.
9. Правильная запись словарного вектора
• α1*α2 * … αk-1 * αk (*-символ–разделитель)• α1 λ α2 λ … αk-1 λ αk (λ – пустой символ).
10.
• Пусть f – функция, отображающая множество векторовнад Аисх в множество векторов над Арез . f: Vисх Wрез ,
где Аисх ,Арез– алфавиты входных и выходных данных.
• Машина Тьюринга правильно вычисляет функцию f,
если
• 1. Для любого vЄ Vисх и w Є Wрез , таких, что f(v)=w,
следует q1v* qz w* (v*, w* - правильные записи v и w)
• 2. Для любого v, такого, что f (v) – не определена,
машина Т с начальной конфигурацией q1v* работает
бесконечно.
11.
• Если для f существует машина Тьюринга,которая правильно ее вычисляет, то f
называется правильно вычислимой по
Тьюрингу
12.
• Будем рассматривать числовые функции,т.е. f:N→N,
• Натуральные числа будем представлять в
единичном (унарном) коде, т.е. А = {1}
либо А = {1, *}, число x представляется
словом 1…1=1x.
13.
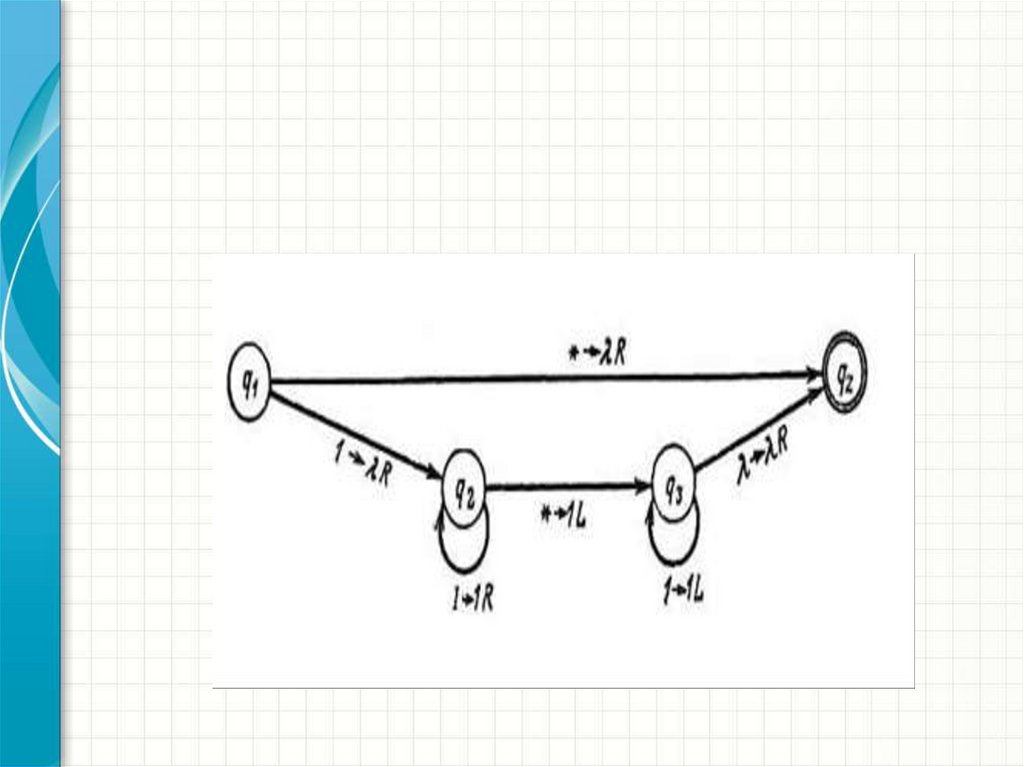
Пример (Сложение, машина Т+)
q1* qzλR
q11 q2λR
q21 q21R
q2* q31L
q31 q31L
q3λ qzλR













 Информатика
Информатика








