Похожие презентации:
Механические свойства твердых тел. Деформации. Практическое занятие 4
1.
Практическое занятие 4Механические свойства твердых тел (ТТ).
Деформации
1
2.
FP C – сила, действующая вдоль оси стержня(деформация растяжения - сжатия)
FИЗ – сила, создающая изгибающий момент.
Зависит от точки приложения силы
(деформация изгиба и сдвига)
FP C
FKP
FИЗ
FKP – сила, создающая крутящий момент.
Зависит от точки приложения силы
(деформация кручения)
2
3.
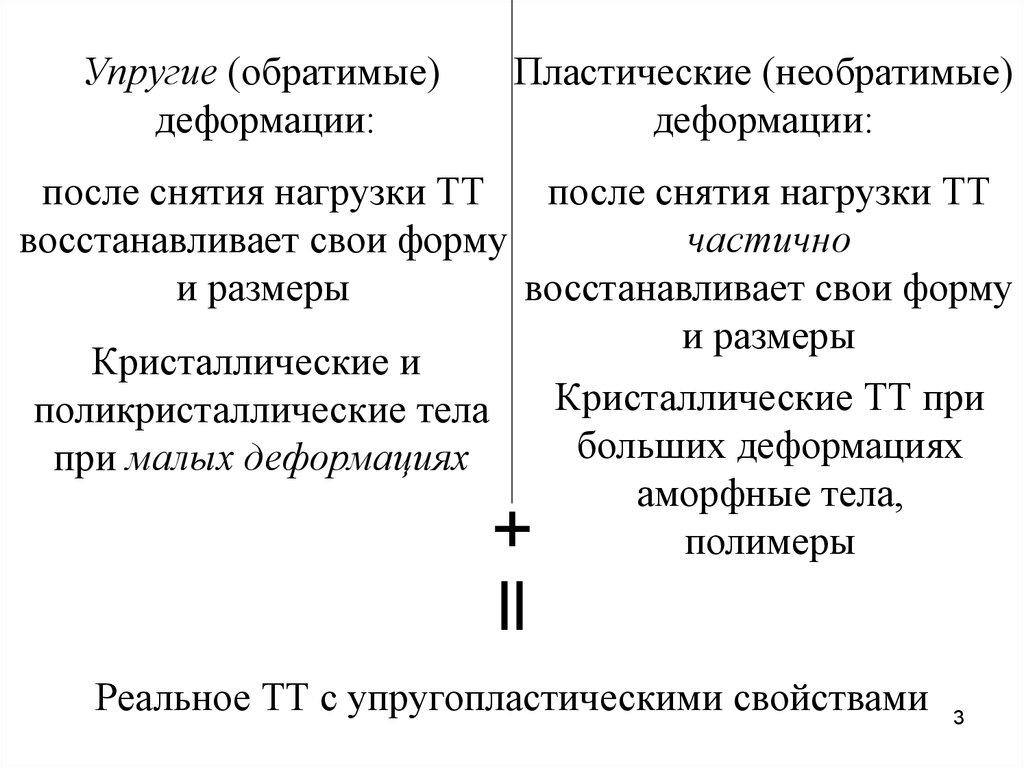
Упругие (обратимые)деформации:
Пластические (необратимые)
деформации:
после снятия нагрузки ТТ
после снятия нагрузки ТТ
восстанавливает свои форму
частично
и размеры
восстанавливает свои форму
и размеры
Кристаллические и
Кристаллические ТТ при
поликристаллические тела
больших деформациях
при малых деформациях
аморфные тела,
полимеры
+
||
Реальное ТТ с упругопластическими свойствами
3
4.
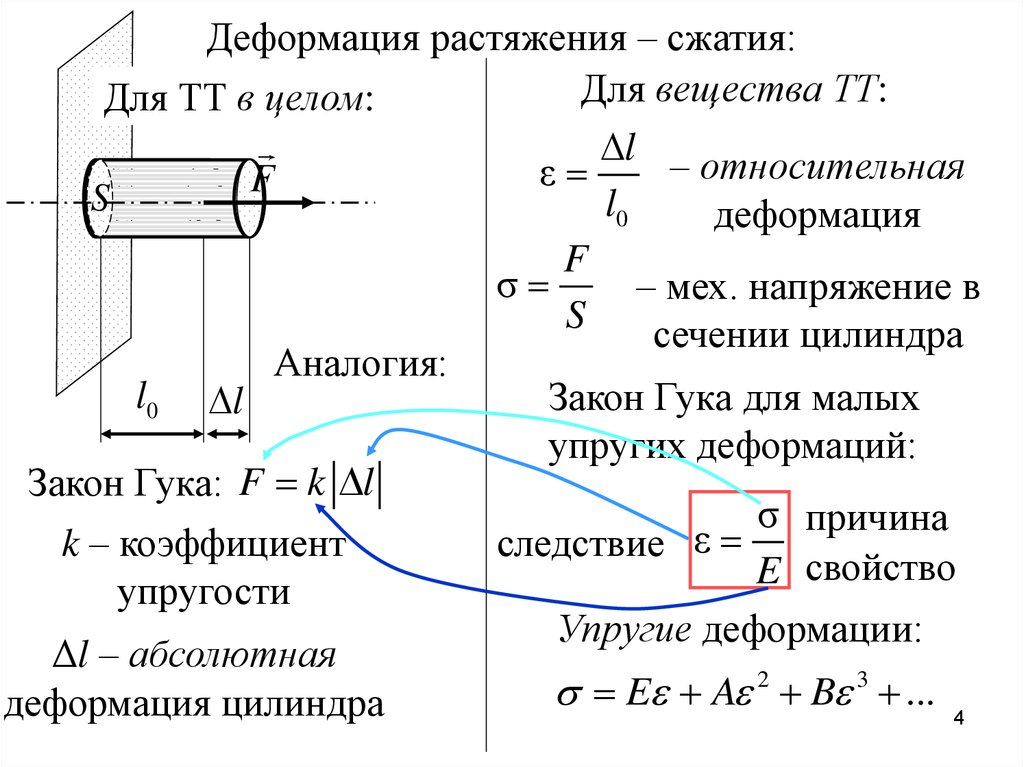
Деформация растяжения – сжатия:Для вещества ТТ:
Для ТТ в целом:
l – относительная
ε
F
S
l0
деформация
F
σ
– мех. напряжение в
S
сечении цилиндра
Аналогия:
l0 l
Закон Гука для малых
упругих деформаций:
Закон Гука: F k l
σ причина
k – коэффициент
следствие ε
E свойство
упругости
Упругие деформации:
Δl – абсолютная
2
3
E
A
B
... 4
деформация цилиндра
5.
1. Сухожилие длиной 16 см под действием силы 12,4 Нудлиняется на 3,3 мм. Сухожилие можно считать
круглым в сечении с диаметром 8,6 мм.
Рассчитать модуль упругости (Юнга) этого сухожилия.
СИ:
F 12,4 H
l0 16 см 0,16 м
l 3,3 мм 3,3 10 3 м
d 8,6 мм 8,6 10 3 м
Закон Гука:
σ
σ
ε E
E
ε
l
F
ε
σ
l0
S
E ?
5
6.
FF l0
4 F l0
S
E
2
l S l πd l
l0
πd 2
S
4
E
4 12,4 0,16
3,14 8,6 10
3 2
3,3 10 3
1,0 10 Па
7
Н м Н
E 2 2 Па
м м м
6
7.
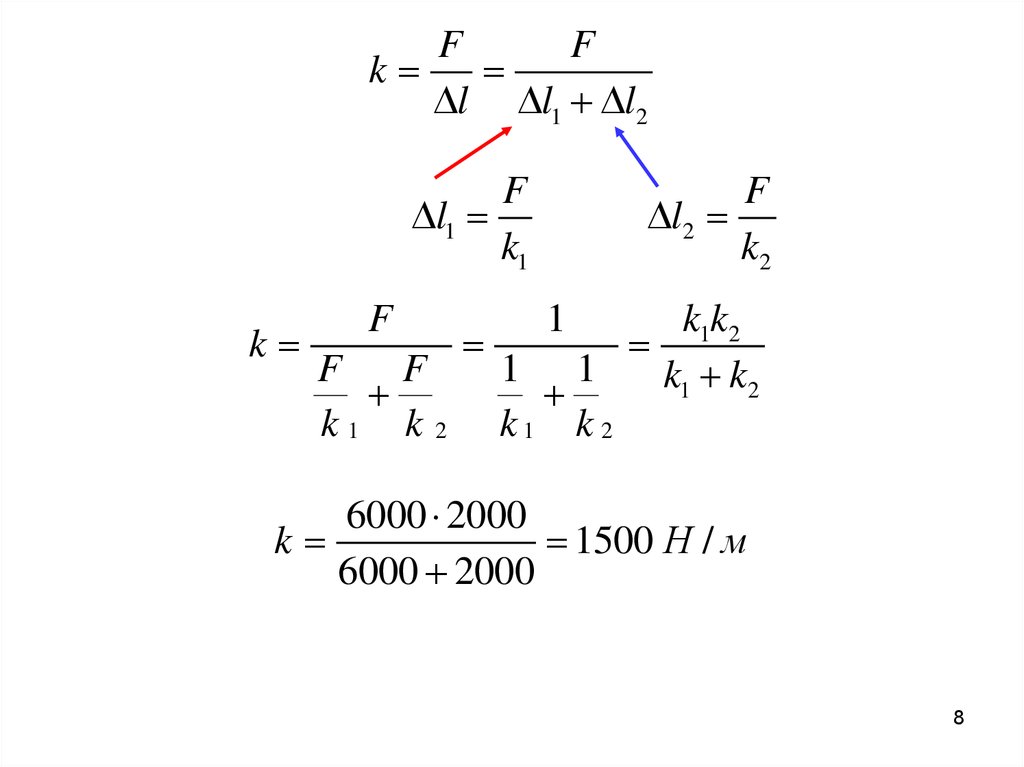
2. Определить жесткость k системы двух пружин припоследовательном и параллельном их соединении.
Жесткости пружин k1=2000 Н/м и k2=6000 Н/м.
2.1. Последовательное соединение:
k1
l01
k2
F
l02
F F1 F2
l1 l01 l1
l2 l02 l2
7
8.
FF
k
l l1 l2
F
l1
k1
F
F
l2
k2
1
k1k2
k
F
F
1 1
k1 k2
k 1 k 2 k1 k 2
6000 2000
k
1500 Н / м
6000 2000
8
9.
2.2. Параллельное соединение:k2
l2 l02 l
l02
F2
F
F
F1
k1
l01
l1 l01 l
F k l F1 F2 k1 l k2 l
k k1 k2
k 2000 6000 8000 Н / м
9
10.
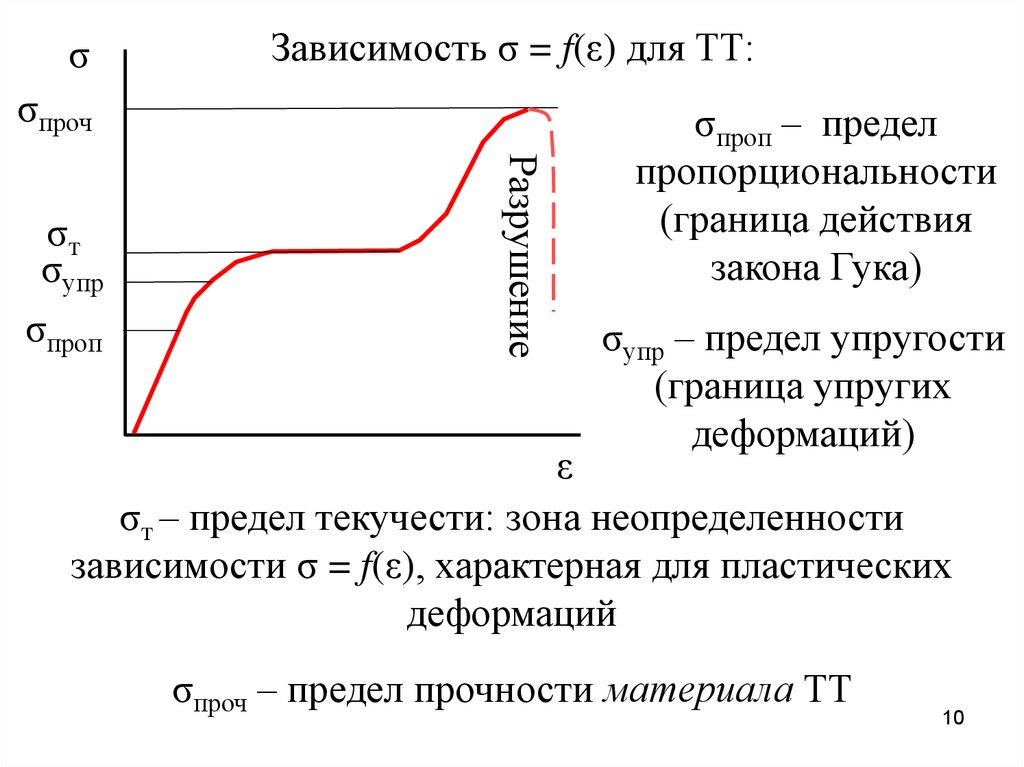
σЗависимость σ = f(ε) для ТТ:
σпроч
σпроп
Разрушение
σт
σупр
σпроп – предел
пропорциональности
(граница действия
закона Гука)
σупр – предел упругости
(граница упругих
деформаций)
ε
σт – предел текучести: зона неопределенности
зависимости σ = f(ε), характерная для пластических
деформаций
σпроч – предел прочности материала ТТ
10
11.
Площадь сечения бедренной кости человека 3,0 см2.Какую силу сжатия может выдержать кость,
не разрушаясь? Предел прочности бедренной кости
при сжатии 124 МПа.
Закон Гука:
СИ:
S = 3,0 см2 = 3,0·10-4 м2
σпроч. = 124 МПа = 124·106 Па
Fmax = ?
F
σ
S
Fmax
σ проч.
Fmax σпроч.S
S
Fmax 124 106 3,0 10 4 372 102 37 кН
11
12.
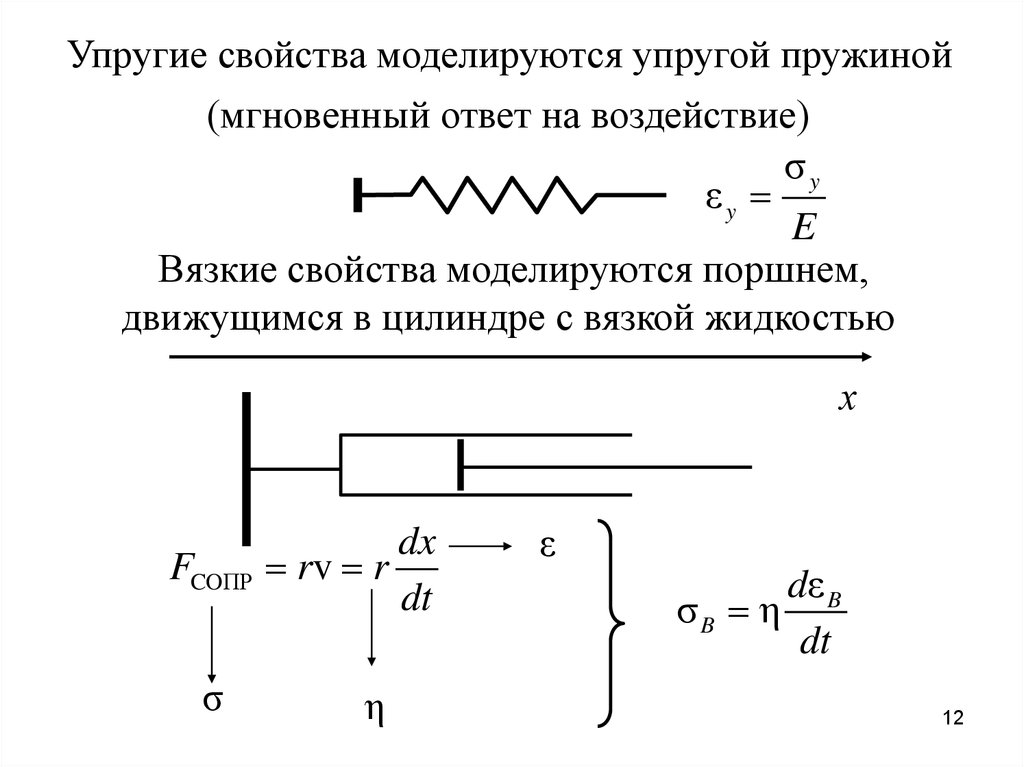
Упругие свойства моделируются упругой пружиной(мгновенный ответ на воздействие)
σy
εy
E
Вязкие свойства моделируются поршнем,
движущимся в цилиндре с вязкой жидкостью
х
FCOΠP
σ
dx
rv r
dt
η
ε
dε B
σB η
dt
12
13.
εу и εВ – упругая и вязкая относительные деформации(в дальнейшем – просто деформации)
σу и σВ – напряжения упругой и вязкой деформаций
r – коэффициент сопротивления вязкой среды
η – коэффициент динамической вязкости среды
(см. Лекция 3)
13
14.
Простейшая комбинация, реализующаявязкоупругие свойства: последовательная модель
Пружина мгновенно растягивается и закрепляется:
Начинается деформация вязкого элемента:
14
15.
Суммарная деформация при последовательномсоединении элементов (задача 2.1):
ε ε y εB
Скорость суммарной деформации:
dε dε y d ε B
dt
dt
dt
Напряжения упругой и вязкой деформаций при
последовательном соединении равны (задача 2.1):
σ y σ B σ const
15
16.
Вязкая:Упругая:
σ
εy
E
dε y
dε B
σ η
dt
1 dσ
dt
E dt
dε B σ
dt
η
Скорость суммарной деформации:
σ = const →
=0
t
σ
0 dε 0 η dt
σ
dε dt
η
d ε 1 dσ σ
dt E dt η
ε
σ
ε t
η
t16
17.
Пружина закреплена:d ε 1 dσ σ
ε = const → dt E dt η
1 dσ
σ
E dt
η
=0
Разделяем переменные и «кучкуем» постоянные:
σ
dσ
E
dt
σ0
σ
η
t
dσ
E
σ 0 η dt
0
σ σ 0e
E
t
η
t
σ – напряжение в элементах в начальный момент времени
(мгновенная деформация и закрепление пружины)17
18.
Параллельная модель:Суммарное
напряжение:
σ σ y σ B const
ε ε y =ε B (см. 2.2)
dε
σ Eε η
dt
Разделение
переменных:
dε
σ Eε η
dt
F const
dt
dε
η σ Eε
18
19.
tt
dt t
t
0 η η η
0
dt
dε
0 η 0 σ Eε
t
ε
ε
dε
1
0 σ Eε E ln σ Eε 0
1 σ Eε
1 Eε
1
ln 1
ln σ Eε ln σ ln
E
σ
E
σ
E
t
1 Eε
ln 1
η
E
σ
E
1 Eε
t ln 1
η
E
σ
19
20.
Потенцирование:e
E
t
η
Eε
1
σ
E
t
σ
η
ε 1 e
E
20
21.
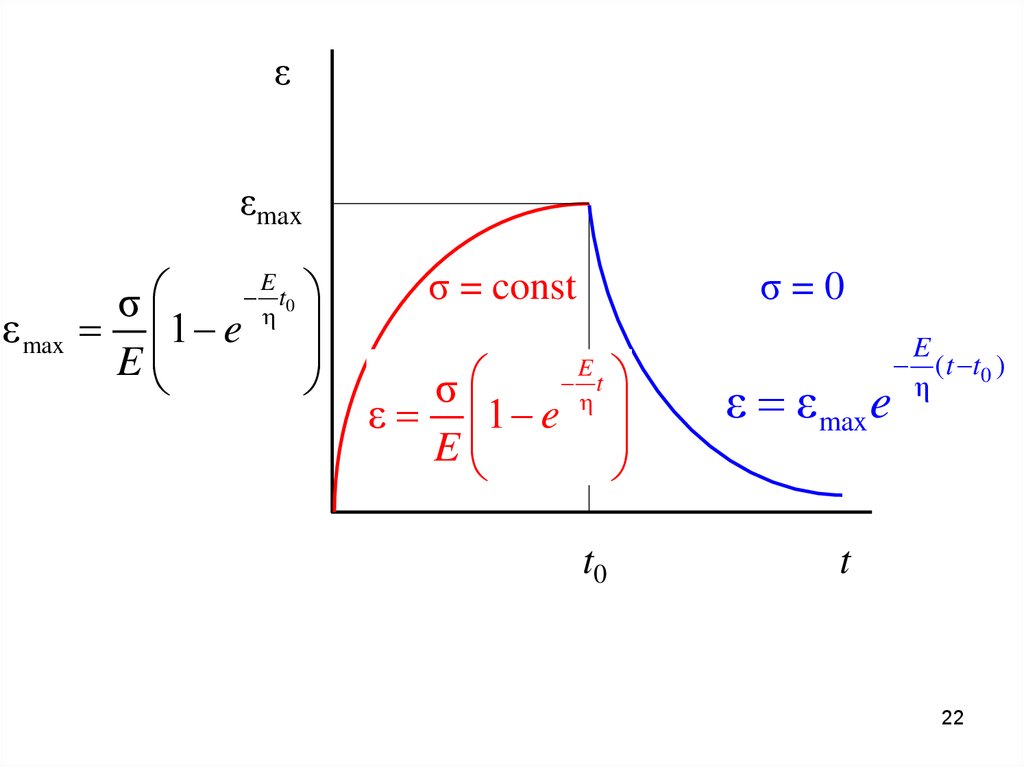
После снятия нагрузки F в момент времени t0при ε = εmax:
σ 0
Пружина начинает сжиматься, перемещая поршень:
dε
0 Eε η
dt
t
E
dε
dt
η t0
max ε
dε
0 Edt η
ε
E
dε
dt
η
ε
dt
ε
E
ε
(t t0 ) ln ε ln ε max ln
η
ε max
ε ε max e
E
( t t0 )
η
21
22.
εεmax
ε max
E
t0
σ
1 e η
E
σ = const
σ=0
E
t
σ
ε 1 e η
E
t0
ε ε max e
E
( t t0 )
η
t
22
23.
Реальная костная ткань0 – 1: быстрая деформация
ε
1 – 2: прямая ползучесть
2
εmax
2 – 3: быстрое сокращение
3 – 4: обратная ползучесть
3 σ=0
1
σ = const
4
0
t0
t
23
24.
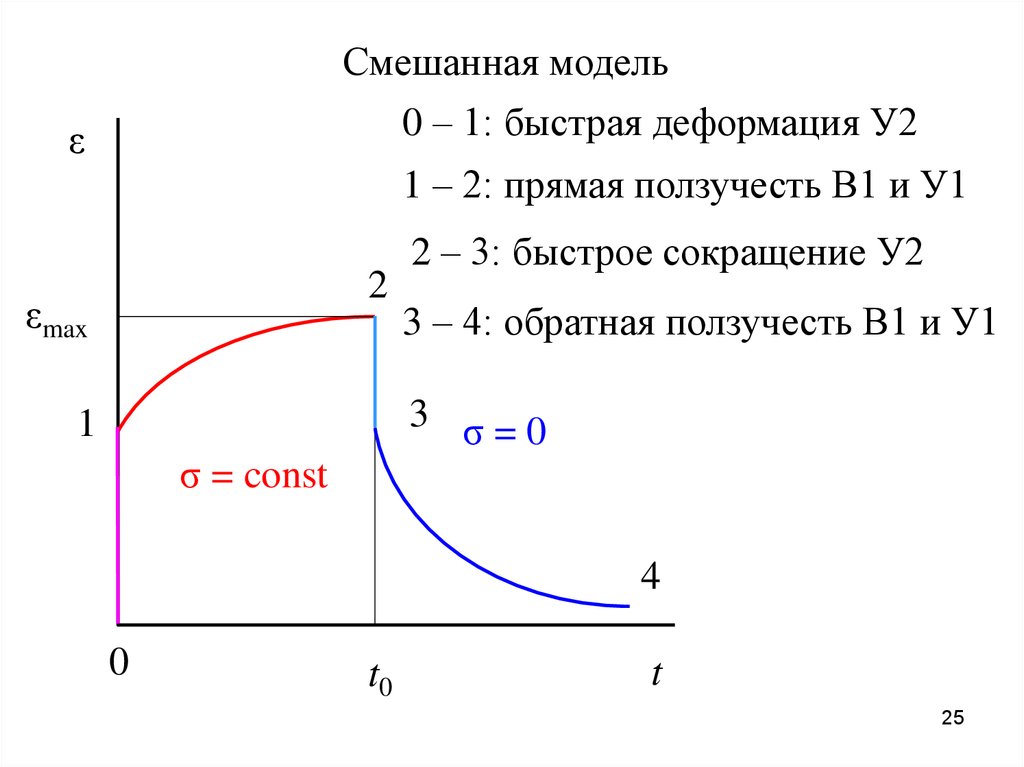
Смешанная модельВ1
У2
У1
24
25.
Смешанная модель0 – 1: быстрая деформация У2
ε
1 – 2: прямая ползучесть В1 и У1
2
εmax
2 – 3: быстрое сокращение У2
3 – 4: обратная ползучесть В1 и У1
3 σ=0
1
σ = const
4
0
t0
t
25
26.
Тема следующего занятия:Поверхностные явления.
Гидростатика.
Гидромеханика идеальной и вязкой жидкости.
Иметь при себе распечатанные выдачи лекции №3
26



















 Физика
Физика








