Похожие презентации:
Параллельность прямых и плоскостей
1.
Решение задач по теме«Параллельность прямых и
плоскостей»
2.
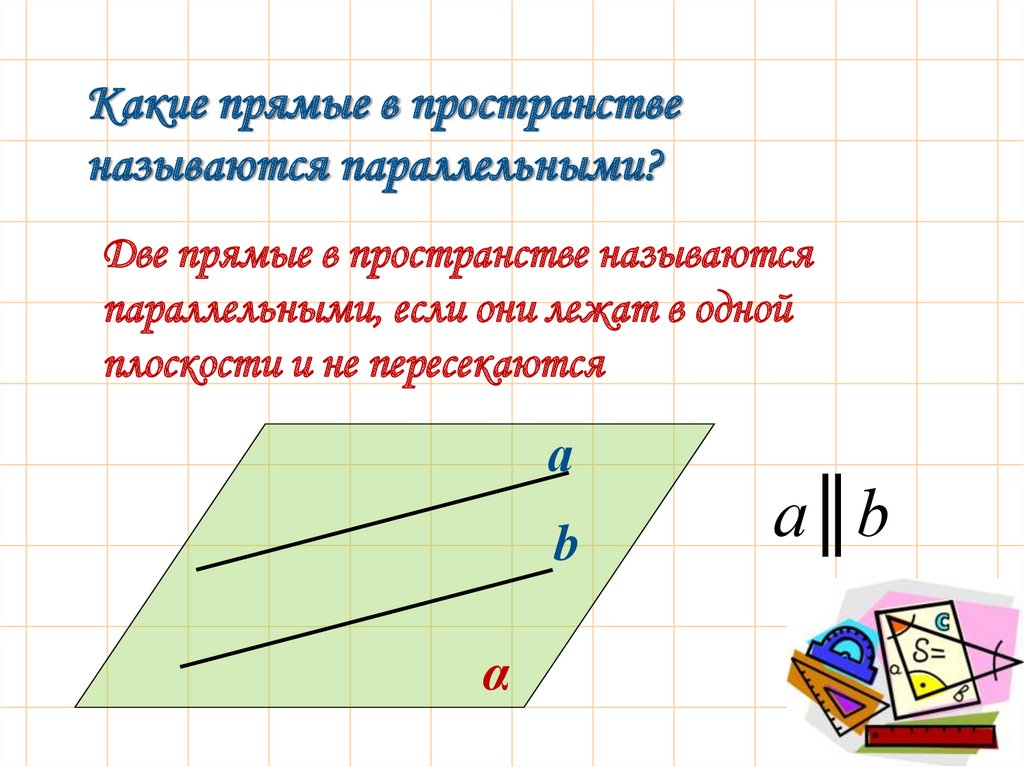
Какие прямые в пространственазываются параллельными?
Две прямые в пространстве называются
параллельными, если они лежат в одной
плоскости и не пересекаются
а
b
α
a║b
3.
Дайте определение скрещивающихсяпрямых.
Прямые, которые не лежат в одной плоскости,
называются скрещивающимися
b
а b
а
α
4.
Когда прямая и плоскость называютсяпараллельными?
Прямая и плоскость называются
параллельными, если они не имеют общих
точек
b
b║α
α
5.
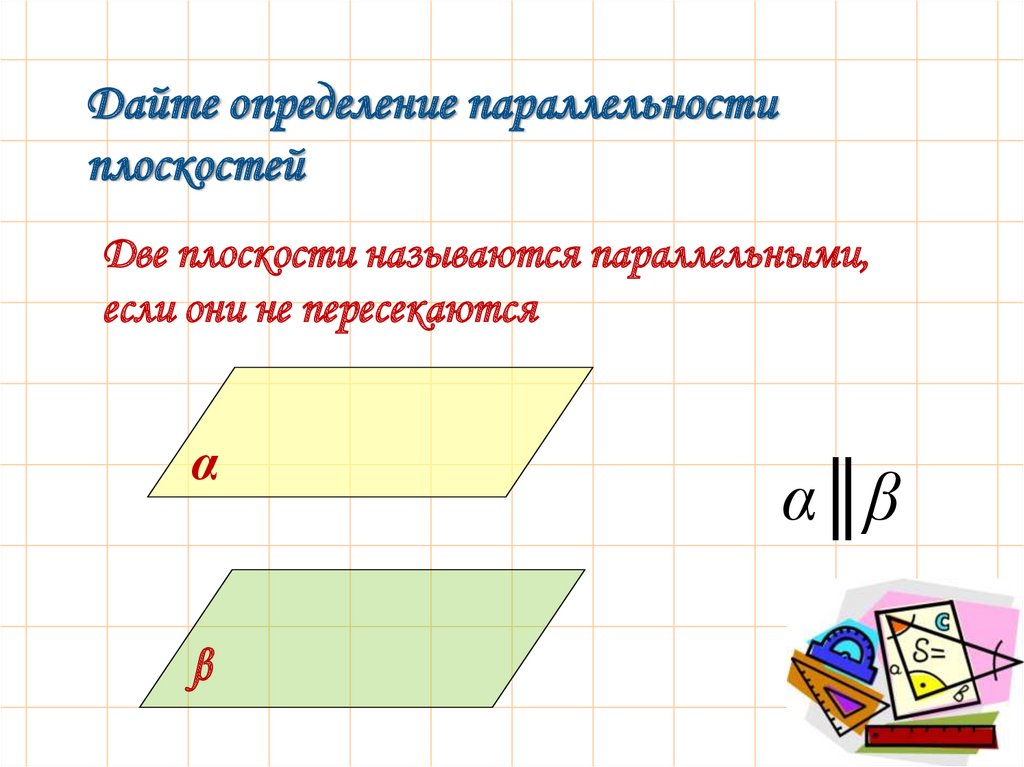
Дайте определение параллельностиплоскостей
Две плоскости называются параллельными,
если они не пересекаются
α
β
α║β
6.
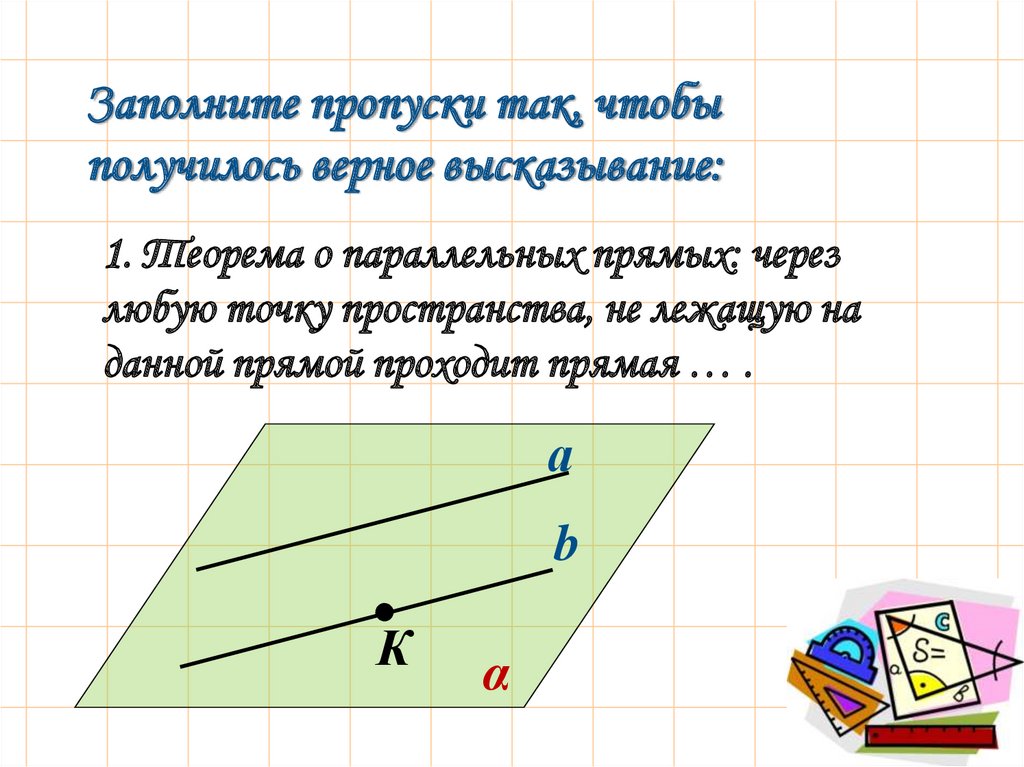
Заполните пропуски так, чтобыполучилось верное высказывание:
1. Теорема о параллельных прямых: через
любую точку пространства, не лежащую на
данной прямой проходит прямая … .
а
b
К
α
7.
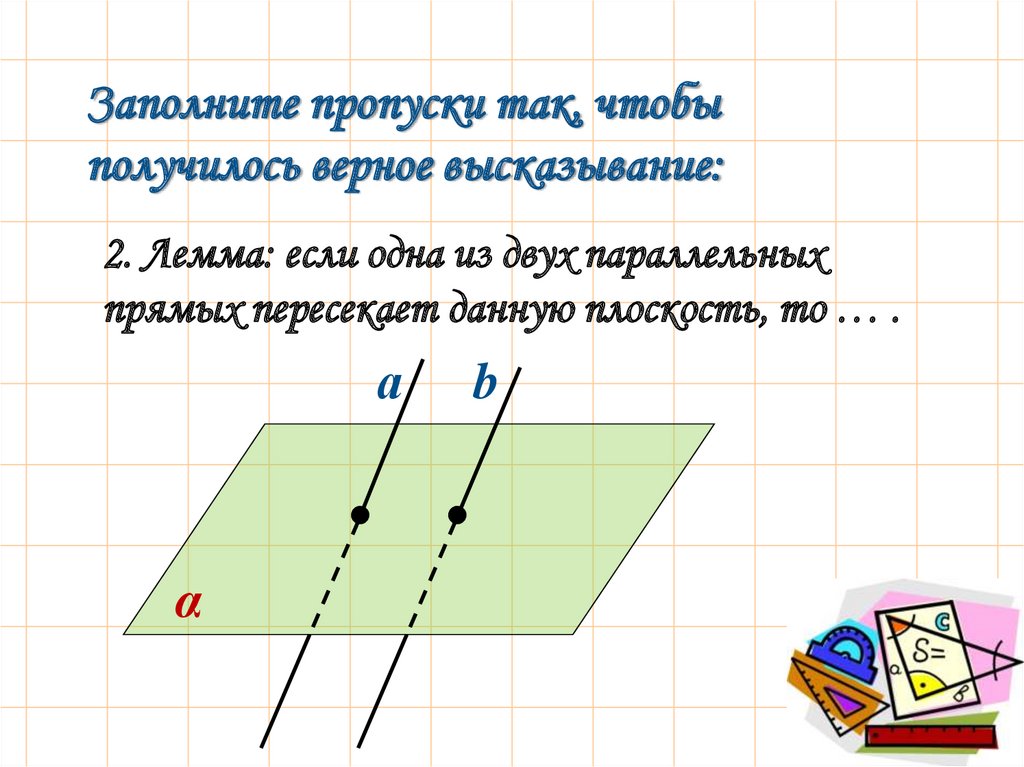
Заполните пропуски так, чтобыполучилось верное высказывание:
2. Лемма: если одна из двух параллельных
прямых пересекает данную плоскость, то … .
а
α
b
8.
Заполните пропуски так, чтобыполучилось верное высказывание:
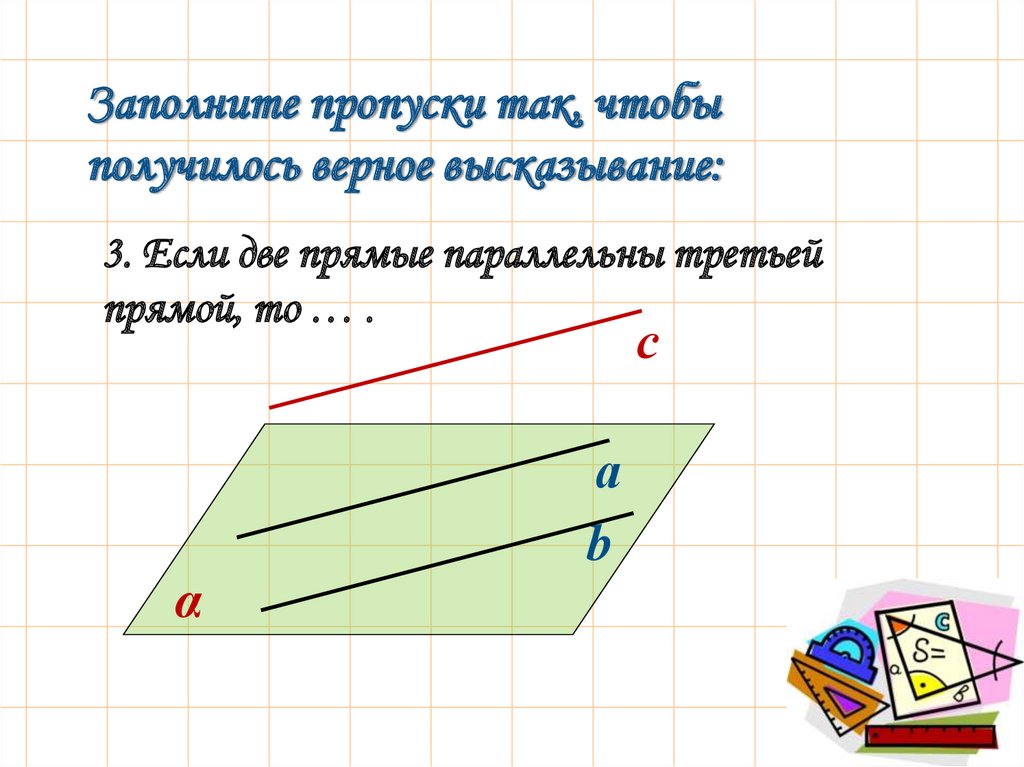
3. Если две прямые параллельны третьей
прямой, то … .
с
α
а
b
9.
Заполните пропуски так, чтобыполучилось верное высказывание:
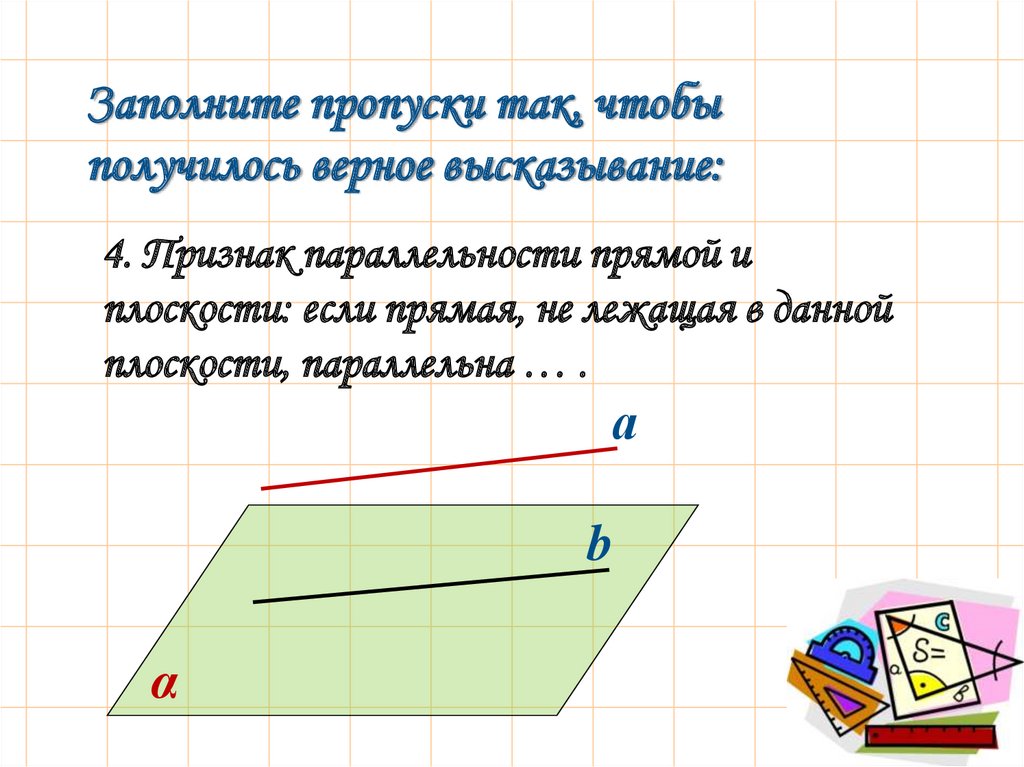
4. Признак параллельности прямой и
плоскости: если прямая, не лежащая в данной
плоскости, параллельна … .
а
b
α
10.
Заполните пропуски так, чтобыполучилось верное высказывание:
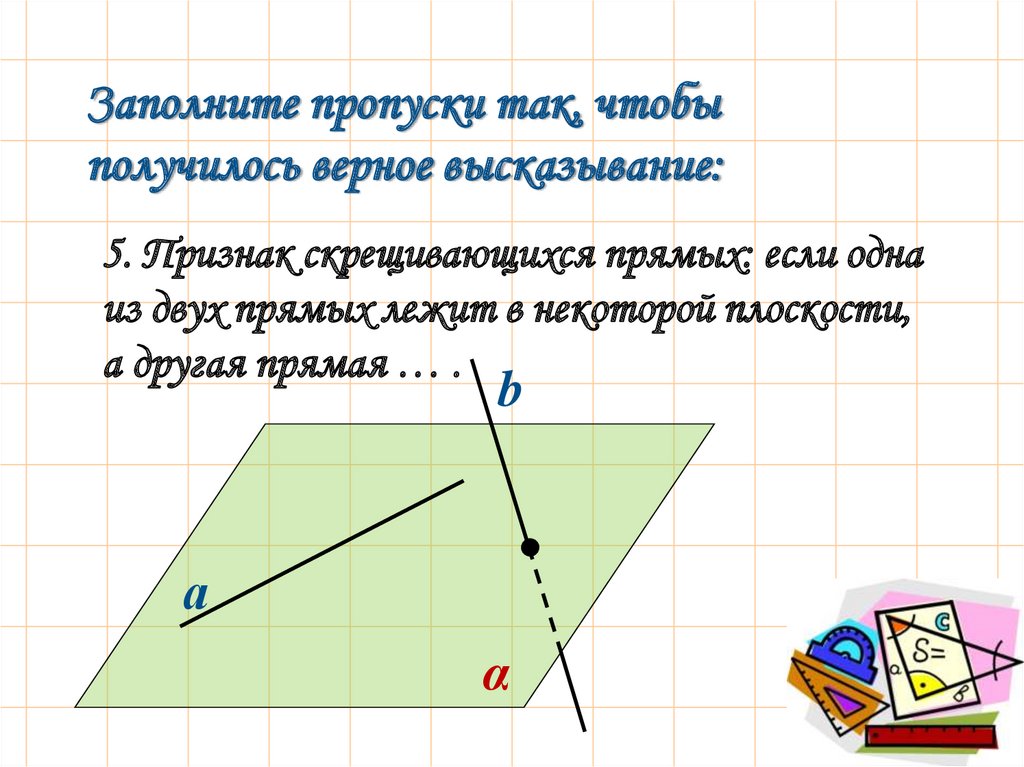
5. Признак скрещивающихся прямых: если одна
из двух прямых лежит в некоторой плоскости,
а другая прямая … .
b
а
α
11.
Заполните пропуски так, чтобыполучилось верное высказывание:
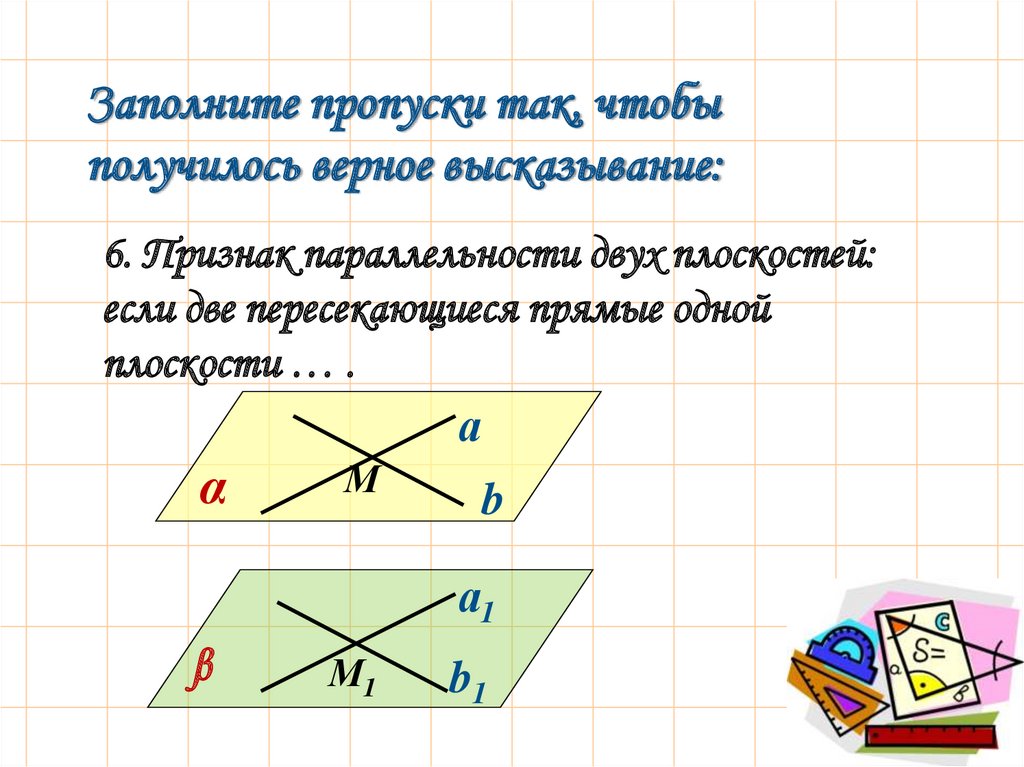
6. Признак параллельности двух плоскостей:
если две пересекающиеся прямые одной
плоскости … .
а
α
М
b
а1
β
М1
b1
12.
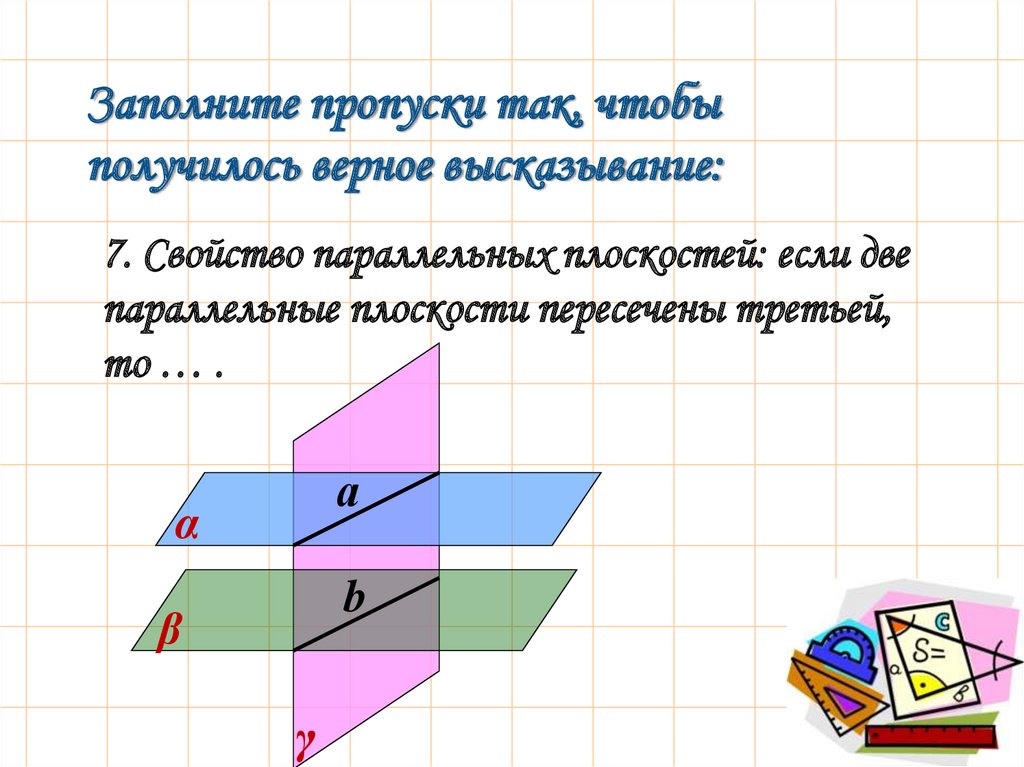
Заполните пропуски так, чтобыполучилось верное высказывание:
7. Свойство параллельных плоскостей: если две
параллельные плоскости пересечены третьей,
то … .
а
α
b
β
γ
13.
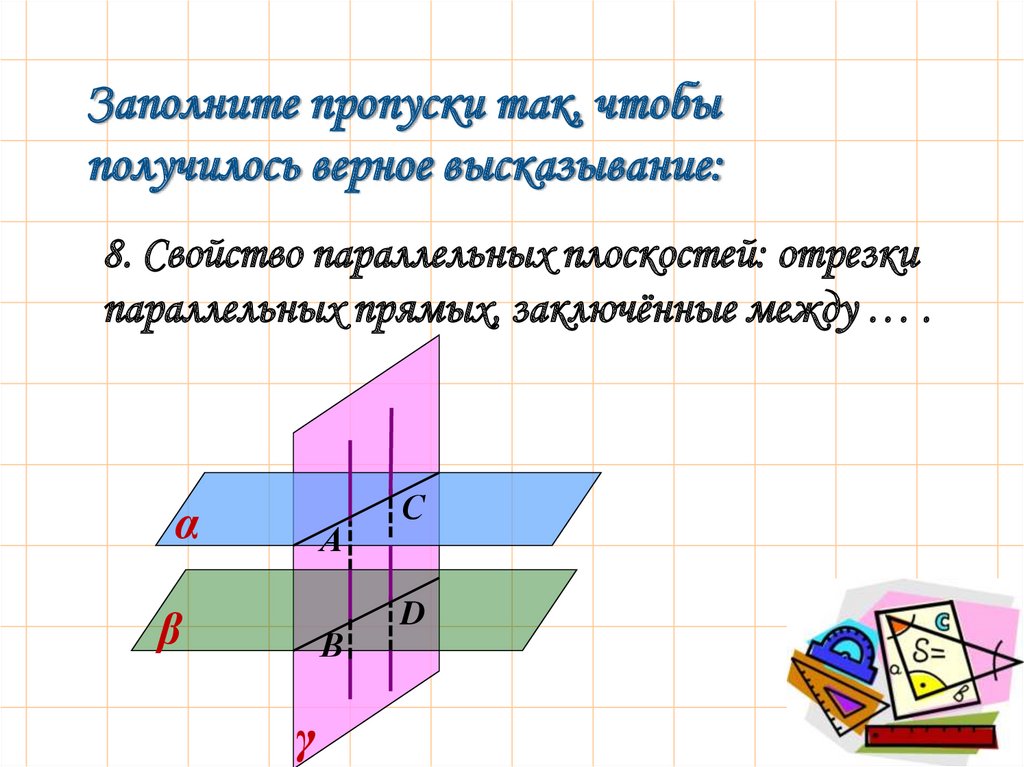
Заполните пропуски так, чтобыполучилось верное высказывание:
8. Свойство параллельных плоскостей: отрезки
параллельных прямых, заключённые между … .
α
А
β
В
γ
С
D
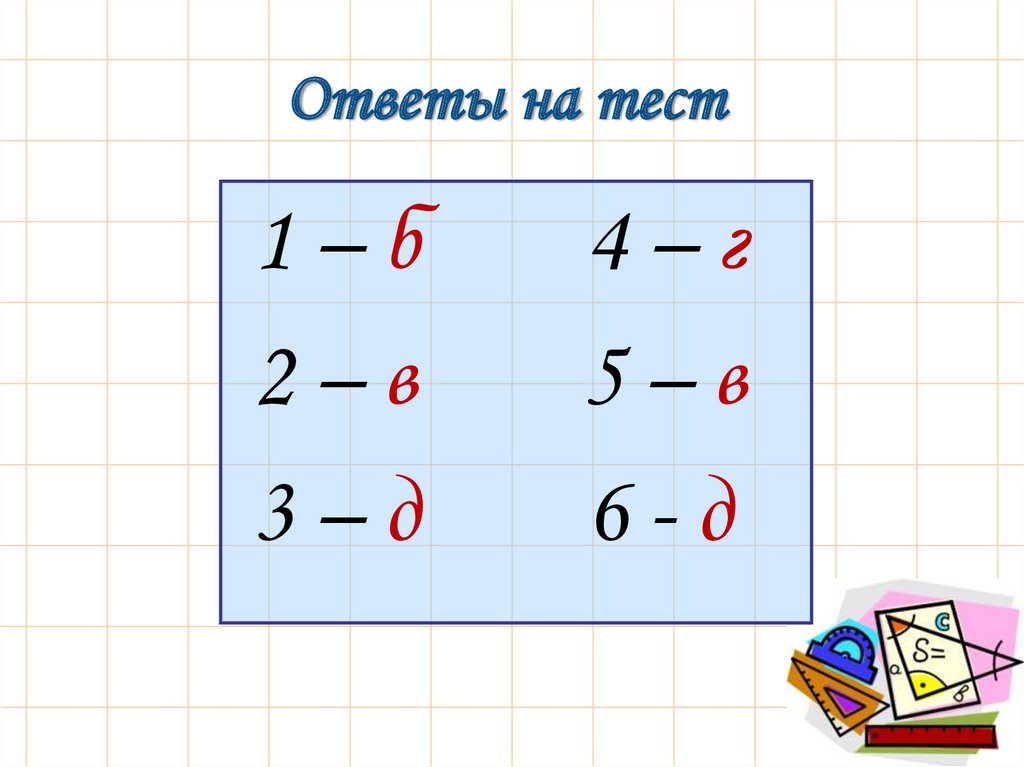
14. Ответы на тест
1–б2–в
3–д
4–г
5–в
6-д
15.
Задача № 1.Через точку О, лежащую между параллельными
плоскостями α и β, проведены прямые l и m.
Прямая l пересекает плоскости α и β в точках
D1 и D2 соответственно, прямая m - в точках
С1 и С2. Найдите длину отрезка D1D2 , если
D1О = 6 см, С2D2 : С1D1 = 2 : 3.
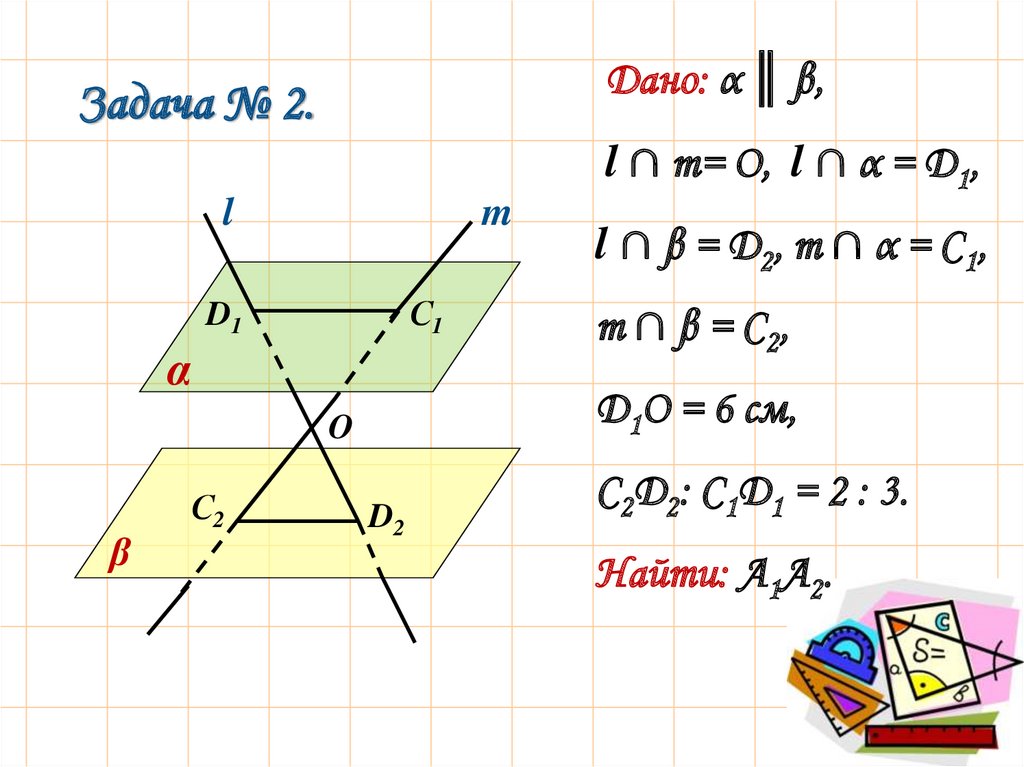
16.
Дано: α ║ β,Задача № 2.
l ∩ m= O, l ∩ α = D1,
l
m
С1
D1
α
β
m ∩ β = С 2,
D1О = 6 см,
O
С2
l ∩ β = D 2, m ∩ α = С 1,
D2
С2D2: С1D1 = 2 : 3.
Найти: А1А2.
17.
Задача № 2.Дан тетраэдр ABCD.
а) Построить плоскость тетраэдра EFP,
проходящую через середины рёбер AB, AC и AD.
б) Доказать, что плоскость EFP параллельна
плоскости BCD.
в) Доказать, что треугольник EFP подобен
треугольнику BCD.
г) Найти площадь треугольника EFP, если
площадь треугольника BCD равна 36 см2.





 Математика
Математика








