Circuite numerice - A Electronică digital - C Note de curs

1. Circuite numerice - A Electronică digital - C Note de curs

Universitatea din Petroșani
Departamentul Automatică, Calculatoare, Inginerie Electrică și Energetică
Circuite numerice
Electronică digital
-
A
C
Note de curs
Conf.univ.dr.ing. Nicolae PĂTRĂȘCOIU

2.

Bibliografie
1. Baluta Gh.,
Circuite numerice, Editura Matrix Rom, Bucuresti, 1999
2. Blakeslee Th. R.,
Proiectarea cu circuite logice MSI si LSI standard.
Editura Tehnica, Bucuresti,1998
3. Festila L,
Electronica digitala,
Universitatea Tehnica , Cluj –Napoca, 1994
4. Muresan T.,.
Gontean A
Circuite integrate numerice
Editura de Vest, Timisoara, 1996
5. Groza V.
Analiza si sinteza dispozitivelor numerice
Universitatea Tehnica, Timisoara, 2004
6.Poanta A
Patrascoiu N.
Circuite si echipamente electronice in industrie
Editura Stiintifica si Enciclopedica, Bucuresti, 1997
7.Poanta A
Dispozitive si circuite electronice vol.I, vol II
Universitatea din Petrosani, 1997
8.Patrascoiu N.
Poanta A
Circuite numerice/Electronică digitală
logica Note de curs, Universitatea din Petrosani, 2015,
format digital
https://upet.academia.edu/Patrascoiu/Teaching-Documents

3. CIRCUITE COMBINAȚIONALE COMPLEXE

Convertoare de cod: realizează conversia dintr-un cod binar în alt
cod binar - conversia din cod binar în cod Gray si invers.
Codificatoare
Codificatoare propriu-zise: generează la ieșire un cod care permite
identificarea intrării active la un moment dat, funcționarea presupune
ca, în orice moment, să nu fie mai mult de o intrare activă.
Codificatoare cu prioritate: CLC care generează la ieșire un cod
corespunzător intrării cu prioritatea cea mai mare, activă în acel moment
Demultiplexoare: CLC care realizează transferul informației de pe
o intrare unică pe una dintre mai multe ieșiri, aceasta fiind selectată
printr-un cod numit cuvânt de adresă.
Decodificatoare
Decodificatoare binare: CLC care identifică, prin activarea unei
ieșiri, toate codurile posibile generate la intrările acestuia.
Decodificatoarele BCD: decodificatoare de 4 biți având 10 ieșiri
Decodificatoare BCD – 7 segmente: destinate pentru comanda
display-urilor la care afișarea cifrelor sistemului zecimal de
numerație se poate face prin activarea segmentelor acestuia,
realizate cu LED sau LCD

4. CIRCUITE COMBINAȚIONALE COMPLEXE

1.1. Multiplexoare (MUX)
1.1.1.Definiţii. Principii de realizare.
CLC complexe care realizează operaţia de multiplexare, operaţia ce constă în transferul
informaţiei de pe mai multe intrări I0, I1,…, In-1 pe o singură ieşire, y.
funcţia realizată de
circuit va fi de forma:
y An 1 An 2
A1 A0 I0 An 1 An 2
An 1 An 2
A1 A0 I1 An 1 An 2
A1 A0 I 2
A1 A0 I 2n 1
Funcţia poate fi reprezentată dintr-o formă
restrânsă având în vedere constituenţii unităţii:
2 n 1
y
P I
i
i 0
i

5. CIRCUITE COMBINAȚIONALE COMPLEXE

1.1. Multiplexoare (MUX)
1.1.1.Definiţii. Principii de realizare.
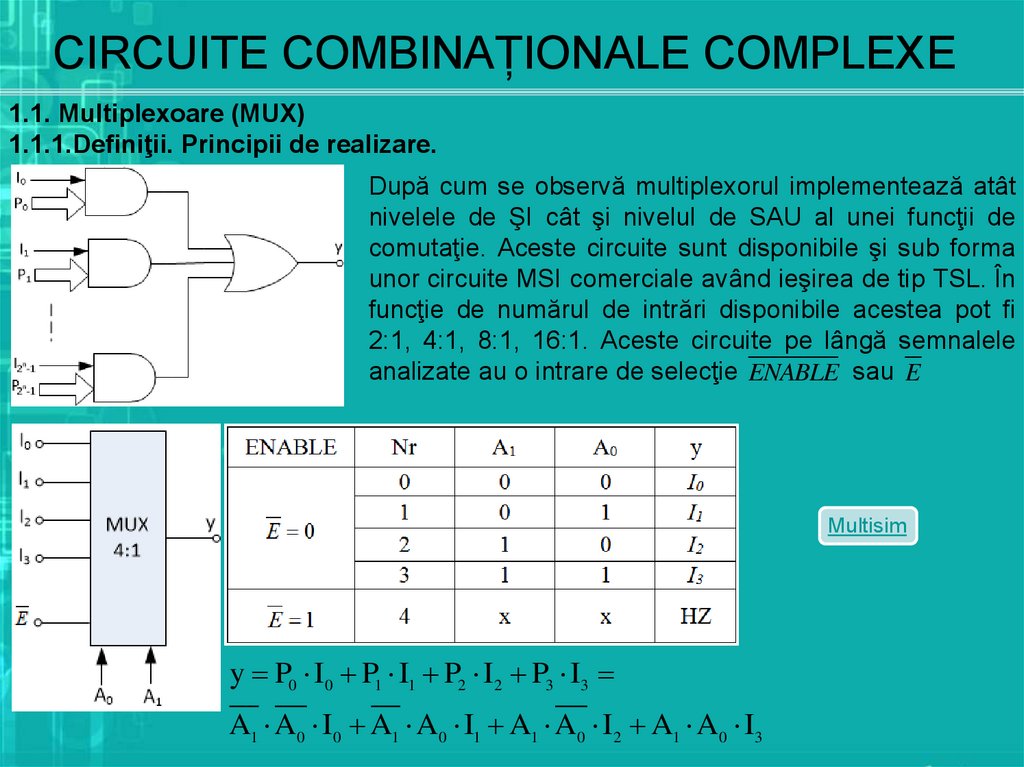
După cum se observă multiplexorul implementează atât
nivelele de ŞI cât şi nivelul de SAU al unei funcţii de
comutaţie. Aceste circuite sunt disponibile şi sub forma
unor circuite MSI comerciale având ieşirea de tip TSL. În
funcţie de numărul de intrări disponibile acestea pot fi
2:1, 4:1, 8:1, 16:1. Aceste circuite pe lângă semnalele
analizate au o intrare de selecţie ENABLE sau E
Multisim
y P0 I0 P1 I1 P2 I2 P3 I3
A1 A0 I0 A1 A0 I1 A1 A0 I2 A1 A0 I3

6. CIRCUITE COMBINAȚIONALE COMPLEXE

1.1. Multiplexoare (MUX)
1.1.2. Extinderea capacitaţii multiplexoarelor
Extinderea multiplexării de la mai multe intrări la o ieşire, se poate realiza pe două căi:
1. utilizând numai multiplexoare
2. utilizând multiplexoare şi decodificatoare.
Ambele metode pornesc de la împărţirea în câmpuri a cuvântului de selecție.
Cuvântul de adresă
se împarte în două
câmpuri și fiecare se
repartizează
unui
nivel.
Câmpul cu biţii cei
mai semnificativi se
repartizează ultimului
nivel care conţine
doar un MUX, iar
câmpul cu biţii cei
mai
puţin
semnificativi la primul
nivel.
Multisim
Multisim

7. CIRCUITE COMBINAȚIONALE COMPLEXE

1.1. Multiplexoare (MUX)
1.1.2. Extinderea capacitaţii multiplexoarelor
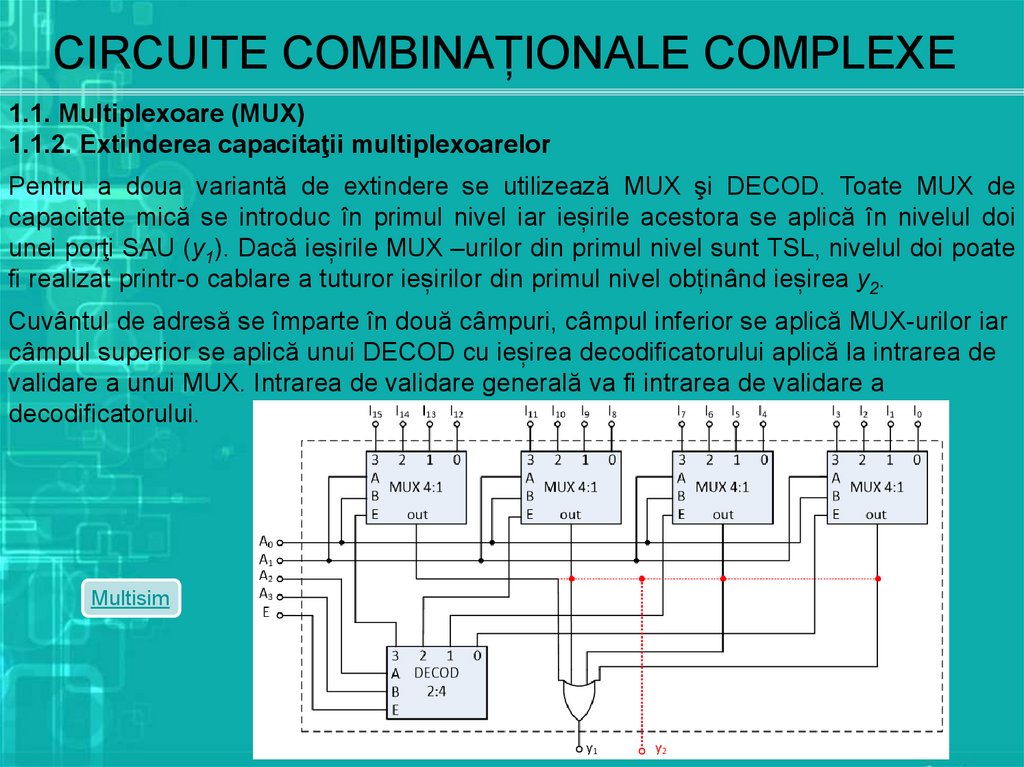
Pentru a doua variantă de extindere se utilizează MUX şi DECOD. Toate MUX de
capacitate mică se introduc în primul nivel iar ieșirile acestora se aplică în nivelul doi
unei porţi SAU (y1). Dacă ieșirile MUX –urilor din primul nivel sunt TSL, nivelul doi poate
fi realizat printr-o cablare a tuturor ieșirilor din primul nivel obținând ieșirea y2.
Cuvântul de adresă se împarte în două câmpuri, câmpul inferior se aplică MUX-urilor iar
câmpul superior se aplică unui DECOD cu ieșirea decodificatorului aplică la intrarea de
validare a unui MUX. Intrarea de validare generală va fi intrarea de validare a
decodificatorului.
Multisim

8. CIRCUITE COMBINAȚIONALE COMPLEXE

1.1. Multiplexoare (MUX)
1.1.3. Aplicaţiile MUX în implementarea funcţiilor de comutație
MUX implementează atât nivelul de ŞI cât şi nivelul de SAU astfel că acesta poate fi
utilizat pentru implementarea funcţiilor logice.
Pe intrările MUX se aplică valorile αi din tabela de adevăr iar variabilele sunt
reprezentate de variabilele de selectare (adresele MUX) astfel că având n adrese poate
fi implementată orice funcţie logică de n variabile dată în forma FCD.
Un MUX 2n :1 reprezintă un modul logic universal de ordinul n, ULMn (Universal Logic
Module) și implementarea funcțiilor de comutație este posibilă deoarece:
f ui fi ui fi
0
1
0
fi f(ui 0)
unde
1
fi f(ui 1)
În acest caz coeficienţii αi {0, 1, ui , ui}
Un MUX 2:1 poate fi utilizat pentru orice funcţie de două variabile (operaţie logică) în
funcţie de valorile posibile αi={0, 1, u0, u0} aplicate la intrările acestuia
Pe intrarea de adresă A se
aplică variabila u1, iar pe
intrările
I0,I1
toate
combinaţiile
posibile
pentru αi={0, 1, u0, u0}.

9. CIRCUITE COMBINAȚIONALE COMPLEXE

1.1. Multiplexoare (MUX)
1.1.3. Aplicaţiile MUX în implementarea funcţiilor de comutație
Operaţia rezultă din funcţia realizată de MUX va fi dată în expresia:
De exemplu pentru α0=α1=0 se obţine: y u 0 u1 0 0
y u 1 α0 u1 α1
În mod similar se obţin şi celelalte operaţii menţionate în tabelul anterior
Soluţiile de implementare a funcţiilor de comutaţie sunt diversificate deoarece MUX de
capacitate mai mare se pot obține din MUX de capacitate mai mică pe mai multe nivele.
Fiecare soluţie utilizează un anumit tip de circuite MUX, un număr diferit de circuite, cu
adâncimi diferite şi complexitate diferită.
O funcţie de trei variabile poate fi
implementată conform celor analizate
printr-un MUX 8:1 sau orice altă
configuraţie care permite obţinerea
unui MUX 8:1 utilizând MUX-uri de
capacitate mai mică: MUX 2:1, MUX
4:1 sau combinaţii ale acestora.

10. CIRCUITE COMBINAȚIONALE COMPLEXE

1.1. Multiplexoare (MUX)
1.1.3. Aplicaţiile MUX în implementarea funcţiilor de comutație
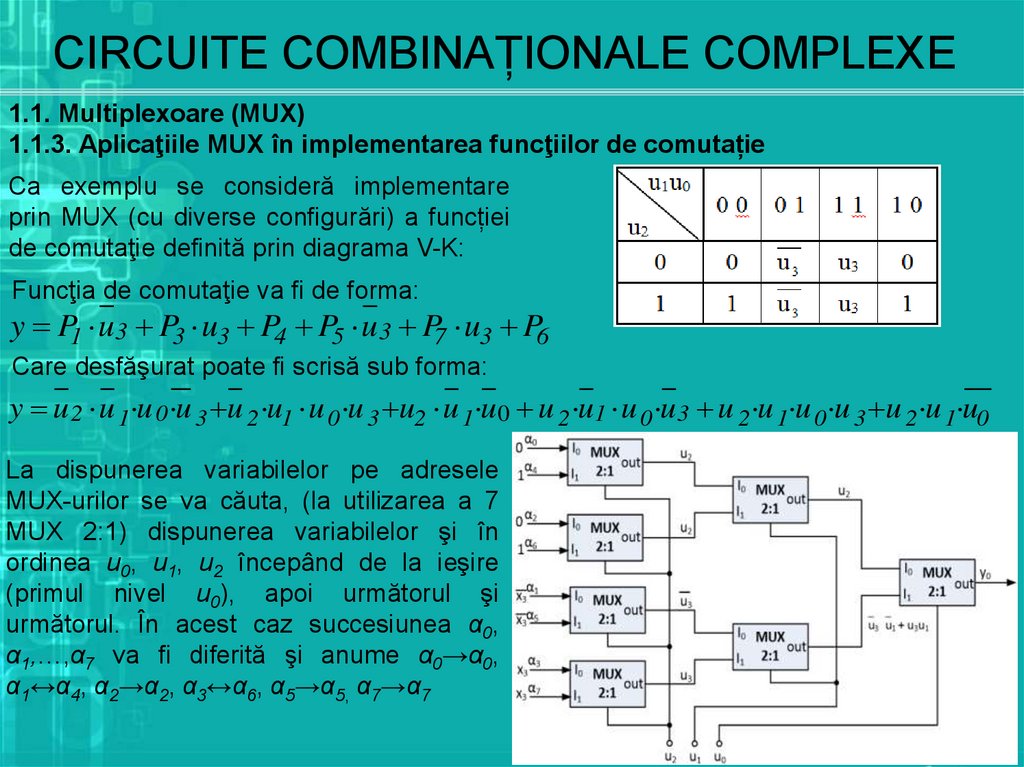
Ca exemplu se consideră implementare
prin MUX (cu diverse configurări) a funcției
de comutaţie definită prin diagrama V-K:
Funcţia de comutaţie va fi de forma:
y P1 u3 P3 u3 P4 P5 u 3 P7 u3 P6
Care desfăşurat poate fi scrisă sub forma:
y u 2 u 1 u 0 u 3 u 2 u1 u 0 u 3 u2 u 1 u 0 u 2 u1 u 0 u 3 u 2 u 1 u 0 u 3 u 2 u 1 u0
La dispunerea variabilelor pe adresele
MUX-urilor se va căuta, (la utilizarea a 7
MUX 2:1) dispunerea variabilelor şi în
ordinea u0, u1, u2 începând de la ieşire
(primul nivel u0), apoi următorul şi
următorul. În acest caz succesiunea α0,
α1,…,α7 va fi diferită şi anume α0→α0,
α1↔α4, α2→α2, α3↔α6, α5→α5, α7→α7

11. CIRCUITE COMBINAȚIONALE COMPLEXE

1.1. Multiplexoare (MUX)
1.1.3. Aplicaţiile MUX în implementarea funcţiilor de
comutație

12. CIRCUITE COMBINAȚIONALE COMPLEXE

1.1. Multiplexoare (MUX)
1.1.3. Aplicaţiile MUX în implementarea funcţiilor de comutație
Multisim

13. CIRCUITE COMBINAȚIONALE COMPLEXE

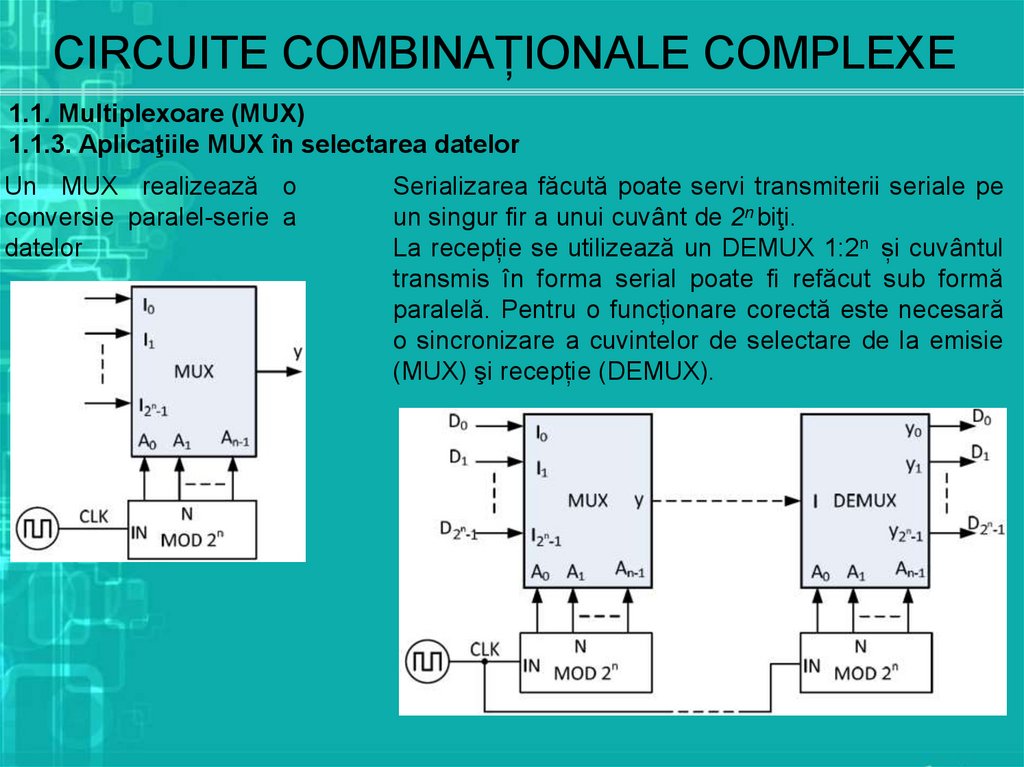
1.1. Multiplexoare (MUX)
1.1.3. Aplicaţiile MUX în selectarea datelor
Un MUX realizează o
conversie paralel-serie a
datelor
Serializarea făcută poate servi transmiterii seriale pe
un singur fir a unui cuvânt de 2n biţi.
La recepție se utilizează un DEMUX 1:2n și cuvântul
transmis în forma serial poate fi refăcut sub formă
paralelă. Pentru o funcționare corectă este necesară
o sincronizare a cuvintelor de selectare de la emisie
(MUX) şi recepție (DEMUX).

14. CIRCUITE COMBINAȚIONALE COMPLEXE

1.2.Comparatoare
1.2.1. Definiţii. Principii de realizare
Comparatoarele realizează compararea a două coduri de unu,
doi, sau mai mulţi biţi. Comparatoarele conţin intrările aferente
celor două numere A şi B (fiecare având unu, doi sau mai mulţi
biţi) şi cele 3 ieşiri (A < B, A = B, A > B) la care se obţine
rezultatul comparaţiei.
Comparatorul de 1 bit
are două intrări A0 şi B0
fiecare de un bit şi trei
ieşiri (A < B, A = B, A >
B)
Pot fi scrise funcţiile logice (de comutaţie) pentru cele trei ieşiri și realiza schema logică:
Multisim

15. CIRCUITE COMBINAȚIONALE COMPLEXE

1.2.Comparatoare
1.1.2. Comparatoare de doi sau mai mulţi biţi
Pentru a deduce structura se va
avea în vedere că numerele A şi
B pot fi descrise prin expresiile:
Dacă procesul de comparaţie începe cu cei mai semnificativi biţi tabela de adevăr este:
Se observă că pentru compararea
celor mai semnificativi biţi rezultă
funcţiile de la comparatorul de un
bit. Pentru biţii cei mai puţini
semnificativi A0,B0, în cazurile de
inegalitate se introduce suplimentar
la intrări funcția f(A1=B1)
Multisim

16. CIRCUITE COMBINAȚIONALE COMPLEXE

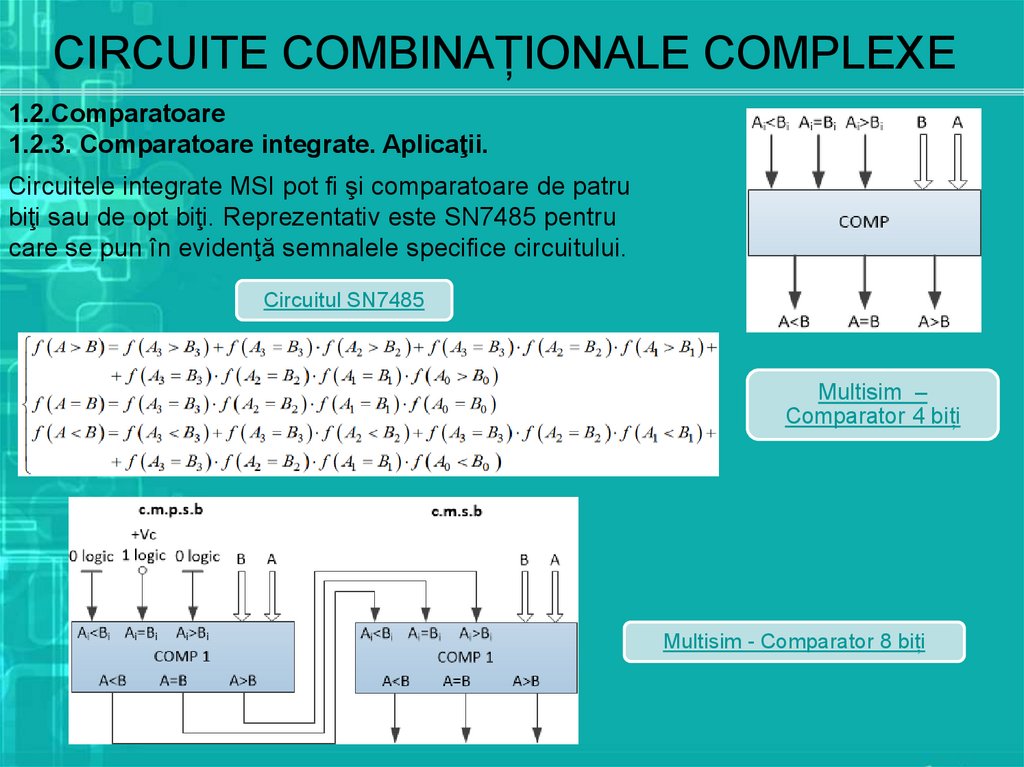
1.2.Comparatoare
1.2.3. Comparatoare integrate. Aplicaţii.
Circuitele integrate MSI pot fi şi comparatoare de patru
biţi sau de opt biţi. Reprezentativ este SN7485 pentru
care se pun în evidenţă semnalele specifice circuitului.
Circuitul SN7485
Multisim –
Comparator 4 biți
Multisim - Comparator 8 biți

17. CIRCUITE COMBINAȚIONALE COMPLEXE

1.2.Comparatoare
1.2.3. Comparatoare integrate. Aplicaţii.
Comparatorul poate fi utilizat ca un decodificator de adresă. Utilizat în tandem cu un
decodificator comparatorul poate extinde decodificarea la un spaţiu mai mare de adrese,
numărul circuitelor fiind mai redus faţă de cazul când se utilizează numai
decodificatoare.
Pentru un decodificator de adresă de opt biţi, A0÷A7,
poate fi utilizat cu un comparator de opt biţi (74LS682)
cu intrările Pi,Qi (i=0,1,....7), care are ieşirile active pe 0
LOGIC. Pe intrările Qi se aplică adresele A0,A1,...A7, iar
intrările Pi sunt utilizate pentru a stabili adresa
selectată.
Multisim

18. CIRCUITE COMBINAȚIONALE COMPLEXE

1.2.Comparatoare
1.2.3. Comparatoare integrate. Aplicaţii.
Extensia numărului de adrese decodificate, precum şi a adreselor selectate poate fi
realizată printru-un comparator şi un decodificator. Pentru a extinde numărul adreselor la
unsprezece A0, A1, ..A10 poate fi utilizat un comparator de opt biţi şi un decodificator de
trei biţi. Adresele selectate se stabilesc în funcţie de modul de repartizare a adreselor ce
urmează a fi decodificate la intrările celor două circuite

19. CIRCUITE COMBINAȚIONALE COMPLEXE

1.3.Generatoare (detectoare de paritate / imparitate ).
1.3.1.Principii de realizare.
Definire: CLC utilizate pentru verificarea corectitudinii în cazul transmisiei la distanţă,
prin diferite canale, a informaţiei numerice. La codul transmis se adaugă bitul P/I
1 logic dacă numărul biților din cod este par
P/I =
0 logic dacă numărul biților din cod este impar P/I → bit de paritate
P/I =
1 logic dacă numărul biților din cod este impar
0 logic dacă numărul biților din cod este par
P/I → bit de imparitate
La emisie bitul P/I se sintetizează printr-un circuit
generator de paritate/imparitate, iar la recepţie
prin acelaşi circuit care, va fi denumit detector de
paritate/imparitate.
Exemplu generator/detector de paritate/imparitate de doi biţi:
Multisim
P/I
Poarta 2 din configurația generatorului/detectorului de paritate/imparitate este utilizată
doar pentru selecţia tipului de control.

20. CIRCUITE COMBINAȚIONALE COMPLEXE

1.3.Generatoare (detectoare de paritate / imparitate ).
1.3.1.Principii de realizare.
se observă că o intrare cu valori 1 sau 0
(P/I) poate fi utilizată pentru selecția
Din relația:
tipului de paritate/imparitate astfel:
pentru 1 LOGIC → generator/detector de paritate (YP),
Multisim
pentru 0 LOGIC → generator/detector de imparitate (YI).
Sinteza
unui
generator/detector
de
paritate/imparitate de 3, 4 sau mai mulţi biţi
poate fi realizată similar. Pentru un circuit de
patru biţi se va obţine configuraţia:
Pentru transmiterea informației la cod se adaugă bitul P/I astfel că pentru un cuvânt de
date de doi biţi este necesar la emisie un generator P/I de minim trei biţi:
La emisie, la biţi de date se ataşează bitul P/I și se
transmite un cuvânt de trei biţi, doi de date şi bitul P/I.
Multisim

21. CIRCUITE COMBINAȚIONALE COMPLEXE

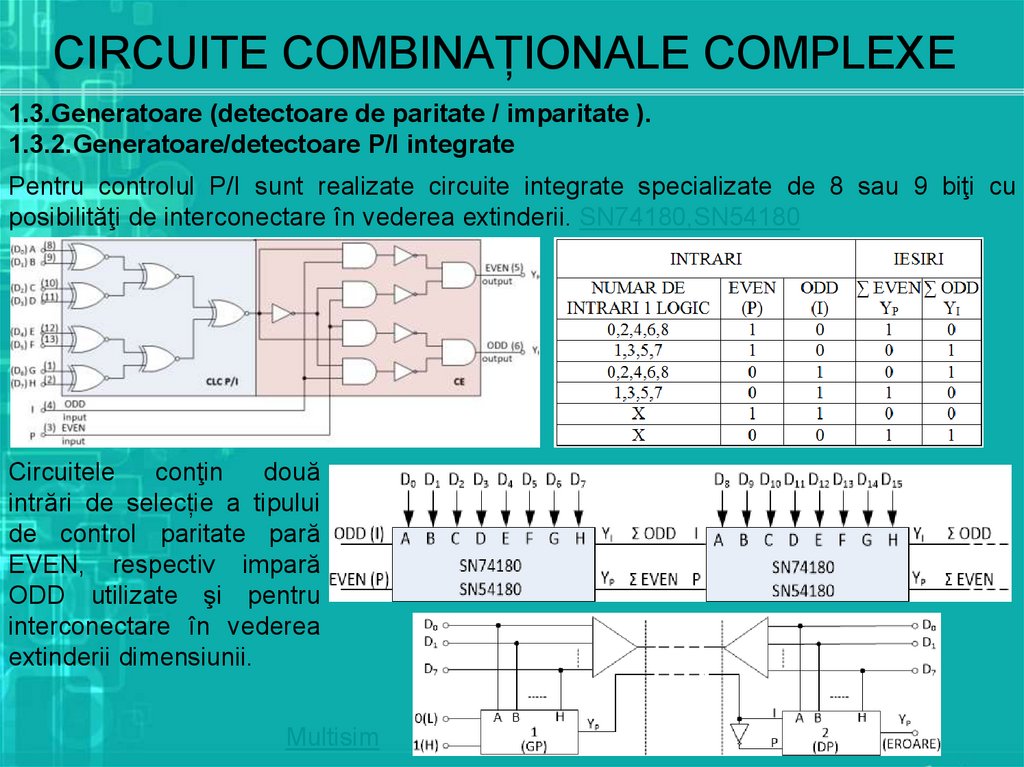
1.3.Generatoare (detectoare de paritate / imparitate ).
1.3.2.Generatoare/detectoare P/I integrate
Pentru controlul P/I sunt realizate circuite integrate specializate de 8 sau 9 biţi cu
posibilităţi de interconectare în vederea extinderii. SN74180,SN54180
Circuitele
conţin
două
intrări de selecție a tipului
de control paritate pară
EVEN, respectiv impară
ODD utilizate şi pentru
interconectare în vederea
extinderii dimensiunii.
Multisim

22. CIRCUITE COMBINAȚIONALE COMPLEXE

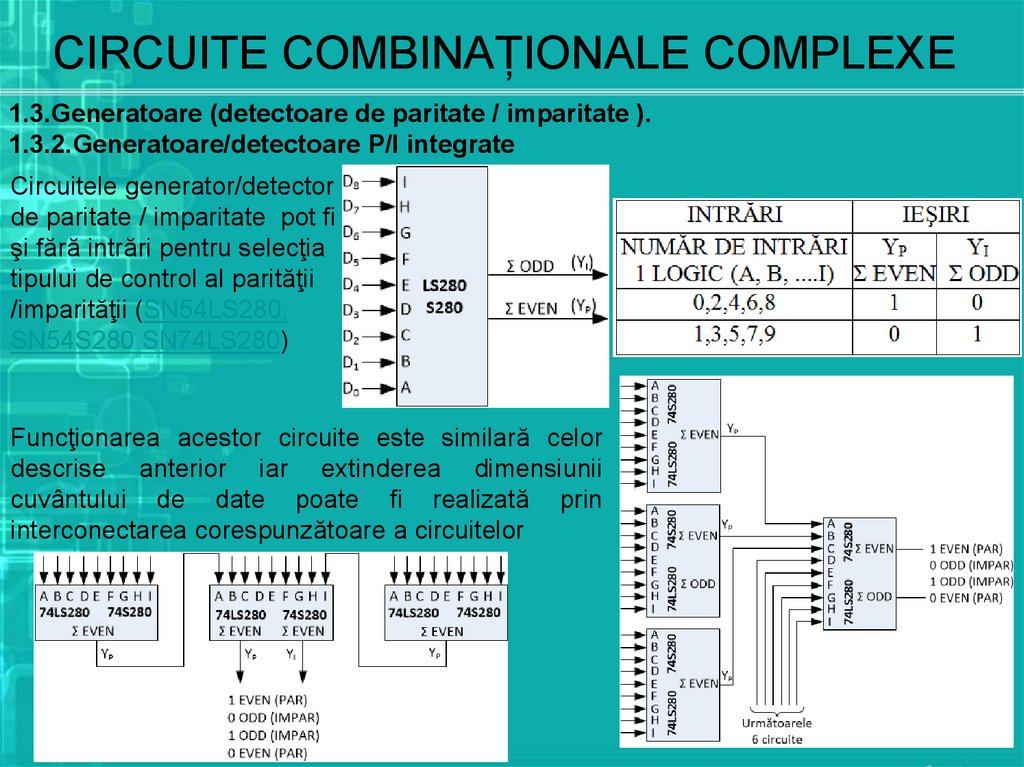
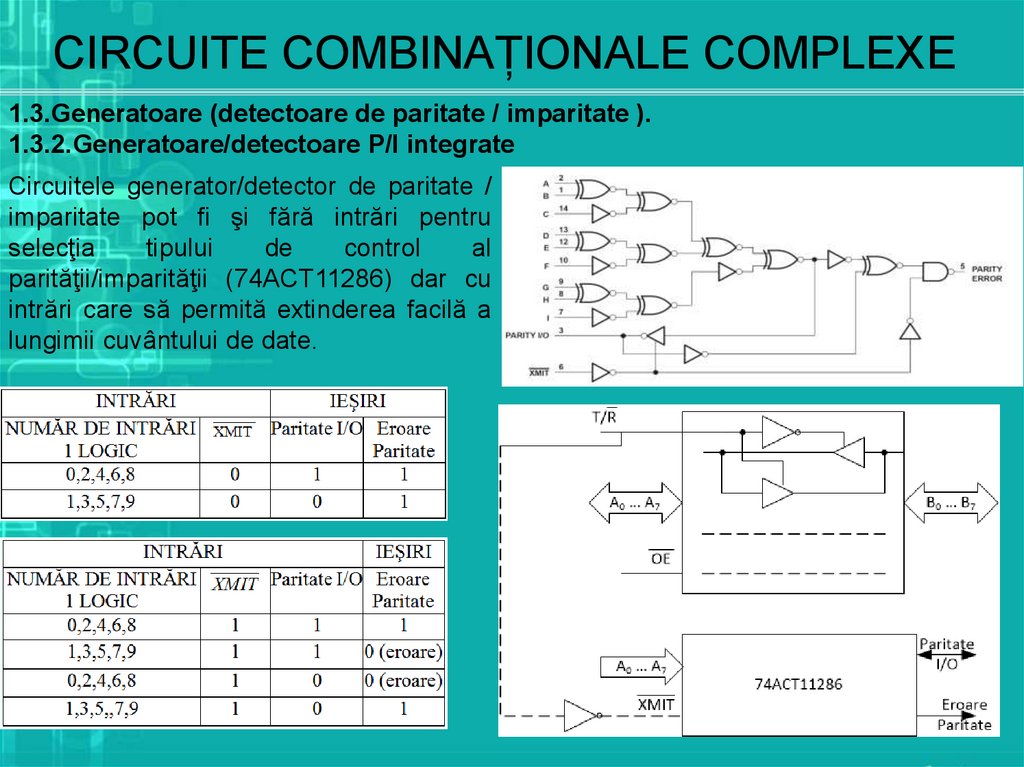
1.3.Generatoare (detectoare de paritate / imparitate ).
1.3.2.Generatoare/detectoare P/I integrate
Circuitele generator/detector
de paritate / imparitate pot fi
şi fără intrări pentru selecţia
tipului de control al parităţii
/imparităţii (SN54LS280,
SN54S280 SN74LS280)
Funcţionarea acestor circuite este similară celor
descrise anterior iar extinderea dimensiunii
cuvântului de date poate fi realizată prin
interconectarea corespunzătoare a circuitelor

23. CIRCUITE COMBINAȚIONALE COMPLEXE

1.3.Generatoare (detectoare de paritate / imparitate ).
1.3.2.Generatoare/detectoare P/I integrate
Circuitele generator/detector de paritate /
imparitate pot fi şi fără intrări pentru
selecţia
tipului
de
control
al
parităţii/imparităţii (74ACT11286) dar cu
intrări care să permită extinderea facilă a
lungimii cuvântului de date.

24. CIRCUITE COMBINAȚIONALE COMPLEXE

1.4. Sumatoare
Sumatoarele circuite logice combinaţionale care realizează operaţia de însumare.
Pentru a
structura
circuit
sumatorul
bit
Si Ai Bi
pune în evidenţă
unui astfel de
se
consideră
elementar de un
T1 1 Ai Bi
Si Ai Bi Ti Ai Bi Ti Ai Bi Ti Ai Bi Ti
Si Ai Bi Ti Bi Ti Ai Bi Ti Bi Ti
Si Ai Bi Ti Ai Bi Ti
Si Ai Bi Ti
Ti 1 Ai Bi Ti Ai Bi Ti Ai Bi Ti Ai Bi T
Ti 1 Ai Bi Ti Bi Ti Bi Ti Ai Bi Ti Bi Ti
Multisim

25. CIRCUITE COMBINAȚIONALE COMPLEXE

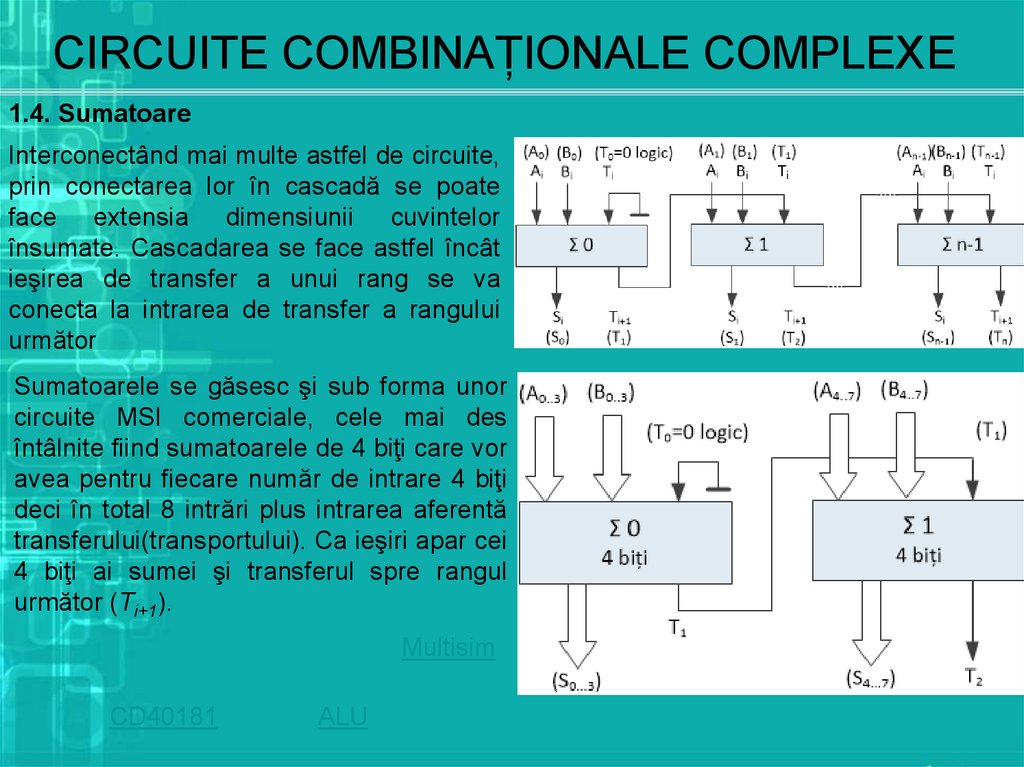
1.4. Sumatoare
Interconectând mai multe astfel de circuite,
prin conectarea lor în cascadă se poate
face extensia dimensiunii cuvintelor
însumate. Cascadarea se face astfel încât
ieşirea de transfer a unui rang se va
conecta la intrarea de transfer a rangului
următor
Sumatoarele se găsesc şi sub forma unor
circuite MSI comerciale, cele mai des
întâlnite fiind sumatoarele de 4 biţi care vor
avea pentru fiecare număr de intrare 4 biţi
deci în total 8 intrări plus intrarea aferentă
transferului(transportului). Ca ieşiri apar cei
4 biţi ai sumei şi transferul spre rangul
următor (Ti+1).
Multisim
CD40181
ALU

26. CIRCUITE COMBINAȚIONALE COMPLEXE

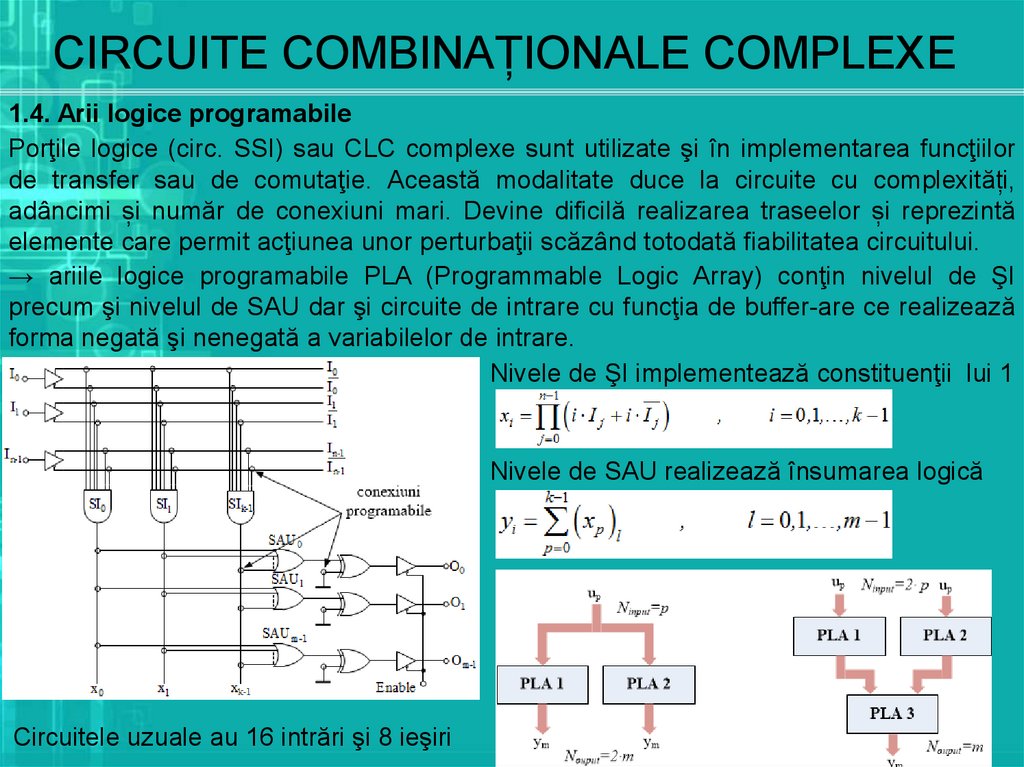
1.4. Arii logice programabile
Porţile logice (circ. SSI) sau CLC complexe sunt utilizate şi în implementarea funcţiilor
de transfer sau de comutaţie. Această modalitate duce la circuite cu complexități,
adâncimi și număr de conexiuni mari. Devine dificilă realizarea traseelor și reprezintă
elemente care permit acţiunea unor perturbaţii scăzând totodată fiabilitatea circuitului.
→ ariile logice programabile PLA (Programmable Logic Array) conţin nivelul de ŞI
precum şi nivelul de SAU dar şi circuite de intrare cu funcţia de buffer-are ce realizează
forma negată şi nenegată a variabilelor de intrare.
Nivele de ŞI implementează constituenţii lui 1
Nivele de SAU realizează însumarea logică
Circuitele uzuale au 16 intrări şi 8 ieşiri

27. CIRCUITE COMBINAȚIONALE COMPLEXE

1.5. Circuite cu funcţii selectabile
Sunt CLC care pot genera la ieşiri mai multe funcţii pentru aceeaşi intrare sau aceleaşi
intrări și aceste funcţii pot fi selectate în raport cu un cuvânt de comandă.
Se consideră circuitul “unu – complementează – trece
– zero”, UCTZ
Funcţiile pot fi selectate prin intermediul unui cuvânt de
comandă cu lungimea n log 2 4 log 2 22 2
Problema sintezei circuitului constă în alegerea acelor variante de asignare a codului de
comandă la cele 4 funcţii aşa încât să se obţină o implementare optimă a circuitului.
În cazul implementării cu circuite MSI alegerea codurilor de comandă se face aşa încât
în diagrama V - K intrarea apare ca variabilă reziduu plasată în diagonala tabelei.
Multisim

28. CIRCUITE COMBINAȚIONALE COMPLEXE

1.5. Circuite cu funcţii selectabile
Dacă se analizează cele două tipuri de implementări se constată că diferă doar numărul
de porţi necesare pentru implementare.
Dacă variabila reziduu se plasează pe aceeaşi linie (sau coloană) un termen va conţine
3 variabile deoarece între forma negată şi nenegată a variabilei reziduu nu se poate
stabilită o adiacenţă
UCTZ
Reprezentativ în această categorie este circuitul 74181
care este o ALU de 4 biţi cu două grupuri de intrări Ai, Bi de
4 biţi, o intrare de transport Ti de la rangul anterior şi o
ieşire de transport Ti+4 către rangul următor.
M = 0 , operaţii aritmetice;
M = 1 , operaţii logice.
74LS181
Multisim

29. CIRCUITE COMBINAȚIONALE COMPLEXE

1.6 Hazardul în CLC
1.6.1. Definiţii. Clasificări.
Pentru implementarea funcţiilor de comutaţie utilizator are la dispoziţie soluţii multiple
care trebuie să asigure o funcţionare corectă a cu o structură hardware minimală. În
determinarea funcțiilor de comutaţie pe baza algebrei booleene nu se ține seama de
variabila timp și se consideră timpii de propagare tp = 0
În realitate însă tp ≠ 0 şi de asemenea pe traseele de legătură pot apărea întârzieri. În
perioadele tranzitorii, proprietatea de noncontradicţie şi terţ exclus nu se mai verifică și
datorită acestor erori de funcţionare apare o funcţionare aleatoare cunoscută şi sub
denumirea de hazard.
Hazardul în CLC este determinat de doi factori:
comutaţia asincronă a variabilelor de intrare;
propagarea semnalelor spre intrările unei porţi pe trasee cu timpi de întârziere diferiţi.
În raport cu forma de manifestare, hazardul poate fi împărţit în trei categorii:
hazard static;
hazard dinamic;
hazard funcţional.

30. CIRCUITE COMBINAȚIONALE COMPLEXE

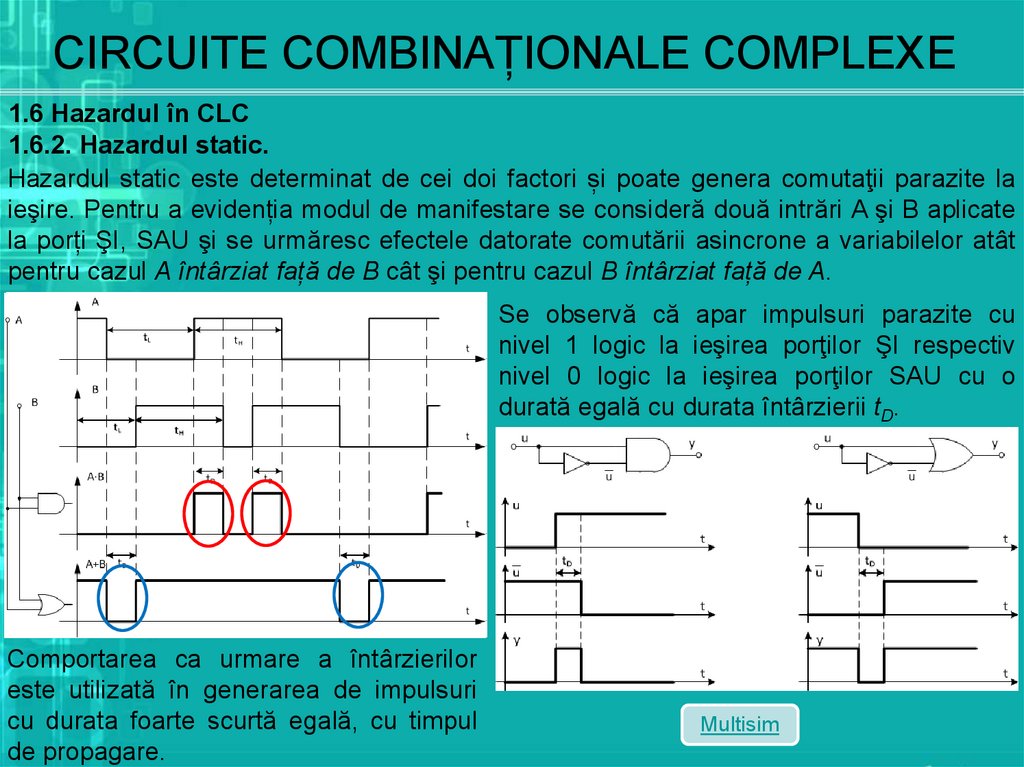
1.6 Hazardul în CLC
1.6.2. Hazardul static.
Hazardul static este determinat de cei doi factori și poate genera comutaţii parazite la
ieşire. Pentru a evidenția modul de manifestare se consideră două intrări A şi B aplicate
la porți ŞI, SAU şi se urmăresc efectele datorate comutării asincrone a variabilelor atât
pentru cazul A întârziat față de B cât şi pentru cazul B întârziat față de A.
Se observă că apar impulsuri parazite cu
nivel 1 logic la ieşirea porţilor ŞI respectiv
nivel 0 logic la ieşirea porţilor SAU cu o
durată egală cu durata întârzierii tD.
Comportarea ca urmare a întârzierilor
este utilizată în generarea de impulsuri
cu durata foarte scurtă egală, cu timpul
de propagare.
Multisim

31. CIRCUITE COMBINAȚIONALE COMPLEXE

1.6 Hazardul în CLC
1.6.3. Identificarea şi eliminarea hazardului static
Hazardul static poate apărea în funcţionarea unor CLC atunci când funcţia de comutaţie,
exprimată sub formă disjunctivă, poate fi adusă la o expresie de forma:
sau
pentru anumite valori ale variabilelor uj astfel încât:
Se consideră exemplu unu CLC cu 3 intrări descris de următoarea funcție de comutație:
se
urmărește
identificarea
condițiilor
de apariție a
hazardului în cazul comutării
unei singure variabile de intrare
prin verificarea condițiilor
Deoarece în această verificare nu se regăsesc formele se concluzionează faptul că
această funcţie nu conduce la hazard static la comutarea unei singure variabile
implementată sub forma dată.

32. CIRCUITE COMBINAȚIONALE COMPLEXE

1.6 Hazardul în CLC
1.6.3. Identificarea şi eliminarea hazardului static
Considerând o
având schema logică
funcţie de forma:
Se observă că
va putea genera hazard
Generarea hazardului poate fi pusă în evidenţă și în diagrama de semnal aferentă
Dacă u3=u2=1 la comutarea din 1 în 0 a intrării u1,
ieşirea va deveni 0 pe durata tD a timpului de
propagare pe poartă → funcţionare defectuoasă.
Din diagrama V – K:
Funcţia va deveni:
Cu schema logică:
Se constată că, această funcţionare determină trecerea din
u1 u3
suprafaţă unui implicant IP
în suprafaţa unui alt
implicant IP u1 u2 între care distanţa de cod este egală cu 1.
Eliminarea hazardului poate fi realizată prin deplasarea
funcţionării în interiorul suprafeţei aceluiaşi implicant prim și
se va considera implicatul prim neesenţial u2 u3
Multisim

33. CIRCUITE COMBINAȚIONALE COMPLEXE

1.6 Hazardul în CLC
1.6.3. Identificarea şi eliminarea hazardului static
având schema
Considerând o
logică
funcţie de forma:
Se observă că pentru u2 = u3 = 0 rezultă F u1 ,0, 0 u1 u1 și va putea genera hazard
Analizând configuraţia de implementare şi diagrama de semnal pot fi stabilite situaţiile în
care se produce hazardul
Dacă u =u = 0 la comutarea din 0 în 1 a intrării u ,
3
2
1
ieşirea va deveni 1 pe durata tD a timpului de
propagare pe poartă → funcţionare defectuoasă.
Din diagrama V – K:
Eliminarea hazardului poate fi
realizată prin considerarea unui
implicatul prim neesenţial
Se constată și în acest caz că, această funcţionare
determină trecerea de la un implicant IP la un alt
implicant IP cu distanţa de cod este egală cu 0.
Rezultă următoarea funcţie de comutaţie:
căreia îi corespunde
schema logică
Multisim

34. CIRCUITE LOGICE SECVENȚIALE (CLS)

2.1. Structură. Definiţii. Clasificări.
Circuitele logice secvenţiale (CLS) pot fi definite prin completare pornind de la CLC și
poate fi definit ca fiind un CLC la care apare o reacţie și în funcţionarea căruia se ia în
considerare variabila timp. Structura unui CLS va putea fi reprezentată conform figurii:
Variabilele u1, u2,...,up reprezintă variabile de intrare (alfabetul
de intrare U). Variabilele y1, y2,...,yq reprezintă variabile de ieşire
(alfabetul de ieşire Y). Apar şi ieşirile secundare xi,t+1 care se
transmit cu întârzierile Di la intrările secundare xi,t.
Circuitele CLS se comportă ca nişte sisteme cu memorie, stările
indicând evoluţia sau istoria sistemului. Partea combinațională
realizează la un moment dat, pentru mărimile de intrare și
starea prezentă o procesare în vederea generării ieşirilor Y, dar
şi o procesare pentru generarea stării viitoare.
Funcţia de transfer
f: U x X Y
Funcţia de tranziţie a stărilor
g:UxX Y

35. CIRCUITE LOGICE SECVENȚIALE (CLS)

2.2. Automate finite asincrone
Dacă mărimile caracteristice ale CLS aparţin unor spaţii U, X, Y finite, circuitul logic
secvenţial se numeşte automat finit (FSM – Finite State Machine)
Automatele finite asincrone admit două tipuri de reprezentări Mealy şi Moore
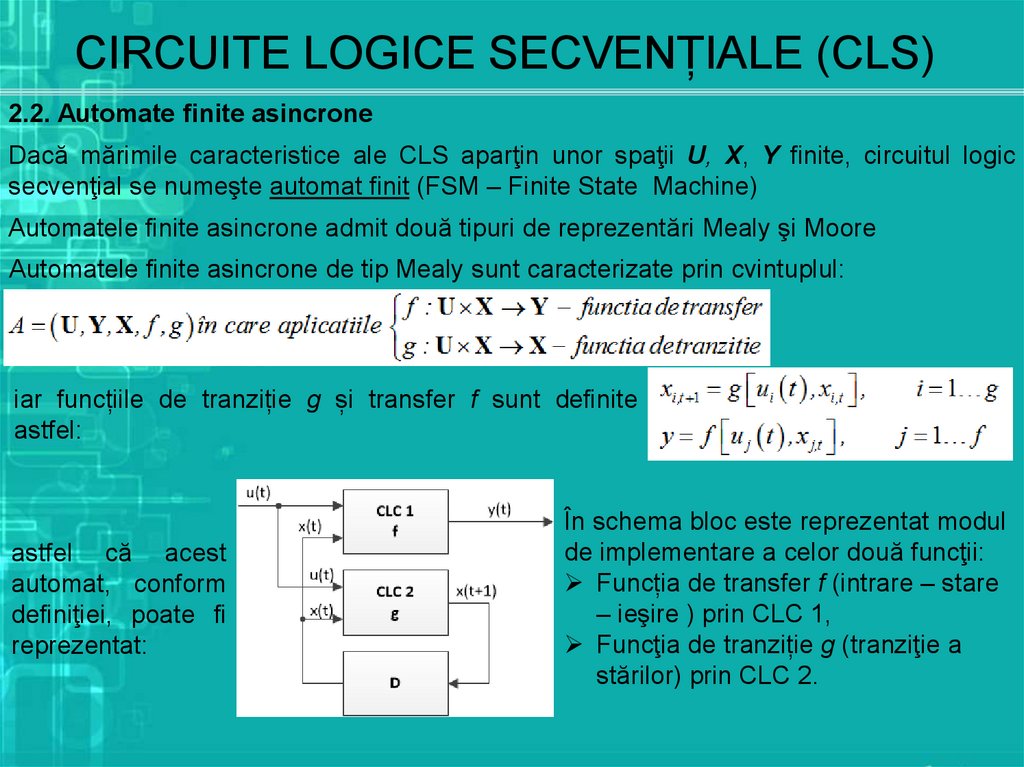
Automatele finite asincrone de tip Mealy sunt caracterizate prin cvintuplul:
iar funcțiile de tranziție g și transfer f sunt definite
astfel:
astfel că acest
automat, conform
definiţiei, poate fi
reprezentat:
În schema bloc este reprezentat modul
de implementare a celor două funcţii:
Funcția de transfer f (intrare – stare
– ieşire ) prin CLC 1,
Funcţia de tranziție g (tranziţie a
stărilor) prin CLC 2.

36. CIRCUITE LOGICE SECVENȚIALE (CLS)

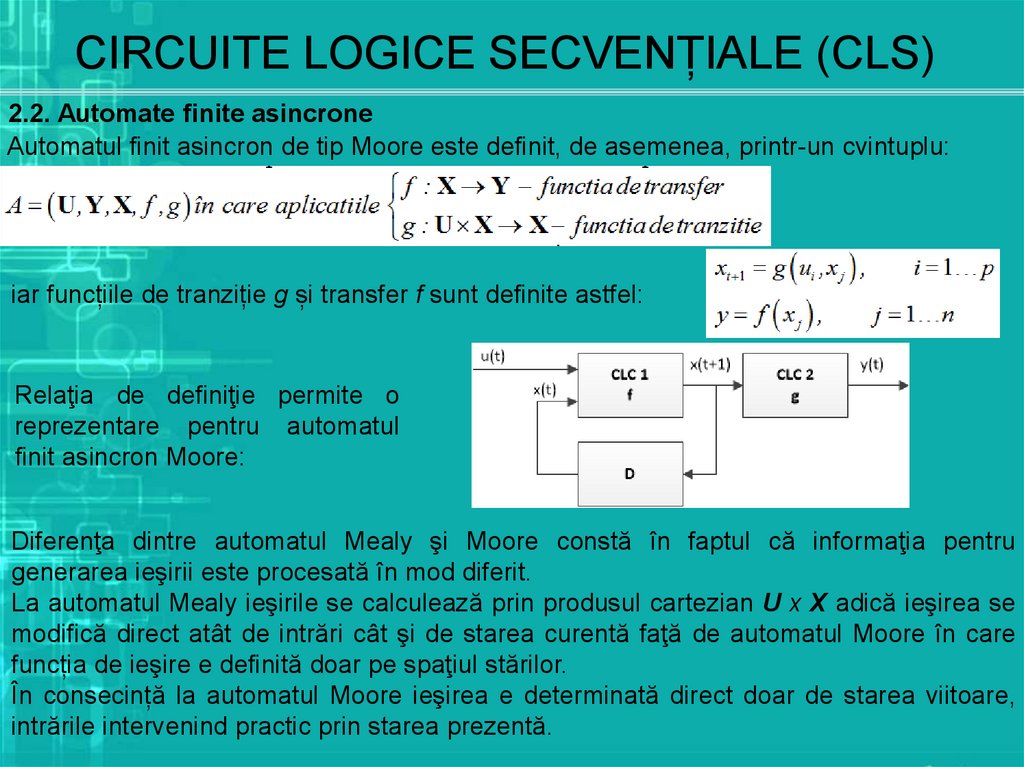
2.2. Automate finite asincrone
Automatul finit asincron de tip Moore este definit, de asemenea, printr-un cvintuplu:
iar funcțiile de tranziție g și transfer f sunt definite astfel:
Relaţia de definiţie permite o
reprezentare pentru automatul
finit asincron Moore:
Diferenţa dintre automatul Mealy şi Moore constă în faptul că informaţia pentru
generarea ieşirii este procesată în mod diferit.
La automatul Mealy ieşirile se calculează prin produsul cartezian U x X adică ieşirea se
modifică direct atât de intrări cât şi de starea curentă faţă de automatul Moore în care
funcția de ieşire e definită doar pe spaţiul stărilor.
În consecință la automatul Moore ieşirea e determinată direct doar de starea viitoare,
intrările intervenind practic prin starea prezentă.

37. CIRCUITE LOGICE SECVENȚIALE (CLS)

2.3. Automate finite sincrone
CLS sincrone au o structură similară celor asincrone cu deosebirea că elementele de
întârziere sunt substituite cu elemente de memorie sau regiştrii.
Şi în cazul automatelor sincrone apar cele două tipuri de automate: Mealy şi Moore.
Sub formă de schemă bloc acestea pot fi reprezentate similar prin înlocuirea elementului
de întârziere cu regiştrii (R) sau memorie (M). Înscrierea informaţiilor în registru sau
memorie se poate printr-un semnal periodic dreptunghiular de perioadă T, numit şi clock.
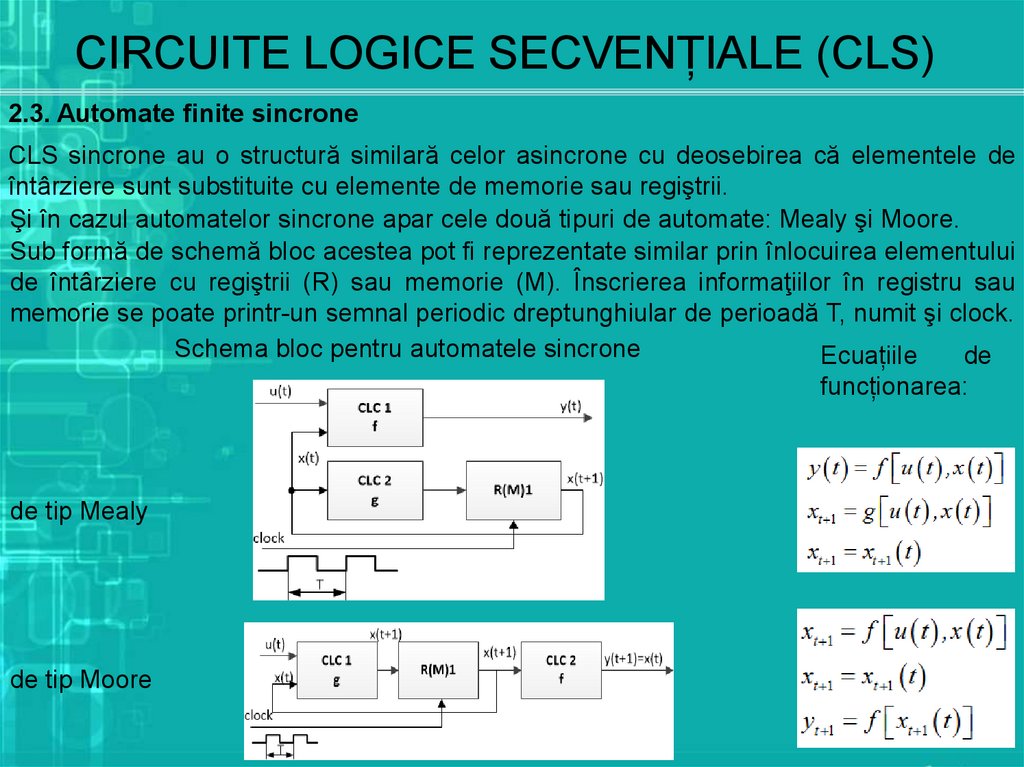
Schema bloc pentru automatele sincrone
Ecuațiile
de
funcționarea:
de tip Mealy
de tip Moore

38. CIRCUITE LOGICE SECVENȚIALE (CLS)

2.4. Reprezentarea CLS
În funcţie de modul de descriere, sunt utilizate 3 tipuri de reprezentări:
prin tabele de tranziţii,
grafuri de tranziţii
organigrame.
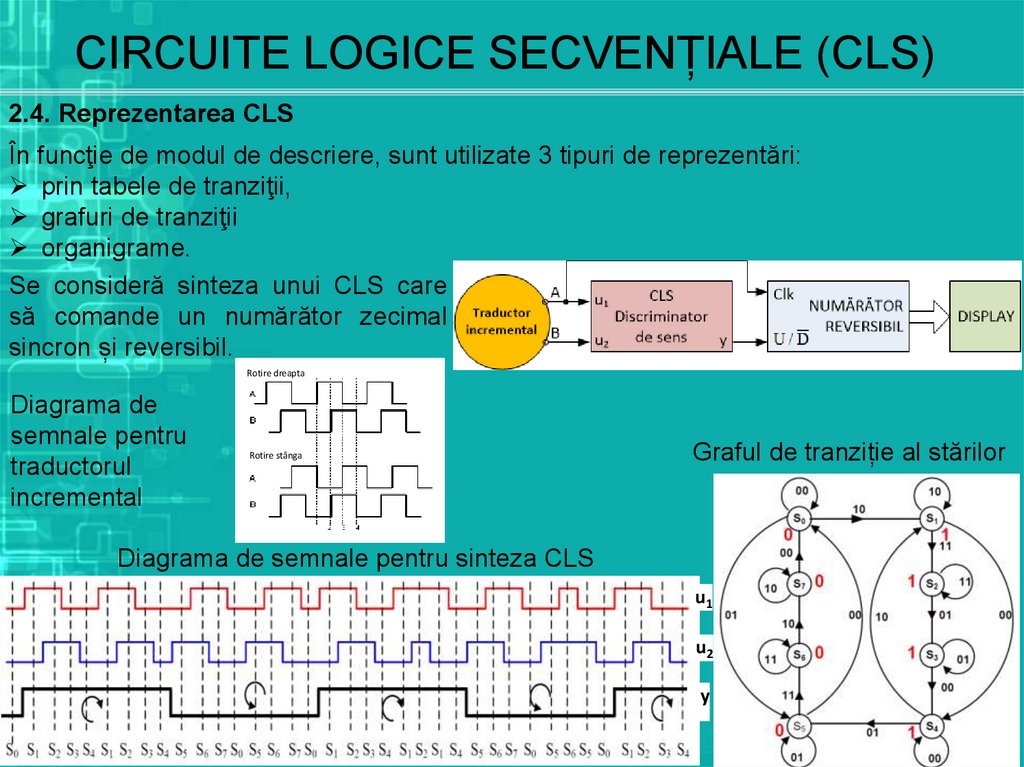
Se consideră sinteza unui CLS care
să comande un numărător zecimal
sincron și reversibil.
Rotire dreapta
Diagrama de
semnale pentru
traductorul
incremental
Rotire stânga
Graful de tranziție al stărilor
Diagrama de semnale pentru sinteza CLS
u1
u2
y

39. CIRCUITE LOGICE SECVENȚIALE (CLS)

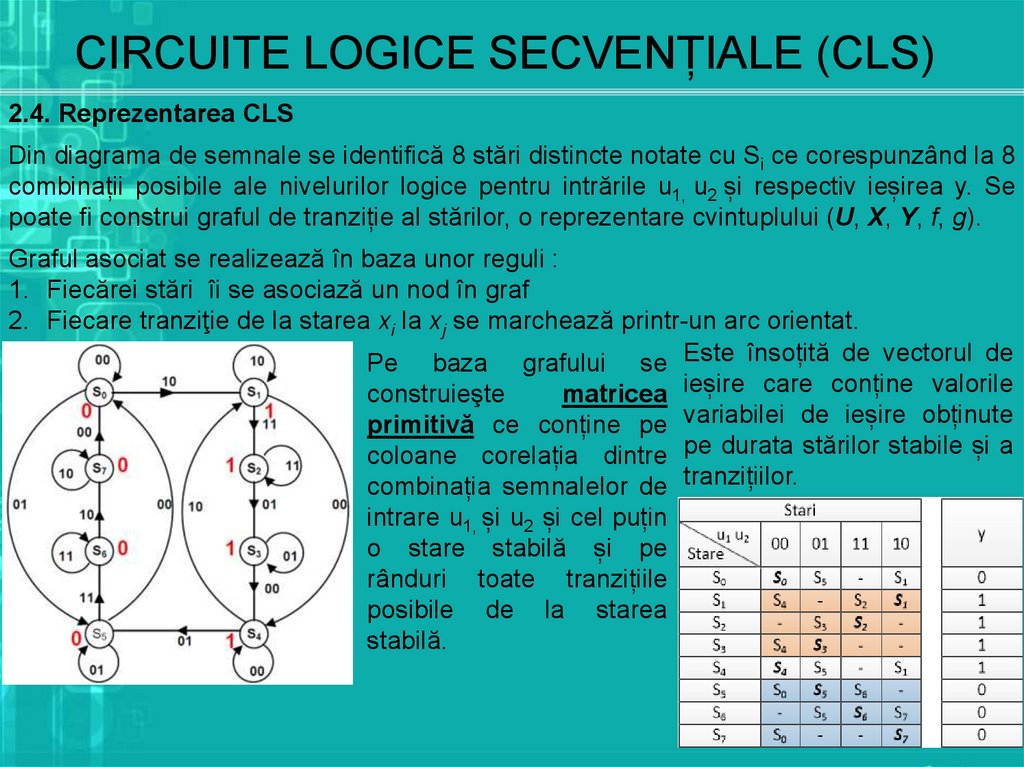
2.4. Reprezentarea CLS
Din diagrama de semnale se identifică 8 stări distincte notate cu Si ce corespunzând la 8
combinații posibile ale nivelurilor logice pentru intrările u1, u2 și respectiv ieșirea y. Se
poate fi construi graful de tranziție al stărilor, o reprezentare cvintuplului (U, X, Y, f, g).
Graful asociat se realizează în baza unor reguli :
1. Fiecărei stări îi se asociază un nod în graf
2. Fiecare tranziţie de la starea xi la xj se marchează printr-un arc orientat.
Pe baza grafului se Este însoțită de vectorul de
construieşte
matricea ieșire care conține valorile
primitivă ce conține pe variabilei de ieșire obținute
coloane corelația dintre pe durata stărilor stabile și a
combinația semnalelor de tranzițiilor.
intrare u1, și u2 și cel puțin
o stare stabilă și pe
rânduri toate tranzițiile
posibile de la starea
stabilă.

40. CIRCUITE LOGICE SECVENȚIALE (CLS)

2.4. Reprezentarea CLS
Pentru a identifica o configurație minimă a CLS este construită o matrice redusă de stări.
Reducerea de stărilor este realizată prin fuziune acelor linii, din matricea primitivă a
stărilor, între care nu există schimbări ale stărilor stabile. Se respectă următoarea reguli:
1. două linii ale matricei primitive a stărilor caracterizate de stările stabile i şi j se pot
alipi, dacă tranziţiile din aceste stări stabile conduc, prin alipirea aceloraşi valori ale
variabilelor de intrare, în starea stabilă viitoare unică k.
2. alipirea liniilor (stărilor) trebuie să ţină cont şi de concordanța ieşirilor.
Pentru a obține funcțiile de comutație variabilelor se
codifică stărilor matricei reduse. Se constată existența 4
stări reduse rezultă două variabile de stare necesare
pentru codificare și anume x1 și x2.

41. CIRCUITE LOGICE SECVENȚIALE (CLS)

2.4. Reprezentarea CLS
Pentru construirea funcţiilor de comutaţie ale stărilor x1 şi x2 este necesară construirea
matricelor tranziţiilor stărilor reduse în numărul egal cu numărul variabilelor de stare.
Conţinutul locaţiilor matricelor de tranziţie evidenţiază natura stării, astfel:
pentru o stare stabilă (la care x(t+Δt) = x(t)) conţinutul locaţiei este identic cu valoarea
variabilei de stare x cu care a fost codificată starea fuzionată din care face parte
respectiva stare stabilă;
pentru o stare instabilă conţinutul locaţiei este identic cu valoarea variabilei de stare
care a codificată starea stabilă corespunzătoare stării stabile considerate.
Aplicând metoda de sinteză a funcţiilor
logice bazată pe diagrame V-K se identifică
următoarele funcţii logice pentru variabilele
de excitaţie (stările) x1, x2 respectiv pentru
funcţia de ieşirea y, astfel:
Multisim

42.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
Din punct de vedere al structurii şi funcţionării CLS pot fi împărțite în trei categorii :
1. circuite basculante(circuite secvenţiale fundamentale);
2. numărătoare;
3. regiştri.
Circuitele basculante (CB) → definire → pot fi împărţite în trei categorii :
1. circuite basculante astabile, CBA;
2. circuite basculante monostabile, CBM
3. circuite basculante bistabile, CBB.
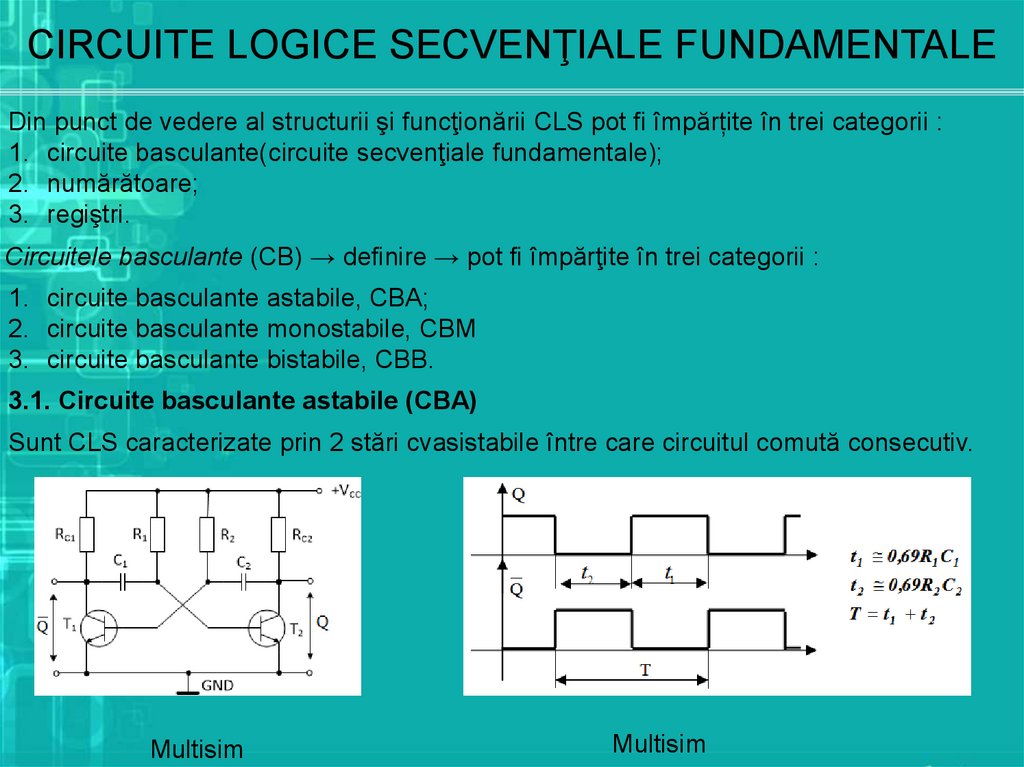
3.1. Circuite basculante astabile (CBA)
Sunt CLS caracterizate prin 2 stări cvasistabile între care circuitul comută consecutiv.
Multisim
Multisim

43.

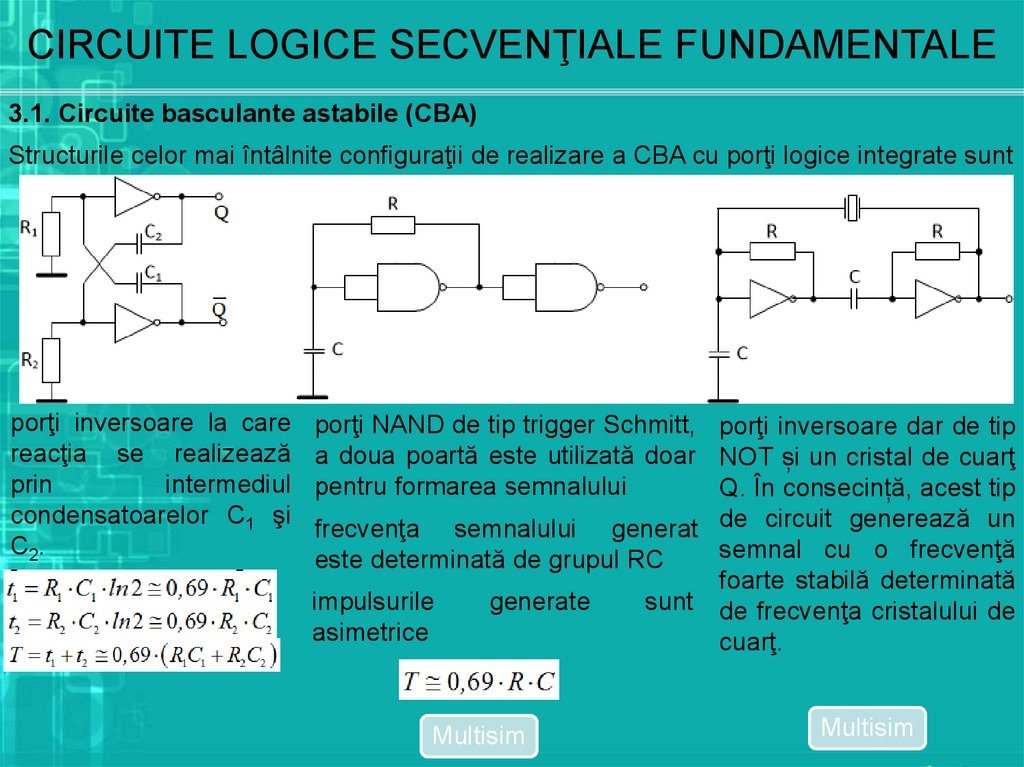
CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.1. Circuite basculante astabile (CBA)
Structurile celor mai întâlnite configuraţii de realizare a CBA cu porţi logice integrate sunt
porţi inversoare la care
reacţia se realizează
prin
intermediul
condensatoarelor C1 şi
C2.
porţi NAND de tip trigger Schmitt, porţi inversoare dar de tip
a doua poartă este utilizată doar NOT și un cristal de cuarţ
pentru formarea semnalului
Q. În consecință, acest tip
frecvenţa semnalului generat de circuit generează un
semnal cu o frecvenţă
este determinată de grupul RC
foarte stabilă determinată
impulsurile
generate
sunt de frecvenţa cristalului de
asimetrice
cuarţ.
Multisim
Multisim

44.

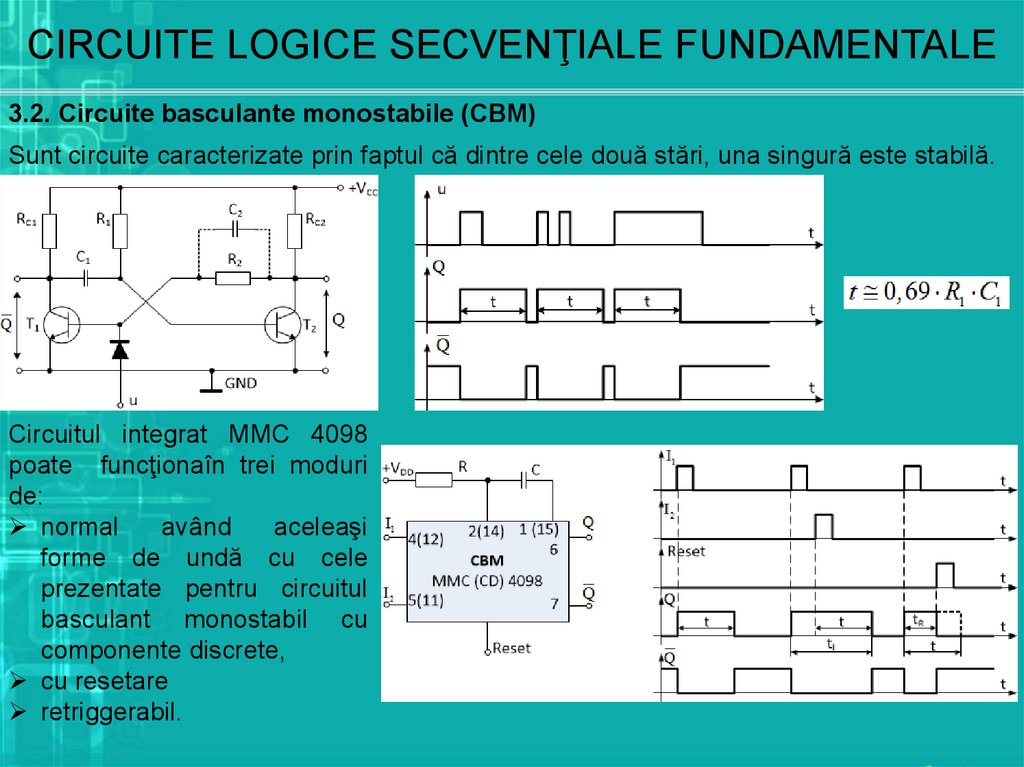
CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.2. Circuite basculante monostabile (CBM)
Sunt circuite caracterizate prin faptul că dintre cele două stări, una singură este stabilă.
Circuitul integrat MMC 4098
poate funcţionaîn trei moduri
de:
normal
având
aceleaşi
forme de undă cu cele
prezentate pentru circuitul
basculant monostabil cu
componente discrete,
cu resetare
retriggerabil.

45.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.3. Circuitul E555
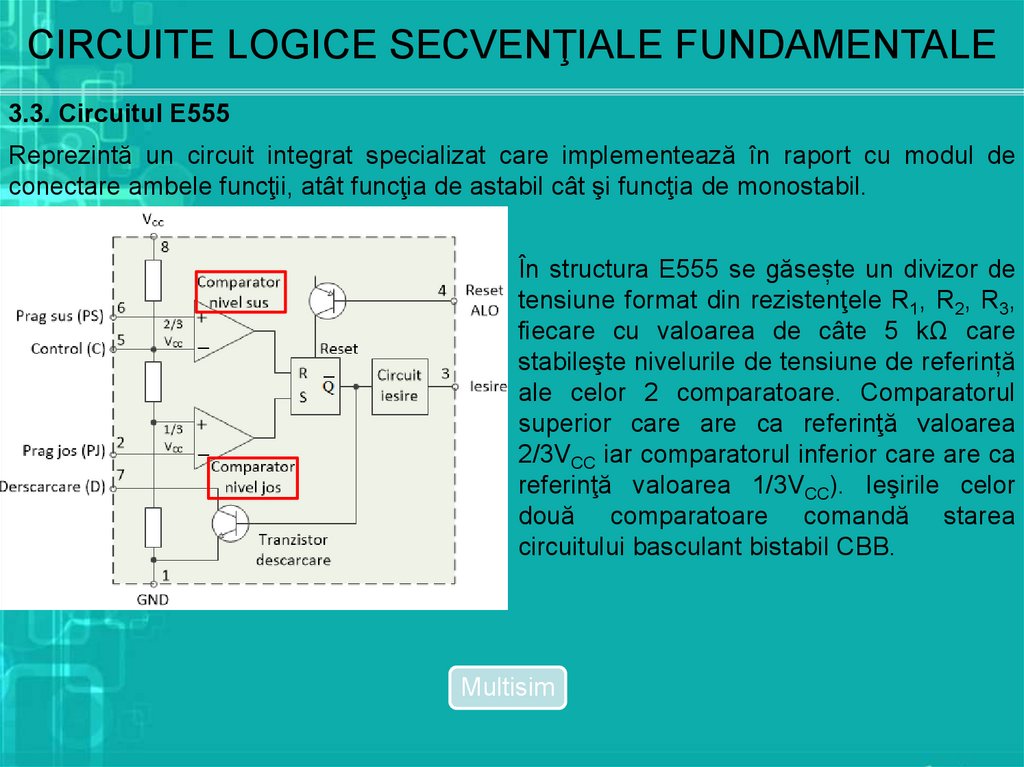
Reprezintă un circuit integrat specializat care implementează în raport cu modul de
conectare ambele funcţii, atât funcţia de astabil cât şi funcţia de monostabil.
În structura E555 se găsește un divizor de
tensiune format din rezistenţele R1, R2, R3,
fiecare cu valoarea de câte 5 kΩ care
stabileşte nivelurile de tensiune de referință
ale celor 2 comparatoare. Comparatorul
superior care are ca referinţă valoarea
2/3VCC iar comparatorul inferior care are ca
referinţă valoarea 1/3VCC). Ieşirile celor
două comparatoare comandă starea
circuitului basculant bistabil CBB.
Multisim

46.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.3. Circuitul E555
Funcţionarea circuitului în regim de astabil poate fi realizat în două moduri :
funcţionarea cu frecvenţă stabilită prin configuraţia circuitului;
funcţionarea controlată în tensiune.
Multisim

47.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.3. Circuitul E555
Funcţionarea ca monostabil a circuitului se obţine prin utilizarea unui buton conectat la
intrarea de control sau prin aplicarea unui semnalul de declanşare pe aceiaşi intrare.
Multisim

48.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.4. Circuite basculante de tip bistabil (CBB)
3.4.1. Definiţii. Structură. Clasificări.
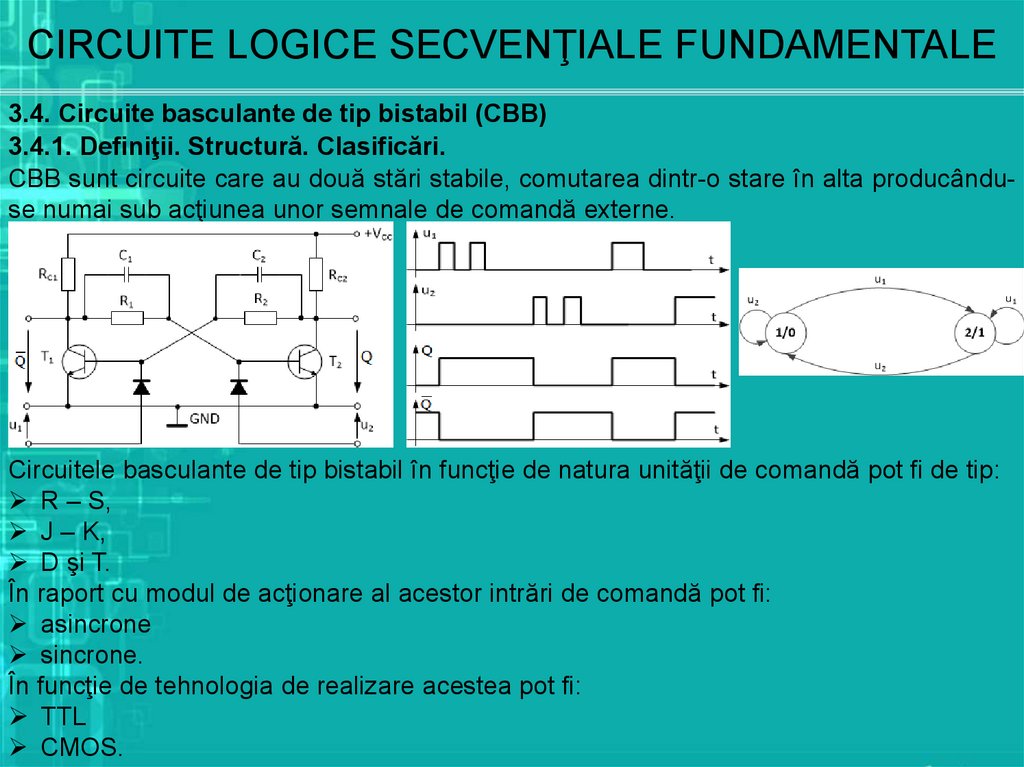
CBB sunt circuite care au două stări stabile, comutarea dintr-o stare în alta producânduse numai sub acţiunea unor semnale de comandă externe.
Circuitele basculante de tip bistabil în funcţie de natura unităţii de comandă pot fi de tip:
R – S,
J – K,
D şi T.
În raport cu modul de acţionare al acestor intrări de comandă pot fi:
asincrone
sincrone.
În funcţie de tehnologia de realizare acestea pot fi:
TTL
CMOS.

49.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.4.2. CBB de tip R-S
3.4.2.1. CBB de tip R-S asincrone
S – set (a pune, a înscrie) – este asociată cu stabilirea stării 1 şi respectiv a ieşirii Q = 1
R – reset (a şterge) – este asociată cu stabilirea stării 0 şi respectiv a ieşirii Q = 0
În vederea implementării cu porți logice a acestor bistabile se va realiza diagrama V-K,
pentru cele două ieșiri Qi 1 si Qi 1 considerând nivelele active pe 0 logic sau 1 logic.

50.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.4.2. CBB de tip R-S
3.4.2.1. CBB de tip R-S asincrone
Implementare NAND
Multisim
Implementare NOR
Multisim

51.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.4.2. CBB de tip R-S
3.4.2.2. CBB de tip R-S sincrone
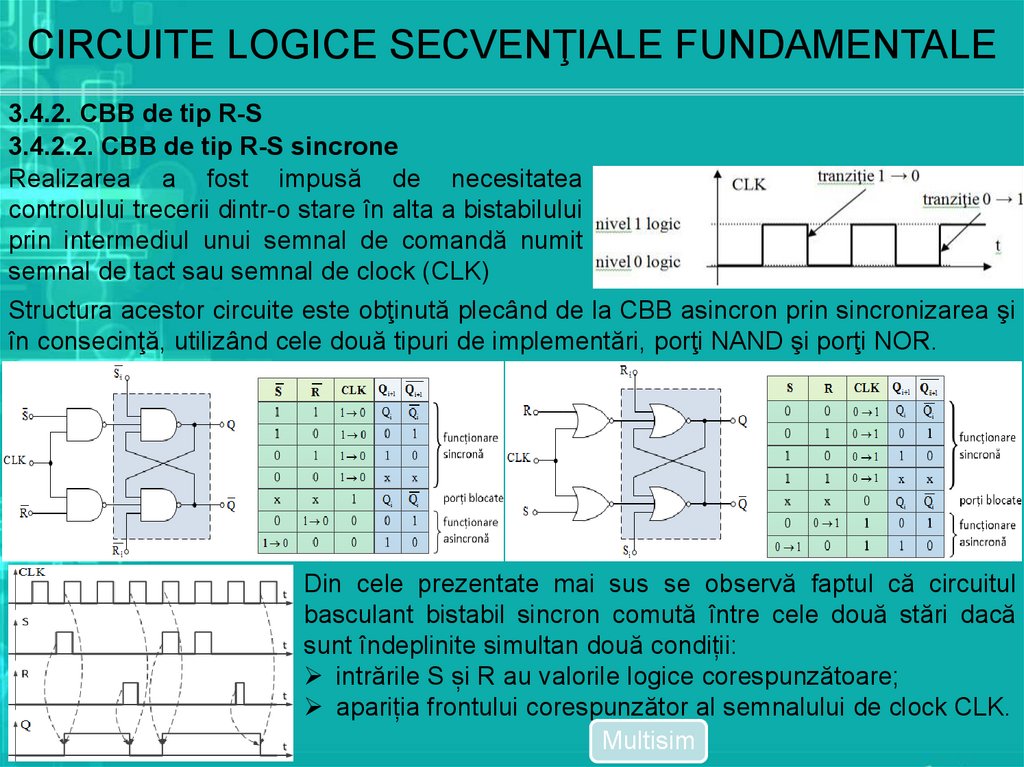
Realizarea a fost impusă de necesitatea
controlului trecerii dintr-o stare în alta a bistabilului
prin intermediul unui semnal de comandă numit
semnal de tact sau semnal de clock (CLK)
Structura acestor circuite este obţinută plecând de la CBB asincron prin sincronizarea şi
în consecinţă, utilizând cele două tipuri de implementări, porţi NAND şi porţi NOR.
Din cele prezentate mai sus se observă faptul că circuitul
basculant bistabil sincron comută între cele două stări dacă
sunt îndeplinite simultan două condiții:
intrările S și R au valorile logice corespunzătoare;
apariția frontului corespunzător al semnalului de clock CLK.
Multisim

52.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.4.2. CBB de tip R-S
3.4.2.3. CBB de tip R-S fără restricţii şi de tip Master – Slave
Există situații în funcționarea CBB de tip R-S în care restricțiile menționate nu pot fi
respectate și se impune utilizarea unor circuite CBB de tip R-S fără restricții. Acestea pot
fi obținute din cele cu restricții prin codificarea corespunzătoare a ieșirii nedefinite care
poate lua patru valori: 0, 1, Qi si Qi
După modul de codificare a stării nedefinite pot fi:
CBB R-S-Q – starea nedefinită se codifică prin Q
CBB R-S-S - starea nedefinită se codifică prin 1
CBB R-S-R - starea nedefinită se codifică prin 0
Pentru realizarea sintezei și obținerea modului de implementare se are în vedere faptul
că acești bistabili se obțin plecând de la bistabili cu restricții prin atașarea unor porți
auxiliare care să permită asigurarea codificării
Pentru sinteză se vor considera intrările active R și S ale bistabilului fără restricții care
trebui să comande intrările Ri și Si ale unui bistabil cu restricții cu nivelele active pe 0. Se
va considera că bistabilul trebuie să fie sincron astfel că la definirea funcțiilor logice se
va lua în calcul și semnalul de clock CLK.

53.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.4.2. CBB de tip R-S
3.4.2.3. CBB de tip R-S fără restricţii şi de tip Master – Slave
1. pentru bistabilul R-S-Q
Multisim
2. pentru bistabilul R-S-S
Multisim
pentru bistabilul R-S-R
Multisim

54.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.4.2. CBB de tip R-S
3.4.2.3. CBB de tip R-S fără restricţii şi de tip Master – Slave
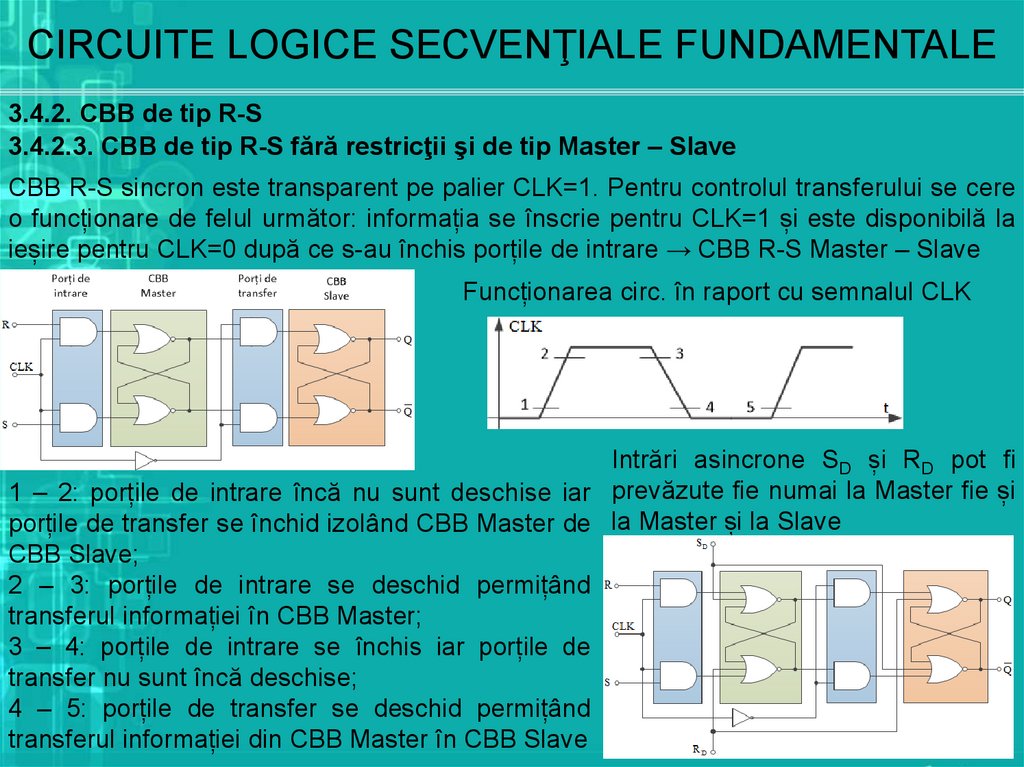
CBB R-S sincron este transparent pe palier CLK=1. Pentru controlul transferului se cere
o funcționare de felul următor: informația se înscrie pentru CLK=1 și este disponibilă la
ieșire pentru CLK=0 după ce s-au închis porțile de intrare → CBB R-S Master – Slave
Funcționarea circ. în raport cu semnalul CLK
Intrări asincrone SD și RD pot fi
1 – 2: porțile de intrare încă nu sunt deschise iar prevăzute fie numai la Master fie și
porțile de transfer se închid izolând CBB Master de la Master și la Slave
CBB Slave;
2 – 3: porțile de intrare se deschid permițând
transferul informației în CBB Master;
3 – 4: porțile de intrare se închis iar porțile de
transfer nu sunt încă deschise;
4 – 5: porțile de transfer se deschid permițând
transferul informației din CBB Master în CBB Slave

55.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.4.3. CBB de tip J-K
3.4.3.1. CBB de tip J-K asincron
Aceste CBB elimină nedeterminarea introdusă la CBB de tip R-S
Realizat dintrun CBB de tip
R-S la care se
atașează un
CLC
prin transformări
Qi 1 J Qi Qi K
pe baza algebrei logice
Qi 1 K Qi J Qi Qi
prin transformări
Qi 1 J Qi Qi K
pe baza algebrei logice
Qi 1 J Qi J Qi Qi
Schema CBB J-K

56.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.4.3. CBB de tip J-K
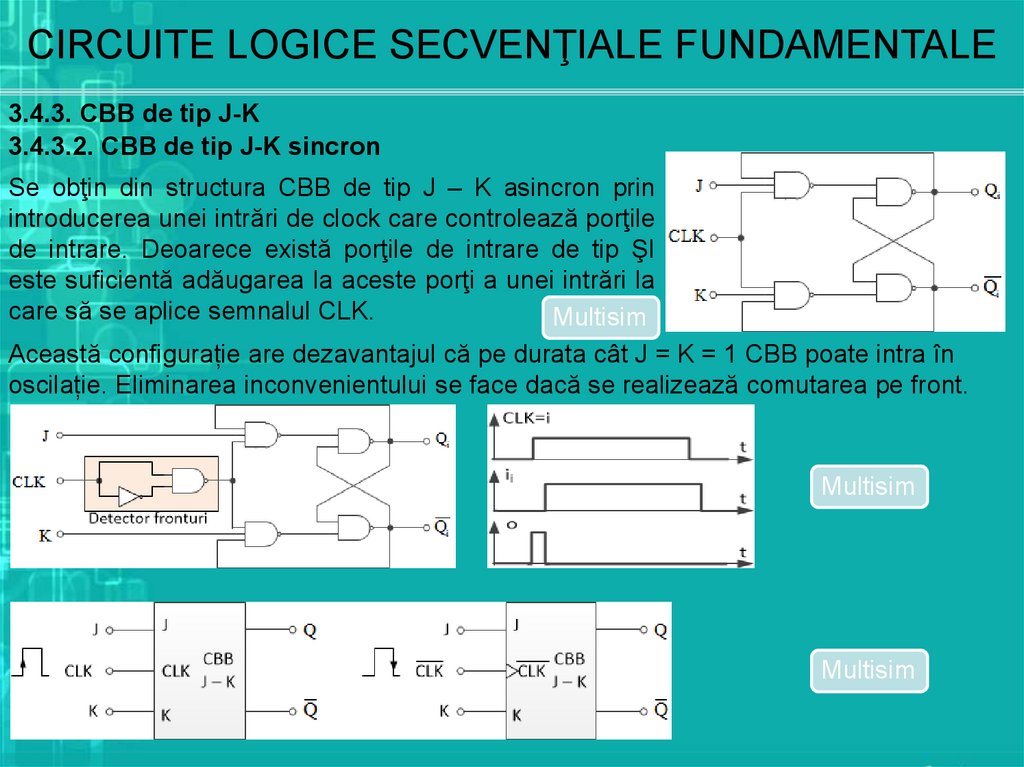
3.4.3.2. CBB de tip J-K sincron
Se obţin din structura CBB de tip J – K asincron prin
introducerea unei intrări de clock care controlează porţile
de intrare. Deoarece există porţile de intrare de tip ŞI
este suficientă adăugarea la aceste porţi a unei intrări la
care să se aplice semnalul CLK.
Multisim
Această configurație are dezavantajul că pe durata cât J = K = 1 CBB poate intra în
oscilație. Eliminarea inconvenientului se face dacă se realizează comutarea pe front.
Multisim
Multisim

57.

CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.4.3. CBB de tip J-K
3.4.3.2. CBB de tip J-K sincron
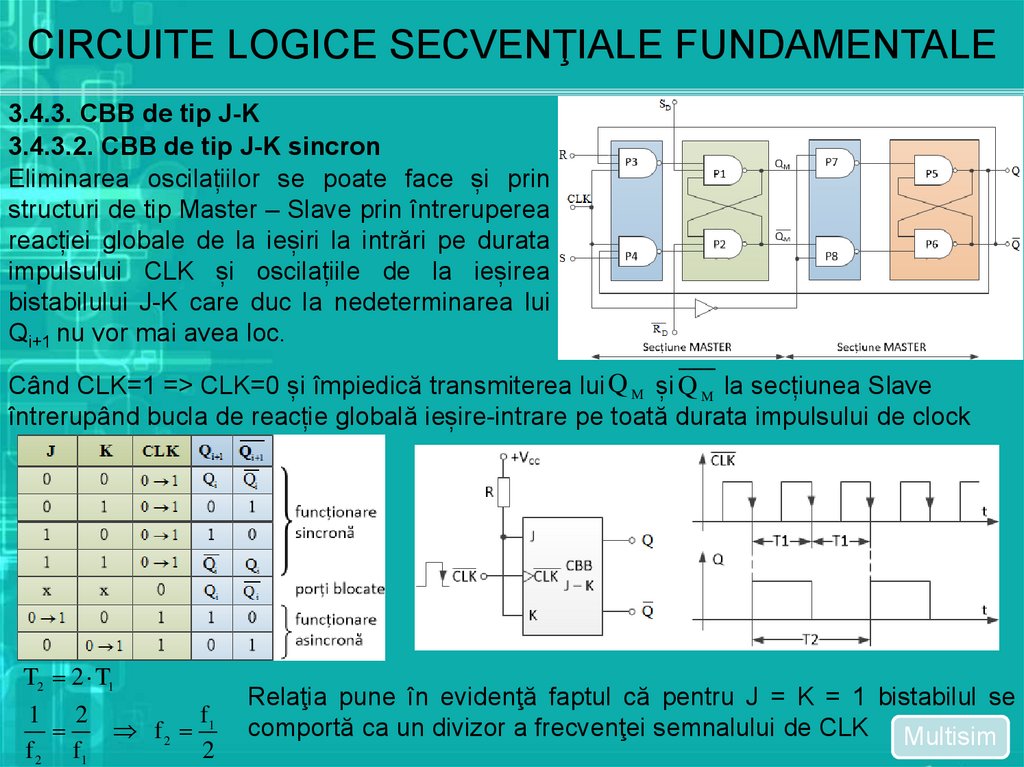
Eliminarea oscilațiilor se poate face și prin
structuri de tip Master – Slave prin întreruperea
reacției globale de la ieșiri la intrări pe durata
impulsului CLK și oscilațiile de la ieșirea
bistabilului J-K care duc la nedeterminarea lui
Qi+1 nu vor mai avea loc.
Când CLK=1 => CLK=0 și împiedică transmiterea lui Q M și Q M la secțiunea Slave
întrerupând bucla de reacție globală ieșire-intrare pe toată durata impulsului de clock
T2 2 T1
f
1 2
f2 1
f 2 f1
2
Relaţia pune în evidenţă faptul că pentru J = K = 1 bistabilul se
comportă ca un divizor a frecvenţei semnalului de CLK Multisim

58.

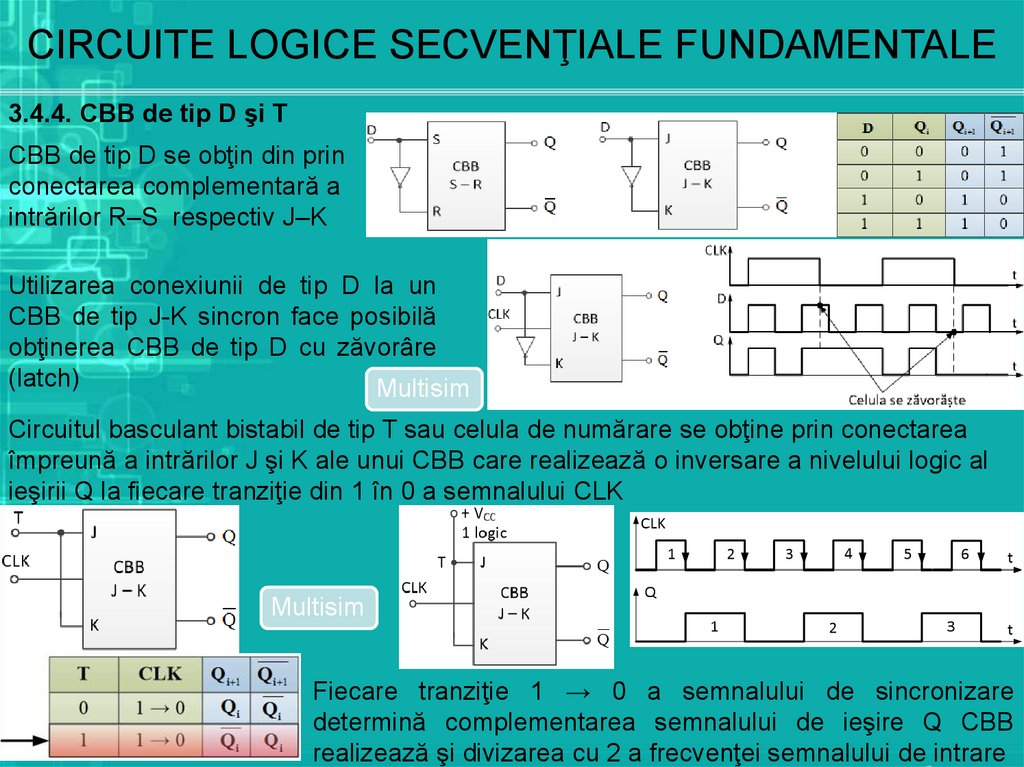
CIRCUITE LOGICE SECVENŢIALE FUNDAMENTALE
3.4.4. CBB de tip D şi T
CBB de tip D se obţin din prin
conectarea complementară a
intrărilor R–S respectiv J–K
Utilizarea conexiunii de tip D la un
CBB de tip J-K sincron face posibilă
obţinerea CBB de tip D cu zăvorâre
(latch)
Multisim
Circuitul basculant bistabil de tip T sau celula de numărare se obţine prin conectarea
împreună a intrărilor J şi K ale unui CBB care realizează o inversare a nivelului logic al
ieşirii Q la fiecare tranziţie din 1 în 0 a semnalului CLK
Multisim
Fiecare tranziţie 1 → 0 a semnalului de sincronizare
determină complementarea semnalului de ieşire Q CBB
realizează şi divizarea cu 2 a frecvenţei semnalului de intrare

59.

CIRCUITE DE NUMĂRARE
4.1.Definitii. Clasificări. Parametri.
Circuitele de numărare (numărătoarele) sunt CLC secvențiale ce numără (contorizează)
impulsurile aplicate la intrare şi sunt realizate prin interconectarea între ele a mai multor
celule elementare de numărare reprezentate de CBB tip T.
Numărătorul poate fi privit ca un circuit
secvențial cu un anumit număr de stări.
Numărul de stări posibile N ale unui
numărător format din n bistabili va fi N = 2n. În multe situații din cele 2n stări posibile se
elimină un anumit număr k stări si vor rămâne un număr p = 2n-k de stări.
1.
După modul de numărare:
directe;
inverse ;
reversibile.
3. După valoarea inițială :
neprogramabile;
programabile.
5. După numărul de stări:
Modulo 2n;
Modulo p.
2. După modul de funcționare:
asincrone –bistabilii comută succesiv;
sincrone – bistabilii comută simultan.
4.
După codul generat:
Binare;
BCD;
Decadice;
Alte coduri.
Principalii parametri ai
numărătorului sunt
capacitatea de numărare;
factorul de divizare;
timpul de propagare.

60.

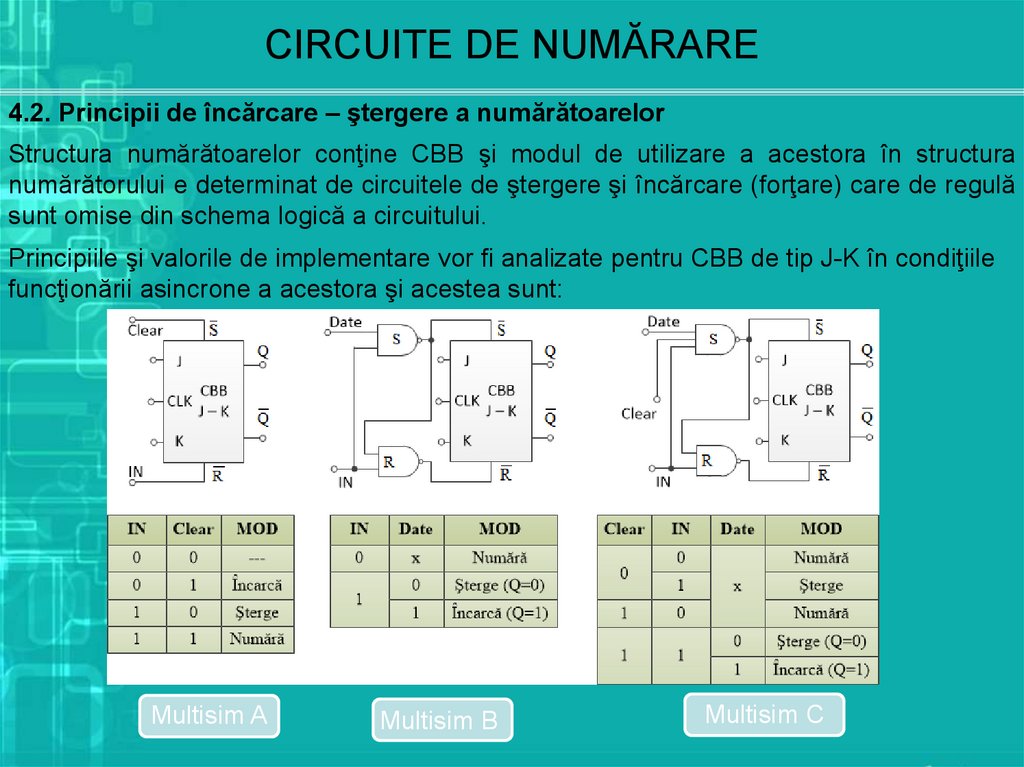
CIRCUITE DE NUMĂRARE
4.2. Principii de încărcare – ştergere a numărătoarelor
Structura numărătoarelor conţine CBB şi modul de utilizare a acestora în structura
numărătorului e determinat de circuitele de ştergere şi încărcare (forţare) care de regulă
sunt omise din schema logică a circuitului.
Principiile şi valorile de implementare vor fi analizate pentru CBB de tip J-K în condiţiile
funcţionării asincrone a acestora şi acestea sunt:
Multisim A
Multisim B
Multisim C

61.

CIRCUITE DE NUMĂRARE
4.2. Principii de încărcare – ştergere a numărătoarelor
Principiile şi valorile de implementare pentru CBB de tip J-K în condiţiile funcţionării
sincrone a acestora şi acestea sunt:
Multisim
Multisim
Multisim

62.

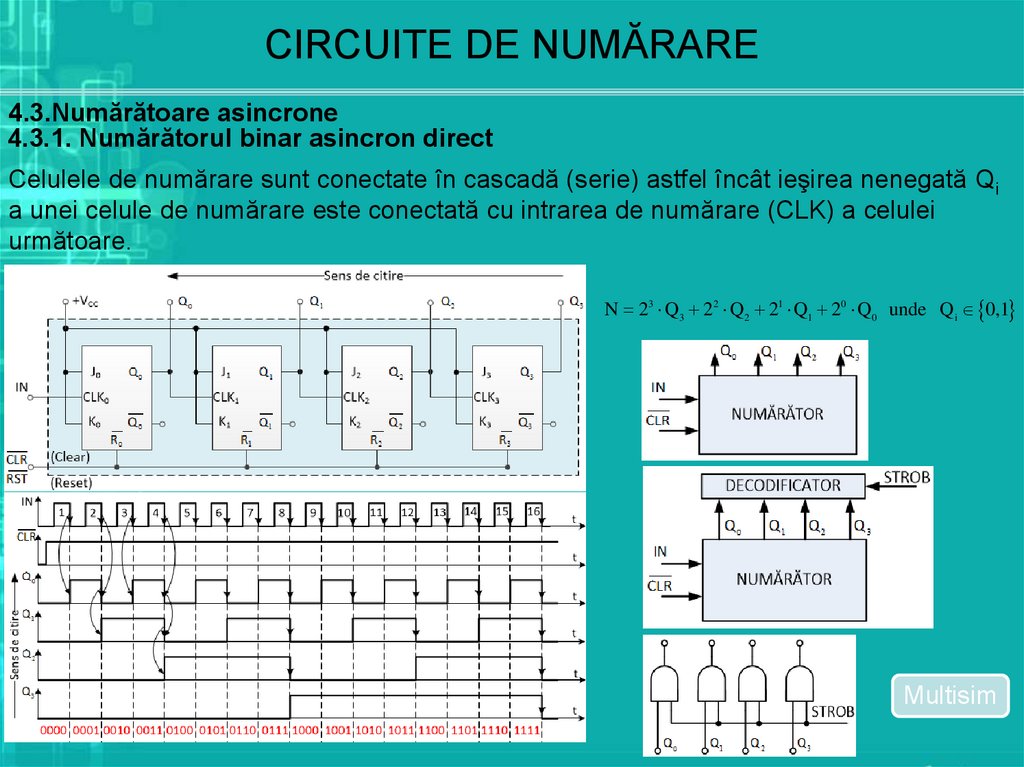
CIRCUITE DE NUMĂRARE
4.3.Numărătoare asincrone
4.3.1. Numărătorul binar asincron direct
Celulele de numărare sunt conectate în cascadă (serie) astfel încât ieşirea nenegată Qi
a unei celule de numărare este conectată cu intrarea de numărare (CLK) a celulei
următoare.
N 23 Q3 22 Q 2 21 Q1 20 Q 0 unde Q i 0,1
Multisim

63.

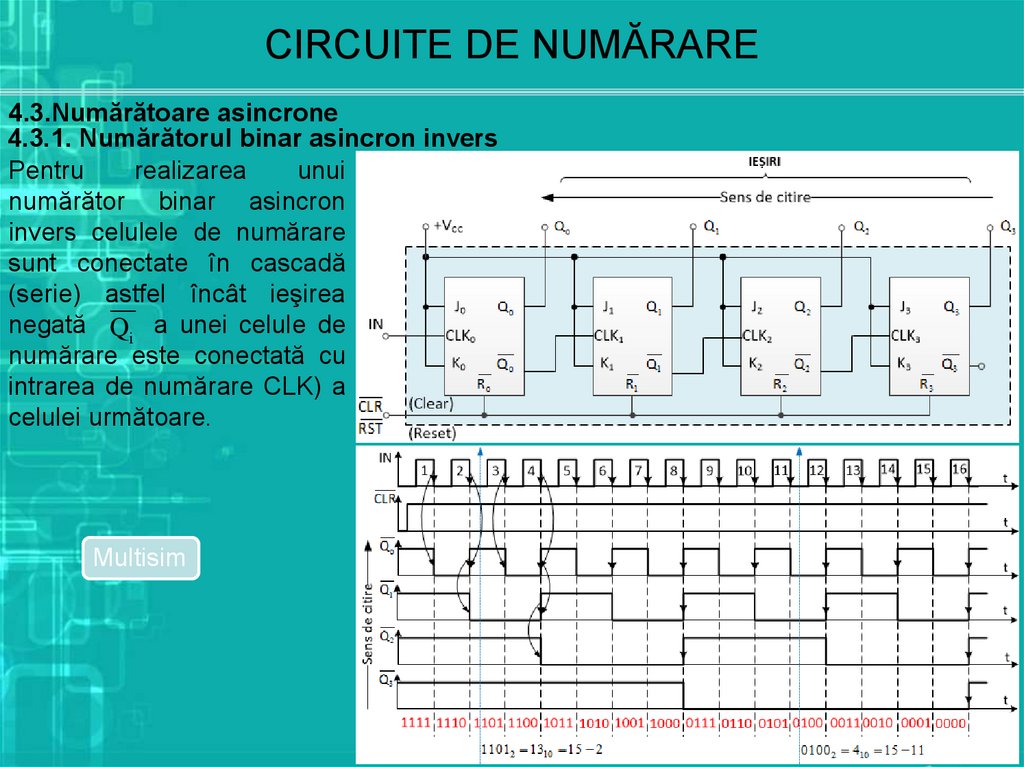
CIRCUITE DE NUMĂRARE
4.3.Numărătoare asincrone
4.3.1. Numărătorul binar asincron invers
Pentru
realizarea
unui
numărător binar asincron
invers celulele de numărare
sunt conectate în cascadă
(serie) astfel încât ieşirea
negată Qi a unei celule de
numărare este conectată cu
intrarea de numărare CLK) a
celulei următoare.
Multisim

64.

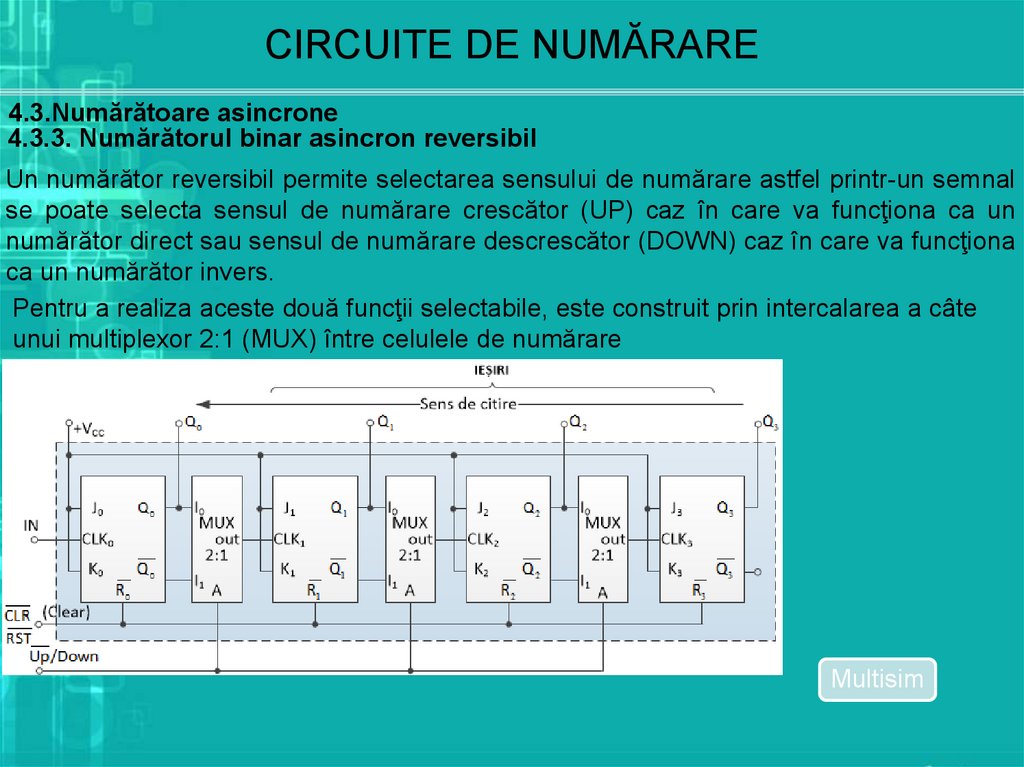
CIRCUITE DE NUMĂRARE
4.3.Numărătoare asincrone
4.3.3. Numărătorul binar asincron reversibil
Un numărător reversibil permite selectarea sensului de numărare astfel printr-un semnal
se poate selecta sensul de numărare crescător (UP) caz în care va funcţiona ca un
numărător direct sau sensul de numărare descrescător (DOWN) caz în care va funcţiona
ca un numărător invers.
Pentru a realiza aceste două funcţii selectabile, este construit prin intercalarea a câte
unui multiplexor 2:1 (MUX) între celulele de numărare
Multisim

65.

CIRCUITE DE NUMĂRARE
Tipuri de numărătoare binare asincrone
7493 sau variante
constructive (SN7493,
74LS93, 74S93)
4020 e un numărător
de 14 biţi
4060 este un numărător
cu oscilator de 14 biţi la
care sunt accesibile 11
ieşiri.

66.

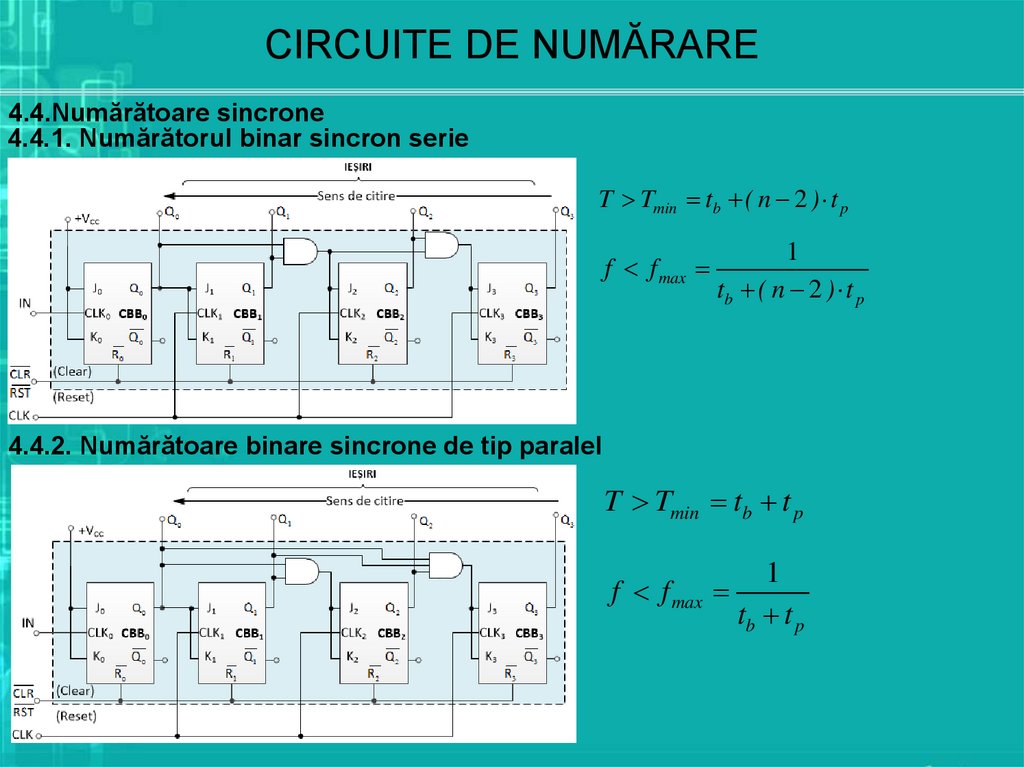
CIRCUITE DE NUMĂRARE
4.4.Numărătoare sincrone
4.4.1. Numărătorul binar sincron serie
Sunt realizate cu celule numărare comandate astfel încât acestea comută simultan sub
acţiunea unui impuls de clock comun. Numărătoarele sincrone pot fi: serie, paralel
CBB0 trebuie să comute la fiecare impuls aplicat la intrare,
deci trebuie să fie realizată configuraţia: J0 = K0 = 1
CBB1, trebuie să comute la fiecare două impulsuri aplicate la
intrare adică numai atunci când Q0 = 1, deci pentru acesta
trebuie să fie realizată configuraţia J1 = K1 = Q0
CBB2 trebuie să comute la fiecare pachet de 4 impulsuri la
intrare adică numai când şi Q1 şi Q0 sunt în 1 logic şi pentru
acesta trebuie să fie realizată configuraţia J2=K2= Q1 Q0
CBB3 trebuie să comute după fiecare pachet de 8 impulsuri
adică numai dacă şi Q2 şi Q1 şi Q0 sunt în 1 logic şi deci va
avea J3=K3= Q0 Q1 Q2 care poate fi scrisă J3=K3= Q0 Q1 Q2

67.

CIRCUITE DE NUMĂRARE
4.4.Numărătoare sincrone
4.4.1. Numărătorul binar sincron serie
T Tmin tb ( n 2 ) t p
f f max
1
tb ( n 2 ) t p
4.4.2. Numărătoare binare sincrone de tip paralel
T Tmin tb t p
f f max
1
tb t p

68.

CIRCUITE DE NUMĂRARE
4.4.Numărătoare sincrone
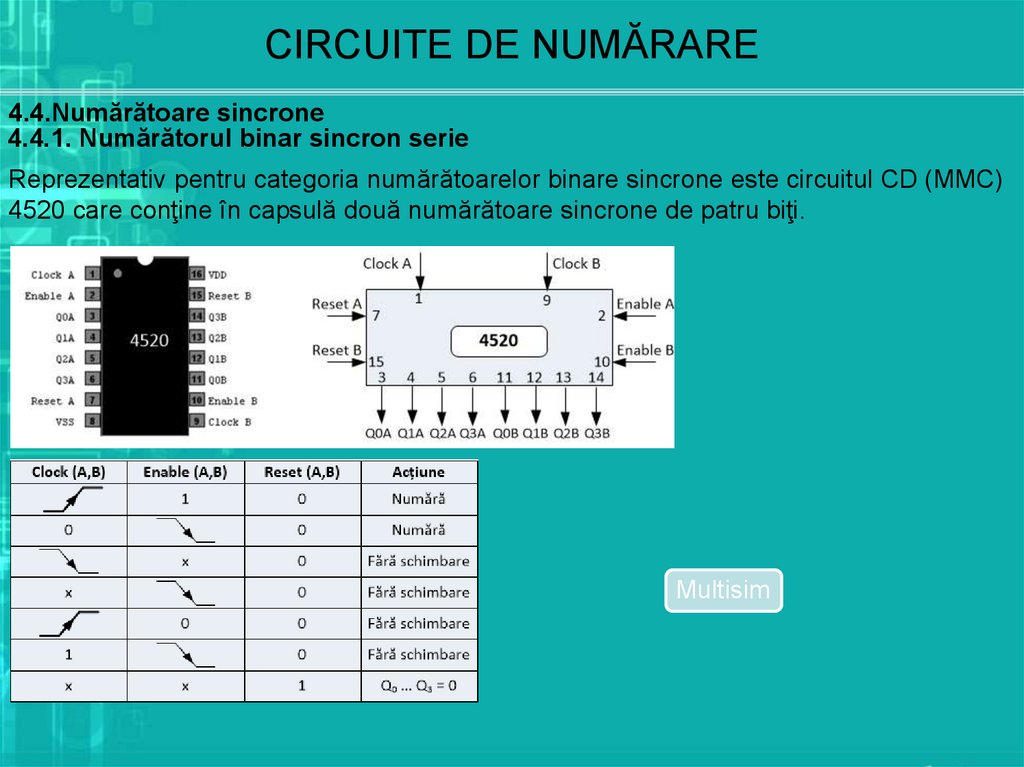
4.4.1. Numărătorul binar sincron serie
Reprezentativ pentru categoria numărătoarelor binare sincrone este circuitul CD (MMC)
4520 care conţine în capsulă două numărătoare sincrone de patru biţi.
Multisim

69.

CIRCUITE DE NUMĂRARE
4.4.Numărătoare sincrone
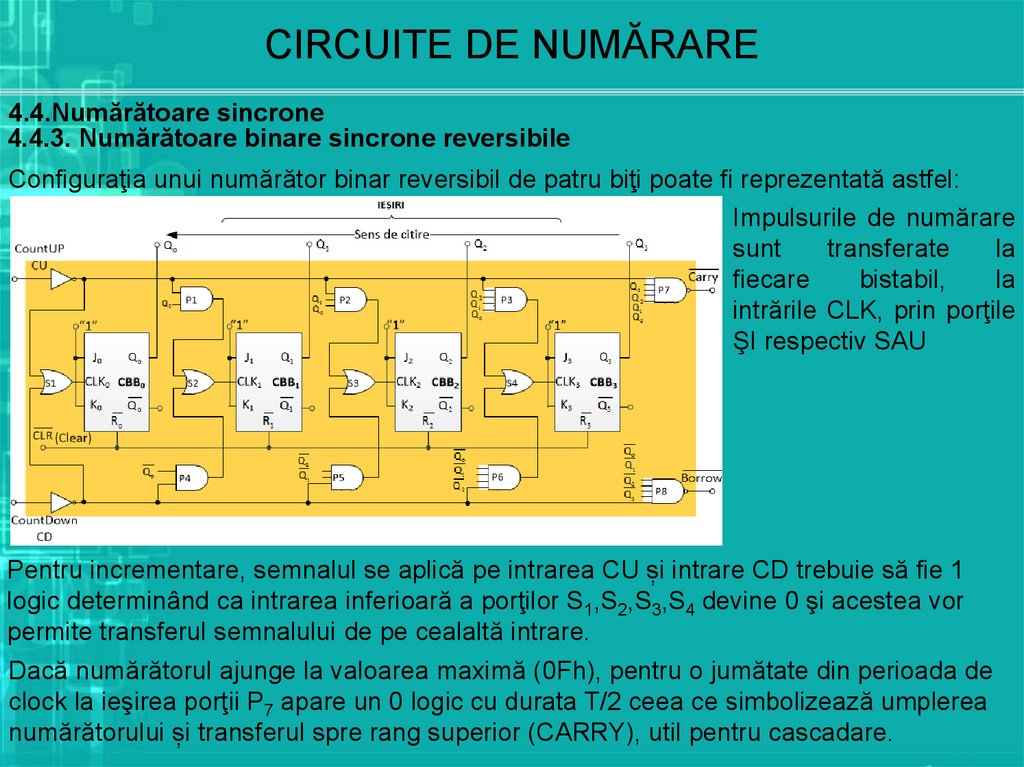
4.4.3. Numărătoare binare sincrone reversibile
Configuraţia unui numărător binar reversibil de patru biţi poate fi reprezentată astfel:
Impulsurile de numărare
sunt
transferate
la
fiecare
bistabil,
la
intrările CLK, prin porţile
ŞI respectiv SAU
Pentru incrementare, semnalul se aplică pe intrarea CU și intrare CD trebuie să fie 1
logic determinând ca intrarea inferioară a porţilor S1,S2,S3,S4 devine 0 şi acestea vor
permite transferul semnalului de pe cealaltă intrare.
Dacă numărătorul ajunge la valoarea maximă (0Fh), pentru o jumătate din perioada de
clock la ieşirea porţii P7 apare un 0 logic cu durata T/2 ceea ce simbolizează umplerea
numărătorului și transferul spre rang superior (CARRY), util pentru cascadare.

70.

CIRCUITE DE NUMĂRARE
4.4.Numărătoare sincrone
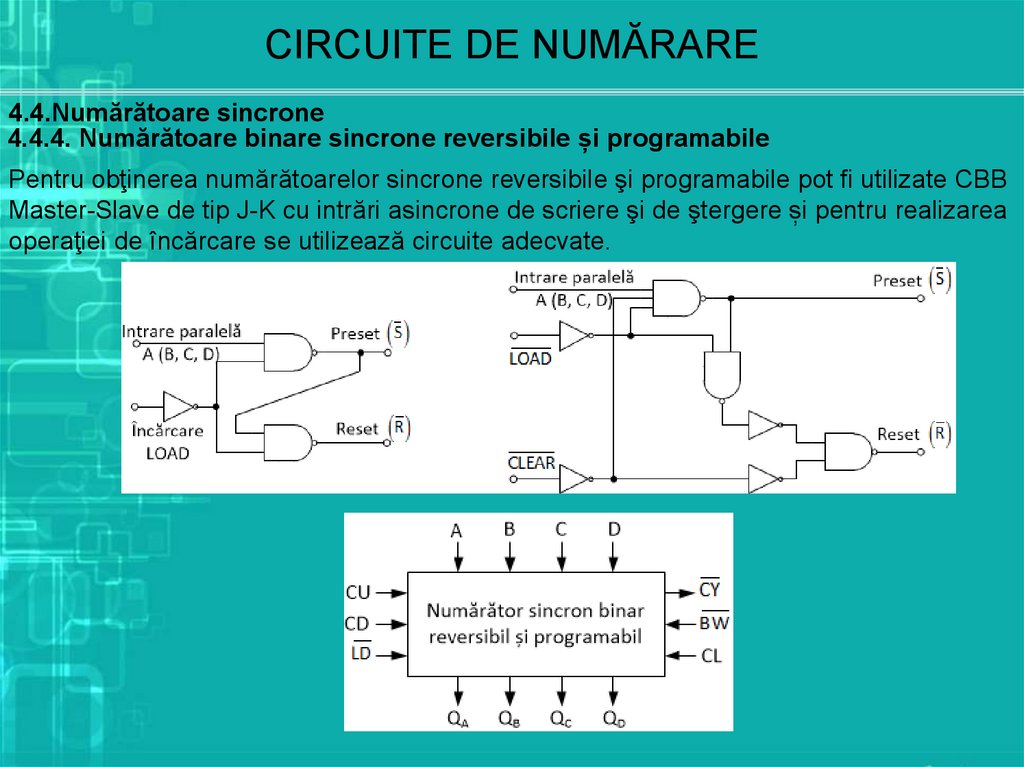
4.4.4. Numărătoare binare sincrone reversibile și programabile
Pentru obţinerea numărătoarelor sincrone reversibile şi programabile pot fi utilizate CBB
Master-Slave de tip J-K cu intrări asincrone de scriere şi de ştergere și pentru realizarea
operaţiei de încărcare se utilizează circuite adecvate.

71.

CIRCUITE DE NUMĂRARE
4.4.Numărătoare sincrone
4.4.4.1. Tipuri de numărătoare binare sincrone reversibile și programabile
Multisim
Multisim

72.

CIRCUITE DE NUMĂRARE
4.5.Numărătoare modulo p
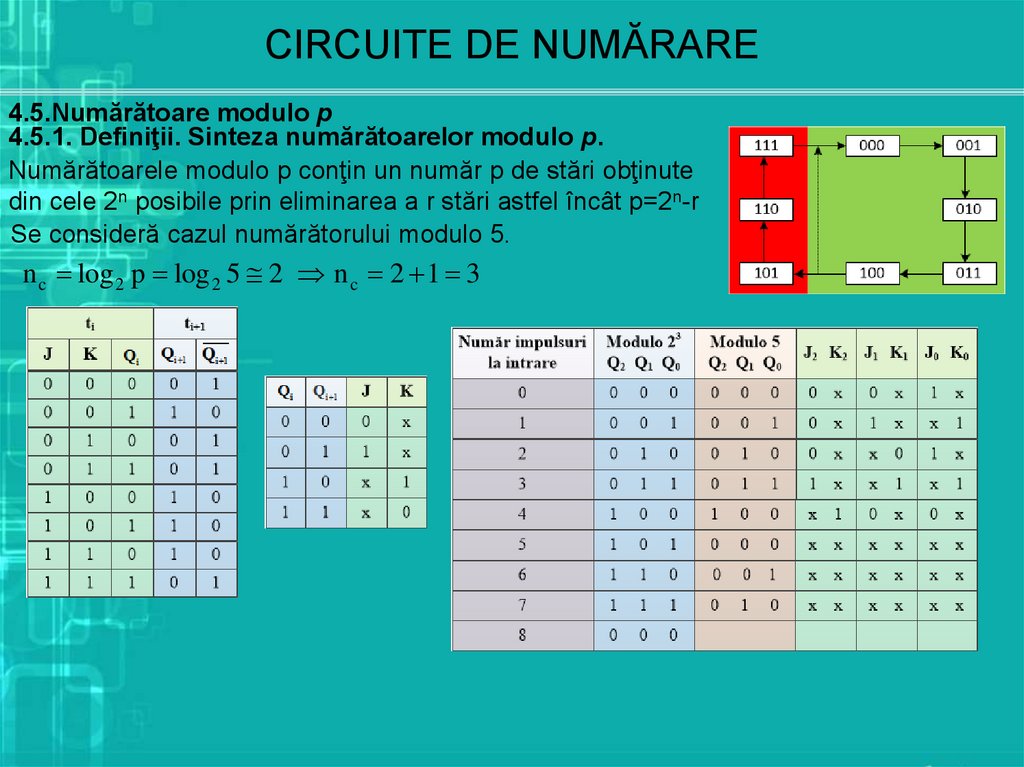
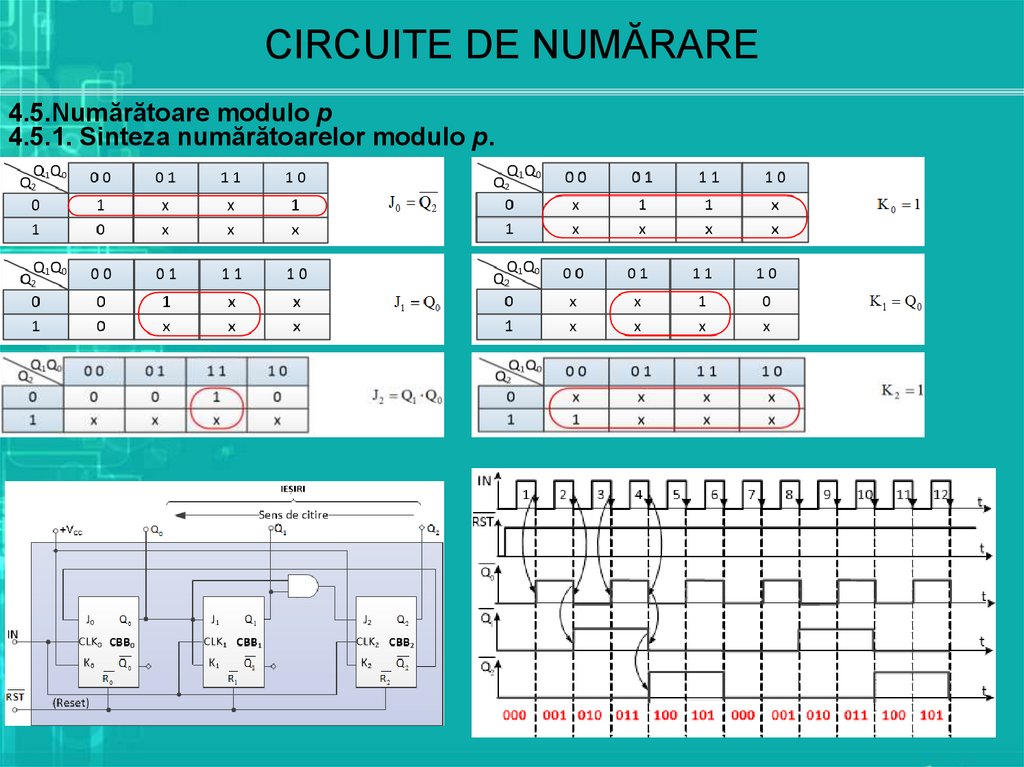
4.5.1. Definiţii. Sinteza numărătoarelor modulo p.
Numărătoarele modulo p conţin un număr p de stări obţinute
din cele 2n posibile prin eliminarea a r stări astfel încât p=2n-r
Se consideră cazul numărătorului modulo 5.
n c log 2 p log 2 5 2 n c 2 1 3

73.

CIRCUITE DE NUMĂRARE
4.5.Numărătoare modulo p
4.5.1. Sinteza numărătoarelor modulo p.

74.

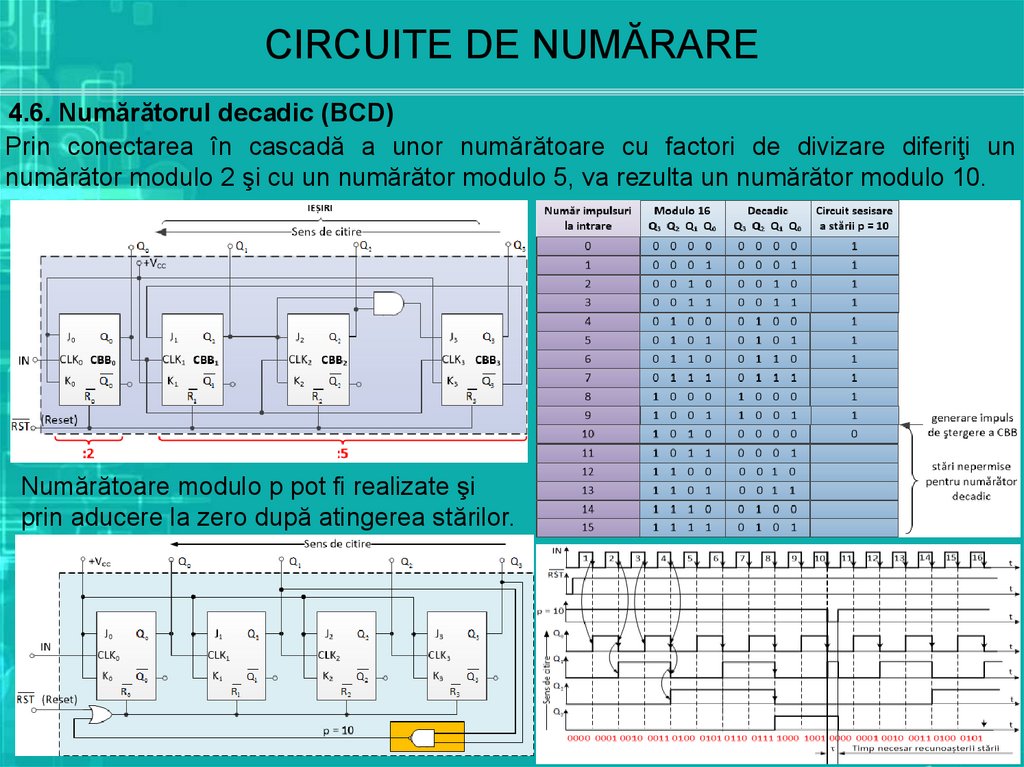
CIRCUITE DE NUMĂRARE
4.6. Numărătorul decadic (BCD)
Prin conectarea în cascadă a unor numărătoare cu factori de divizare diferiţi un
numărător modulo 2 şi cu un numărător modulo 5, va rezulta un numărător modulo 10.
Numărătoare modulo p pot fi realizate şi
prin aducere la zero după atingerea stărilor.

75.

CIRCUITE DE NUMĂRARE
4.6. Numărătorul decadic (BCD)
4.6.1. Tipuri de numărătoare decadice.
Multisim

76.

REGISTRE
5.1. Definiţii. Clasificări.
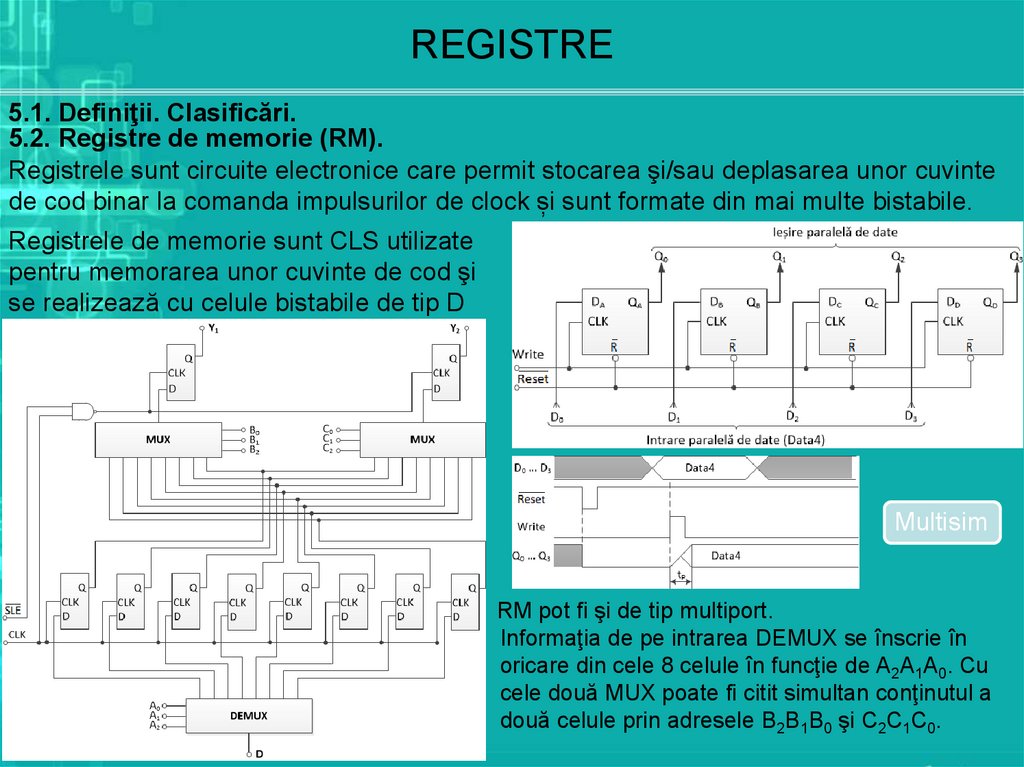
5.2. Registre de memorie (RM).
Registrele sunt circuite electronice care permit stocarea şi/sau deplasarea unor cuvinte
de cod binar la comanda impulsurilor de clock și sunt formate din mai multe bistabile.
Registrele de memorie sunt CLS utilizate
pentru memorarea unor cuvinte de cod şi
se realizează cu celule bistabile de tip D
Multisim
RM pot fi şi de tip multiport.
Informaţia de pe intrarea DEMUX se înscrie în
oricare din cele 8 celule în funcţie de A2A1A0. Cu
cele două MUX poate fi citit simultan conţinutul a
două celule prin adresele B2B1B0 şi C2C1C0.

77.

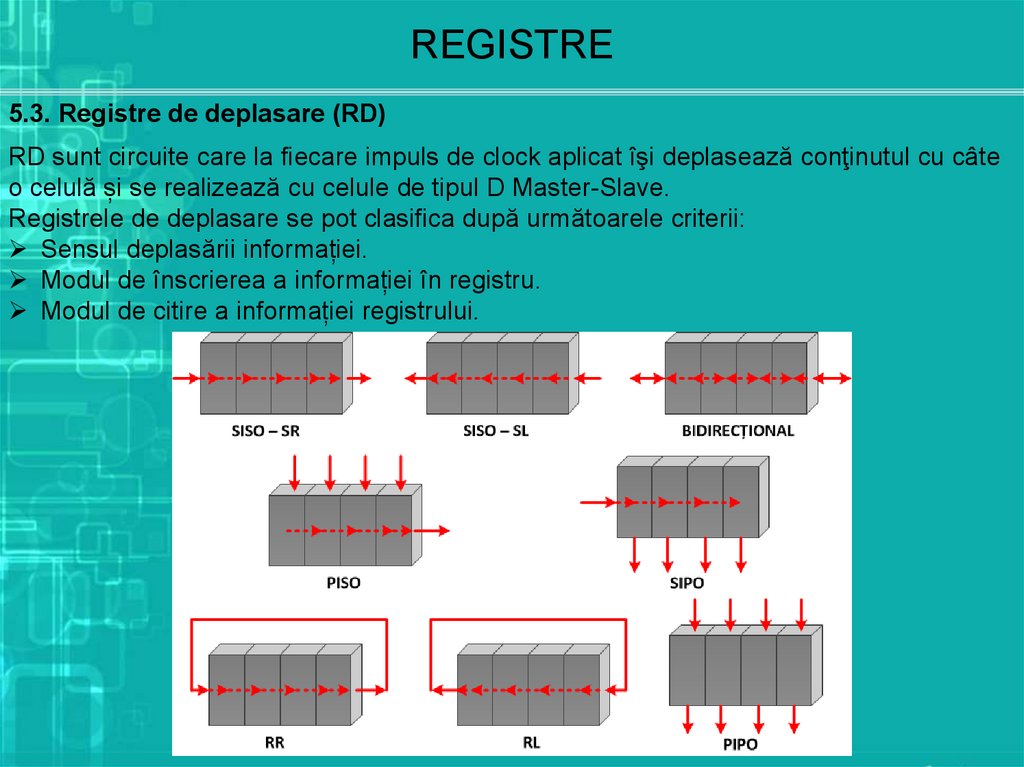
REGISTRE
5.3. Registre de deplasare (RD)
RD sunt circuite care la fiecare impuls de clock aplicat îşi deplasează conţinutul cu câte
o celulă și se realizează cu celule de tipul D Master-Slave.
Registrele de deplasare se pot clasifica după următoarele criterii:
Sensul deplasării informației.
Modul de înscrierea a informației în registru.
Modul de citire a informației registrului.

78.

REGISTRE
5.3. Registre de deplasare (RD)
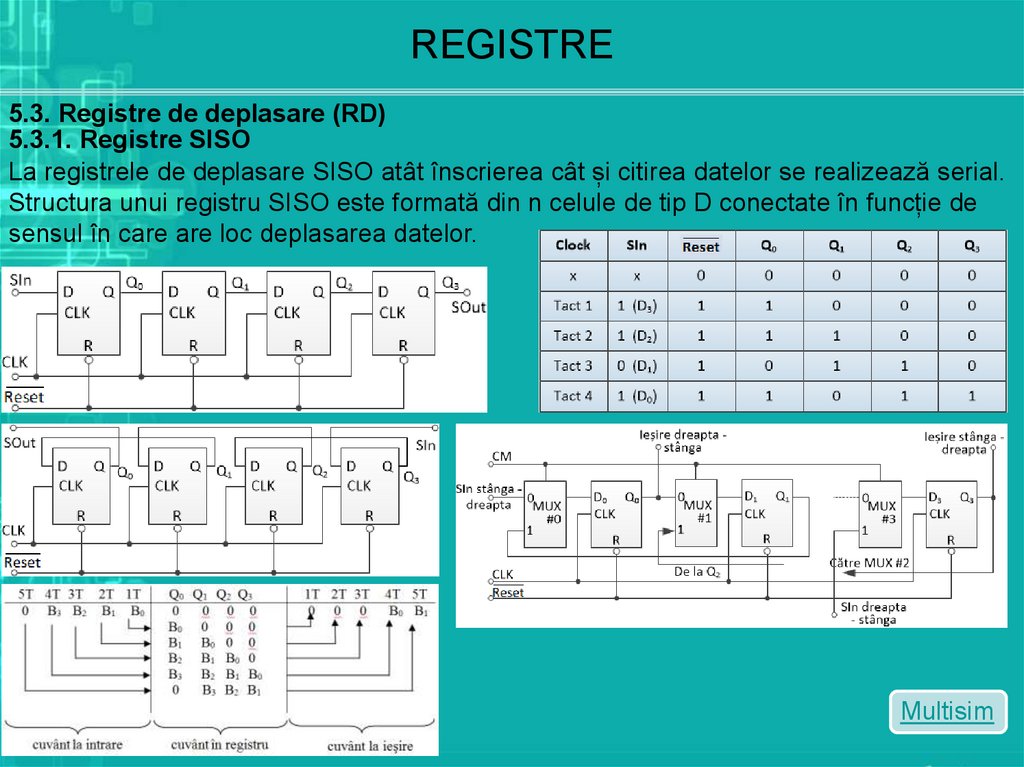
5.3.1. Registre SISO
La registrele de deplasare SISO atât înscrierea cât și citirea datelor se realizează serial.
Structura unui registru SISO este formată din n celule de tip D conectate în funcție de
sensul în care are loc deplasarea datelor.
Multisim

79.

REGISTRE
5.3. Registre de deplasare (RD)
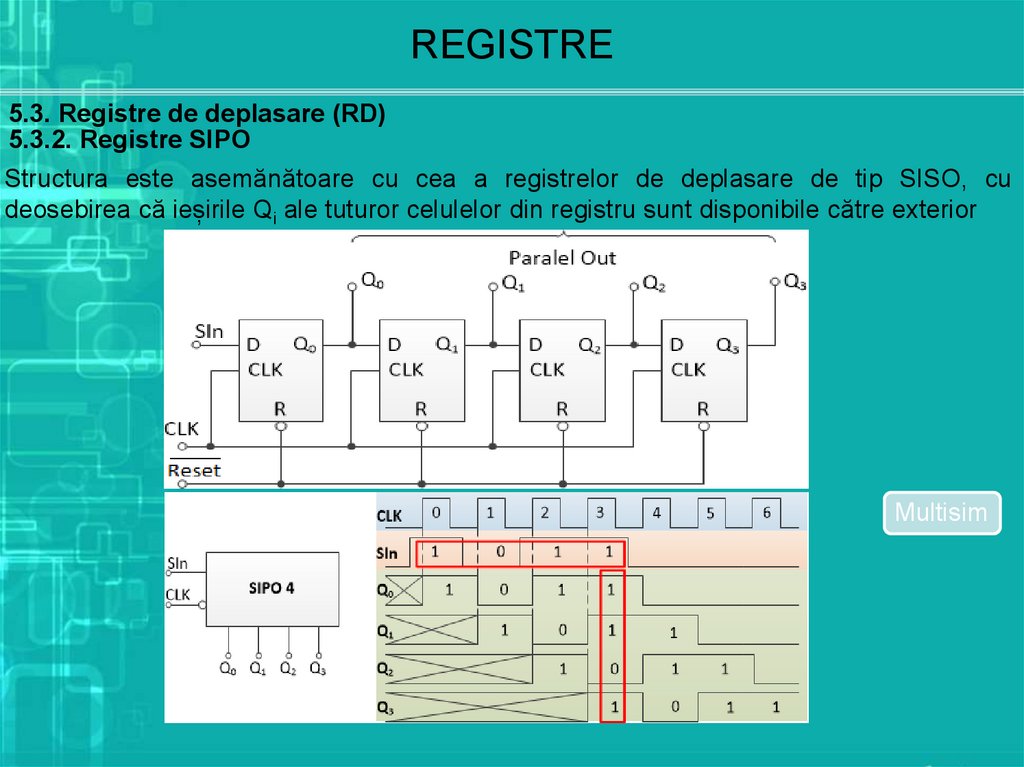
5.3.2. Registre SIPO
Structura este asemănătoare cu cea a registrelor de deplasare de tip SISO, cu
deosebirea că ieșirile Qi ale tuturor celulelor din registru sunt disponibile către exterior
Multisim

80.

REGISTRE
5.3. Registre de deplasare (RD)
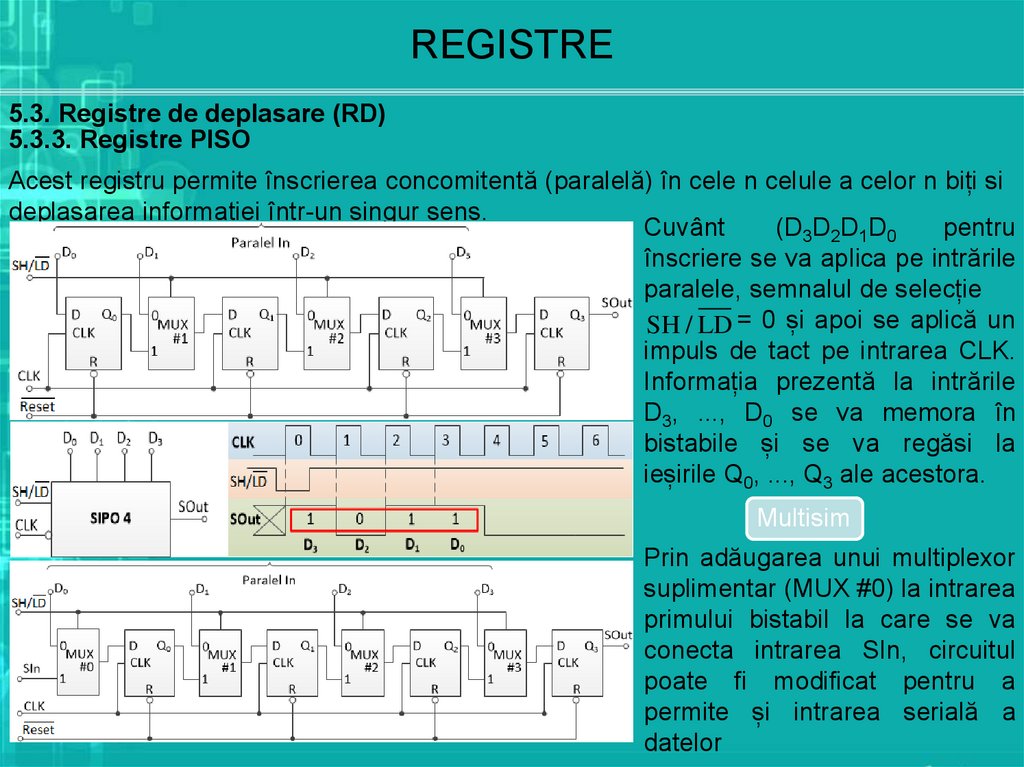
5.3.3. Registre PISO
Acest registru permite înscrierea concomitentă (paralelă) în cele n celule a celor n biți si
deplasarea informației într-un singur sens.
Cuvânt
(D3D2D1D0
pentru
înscriere se va aplica pe intrările
paralele, semnalul de selecție
SH / LD = 0 și apoi se aplică un
impuls de tact pe intrarea CLK.
Informația prezentă la intrările
D3, ..., D0 se va memora în
bistabile și se va regăsi la
ieșirile Q0, ..., Q3 ale acestora.
Multisim
Prin adăugarea unui multiplexor
suplimentar (MUX #0) la intrarea
primului bistabil la care se va
conecta intrarea SIn, circuitul
poate fi modificat pentru a
permite și intrarea serială a
datelor

81.

REGISTRE
5.3. Registre de deplasare (RD)
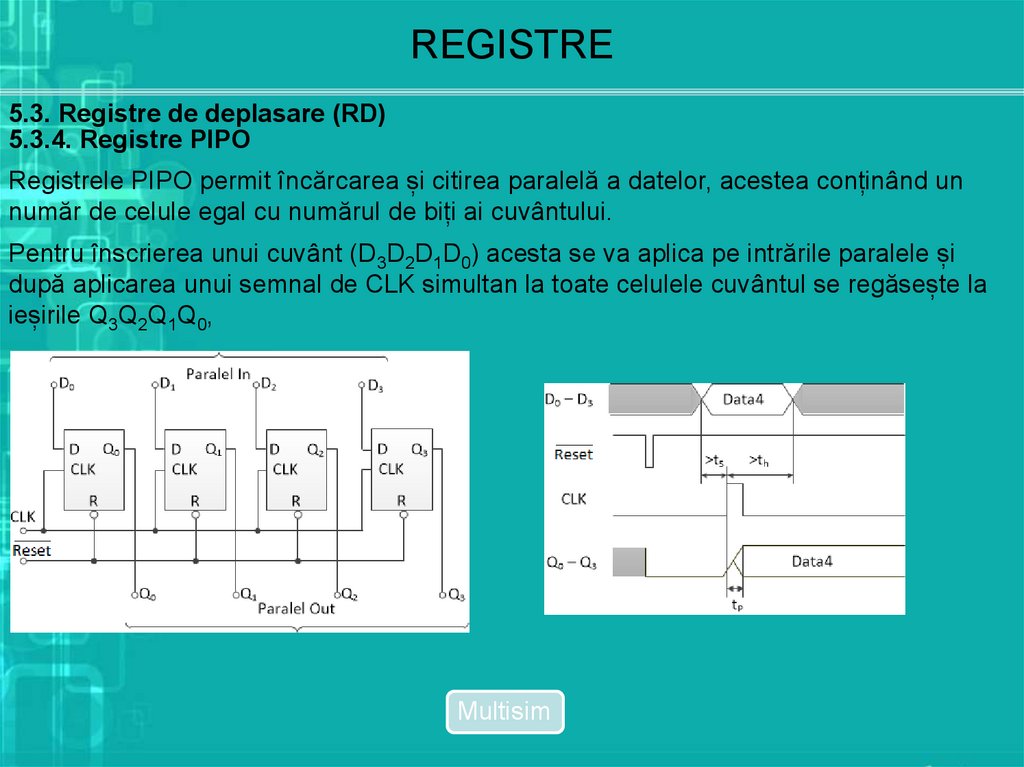
5.3.4. Registre PIPO
Registrele PIPO permit încărcarea și citirea paralelă a datelor, acestea conținând un
număr de celule egal cu numărul de biți ai cuvântului.
Pentru înscrierea unui cuvânt (D3D2D1D0) acesta se va aplica pe intrările paralele și
după aplicarea unui semnal de CLK simultan la toate celulele cuvântul se regăsește la
ieșirile Q3Q2Q1Q0,
Multisim

82.

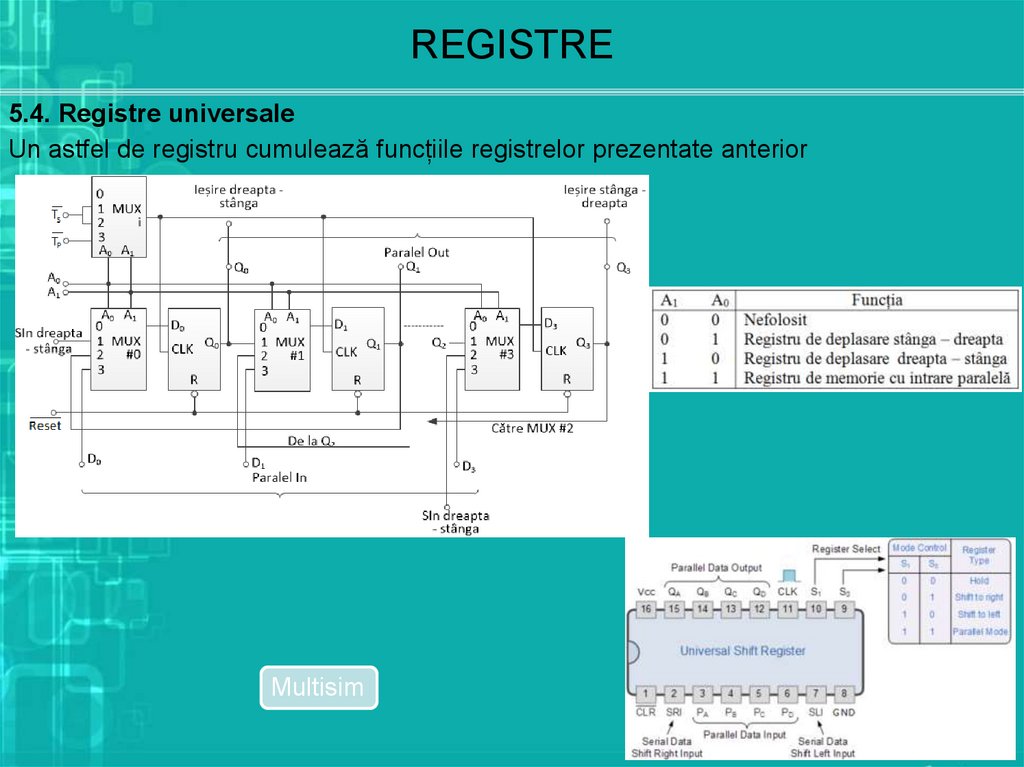
REGISTRE
5.4. Registre universale
Un astfel de registru cumulează funcțiile registrelor prezentate anterior
Multisim

83.

REGISTRE
5.5. Aplicaţii ale registrelor
5.5.1. Convertor paralel – serie
Realizează transformare unor cuvinte de cod din format paralel (ce permite accesul
simultan la toate simbolurile cuvântului) în cuvinte de cod în format serie (ce permite
accesul consecutiv la simbolurile cuvântului de cod).

84.

REGISTRE
5.5. Aplicaţii ale registrelor
5.5.2. Convertor serie – paralel
Un convertor serie – paralel transformă o succesiunea serie de simboluri (cuvânt de
cod în format serie) într-un cuvânt de cod în format paralel și schema presupune
utilizarea unui registru de tip SIPO
Ritmul în care sunt aduși biții la intrarea
serială SIn trebuie sa fie corelat cu
secvența de aplicare a impulsurilor de tact
Secvența de încărcare a registrului este
obținută prin repetarea de 8 ori a
succesiunii:
SIn (I/O2) = Di → CLK (I/O1) = 1 →
CLK (I/O1) = 0 și primul bit înscris va fi
bitul Q7.

85.

REGISTRE
5.6. Registre de deplasare cu reacție
Un astfel de registru se compune dintr-un registru de
deplasare și un circuit logic combinaţional.
După natura funcției realizată de circuitul logic
combinaţional registrele de deplasare cu reacție pot fi:
registrul de deplasare în inel, numărătorul Johnson și
generatorul de secvențe binare.
5.6.1. Numărător in inel
Multisim
5.6.2. Numărător Johnson
Multisim