Способы представления криволинейных поверхностей

1. Способы представления криволинейных поверхностей

*Способы
представления
криволинейных
поверхностей
Лектор Вишнякова И. Н.
Кафедра Компьютерных информационных технологий

2. Способы представления

*Способы представления
*В
зависимости
реалистичности:
от
степени
*поточечное представление
*каркасное представление
*в виде полигональной сетки
*реалистическое изображение:
*в аналитическом виде
*бикубические параметрические поверхности
2

3. Поточечное представление поверхности

*Поточечное представление
*
поверхности
Представление поверхности по точкам требует
знания координат каждой точки поверхности и ее цвета
и прозрачности.
*Плюсы:
* позволяет достаточно просто описывать сложные
объекты и сцены;
* простая процедура отображения сцены;
*Минусы:
* использование достаточного объема памяти;
* ограничение на разрешительную способность, точность
моделирования;
* низкая скорость создания изображения;
* проблемы при масштабировании изображения.
3

4. Каркасное представление поверхности

*Каркасное представление
поверхности
*
Каркасная модель представляет собой
каркас графического объекта, образованный
отрезками прямых линий.
*Плюсы:
*минимальные затраты оперативной памяти;
*простая процедура отображения сцены;
*Минусы:
*представление не реалистично;
*узкое назначение – представление простых
пространственных графических объектов.
4

5. Полигональное представление поверхности

*Полигональное
представление поверхности
*
Полигональная сетка – это совокупность
связанных между собой плоских
многоугольников (четырехугольников или
треугольников).
*Способы представления:
*Явное задание граней;
*Задание граней с помощью
указателей в списке
вершин;
*Явное задание ребер.
5

6. Явное задание граней

*Явное задание граней
6

7. Задание граней с помощью указателей в списке вершин

* Задание граней с помощью указателей в
списке вершин
7

8. Явное задание ребер

* Явное задание ребер
8

9. Аналитическое задание поверхности

*Аналитическое задание
поверхности
*
Для описания поверхности используются
математические формулы.
*общая форма
;
*с использованием двух функций:
*
;
* параметрическое задание функций
*
- некоторые параметры, которые
изменяются в определенном диапазоне.
9

10. Бикубическое задание кривой

*Бикубическое задание кривой
*Способы представления кривых:
*Метод Эрмита
*Метод Безье
*В-сплайн
10

11. Бикубическая кривая Эрмита

*Бикубическая кривая Эрмита
*
– крайние точки кривой;
*
– направляющие вектора в крайних точках
кривой соответственно.
*Необходимо вычислить коэффициенты
*при следующих условиях:
*
.
11

12. Вычисление коэффициентов кривой Эрмита

* Вычисление коэффициентов кривой
Эрмита
12

13. Получение матрицы Эрмита

* Получение матрицы Эрмита
13

14. Уравнения кривых Эрмита

* Уравнения кривых Эрмита
14

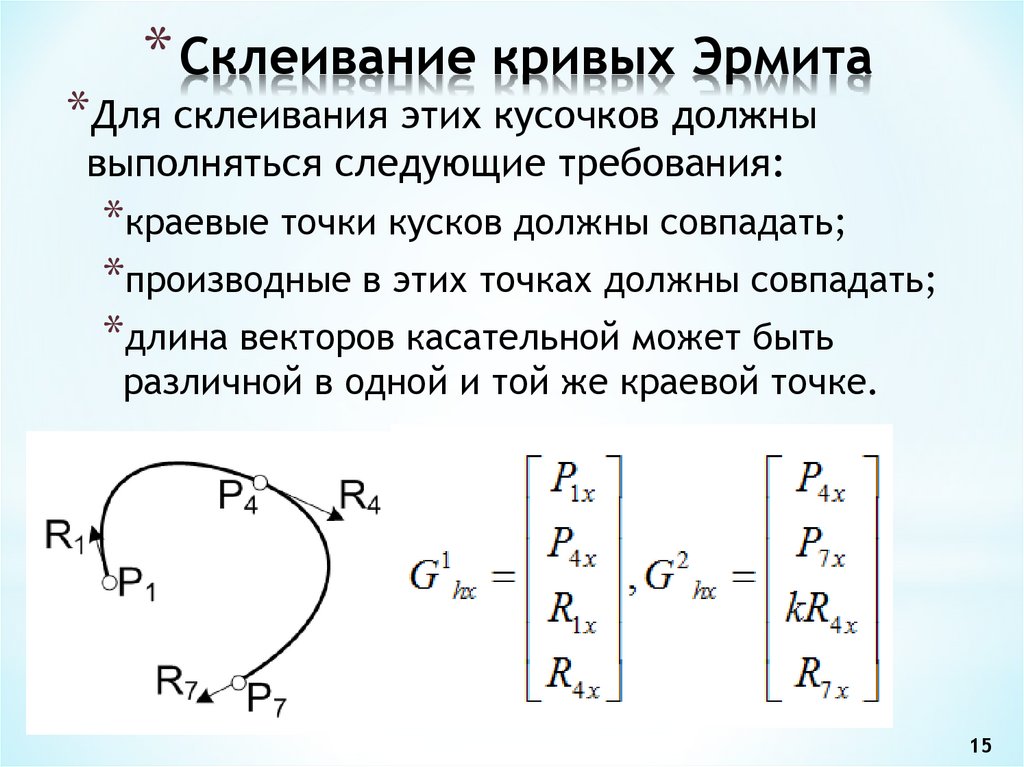
15. Склеивание кривых Эрмита

* Склеивание кривых Эрмита
*Для склеивания этих кусочков должны
выполняться следующие требования:
*краевые точки кусков должны совпадать;
*производные в этих точках должны совпадать;
*длина векторов касательной может быть
различной в одной и той же краевой точке.
15

16. Форма Эрмита

* Форма Эрмита
16

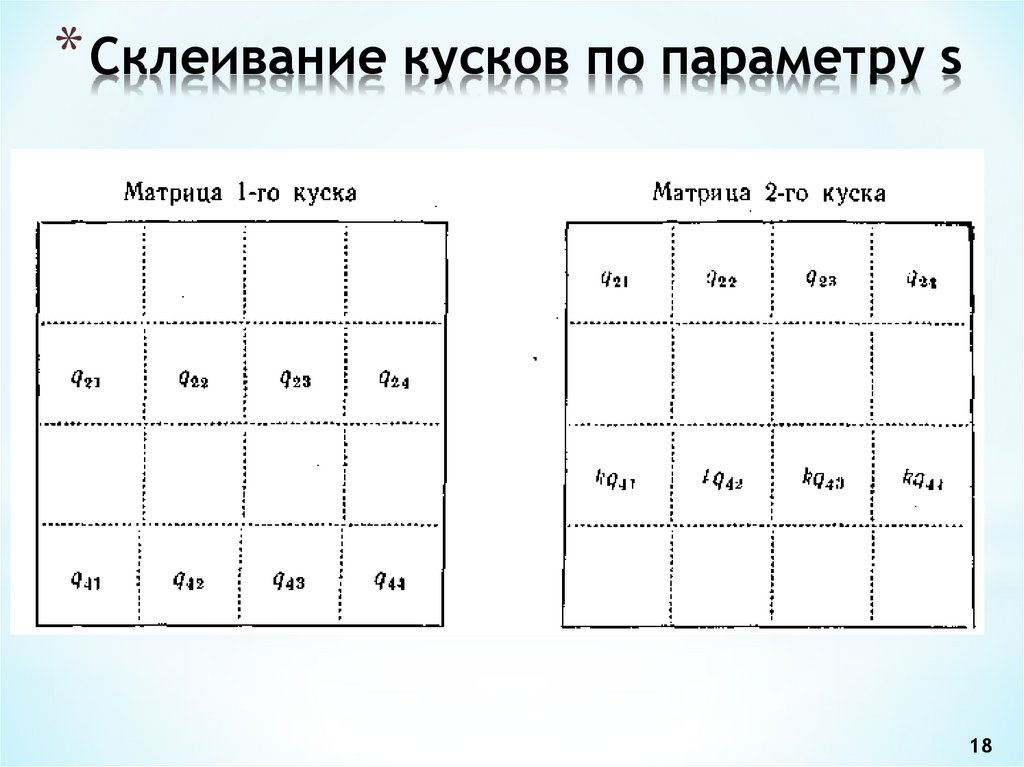
17. Склеивание кусков по параметру s

* Склеивание кусков по параметру s
17

18. Склеивание кусков по параметру s

* Склеивание кусков по параметру s
18

19. Склеивание кусков по параметру t

* Склеивание кусков по параметру t
19

20. Кривая Безье

* Кривая Безье
20

21. Представление кривой Безье

* Представление кривой Безье
*
21

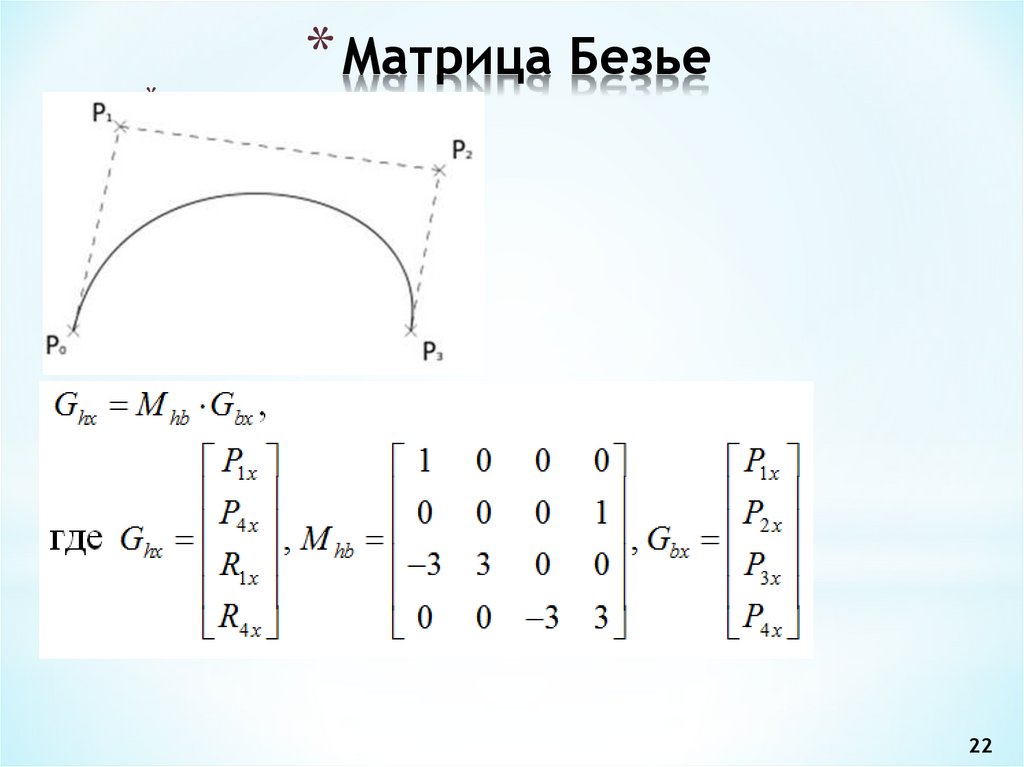
22. Матрица Безье

*
* Матрица Безье
22

23. Параметрическое представление кривой Безье

* Параметрическое представление
*
кривой Безье
23

24. Форма Безье

* Форма Безье
24

25.

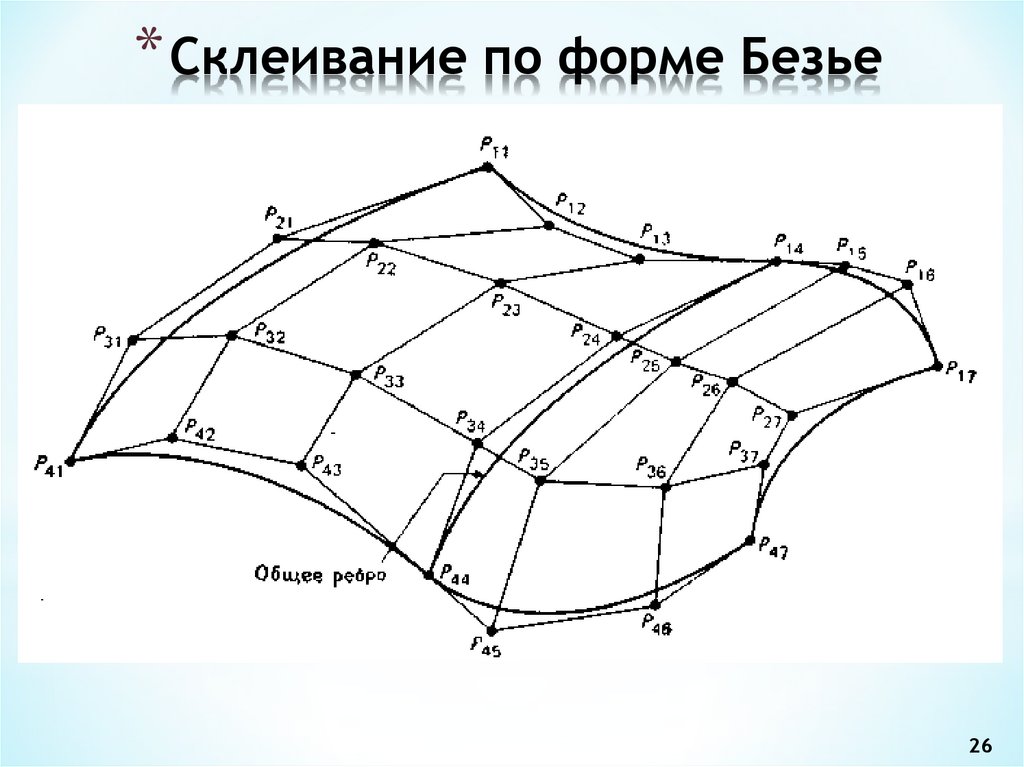
25

26. Склеивание по форме Безье

* Склеивание по форме Безье
26

27. B-сплайн

*
* B-сплайн
27

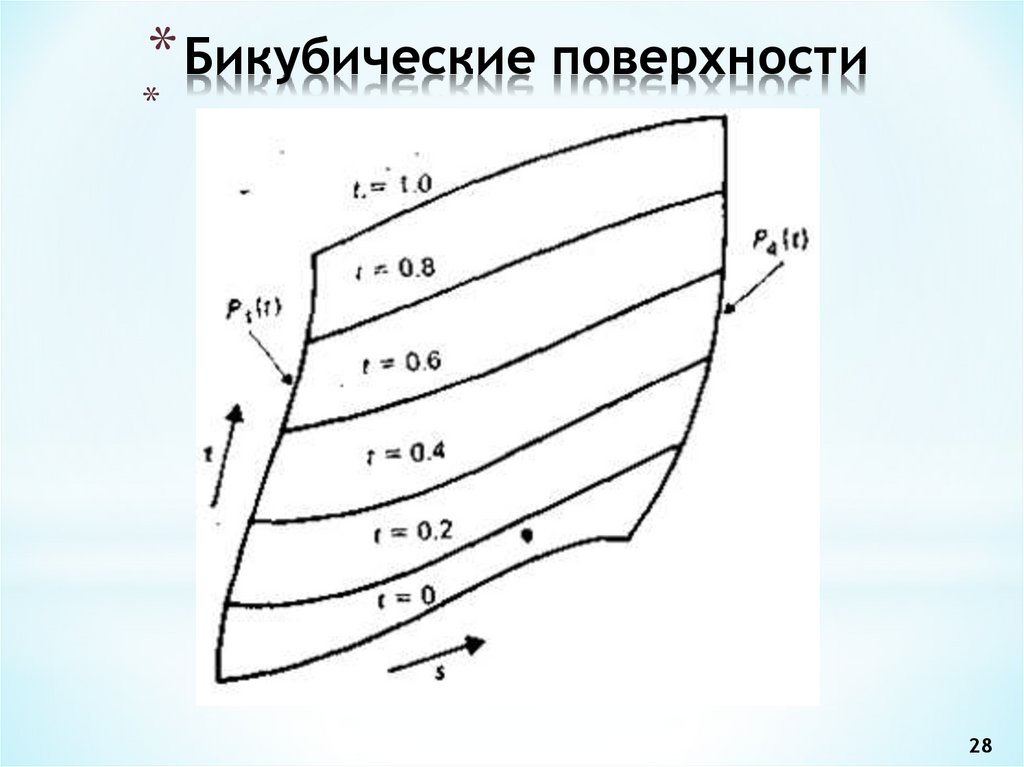
28. Бикубические поверхности

* Бикубические поверхности
*
28

29. Бикубические поверхности

* Бикубические поверхности
29

30. Форма В-сплайна

* Форма В-сплайна
30