Алгоритмы удаления скрытых линий и поверхностей

1. Алгоритмы удаления скрытых линий и поверхностей

*Алгоритмы
удаления
скрытых линий и
поверхностей
Лектор Вишнякова И. Н.
Кафедра Компьютерных информационных технологий

2. Задача удаления скрытых линий и поверхностей

*Задача удаления скрытых линий
и поверхностей
* Алгоритмы
удаления невидимых линий и поверхностей
служат для определения линий ребер, поверхностей,
которые видимы или невидимы для наблюдателя,
находящегося в заданной точке пространства.
* Невидимой будет грань, нормаль N к которой
ориентирована в ту же сторону, что и вектор R,
направленный от наблюдателя к объекту.
* Иными словами, для невидимых граней скалярное
произведение данных векторов положительно: NR> 0.
2

3. Нормали тетраэдра

*
3

4. Классификация алгоритмов по пространству

*Классификация алгоритмов по
пространству
*Выделяют три класса алгоритмов удаления
невидимых линий или поверхностей:
*Алгоритмы, работающие в объектном
пространстве (3D).
*Алгоритмы, работающие в пространстве
изображения (экрана) (2D).
*Алгоритмы, формирующие список приоритетов.
4

5. Алгоритмы, работающие с объектом в пространстве

*Алгоритмы, работающие с
объектом в пространстве
* Работают в физической СК, в которой описаны эти объекты.
* Плюсы:
* Точные расчеты, ограниченные только точностью вычислений.
* Полученные изображения можно свободно увеличивать во
много раз.
* Объем вычислений растет теоретически, как квадрат числа
объектов (n2).
* К таким алгоритма относятся:
* Робертса (1963) ;
* Вейлера-Айзертона (1977) ;
* BSP-деревьев (1969-91);
* Октодеревьев (1982).
5

6. Алгоритмы, работающие в пространстве экрана

*Алгоритмы, работающие в
пространстве экрана
*Работают в СК изображения (экрана).
*Точность вычислений ограничена разрешением
экрана.
*Полученные изображения плохо масштабируются –
теряется качество.
*Объем вычислений растет теоретически, как n*N (n –
количество объектов, N – количество пикселей на
экране).
*К таким алгоритма относятся:
* Z-буфера (1974);
А-буфера;
* Плавающего горизонта; «Художника»;
* Варнока (1968) ;
Построчного сканирования (1967) ;
* Трассировки лучей (1968).
6

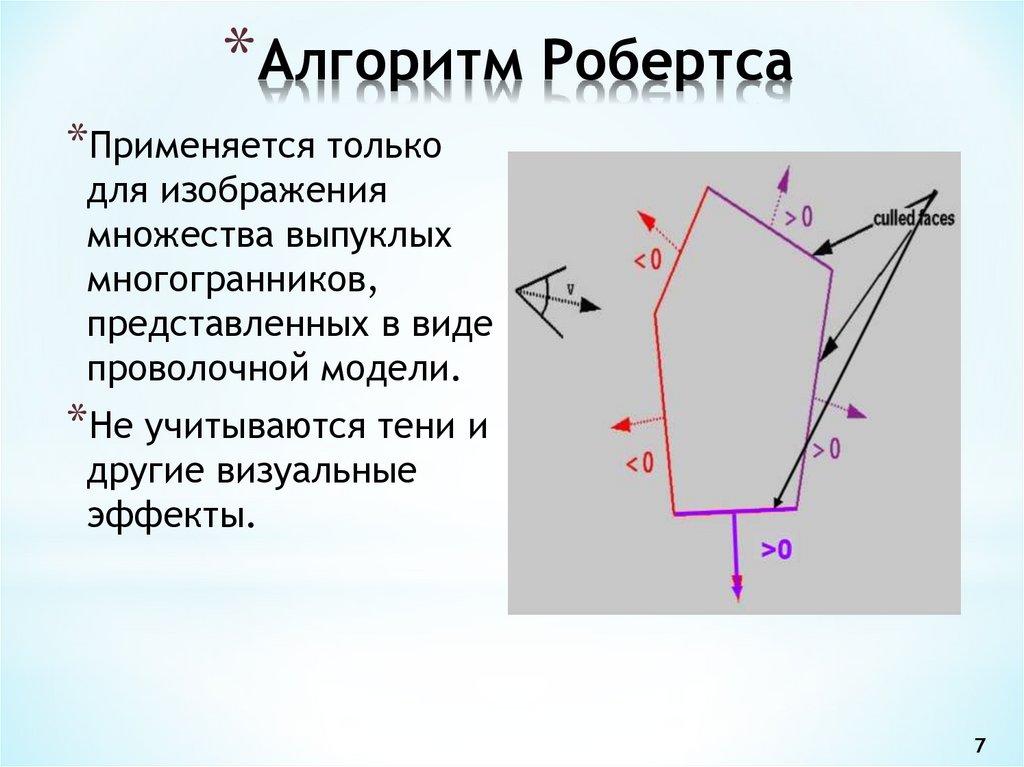
7. Алгоритм Робертса

*Алгоритм Робертса
*Применяется только
для изображения
множества выпуклых
многогранников,
представленных в виде
проволочной модели.
*Не учитываются тени и
другие визуальные
эффекты.
7

8. Алгоритм Робертса

*Алгоритм Робертса
*Идея алгоритма:
*1. Удаляются из каждого объекта те ребра или
грани, которые скрываются самим объектом.
*2. Каждое из видимых ребер каждого объекта
сравнивается с каждым из оставшихся объектов
для определения того, какая его часть или
части, если таковые есть, скрываются этими
объектами.
8

9. Алгоритм Робертса (1 этап)

*Алгоритм Робертса (1 этап)
* Для каждого объекта сцены:
Вычислить уравнение плоскости для каждой грани объекта.
Вычислить проекции граней.
Вычислить и запомнить габариты прямоугольника,
описывающего проекцию объекта: Xmax, Xmin, Ymax, Ymin
Определить не лицевые плоскости:
oВычислить скалярное произведение вектора R (нормаль от
наблюдателя к грани объекта) и вектора N (нормаль грани
объекта).
oЕсли RN>0 – грань невидима.
oУдалить весь описывающий многоугольник, лежащий в
данной плоскости.
* Если в сцене лишь 1 объект – алгоритм завершён, иначе – 2й этап.
9

10. Алгоритм Робертса (2 этап)

*Алгоритм Робертса (2 этап)
* Выполняется проверка: существуют ли такие отрезки,
которые перекрываются другими объектами на экране. Для
этого каждый оставшийся отрезок или ребро нужно
сравнить с другими объектами сцены или картинки.
* Сформировать список «приоритета» объектов,
упорядоченных по Z координате.
* Возможны следующие случаи:
Грань не закрывает ребро. Ребро остается в списке ребер.
Грань полностью закрывает ребро. Ребро удаляется из
списка рассматриваемых ребер.
Грань частично закрывает ребро. В этом случае ребро
разбивается на несколько частей. Само ребро удаляется из
списка рассматриваемых ребер, но в список проверяемых
ребер добавляются те его части, которые данной гранью не
закрываются.
10

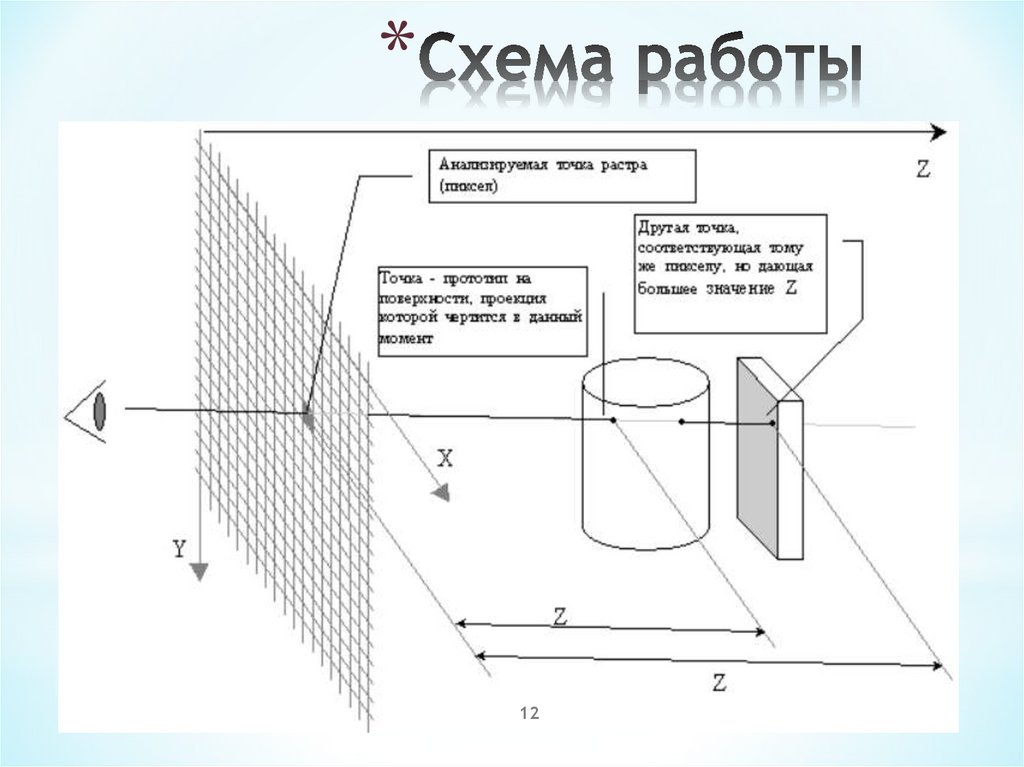
11. Алгоритм Z-буфера

*Алгоритм Z-буфера
* Работает алгоритм в пространстве изображения.
* z-буфер - это отдельный буфер глубины, используемый для
запоминания координаты z или глубины каждого видимого
пиксела в пространстве изображения.
* В процессе работы глубина или значение z каждого нового
пиксела, который нужно занести в буфер кадра, сравнивается
с глубиной того пиксела, который уже занесен в z-буфер.
* Если это сравнение показывает, что новый пиксел расположен
впереди пиксела, находящегося в буфере кадра, то новый
пиксел заносится в этот буфер и, кроме того, производится
корректировка z-буфера новым значением z.
* Если же сравнение дает противоположный результат, то
никаких действий не производится.
* По сути, алгоритм является поиском по х и у наибольшего
значения функции z (х, у).
11

12. Схема работы

*
12

13. Описание алгоритма Z-буфера

*Описание алгоритма Z-буфера
*1.
Заполнить буфер кадра фоновым значением
интенсивности или цвета.
*2.
*3.
Заполнить z-буфер минимальным значением z.
Преобразовать каждый многоугольник в растровую
форму в произвольном порядке.
*4.
Для каждого Пиксел(x,y) в многоугольнике
вычислить его глубину z(x,y).
*5.
Сравнить глубину z(х,у) со значением Zбуфер(х,у),
хранящимся в z-буфере в этой же позиции.
*Если z(х,у) > Zбуфер (х,у), то записать атрибут этого
многоугольника (интенсивность, цвет и т. п.) в буфер
кадра и заменить Zбуфер(х,у) на z(х,у).
*В противном случае никаких действий не производить.
13

14. Недостатки алгоритма

*
* Основной недостаток алгоритма с Z-буфером - большой объем
требуемой памяти. Если сцена подвергается видовому
преобразованию и отсекается до фиксированного диапазона
координат z значений, то можно использовать z-буфер с
фиксированной точностью. Информацию о глубине нужно
обрабатывать с большей точностью, чем координатную
информацию на плоскости (x, y); обычно бывает достаточно 20
бит. Буфер кадра размером 512 * 512 * 24 бит в комбинации с
z-буфером размером 512 * 512 * 20 бит требует почти 1.5
мегабайт памяти.
* Так как пиксели в буфер заносятся в произвольном порядке,
то возникают трудности с реализацией эффектов прозрачности
или просвечивания.
14

15. Преимущества

*
*Прост в аппаратной реализации
*Разнородность использующихся примитивов – не
ограничиваемся только полигонами.
*Нелимитированная возможная сложность сцены.
*Отсутствие необходимости вычисления
пересечений объектов сцены друг с другом.
15

16. Алгоритм A-буфера

*
* Алгоритм является расширением
метода буфера глубины (в
названии использована
противоположная от Z буква
алфавита). Данное расширение
предназначено специально для
обеспечения эффектов
усреднения по области,
прозрачности, оптимизации
наложения полигонов. Область
буфера в алгоритме называется
буфером накопления, так как в
ней в дополнение к значениям
глубин хранятся различные
16
данные о поверхности.

17. Описание работы

*
* Каждая позиция в А-буфере имеет два поля.
- поле глубины:
здесь хранится действительное значение (положительное,
отрицательное или ноль). - поле данных о поверхности: здесь
находятся данные о поверхности или указатель.
* Данные по поверхности включают следующие поля:
- значения интенсивностей RGB-компонентов
- параметр непрозрачности (процент прозрачности)
- другие параметры, требуемые для визуализации поверхности.
Схема работы алгоритма аналогична Z-буферу. При реализации
прозрачности алгоритм учитывает параметры прозрачности
каждой поверхности и её процент охвата каждого пикселя,
соответственно цвет каждого пикселя итогового изображения
получается как среднее вкладов перекрывающихся
поверхностей.
17

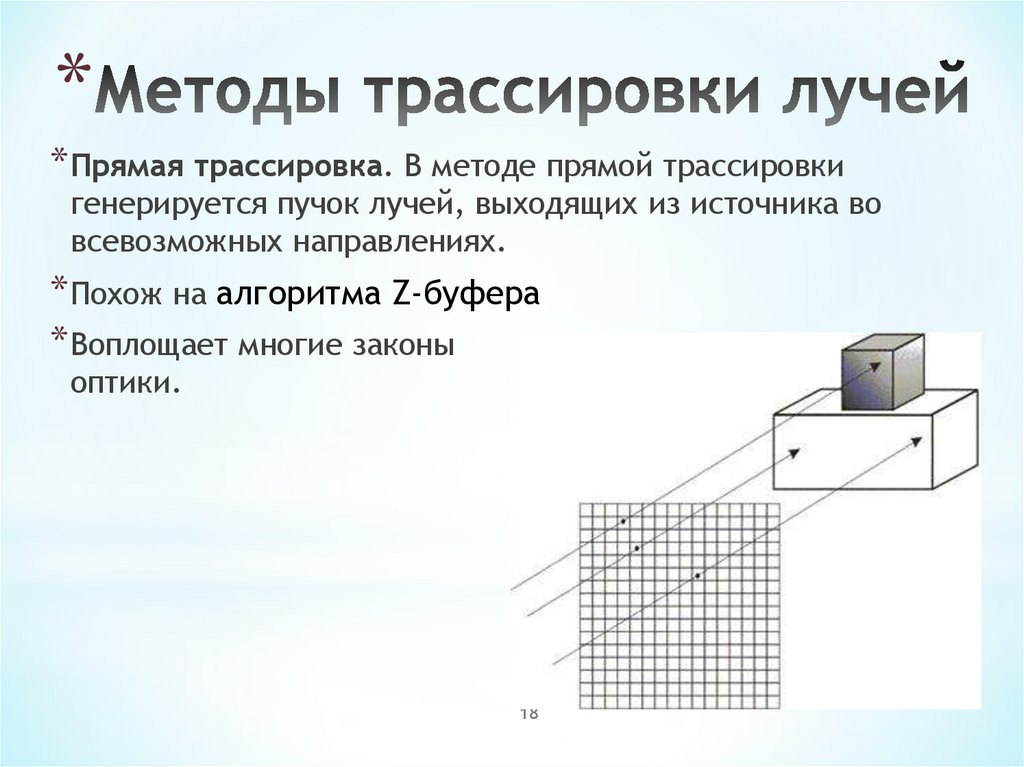
18. Методы трассировки лучей

*
* Прямая трассировка. В методе прямой трассировки
генерируется пучок лучей, выходящих из источника во
всевозможных направлениях.
* Похож на алгоритма Z-буфера
* Воплощает многие законы
оптики.
18

19. Алгоритм художника

*Алгоритм художника
*Многоугольники сначала упорядочиваются в
направлении от заднего плана к переднему.
*В случае, когда пары многоугольников не
удается достаточно просто упорядочить, они
подразделяются на части до тех пор, пока
получившиеся части не позволят это сделать.
*Характеристика удаленности для грани ABC это среднее значение z,
mid_z = (A.z+B.z+C.z)/3.
19

20. Недостатки

*
* при некотором расположении
граней этот алгоритм вообще не
может дать правильного
результата
* при использовании этого
алгоритма выводятся вообще все
грани сцены, и при большом
количестве загораживающих
друг друга граней, большая часть
времени тратится на вывод
невидимых в конечном итоге
частей
20

21. Алгоритм Варнока

*Алгоритм Варнока
*Работает в пространстве изображения.
*В пространстве изображения рассматривается
окно и решается вопрос о том, пусто ли оно,
или его содержимое достаточно просто для
визуализации.
*Если это не так, то окно разбивается на
фрагменты до тех пор, пока содержимое
фрагмента не станет достаточно простым для
визуализации или его размер не достигнет
требуемого предела разрешения.
21

22. Алгоритм Варнока

*Алгоритм Варнока
*1. Проекция грани полностью накрывает область (рис. d);
*2. Проекция грани пересекает область, но не
содержится в ней полностью (рис. с);
*3.
Проекция грани целиком содержится внутри области
(рис. b);
*4.
Проекция грани не имеет общих внутренних точек с
рассматриваемой областью (рис. a).
22

23. Алгоритм Варнока

*Алгоритм Варнока
* Сравнивая область с проекциями всех граней, можно
выделить случаи, когда изображение, получающееся в
рассматриваемой области, определяется сразу:
Проекция ни одной грани не попадает в область.
Проекция только одной грани содержится в области или
пересекает область. В этом случае проекции грани разбивают
всю область на две части, одна из которых соответствует этой
проекции.
Существует грань, проекция которой полностью накрывает
данную область, и эта грань расположена к картинной
плоскости ближе, чем все остальные грани, проекции которых
пересекают данную область. В данном случае область
соответствует этой грани.
* Если ни один из рассмотренных трех случаев не имеет
места, то снова разбиваем область на четыре равные части
и проверяем выполнение этих условий для каждой из
23
частей и т.д.

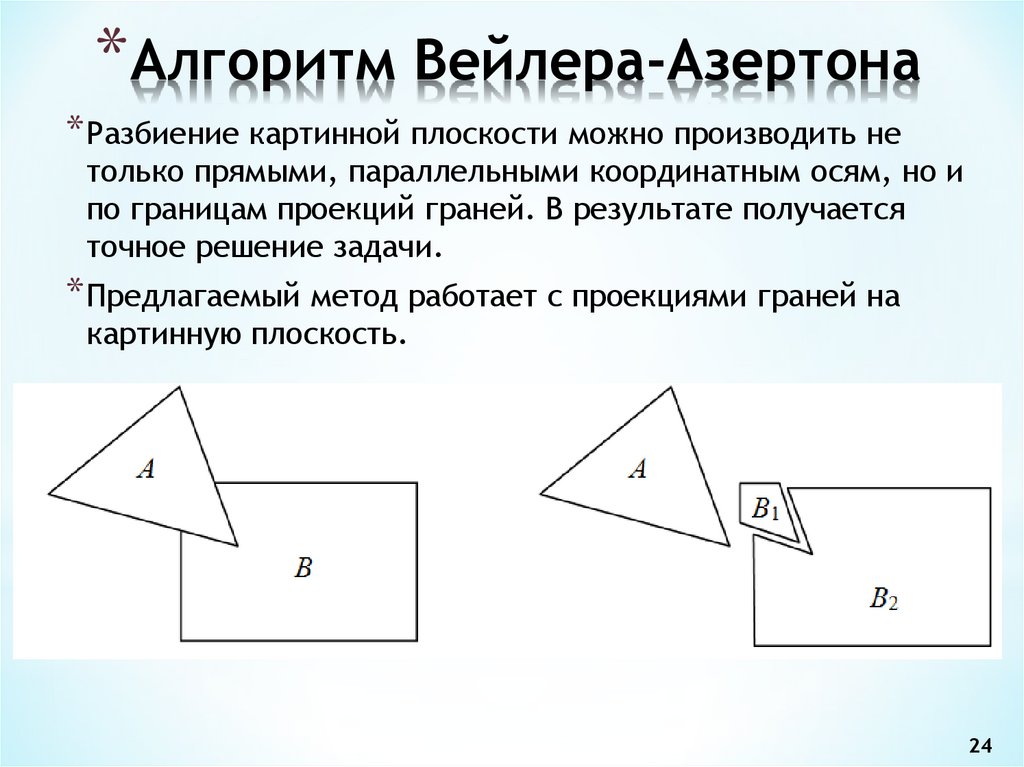
24. Алгоритм Вейлера-Азертона

*Алгоритм Вейлера-Азертона
* Разбиение картинной плоскости можно производить не
только прямыми, параллельными координатным осям, но и
по границам проекций граней. В результате получается
точное решение задачи.
* Предлагаемый метод работает с проекциями граней на
картинную плоскость.
24

25. Алгоритм Вейлера-Азертона

*Алгоритм Вейлера-Азертона
* 1. Сортировка всех граней по глубине (front-to-back).
* 2. Из списка оставшихся граней берется ближайшая грань A и все
остальные грани обрезаются по этой грани.
* Если проекция грани B пересекает проекцию грани A, то грань
B разбивается на части так, что каждая часть либо содержится
в грани A, либо не имеет с ней общих внутренних точек.
* Таким образом, получаются два множества граней: Fin – грани,
проекции которых содержатся в проекции грани A (сюда входит
и сама грань A), и Fout – грани, проекции которых не имеют
общих внутренних точек с проекцией грани A.
* Множество Fin обычно называют множеством граней,
внутренних по отношению к A.
* 3. Если во множестве Fin
есть грани, лежащие к наблюдателю
ближе, чем сама грань A, то каждая такая грань используется для
разбиения всех граней из множества Fin (включая грань A).
* 4. Из множества оставшихся граней Fout берется очередная грань
и процедура повторяется, начиная с п.2.
25