Возрастание и убывание (монотонность) функции

1.

Тема урока № 65
Возрастание и убывание
(монотонность) функции
Цели обучения:
10.3.1.15 - знать и применять необходимое и
достаточное условие возрастания (убывания)
функции на интервале

2.

Критерии успеха
– знает необходимое и достаточное условия
возрастания (убывания) функции на
интервале
– умеет определять промежутки
возрастания и убывания функции
различными способами

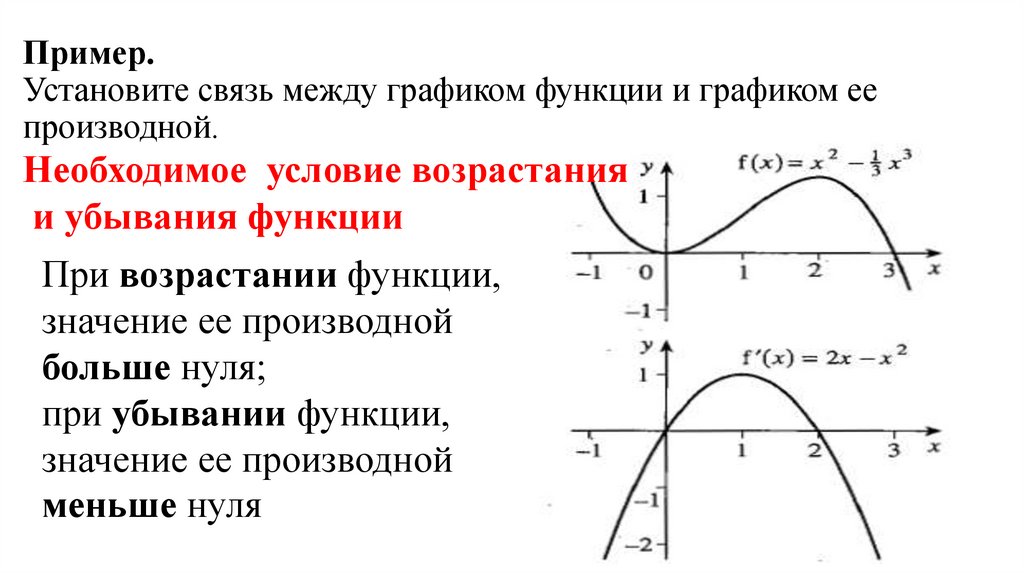
3. Пример. Установите связь между графиком функции и графиком ее производной.

Пример.
Установите связь между графиком функции и графиком ее
производной.
Необходимое условие возрастания
и убывания функции
При возрастании функции,
значение ее производной
больше нуля;
при убывании функции,
значение ее производной
меньше нуля

4.

Достаточное условие возрастания и убывания функции
Если производная некоторой непрерывной функции f(x)
на некотором промежутке положительна (f '(x)>0), то на
этом промежутке функция возрастает.
Если производная некоторой непрерывной функции f(x)
на некотором промежутке отрицательна (f '(x)<0), то на
этом промежутке функция убывает.

5. Алгоритм нахождения промежутков монотонности

1. Найти область определения функции.
2. Найти производную функции.
3. Решить неравенства f/(x) > 0 или f/(x) < 0.
4. Записать промежутки возрастания и убывания функции.

6.

Найдите промежутки возрастания и убывания функции:
1) у 3 0,5 х
Дескрипторы:
Находит производную функции
Решает соответствующее неравенство
Записывает в ответе промежутки монотонности

7.

Найдите промежутки возрастания и убывания функции:
1) у 2 х 4 х 5;
2
Дескрипторы:
Находит производную функции
Решает соответствующее неравенство
Записывает в ответе промежутки монотонности
2) у х 2 х 3 ;

8.

Найдите промежутки возрастания и убывания функции:
2) у 1 2 х 3 2х ;
Дескрипторы:
Находит производную функции
Решает соответствующее неравенство
Записывает в ответе промежутки монотонности
х 4
3) у
4 х

9. Рефлексия