Машина Тьюринга

1.

ДМ2 Л15 Машина Тьюринга
1. Описание машины Тьюринга
Машина Тьюринга (МТ) состоит из двух частей – ленты и автомата
Лента используется для хранения информации. Она бесконечна в обе стороны и разбита на
клетки, которые никак не нумеруются и не именуются. Содержимое клетки может меняться
– в неё можно записать другой символ или стереть находящийся там символ. Пустое содержимое клетки будем обозначать знаком Λ («лямбда») - изображение ленты справа, такое же,
как и слева. Операцию стирания символа в клетке это запись в эту клетку Λ, Автомат – это
часть МТ. В каждый момент он размещается под одной из клеток ленты и видит её содержимое; это видимая клетка, а находящийся в ней символ – видимый символ; содержимое соседних и других клеток автомат не видит. В каждый момент автомат находится в одном из
состояний: q1, q2, … Находясь в некотором состоянии, автомат выполняет определённую
операцию ( перемещение по ленте, запись символа в клетку). Пара из видимого символа S и
текущего состояния автомата q называется конфигурацией: <S, q>.
Автомат может выполнять три элементарных действия:
1) записывать в видимую клетку новый символ
2) сдвигаться на одну клетку влево или вправо
3) переходить в новое состояние.

2.

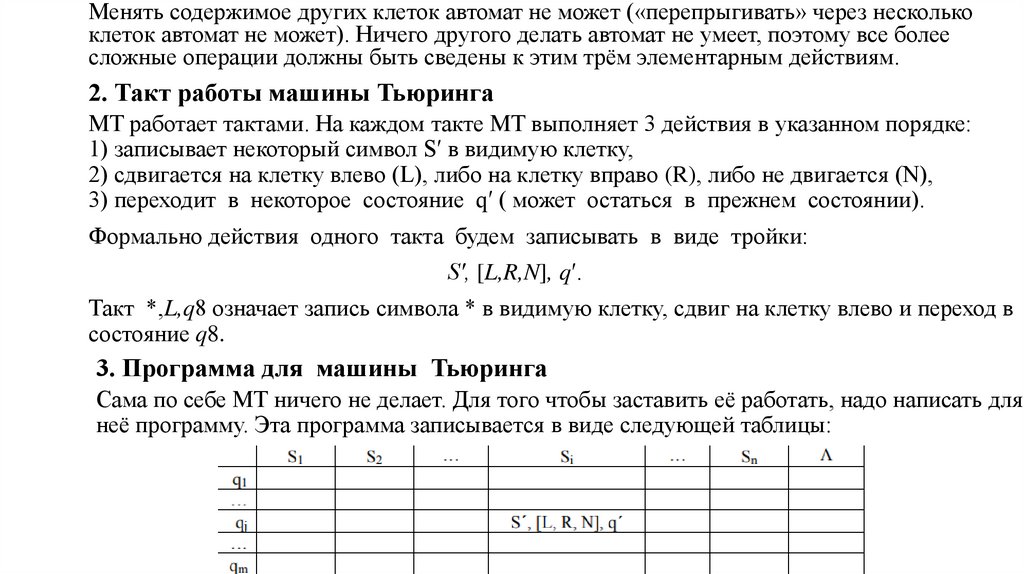
Менять содержимое других клеток автомат не может («перепрыгивать» через несколько
клеток автомат не может). Ничего другого делать автомат не умеет, поэтому все более
сложные операции должны быть сведены к этим трём элементарным действиям.
2. Такт работы машины Тьюринга
МТ работает тактами. На каждом такте МТ выполняет 3 действия в указанном порядке:
1) записывает некоторый символ S′ в видимую клетку,
2) сдвигается на клетку влево (L), либо на клетку вправо (R), либо не двигается (N),
3) переходит в некоторое состояние q′ ( может остаться в прежнем состоянии).
Формально действия одного такта будем записывать в виде тройки:
S′, [L,R,N], q′.
Такт *,L,q8 означает запись символа * в видимую клетку, сдвиг на клетку влево и переход в
состояние q8.
3. Программа для машины Тьюринга
Сама по себе МТ ничего не делает. Для того чтобы заставить её работать, надо написать для
неё программу. Эта программа записывается в виде следующей таблицы:

3.

Таблица определяет действия МТ при всех возможных конфигурациях и полностью задаёт
поведение МТ. Описать алгоритм в виде МТ – значит предъявить такую таблицу.
До выполнения программы необходимо
1) записать на ленту входное слово – конечную последовательность символов, записанных в
соседних клетках ленты; внутри входного слова пустых клеток быть не должно, а слева и
справа от него должны быть только пустые клетки.
2) установить автомат в состояние q1 и разместить его под 1-м символом входного слова:
Выполнение программы начинается с отыскания ячейки на пересечении 1-й строки и столбца, соответствующего 1-му символу входного слова, далее выполняется такт, указанный в
этой ячейке. В результате автомат окажется в новой конфигурации. Теперь аналогичные
действия повторяются для новой конфигурации.
Когда завершается выполнение программы? Введём понятие такта останова – такта,
который ничего не меняет: автомат записывает в видимую клетку символ, что был в ней
раньше, не сдвигается и остается в прежнем состоянии, т.е. это такт S,N,q, попав на который
МТ завершает свою работу.

4.

Возможны два исхода работы МТ над входным словом:
1) МТ попадает на такт останова – говорят, что МТ применима к входному слову. Слово,
которое получено на ленте, считается выходным словом, т.е. результатом работы МТ,
ответом. В момент останова должны быть выполнены следующие условия:
– внутри выходного слова не должно быть пустых клеток (во время выполнения программы
внутри слова пустые клетки допускаются);
– автомат обязан остановиться под одним из символов выходного слова.
2) зацикливание – МТ никогда не попадает на такт останова (например, автомат на
каждом шаге сдвигается вправо) – говорят, что МТ неприменима к входному слову.
Отметим, что МТ может быть применима к одним входным словам (т.е. останавливаться)
и неприменима к другим (т.е. зацикливаться). Т.е. применимость зависит не только от
алгоритма, но и от входного слова.
4. Соглашения о записи
1) Если в такте не меняется видимый символ, или автомат не сдвигается, или не меняется
состояние автомата, то в соответствующей позиции такта ничего не пишется. Например, при
конфигурации <a, q1> следующие записи тактов эквивалентны:
a,R,q3 ≡ ,R,
b,N,q2 ≡ b, ,q2
a,L,q1 ≡ ,L,
a,N,q1 ≡
, ,
(такт останова)

5.

2) Если надо указать, что после выполнения некоторого такта МТ должна остановиться, то в
третьей позиции этого такта будем писать знак «!». Например, такт b,L,! : запись символа b в
видимую клетку ленты, сдвиг влево и останов.
Формально можно считать, что в программе МТ имеется состояние с названием !, во всех
ячейках которого записаны такты останова. При этом, однако, такую строку явно не
выписывают, а лишь подразумевают.
3) Если заранее известно, что в процессе выполнения программы не может появиться
некоторая конфигурация, тогда, чтобы подчеркнуть это явно, в соответствующей ячейке
ставится крестик.
Буквой Р будем обозначать входное слово. Буквой А будем обозначать алфавит входного
слова, т.е. набор тех символов, из которых только и может состоять Р (в промежуточных и
выходном словах могут появляться и другие символы).
5. Примеры
Пример 1.
А={0,1,2,3,4,5,6,7,8,9}. Р – непустое слово. Получить на ленте запись числа Р+1.
Решение.
1. Перегнать автомат под последнюю цифру числа.
2. Если это цифра от 0 до 8, то заменить её цифрой на 1 больше и остановиться; например:

6.

3. Если это цифра 9, тогда заменить её на 0 и сдвинуть автомат к предыдущей цифре, после
чего таким же способом увеличить на 1 эту предпоследнюю цифру; например:
4. В Р только девятки (99). Тогда автомат будет сдвигаться влево до пустой клетки, заменяя
девятки на нули. В эту пустую клетку надо записать 1 и остановиться (ответом будет 100):
В полной записи программа для МТ имеет вид
В сокращённой

7.

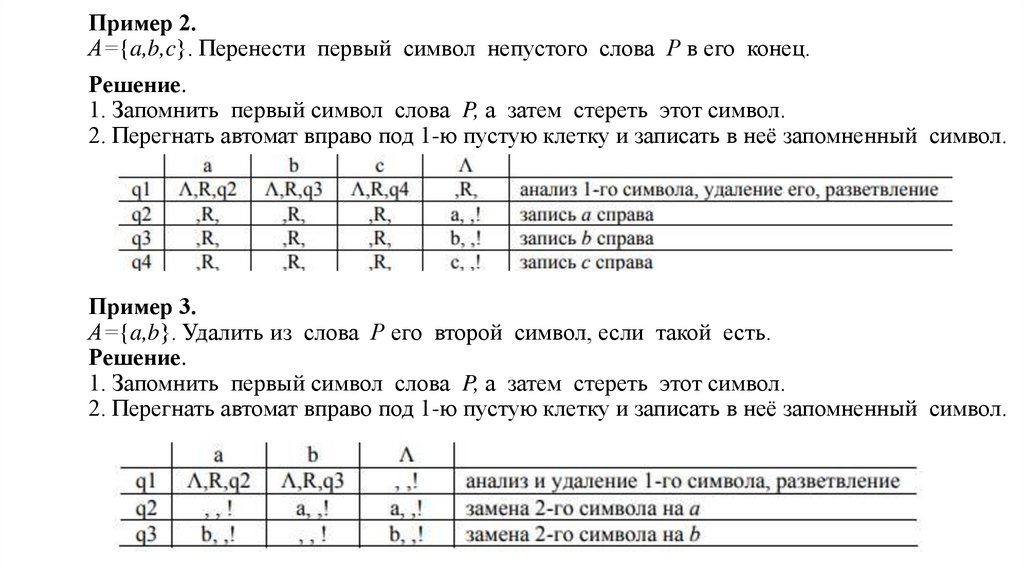
Пример 2.
А={a,b,c}. Перенести первый символ непустого слова Р в его конец.
Решение.
1. Запомнить первый символ слова P, а затем стереть этот символ.
2. Перегнать автомат вправо под 1-ю пустую клетку и записать в неё запомненный символ.
Пример 3.
А={a,b}. Удалить из слова Р его второй символ, если такой есть.
Решение.
1. Запомнить первый символ слова P, а затем стереть этот символ.
2. Перегнать автомат вправо под 1-ю пустую клетку и записать в неё запомненный символ.

8.

Пример 4.
А={a,b,c}. Если первый и последний символы (непустого) слова Р одинаковы, тогда это
слово не менять, а иначе заменить его на пустое слово..
Решение.
1. Запомнить первый символ входного слова, не стирая его.
2. Переместить автомат под последний символ и сравнить его с запомненным. Если
они равны, то больше ничего не делать.
3. В противном случае уничтожить всё входное слово..

9.

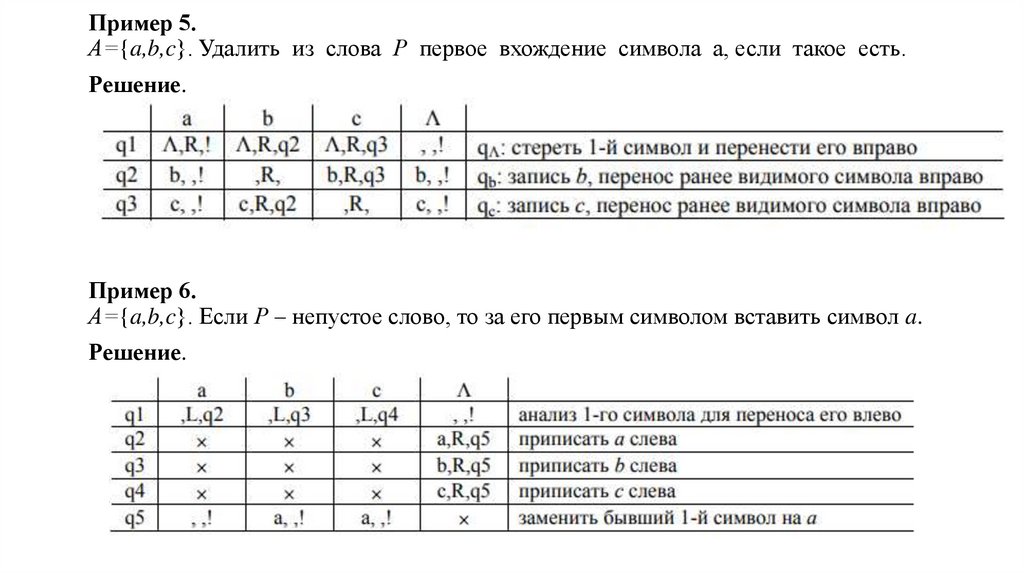
Пример 5.
А={a,b,c}. Удалить из слова Р первое вхождение символа a, если такое есть.
Решение.
Пример 6.
А={a,b,c}. Если Р – непустое слово, то за его первым символом вставить символ a.
Решение.

10.

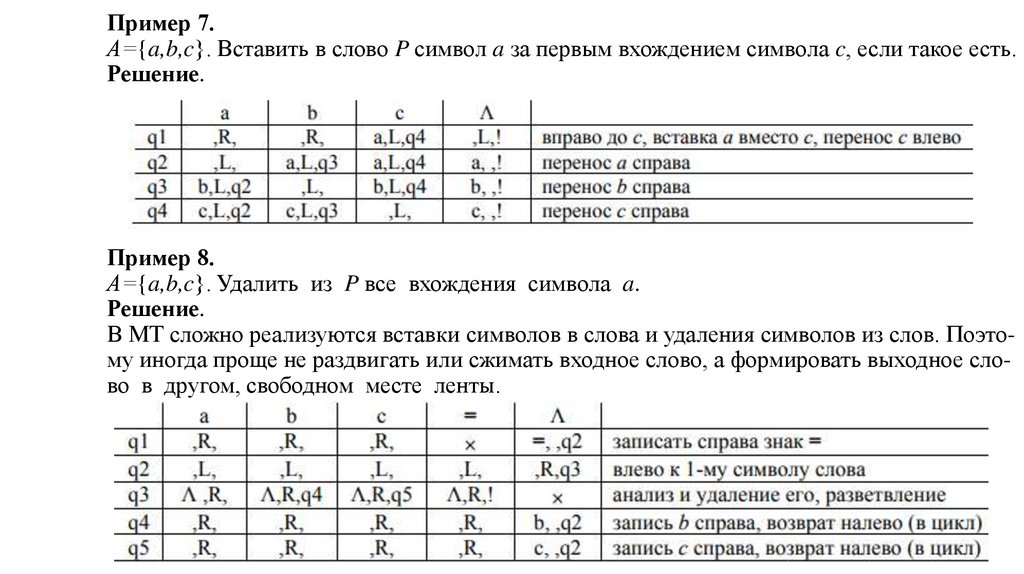
Пример 7.
А={a,b,c}. Вставить в слово P символ a за первым вхождением символа c, если такое есть.
Решение.
Пример 8.
А={a,b,c}. Удалить из P все вхождения символа a.
Решение.
В МТ сложно реализуются вставки символов в слова и удаления символов из слов. Поэтому иногда проще не раздвигать или сжимать входное слово, а формировать выходное слово в другом, свободном месте ленты.