Похожие презентации:
Конус. Определение конуса
1.
КОНУСP
F
x
2.
Конус в переводе с греческого «konos»означает «сосновая шишка».
С конусом
древности.
люди
знакомы
с
глубокой
Много сделала для геометрии
Платона (428–348 гг. до н. э.).
школа
Школе Платона, в частности, принадлежит:
а)
исследование
свойств
призмы,
пирамиды, цилиндра и конуса;
б) изучение конических сечений.
3.
Большой трактат о конических сеченияхбыл написан Аполлонием Пергским–
учеником
Евклида,
который
создал
великий труд из 15 книг под названием
«Начала». Эти книги издаются и по сей
день, а в школах Англии по ним учатся до
сих пор.
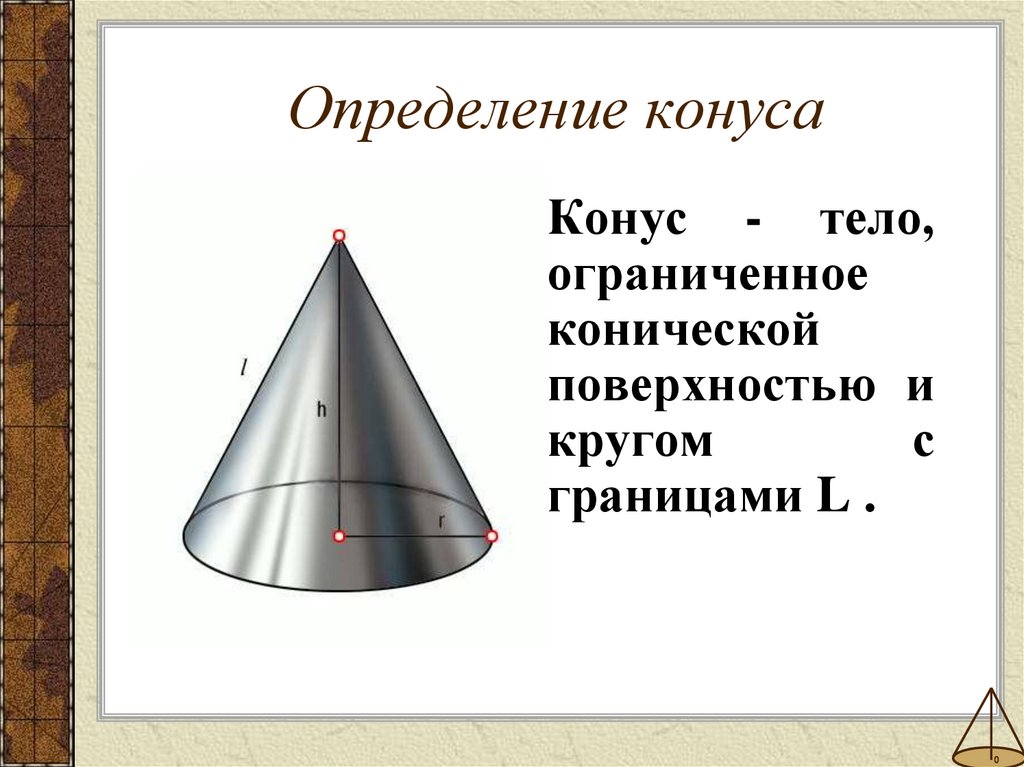
4. Определение конуса
Конус - тело,ограниченное
конической
поверхностью и
кругом
с
границами L .
5.
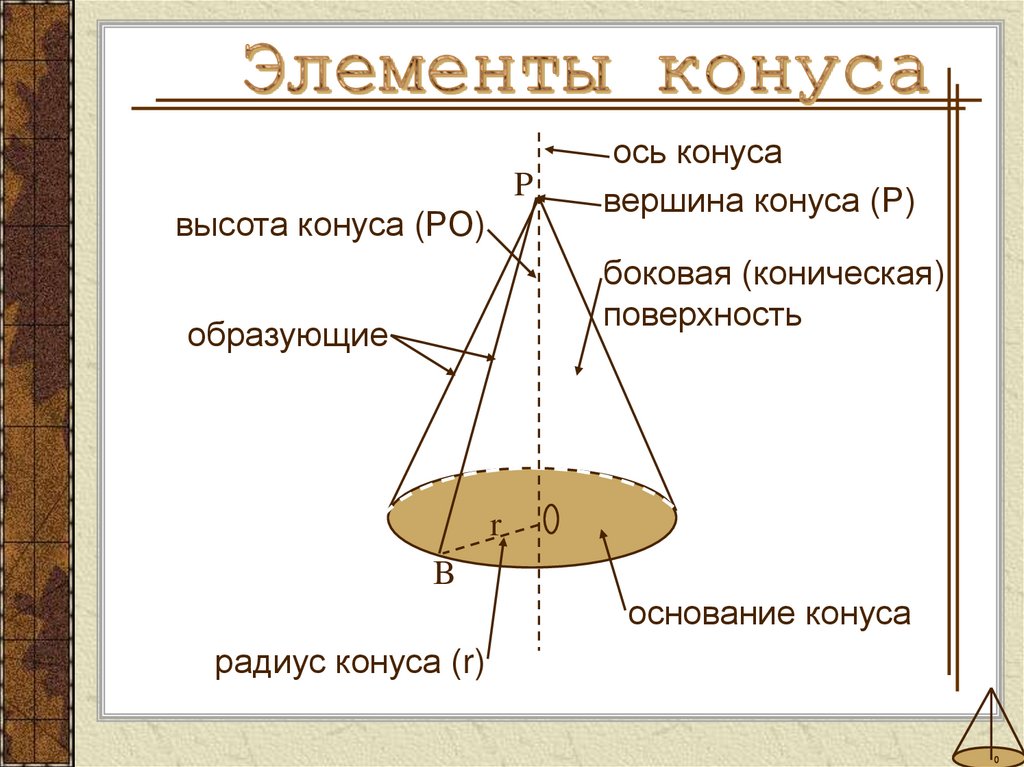
Pвысота конуса (РО)
ось конуса
вершина конуса (Р)
боковая (коническая)
поверхность
образующие
r
B
основание конуса
радиус конуса (r)
6. Получение конуса
АПолучение конуса
Вращаем
прямоугольный
треугольник вокруг
катета.
В
С
С2
С1
7.
ОСЕВОЕ СЕЧЕНИЕВ сечении равнобедренный
треугольник, основание которого
диаметр основания конуса, а
боковые стороны – образующие
конуса.
СЕЧЕНИЕ, ПЕРПЕНДИКУЛЯРНОЕ
ОСИ КОНУСА
Сечение, перпендикулярное к
оси конуса представляет собой
круг,
секущая
плоскость
перпендикулярна оси конуса.
РО1М1 ~ РОМ
r1 = РО1/РО*r
8.
Рис.1эллипс
Рис.2
парабола
Рис.3
гипербола
9.
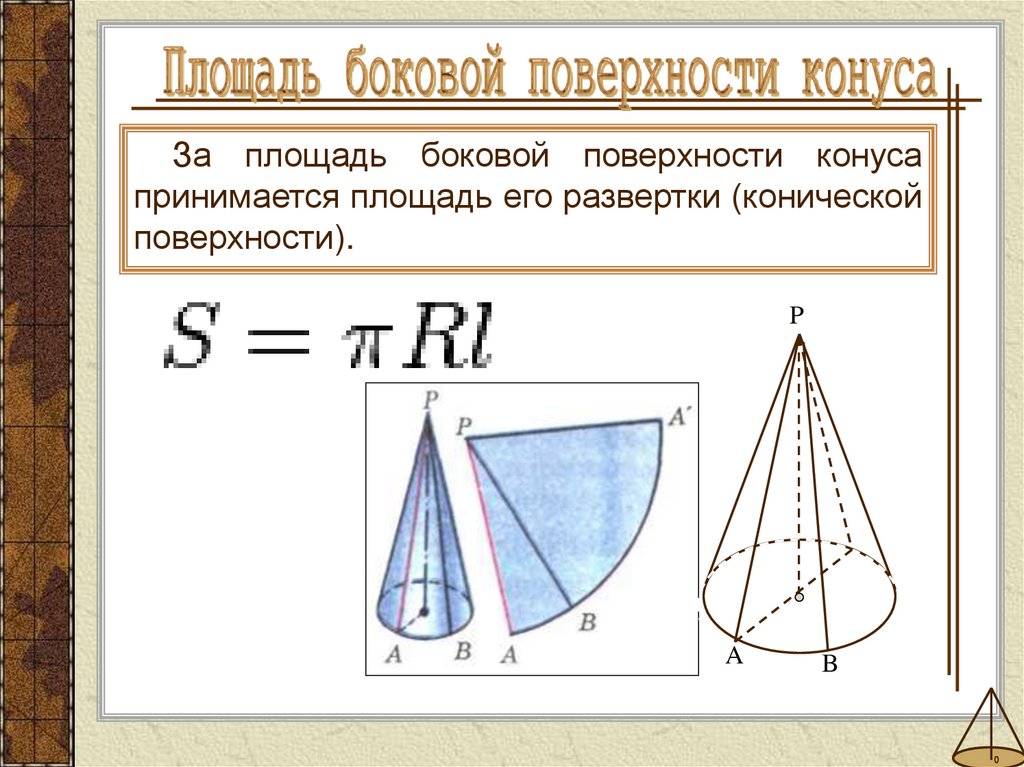
За площадь боковой поверхности конусапринимается площадь его развертки (конической
поверхности).
P
A
B
10.
Площадь боковой поверхности конуса равнапроизведению половины длины окружности
основания на образующую. Площадью полной
поверхности конуса называется сумма площадей
боковой поверхности и основания.
Sкон = π r (l+r)
11.
высотабоковая
поверхность
образующая
основания
радиусы
Усеченным конусом называется пересечение
конуса с полупространством, содержащим
основание конуса и ограниченным плоскостью,
которая параллельна плоскости основания конуса
и пересекает данный конус.
12. Конусные фигуры в быту
13. Конусные тела в архитектуре
14. Конусные тела в архитектуре
15. Конусные тела в архитектуре
16. Конусные тела в архитектуре
17. Конусные тела в архитектуре
18. Конусные тела в архитектуре
19. Конусные тела в архитектуре
20. Конус (моллюск)
Конусы раковиныНаучная классификация
Царство: Животные
Тип:
Класс:
Моллюски
Брюхоногие
Подкласс:
Настоящие улитки
Надотряд:
Caenogastropoda
Отряд:
Инфраотряд:
Надсемейство:
Семейство:
Sorbeoconcha
Neogastropoda
Conoidea
Conidae
Конусы (лат. Conidae) — семейство хищных
брюхоногих моллюсков. Своих жертв, в роли
которых обычно выступают
многощетинковые черви и моллюски
(реже — ракообразные и рыбы), конусы
парализуют с помощью яда. Описано около
500 видов. Большинство представителей
приурочено к тёплым тропическим морям,
однако некоторые способны обитать в
высоких широтах.
Укус некоторых представителей рода Conus
смертельно опасен для человека. В то же
время, яд других видов используют в
фармакологии для изготовления
сильнодействующих обезболивающих
препаратов, не вызывающих наркотической
зависимости.
21. Ползущий по песку Conus textile
22. Conus geographus — самая опасная улитка в мире во время охоты
Conus geographus — самая опасная улитка вмире во время охоты
23.
Яд конуса (Conus magus) применяется какобезболивающее (анальгетик). Например
препарат Ziconotid является синтетической
формой неопиоидного анальгетика —
одного из пептидов конуса, действие
которого превосходит все известные
медициной препараты. Этим ядом
предполагается заменить вызывающие
наркоманию морфины.
Conus
amadis
Конусы очень высоко ценятся
коллекционерами. Конус Глориамарис
(Conus gloriamaris), называемый «Славой
морей», считается самой красивой
раковиной в мире. Описаная ещё в
1777 г. до 1950 г. было известно всего
около двух десятков этих раковин и
поэтому они могли стоить до нескольки
тысяч долларов.
24.
Геометрическаякрасота
Каменска Уральского
25. Наглядное изображение конуса
Видеть в блеске куполов, отраженьеоблаков.
Слушать колокола звон можем мы со всех
сторон.
Колокольною столицей – назван Каменск с
давних пор.
26. Наглядное изображение усечённого конуса
27. Формулы площадей
КонусSкон. = πR(R + L)
Sбок. = πRL
Усеченный конус
Sус.кон. = π(R + r) L + π (R2 + r2)
Sбок. = π(R + r)L
28. Задача 1
Дано: конус, R=12см,L =10см
Найти: 1). Sбок
2). Sкон
Решение:
Sбок. = πRL= π∙12∙10=
120 π
Sкон. = πR(R+L)= π∙12∙(12+10)=
264 π
Ответ: Sбок. = 120 π
Sбок. = 264 π
29.
Самостоятельная работа по теме «Конус»I вариант
II вариант
1. Дано: конус
R=7см, l=3см
R=5см, l=2см.
Найти: Sбок ,Sкон
2. Дано: конус
R=7см, Sбок =21π см2
R=4см, Sбок =12π см2
Найти: l,Sкон
3. Дано: усечённый конус
r1=2см, r2=3см, l=5см
r1=3см, r2=5см, l=12см
Найти: Sбок ,Sус.кон

























 Математика
Математика








