Водородоподобный атом. Орбитальный и собственный моменты импульса электрона и описание различных состояний электрона в атоме

1. Кислицын А.А. Физика атома, атомного ядра и элементарных частиц

14 (0). Водородоподобный атом.
Орбитальный и собственный моменты
импульса электрона и описание
различных состояний электрона в атоме.

2.

Уравнение Шредингера для водородоподобного атома имеет вид:
2m
Ze2
(14.1)
2 E
0
4 0 r
где оператор Лапласа:
2 2
1
1
2
2
2
sin
2 2
r
r r r sin
r sin 2
(14.2)
Решение этого уравнения впервые получил Шредингер в 1926 году. Решение можно найти теми же методами, которыми были решены предыдущие задачи, но в данном случае процедура решения оказывается довольно сложной. Рассмотрим сначала
результаты решения. Вывод формул представлен в
следующей презентации.

3.

Энергия электрона определяется формулой, в точности совпадающей с результатом, полученным в
рамках теории Бора:
2
1 Z me e
En = - 2
2 2
n 8h ε0
4
(14.3)
где n = 1, 2, 3, ... - "главное квантовое число". Часто
применяются следующие условные обозначения
и термины: K-слой, L-слой и т.д.:
n
1
2
3
4
5
6
...
Условное
обозначение
K
L
M
N
O
P
...

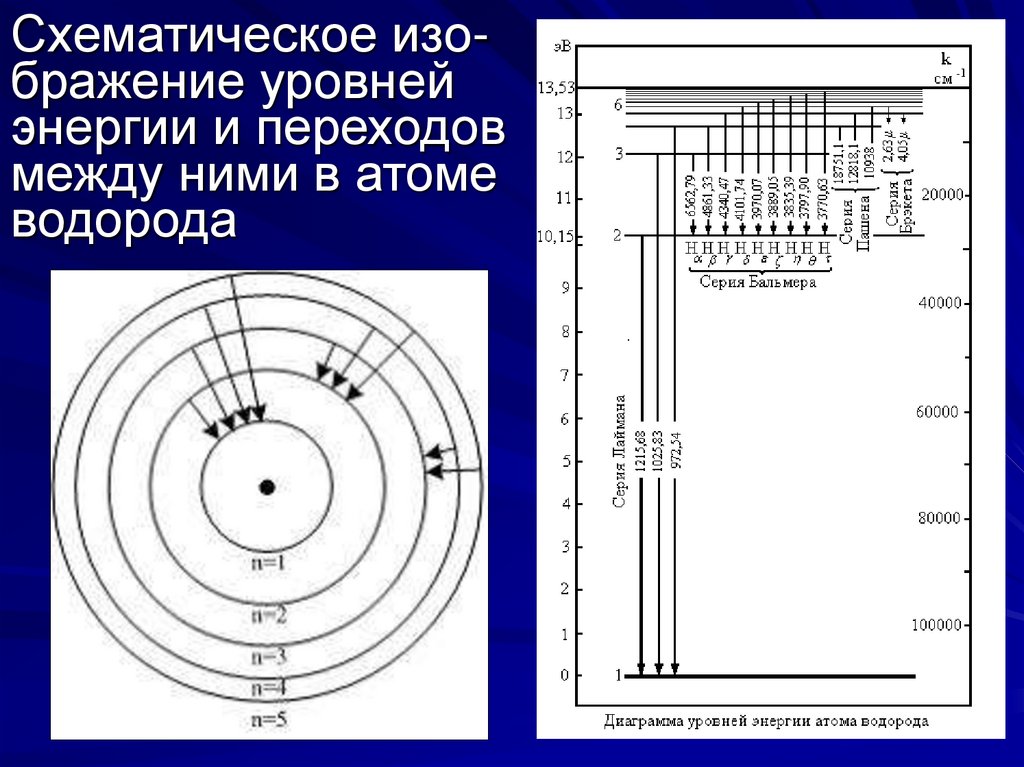
4. Схематическое изо- бражение уровней энергии и переходов между ними в атоме водорода

Схематическое изображение уровней
энергии и переходов
между ними в атоме
водорода

5.

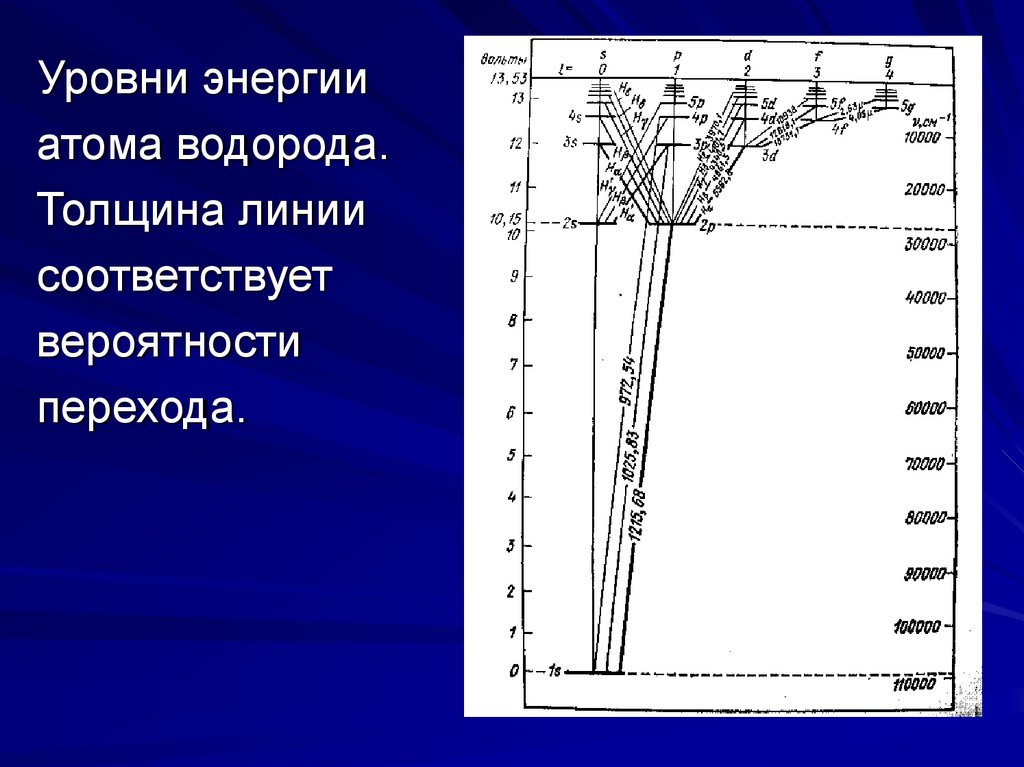
Уровни энергии
атома водорода.
Толщина линии
соответствует
вероятности
перехода.

6.

Момент импульса электрона в атоме определяется орбитальным квантовым числом l:
L=
l (l +1)
(14.4)
где орбитальное квантовое число l может принимать значения l = 0, 1, 2, ..., (n-1). Часто применяются следующие условные обозначения и термины: s-оболочка, p-оболочка и т.д.:
l
0
1
2
3
4
5
...
Условное
обозначение
s
p
d
f
g
h
...

7.

Проекция момента импульса на выделенное направление (например, на направление внешнего магнитного поля) определяется магнитным
квантовым числом m:
(14.5)
LZ = m
Магнитное квантовое число может принимать значения:
m = 0, ±1, ±2, …, ± l,
или:
m = -l, -l+1, -l+2,..., 0, 1, 2, ..., l
всего (2l + 1) значений.

8.

Для наглядности пространственное квантование вектора момента импульса часто изображают графически на векторных диаграммах:
l=1
l=2

9. Графические изображения электронных s-, p- и d-оболочек

Графические
изображения
электронных
s-, p- и dоболочек

10. Графическое изображение 4f-оболочки

11. Схематические изображения электронных оболочек

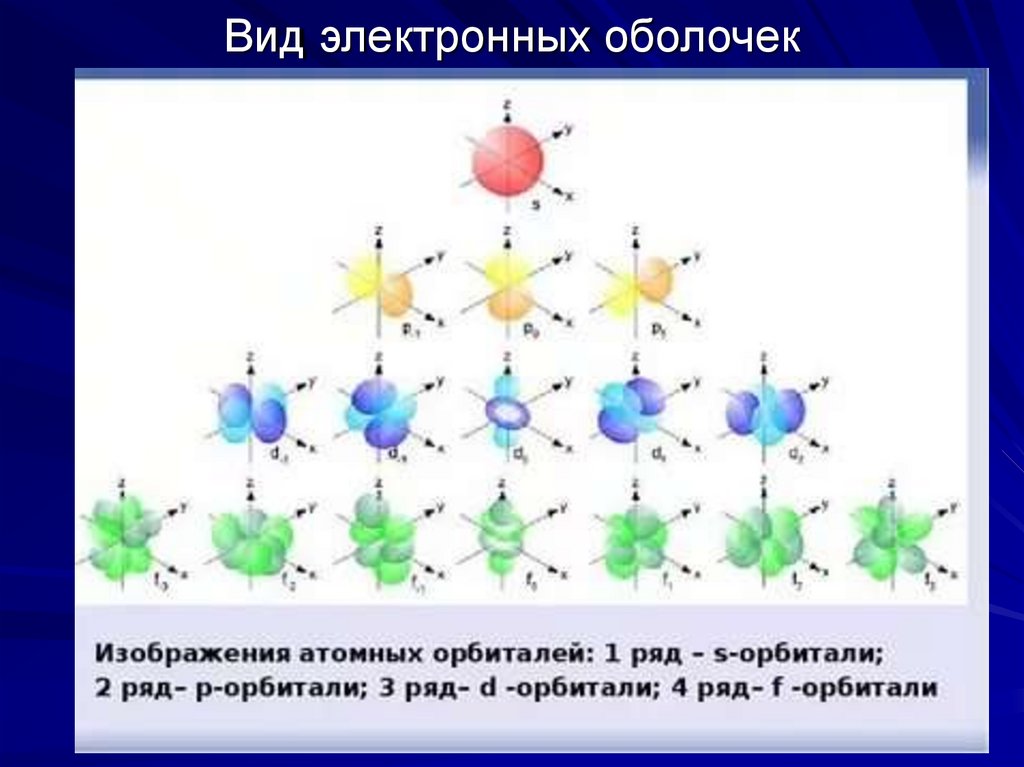
12. Вид электронных оболочек

13.

Спин (собственный механический момент импульса электрона) определяется спиновым квантовым числом s, которое для одного электрона
имеет фиксированное значение s = 1/2:
S=
3
s(s +1)
2
(14.6)
Проекция спина на выделенное направление (например, на направление внешнего магнитного
поля) определяется магнитным спиновым квантовым числом ms:
(14.7)
S = m
Z
s
Магнитное спиновое квантовое число ms может
принимать два значения:
ms = ±1/2
(14.8)

14.

Итак, состояние электрона в атоме определяется
четырьмя квантовыми числами, перечисленными выше:
главным n:
n = 1, 2, 3, ...
орбитальным l:
l = 0, 1, 2, ..., (n-1)
магнитным m:
m = 0, ±1, ±2, …, ± l,
магнитным спиновым ms :
ms = ±1/2

15.

Согласно принципу Паули, для каждого
электрона в атоме эта четверка чисел
должна быть уникальной, или по-другому: в
атоме не может быть двух электронов с
одинаковой четверкой квантовых чисел, т.е.
хотя бы одним квантовым числом каждый
электрон должен отличаться от всех
остальных электронов в атоме. Подробнее
принцип Паули рассмотрим в одной из
следующих презентаций.

16.

Число различных состояний, соответствующих
данному орбитальному квантовому числу l, равно 2(2l+1) (это максимально возможное число
электронов на оболочке), а число состояний,
соответствующих данному главному квантовому
числу n, равно:
n-1
(14.9)
2(2l +1) = 2n
2
l=0
это максимально возможное число электронов на
слое.