Классификация данных гравитационным методом с помощью дообучения нейронных сетей

1.

Инженерная школа ядерных технологий
Направление подготовки 01.04.02 «Прикладная математика и информатика»
Отделение экспериментальной физики
КЛАССИФИКАЦИЯ
ДАННЫХ
ГРАВИТАЦИОННЫМ
МЕТОДОМ С ПОМОЩЬЮ
ДООБУЧЕНИЯ
НЕЙРОННЫХ СЕТЕЙ
Выполнил
студент гр. 0ВМ02
Научный
руководитель
доцент ОЭФ, к.ф.-м.н.
Томск 2022
Захаров В.К.
Крицкий О.Л.

2. Цели и задачи

Цель Магистерской диссертации: классификация данных гравитационным методом с помощью
дообучения нейронных сетей
Задачи:
• Создать единый класс, позволяющий правильно задавать параметры при начальном предобучении сети на
заданных данных;
• Построить, использовать и получить ожидаемые метрики от двух сверточных нейронных сетей (ResNet18,
ResNet101) с классическим методом обучения градиентного спуска.
• Построить на основе данных нейронных сетей новую модель, с использованием гравитационного метода
обучения и получить метрики.
• Сравнить результаты прогнозирования двумя методами, наметить следующий этап изучения данного
метода и его улучшения.
2

3. Актуальность работы

Проблема: существование неразмеченных
наборов данных, которые необходимо
классифицировать.
Невозможность провести адекватную
классификацию с помощью нейронной сети без
использования заранее предобученной модели.
Минимизация, либо полное избавление от разметки данных
перед первоначальным обучением нейронной сети.
Необходимость метода обучения нейронной сети, основанного на
степени уверенности в принадлежности данных к одному из
классов, начиная с начального момента классификации.
Решение: создание уникального метода обучения сетей, позволяющего работать с неразмеченными
данными и объединяющего возможность использования для любых сетей и входных данных.
3

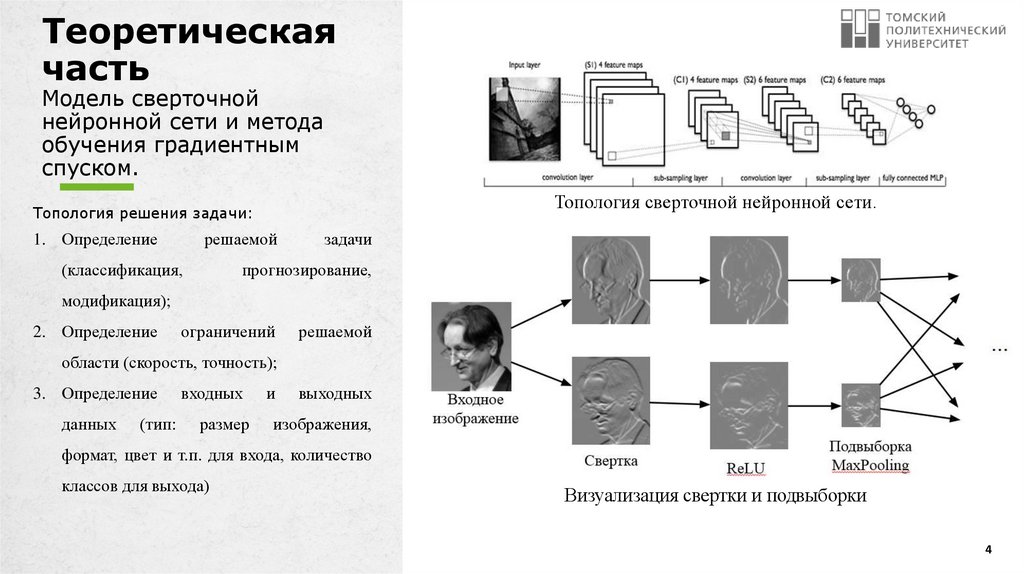
4. Теоретическая часть Модель сверточной нейронной сети и метода обучения градиентным спуском.

Топология сверточной нейронной сети.
Топология решения задачи:
1. Определение
решаемой
(классификация,
задачи
прогнозирование,
модификация);
2. Определение
ограничений
решаемой
области (скорость, точность);
3. Определение
данных
(тип:
входных
размер
и
выходных
изображения,
формат, цвет и т.п. для входа, количество
классов для выхода)
Визуализация свертки и подвыборки
4

5. Теоретическая часть. Гравитационное обучение.

Описание графического представления
гравитационного обучения:
1. Представим область всех данных в
виде набора вероятностей
(уверенности в том, что экземпляр
принадлежит к одному из классов).
2. Среди получившихся вероятностей
выберем данные, которые имеют
наибольшую степень уверенности по
каждому из классов.
3. Обучение нейронной сети на
первоначальных точках и
последующих за ними данных, при
преодолении порога степени
уверенности принадлежания к классу
по каждому из экземпляров.
5

6. Теоретическая часть. Гравитационное обучение.

Представим, для разбиения M значений на
N признаков, матрицу в виде (1).
Тогда на каждом последующем шаге
обучения нейросеть будет давать
модифицированную матрицу по всем данным
значениям, как вероятности их
принадлежности к определенному признаку.
Функция, на основе функции Хевисайда,
позволяет при наложении на каждую строку
матрицы получить выбор данных, которые
уже классифицированны, что позволяет
задать первоначальную точность на каждом
из шаге (λ).
Тогда согласно 3 и 4 получим новые
данные для обучения сети и происходит
возврат на первый пункт.
6

7. Результаты экспериментов

В результате проведенного исследования
были получены следующие результаты:
1. На классическом наборе данных в виде
рукописных цифр (MNIST), нейросеть,
натренированная методом градиентного
спуска справилась значительно лучше
(точность у метода градиентного спуска
на 7.87% и 7.36% больше, чем у
гравитационного
метода
для
сетей
ResNet18 и ResNet101 соответственно).
2. На
наборе
данных
из
одежды
(FashionMNIST)
нейронная
сеть,
натренированная
методом
гравитационного обучения справилась
незначительно хуже (на 0.83% и 1.96%
меньше правильно определенных образов
для
сетей
ResNet18
и
ResNet101
соответственно).
Результаты метрик полученные обеими моделями с
тренировкой методом градиентного спуска.
Метрика
ResNet18
MNIST
ResNet101
MNIST
ResNet18
FashionMNIST
ResNet101
FashionMNIST
Вероятность
ошибки
0,0498
0,0261
0,0782
0,0501
Вероятность
верных
0,9502
0,9739
0,9218
0,9499
TP
55618
56078
53323
53349
FP
2127
705
3433
1352
FN
861
892
1259
1654
TN
1394
2325
1985
3645
Результаты метрик полученные обеими моделями с тренировкой
гравитационным методом.
Метрика
ResNet18
MNIST
ResNet101
MNIST
ResNet18
FashionMNIST
ResNet101
FashionMNIST
Вероятность
ошибки
0,1285
0,0997
0,0864
0,0697
Вероятность
верных
0,8715
0,9003
0,9135
0,9303
TP
20347
50866
48358
53663
FP
971
5335
4108
3503
FN
1943
647
1079
679
TN
8682
3152
6455
2155
7

8. Заключение

Разработан метод гравитационного обучения нейронных сетей, выбраны оптимальные
параметры для тренировки сетей. Также было проведено сравнение модели с другими
нейросетями, построенными на основе обучения методом градиентного спуска и сравнены
метрики на двух различных датасетах.
Полученные метрики позволяют судить о работспособности метода, однако, из-за его
недостаточной изученности, пока что невозможно подобрать наиболее идеальные параметры для
классификации данных. Данная работа направлена на продолжение исследований данного
метода обучения сетей, что даст возможность для более обширного понимания применимости
данного метода при классификации данных.
Метод гравитационного обучения был реализован на языке Python. При тестировании
использовался также яхык программирования Python и было произведено в среде Visual Studio
Code с использованием библиотек Pandas, TorchVision, PyTorch, numpy.
Метод обучения получил высокую оценку при классификации данных, а иакже
разработана программа дальнейшего исследования.
8

9. Targets and goals

The purpose: classification of data by the gravitational method with the help of additional training of
neural networks
Tasks:
1. Create a single class that allows you to correctly set the parameters during the initial pre-training of
the network on the given data;
2. Build, use and get expected metrics from two convolutional neural networks (ResNet18, ResNet101)
with classical gradient descent learning method.
3. Build a new model based on neural network data using the gravitational learning method and get
metrics.
4. Compare the results of forecasting by two methods, outline the next stage in the study of this
method and its improvement.
9

10. Conclusion

Was developed a method for gravitational training of neural networks, the optimal parameters
for training networks were selected. The model was also compared with other neural networks built on
the basis of gradient descent learning and the metrics were compared on two different datasets.
The obtained metrics make it possible to judge the performance of the method, however, due
to its insufficient knowledge, it is not yet possible to select the most ideal parameters for data
classification. This work is aimed at continuing research on this method of learning networks, which will
provide an opportunity for a broader understanding of the applicability of this method in data
classification.
The gravity learning method was implemented in Python. The testing also used the Python
programming language and was carried out in the Visual Studio Code environment using the Pandas,
TorchVision, PyTorch, Numpy libraries.
The training method was highly appreciated in the classification of data, and a program for
further research was also developed.
10

11. СПАСИБО ЗА ВНИМАНИЕ!

Выполнил студент гр. 0ВМ02 В.К. Захаров
E-mail: [email protected]
Tel: +7 913 871 35-64
Томск 2022
11