Складне висловлювання

1.

ЛЕКЦІЯ
на тему:
“СКЛАДНЕ ВИСЛОВЛЮВАННЯ”
П Л А Н.
1. Поняття складного висловлювання та його
види.
2. Відношення між складними
висловлюваннями.

2.

ЛІТЕРАТУРА
1. Гетманова А.Д. Логика. – М.,1995. – с.68-83
2. Кириллов В.И., Старченко А.А. Логика. – М.,
1995. – с.158-163
3. Конверський А.Є. Логіка (традиційна та
сучасна). – К.,2004. – с.308-321
4. Мозгова Н.Г., Мозговий A.M. Логіка. – К.,2005.
– с.121-130
5. Тофтул М.Г. Логіка. – К., 2003. – с.90-116

3.

1. Поняття складного висловлювання та його
види.
Складне висловлювання (молекула) включає в себе
два і більше простих (елементарних або атомів).
Атоми позначають A, B, C, D … ці символи
називають пропозиційними змінними.
Молекула в свою чергу складається з двох і більше
атомів.
Розділ сучасної логіки, який вивчає складне
висловлювання називають логікою висловлювань.

4.

Логічні сполучники та логічні операції.
Основними питаннями дослідження логіки
висловлювань є:
1. Як з атомарних висловлювань утворюються
молекулярні;
2. Як залежить значення істинності молекули від
значень істинності атомів, які її складають.
Складні
висловлювання
утворюються
з
елементарних
за
допомогою
логічних
сполучників (пропозиційних зв’язок), яким
відповідають логічні операції, що позначаються
відповідними символами логічних операцій або
логічними операторами. Цей зв’язок можна
зобразити в таблиці:

5.

Логічний
сполучник
Логічна операція
Символ
логічної
операції
І
Кон’юнкція(від
латинського conjunctio –
зв’язок, об’єднання)
Або
Диз’юнкція(від
латинського disjunctio –
роз’єднання, розрізнення)
Або … , або …
Сильна (строга)
диз’юнкція
Якщо … , то
…
Імплікація(від латинського
implico - тісно зв’язую)
Якщо і тільки
якщо … , то …
Подвійна імплікація
(еквіваленція)
Невірно, що А
або просто: “Не
А”
Заперечення
~А

6.

Утворення нових висловлювань із вихідних
за допомогою логічних сполучників називають
логічними операціями. Кожна логічна операція
визначається так, що значення істинності
молекулярного висловлювання залежить лише
від значень істинності складаючих його атомів,
а не від їх змісту чи смислової характеристики
отриманого висловлювання.
Якщо в молекулу входять n cкладаючих її
атомів, то для них можливі 2n різних комбінацій
значень істинності атомів і таблиця істинності
молекули буде складатись із 2n рядків.

7.

Враховуючи ці вимоги дамо визначення логічним
операціям.
*Кон’юнкція. Кон’юнкцією висловлювань А та В
називають висловлювання А В (читається “А і В”) ,
яке є істинним тоді і тільки тоді, коли істинними
є всі атоми. Цьому визначенню відповідає таблиця:
А
В
1)
1
1
1
2)
1
0
0
3)
0
0
1
4)
0
0
0

8.

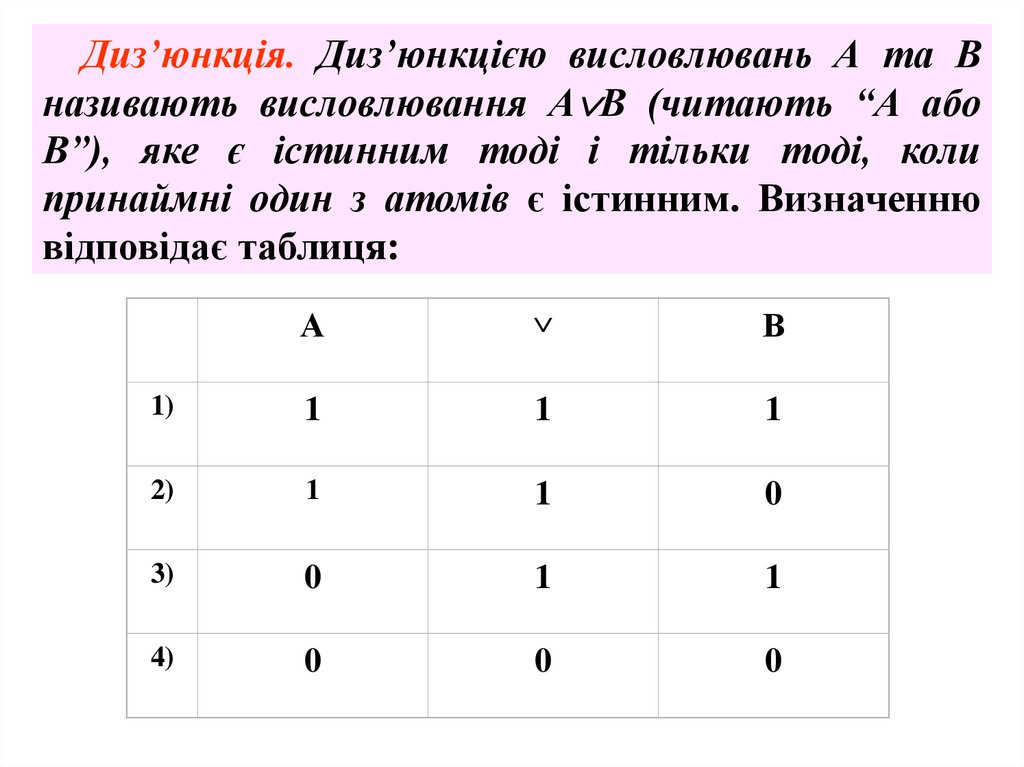
Диз’юнкція. Диз’юнкцією висловлювань А та В
називають висловлювання А В (читають “А або
В”), яке є істинним тоді і тільки тоді, коли
принаймні один з атомів є істинним. Визначенню
відповідає таблиця:
А
В
1)
1
1
1
2)
1
1
0
3)
0
1
1
4)
0
0
0

9.

В наведеному прикладі сполучник “або”
використовується
в
з’єднувальнороз’єднувальному смислі, тобто “А або В, або
обоє”. Цьому смислу відповідають також: “А
і/або В”, “і А, і В чи А або В”, “А, якщо не В”
тощо.
В українській мові ( як і в багатьох інших)
сполучник “або” може використовуватись і в
суто роз’єднувальному сенсі, тобто “або … , або
…”. Цей смисл відповідає логічній операції
сильної (строгої) диз’юнкції.

10.

* Сильна диз’юнкція. Сильною диз’юнкцією
висловлювань А та В називають висловлювання
А В (читають “або А, або В”), яке є істинним
тоді і тільки тоді, коли тільки один з атомів є
істинним. Цьому визначенню відповідає таблиця:
А
В
1)
1
0
1
2)
1
1
0
3)
0
1
1
4)
0
0
0

11.

*Імплікація. Імплікацією висловлювань А та В
називають висловлювання А В (читають “якщо
А, то В”), яке є хибним тоді і тільки тоді, коли А
істинне, а В хибне. Визначенню відповідає таблиця:
А
В
1)
1
1
1
2)
1
0
0
3)
0
1
1
4)
0
1
0

12.

*Подвійна імплікація. Подвійною імплікацією
(еквіваленцією) висловлювань А та В називають
висловлювання А ↔ В (читають “якщо і тільки якщо
А, то В”), яке є істинним тоді і тільки тоді, коли
значення
істинності
атомів
співпадають.
Визначенню відповідає таблиця:
А
В
1)
1
1
1
2)
1
0
0
3)
0
0
1
4)
0
1
0

13.

Заперечення. Запереченням висловлювання А
називають висловлювання ~А (читають “невірно,
що А” або просто “не А”), яке є істинним, коли А –
хибне, і навпаки. Цьому визначенню відповідає
таблиця:
А
~А
1
0
0
1

14.

2. Відношення між складними
висловлюваннями.
Відношення еквівалентності
Серед формул логіки висловлювань є такі, які
незалежно від значень істинності їх атомів є завжди
істинними. Їх називають тотожно істинними
формулами або тавтологіями.
*Дві формули F1 та F2 є еквівалентними
(рівносильними) тоді і тільки тоді, коли їх подвійна
імплікація (F1 F2) – тавтологія.
Перевірку еквівалентності двох формул
здійснюють за допомогою таблиць істинності.
Якщо значення їх істинності в цілому однакові, то
відповідні формули еквівалентні.

15.

Деякими елементарними еквівалентностями логіки
висловлювань є такі::
1) А В ~ А В – вираження імплікації через
диз’юнкцію та заперечення.
2) а) ~ (А В) ~ А ~ В;
в)~ (А В) ~ А В - закони де Моргана.
3) А В (А В) (В А) – подвійна імплікація
через імплікацію та кон’юнкцію.
4) Скориставшись еквівалентністю (1) дістанемо:
А В ( А В) ( В А).
5) Скориставшись де Моргана (2b) дістанемо:
А В (А В) (В А).

16.

Особливості імплікації
Якщо всі логічні операції є симетричними, то
імплікація не є симетричною операцією.
Саме тому, ми давали її визначення не через
випадок істинності, а через випадок хибності.
З таблиці істинності імплікації видно, що:
1. Імплікація є завжди істинною, при хибному
антецеденті, незалежно від значення істинності
консеквента (рядки таблиці 3, 4). В обох
випадках А є хибним, але в третьому рядку В є
істинним, а в 4-му В – хибне. Отже, ми можемо
визначити істинність імплікації знаючи тільки
значення істинності лівої частини. Якщо вона
хибна, то імплікація є істиною.

17.

2. Імплікація є завжди істинною, при істинному
консеквенті (1, 3 рядки), незалежно від значення
істинності антецедента. Так, в першому рядку він
істинний, а в третьому – хибний. Це теж дозволяє
визначати істинність імплікації тільки по
значенню істинності консеквента.
Відношення логічного слідування
З формули F1 логічно слідує формула F2 тоді і
тільки тоді, коли їх імплікація (F1 F2) є завжди
істинною формулою (тавтологією).*
Між відношенням логічного слідування (├ ) та
імплікацією ( ) існує тісний зв’язок, але їх не слід
плутати.

18.

Імплікація – це висловлювання, що складається
з двох елементарних висловлювань і серед наборів
її значень істинності може бути “хиба”. *Логічне
слідування
–
це
відношення
між
двома
висловлюваннями, яке є завжди істинною
імплікацією.
Для перевірки чи є F2 логічним наслідком F1
необхідно:
1) з’єднати їх знаком імплікації (F1 F2);
2) побудувати таблицю для отриманої формули;
3) якщо ця формула є тавтологією, то з F1 логічно
слідує F2 (F1 ├ F2); якщо ця формула не є
тавтологією, то з F1 логічно не слідує F2 .

19.

ВИСНОВОК
Все
розмаїття
складних
висловлювань
національної живої мови можна, як бачимо,
звести до чотирьох видів логічних операцій
(пропозиційні константи).
Користуючись набором символів мови логіки
висловлювань можна формалізувати не тільки
окремі речення, але й цілі системи висловлювань
з метою їх подальших перетворенювань,
систематизації та спрощення.