Закони магнітостатики. Магнітне поле прямого та колового провідників зі струмом. (Лекція 13)

1. Лекція № 13. Закони магнітостатики

1. Магнітне поле прямого та колового
провідників зі струмом
2. Взаємодія струмів
3. Закон повного струму, магнітне поле
соленоїда. Вихровий характер магнітного
поля.
4. Робота при переміщенні провідника зі
струмом в магнітному полі. Енергія
провідника зі струмом.

2. 1. Магнітне поле прямого та колового провідників зі струмом.

Досліджуючи магнітне поле провідників зі
струмом заданої конфігурації, французькі вчені
Ж. Біо і Ф. Савар експериментально
встановили,
що індукція магнітного поля B складним чином
залежить від розмірів і конфігурації провідника,
завжди пропорційна силі струму I , що протікає у
ньому та зменшується при віддаленні точки
спостереження від провідника (~ 1 ... 12 )
r
ЖанБатист
Біо
Фелікс
Савар
r

3.

Французький астроном, математик і фізик
П. Лаплас
теоретично узагальнив ці експериментальні факти і отримав
математичні формули, розрахунки за якими завжди збігалися
з емпіричними вимірюваннями
індукції магнітного поля B
.
П’єр-Сімон
Лаплас

4.

Закон, що дозволяє визначити величину
індукції магнітного поля B
. , яку створює у деякій
точці простору елемент провідника dl
із постійним
струм I отримав назву закону Біо-Савара-Лапласа:
0 I dl r
dB
3
I
4
r
або у скалярному вигляді
0 Іdl sin
dB
4 r 2
dl
I

5.

0 Іdl sin
dB
2
4 r
r – радіус-вектор, що з’єднує елемент провідника
довжиною dlіз точкою простору, у якій
визначається індукція магнітного поля;
– кут між векторами I dl і r ;
7 Гн
0 – магнітна стала, 0 4 10
;
м
– магнітна проникність середовища, яка показує,
у скільки разів індукція магнітного поля у
середовищі більша, ніж у вакуумі.

6.

Цей закон дозволяє розрахувати індукцію
магнітного поля провідника зі струмом довільної
конфігурації
при
застосуванні
принципу
суперпозиції магнітних
полів – вектор індукції
магнітного поля B
, створений провідником у
вибраній точці простору, дорівнює векторній сумі
індукцій, що створюються окремими елементами
цього струму в даній точці.
B dB
L
інтегрування здійснюється вздовж усієї довжини
провідника.

7.

Для розрахунку індукції магнітного поля провідників зі струмом різних конфігурацій у довільних точках простору використовують формулу, що об’єднує закон
Біо-Савара-Лапласа та принцип
суперпозиції магнітних полів:
I dl r
0 I dl r або
H
B
3
3
4 r
r
L
L 4
де H– напруженість магнітного поля – характеристика, що не залежить від магнітних властивостей середовища, в якому знаходиться
провідник:
B
H
0
Одиницею вимірювання напруженості магнітного поля є 1 А/м.

8.

Розглянемо приклади застосування закону БіоСавара-Лапласа
для
розрахунку
індукції
магнітного поля провідників конфігурацій, що
зустрічаються найчастіше.
1. Індукція магнітного поля у центрі колового
провідника радіуса R, по якому проходить струм
силою I.
dl
I
Запишемо закон
Біо-Савара-Лапласа у
загальному вигляді:
R
dB
0 I dl r
B
3
r
L 4

9.

враховуючи, що усі ділянки провідника у центрі колового витка
створюватимуть
елементарні
значення індукції магнітного поля
одного напрямку, перепишемо
закон
Біо-Савара-Лапласа
у
скалярному вигляді:
0 Іdl sin
B
4 r 2
L
dl
I
R
dB
де dl – довільно обраний елемент провідника зі струмом силою І,
r – відстань від елементу провідника dl до точки
визначення індукції магнітного поля, дорівнює
радіусу кола r R ,
L – довжина колового витка;
– кут між елементом провідника dl і радіусом кола;
тому / 2, а sin 1.

10.

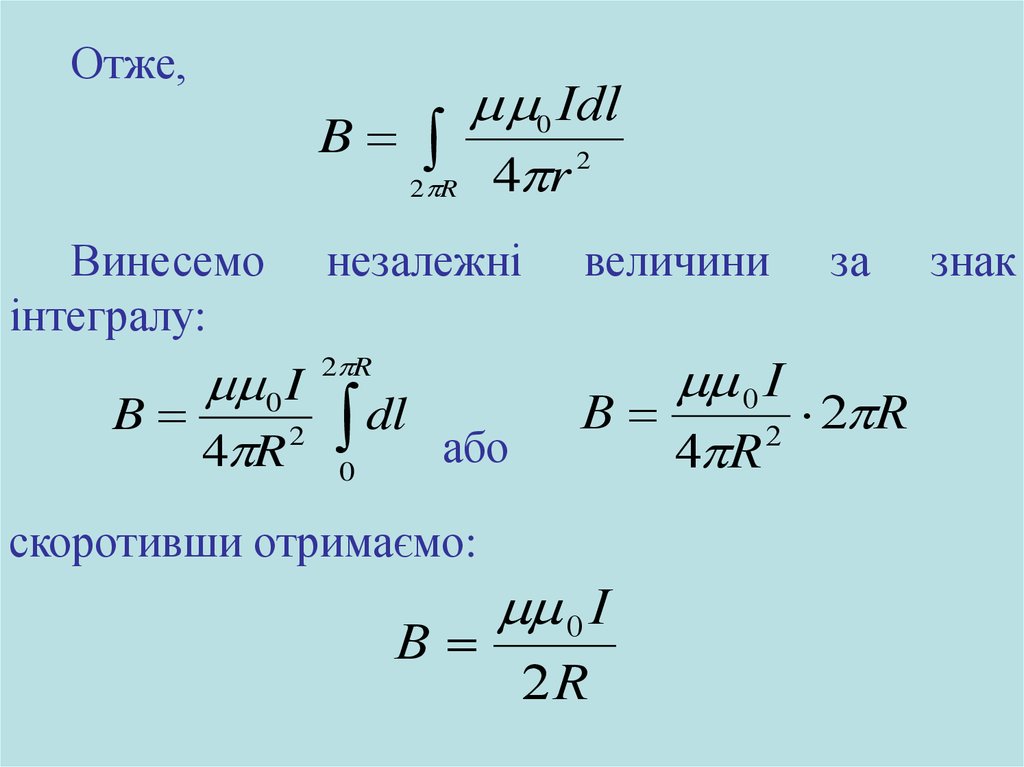
Отже,
Винесемо
інтегралу:
0 I
B
4 R 2
0 Іdl
B
2
2 R 4 r
незалежні
величини
2 R
0 I
B
2 R
2
4 R
dl
0
або
скоротивши отримаємо:
B
0 I
2R
за
знак

11.

2. Індукція магнітного поля на відстані а від
прямолінійного провідника, по якому тече
струм силою І.
Запишемо закон
Біо-Савара-Лапласа у
dl
r
загальному вигляді:
I
r
d
0 I dl r
B
3
a
4
r
L
O
0
dB

12.

Щоб визначити індукцію
магнітного поля провідника зі
струмом у точці О, розіб’ємо
провідник на нескінченно
малі
ділянки довжиною dl . Вектори dl
індукції магнітного поля у точці
О,
що
створює
кожна I
елементарна ділянка провідника
направлені в один бік вздовж
одної прямої перпендикулярно
до площини рисунка до нас.
Тому
результуюча
індукція
магнітного поля всіх елементів
струму Idl у точці О:
0 Іdl sin
B
2
4
r
2
1
r0
r
a
d
O
dB

13.

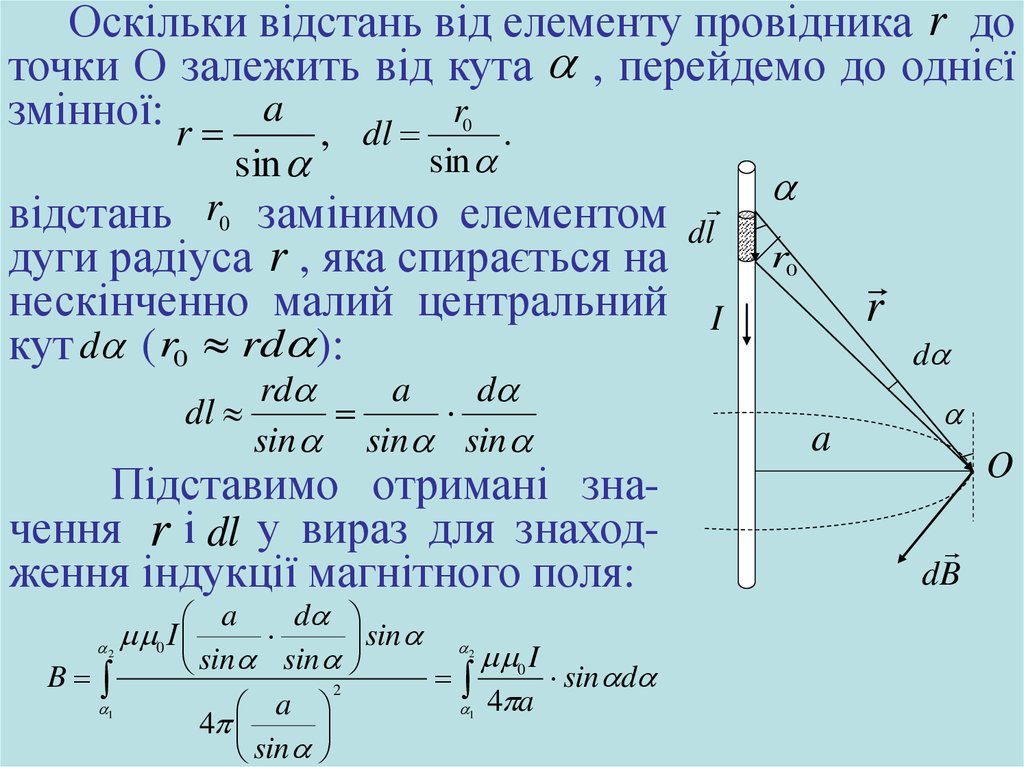
Оскільки відстань від елементу провідника r до
точки О залежить від кута , перейдемо до однієї
змінної: r a , dl r .
sin
0
sin
відстань r0 замінимо елементом dl
дуги радіуса r , яка спирається на
нескінченно малий центральний
кут d ( r0 rd ):
rd
a
d
dl
sin sin sin
Підставимо отримані значення r і dl у вираз для знаходження індукції магнітного поля:
d
a
0 І
sin
0 I
sin sin
B
sin d
2
4 a
a
4
sin
2
2
1
1
r0
r
I
a
d
O
dB

14.

Винесемо сталі величини за знак інтегралу та
здійснимо інтегрування:
0 I
B
sin d
4 a
2
1
Індукція магнітного поля прямолінійного
провідника скінченної довжини:
0 I
cos 1 cos 2
B
4 a
Якщо провідник нескінченно довгий, 1 0 а
. 2 , то індукція магнітного поля нескінченно
довгого прямолінійного провідника:
0 I
B
2 a

15.

2. Взаємодія струмів
Провідники по яким проходять електричні
струми взаємодіють один з одним через власні
магнітні поля. Цю силу взаємодії можна визначити
поєднуючи закон Біо-Савара-Лапласа із законом
Ампера. За законом Біо-Савара-Лапласа елемент
струму I 1dl1 у точці О, що знаходиться на відстані r .
створює магнітне поле індукцією
0 I1 dl1 r
dB
4
r3

16.

На елемент струму I dl , поміщений у точку О,
за законом Ампера, діятиме сила з боку магнітного
поля, що створюється елементом струму I1dl1
2
2
dF12 I 2 dl2 dB
підставивши значення індукції магнітного поля у
точці О в закон Біо-Савара-Лапласа, отримаємо
загальний закон Ампера:
0 I 2 dl2 I1dl1 r
dF12
3
4
r

17.

Застосовуючи закон Ампера для двох
нескінченно довгих прямолінійних паралельних
провідників, можна отримати силу взаємодії, що
припадає на одиницю їх довжини:
dF 0 2 I1 I 2
dl
4
r
де r – відстань між провідниками.
Використовуючи правило свердлика та правило
лівої руки, можна визначити, що провідники з
однаковим напрямом струмів взаємно притягуються, а з різним – відштовхуються.

18.

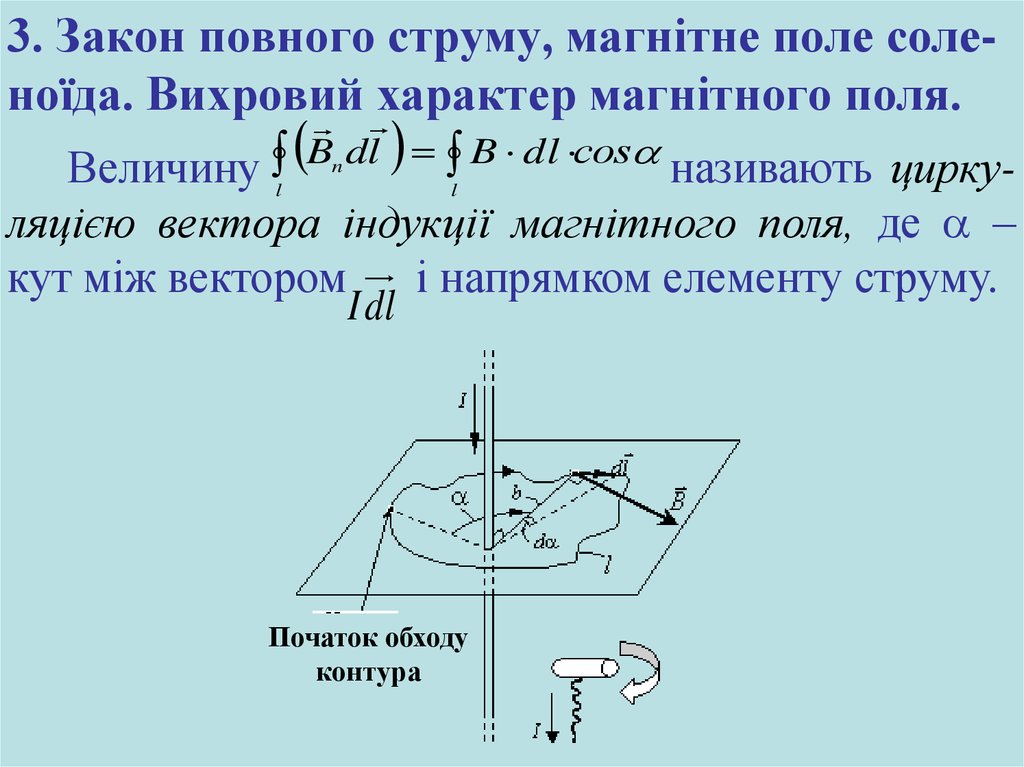
3. Закон повного струму, магнітне поле соленоїда. Вихровий
характер
магнітного
поля.
B dl B dl сos
Величину
називають циркуn
l
l
ляцією вектора індукції магнітного поля, де –
кут між вектором і напрямком елементу струму.
I dl
Початок обходу
контура

19.

Знайдемо циркуляцію вектора індукції магнітного поля прямого провідника зі струмом. Індукція
магнітного поля прямого нескінченого провідника
із струмом дорівнює:
0 I
B
2 R
де R – відстань від провідника до точки, в якій
визначається В.
Охопимо провідник колом радіуса R. Тоді
0 i
Bn dl 2 R dl
l
Так як І, , 0 і R величини сталі, маємо:
0 I 2 R
0 I 2 R
B
dl
dl
або Bn dl
n
2 R 0
l
2 R
l
і
Bn dl 0 I
l

20.

Сформулюємо закон повного струму або
теорему про циркуляцію вектора індукції
магнітного поля в загальному вигляді, циркуляція
вектора індукції магнітного поля постійних
струмів по довільному замкненому контуру
дорівнює алгебраїчній сумі сил струмів, які
охоплюються цим контуром, помноженій на
магнітну сталу і магнітну проникність середовища:
n
B dl І
n
l
n
0
і 1
і
де І – сума струмів, які
охоплюються контуром.
і 1
і

21.

Отже, робота при перенесенні пробного
одиничного елемента струму в магнітному полі в
загальному випадку не дорівнює нулеві, тому його
називають непотенціальним або вихровим.
Характерною ознакою вихрового поля є
замкненість його силових ліній.

22.

При застосуванні закону повного струму
необхідно враховувати правило знаків: якщо
напрямок обходу контуру співпадає з напрямом
обертального руху свердлика (правого гвинта), то
охоплені контуром струми, напрями яких
співпадають із напрямом поступального руху
свердлика, записують із знаком «+», а ті, що не
співпадають – із знаком «–».

23.

Закон повного струму і закон Біo-СавараЛапласа використовують для обчислення індукції
магнітного поля, що створює система провідників
зі струмом.
Закон Біо-Савара-Лапласа застосовують у тому
випадку, коли легко провести інтегрування вздовж
провідника довжиною l, в інших випадках
застосовують закон повного струму, довільно
обираючи контур симетричної форми з метою
спрощення інтегрування.
l

24.

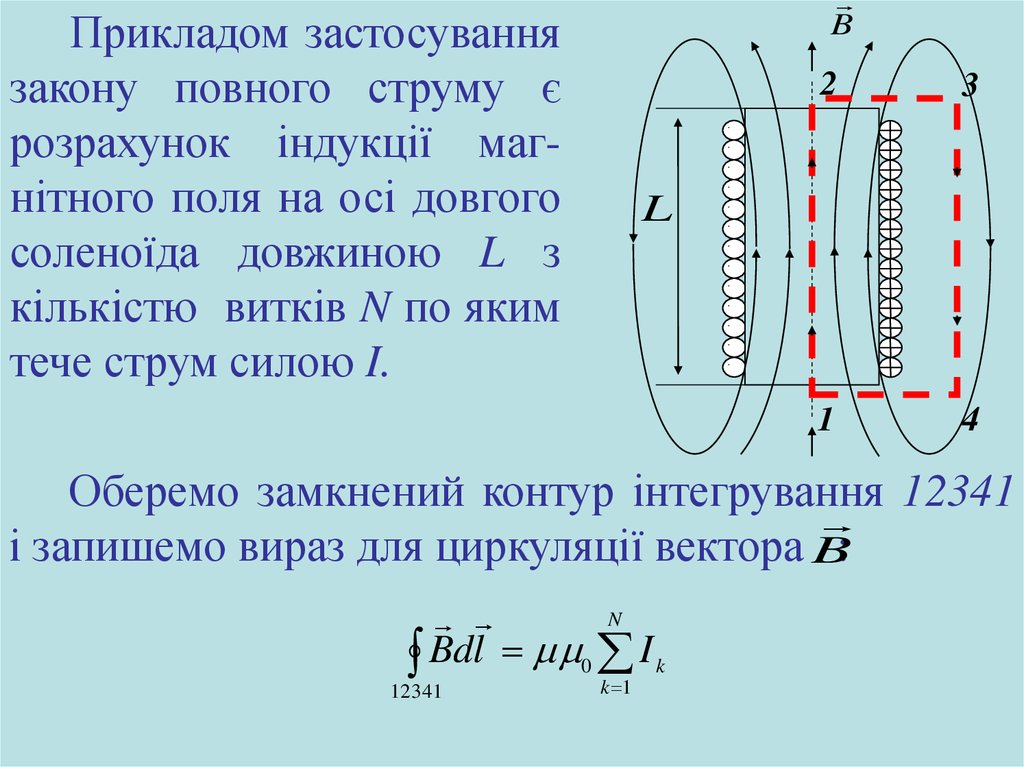
B
Прикладом застосування
закону повного струму є
розрахунок індукції магнітного поля на осі довгого
соленоїда довжиною L з
кількістю витків N по яким
тече струм силою I.
2
3
1
4
·
·
·
·
L
·
·
·
·
·
·
·
·
·
Оберемо замкнений контур інтегрування 12341
і запишемо вираз для циркуляції вектора B:
N
Bdl 0 I k
12341
k 1

25.

Циркуляцію вектора по замкненому контуру
можна подати у вигляді чотирьох доданків
Bdl Bdlcos B
,dl Bdlcos B
,dl
Bdl cos B ,dl Bdlcos B
,dl
12341
12
41
0
90
90
23
34 0
1
0
0
Bdl Bdlcos B
,dl B dl BL
12341
12
12
0
1
Оскільки обраний контур охоплює N витків по
кожному з яких тече струм
силою I, то
N
I
k 1
k
NI
Підставляючи у закон повного
струму отримані
вирази циркуляції вектора Bі суми сил струмів
матимемо:
BL 0 NI

26.

тоді індукція магнітного поля на осі довгого
соленоїда становитиме
NI
B 0
0 nI
L
де n – кількість витків соленоїда на одиницю
довжини.

27.

Явище виникнення магнітного поля навколо
провідників зі струмом
використовують для
виготовлення електромагнітів – пристроїв,
здатних створювати власні магнітні поля при проходженні електричного струму у витках обмотки.

28.

Звичайно
електромагніт
складається з обмотки і
феромагнітного осердя, який
набуває властивостей магніту
при проходженні по обмотці
струму (на рисунку наведено
найпростіший електромагніт –
електропровід
в
ізоляції
намотаний навколо феромагнітного осердя).
Електромагніти використовуються там, де необхідне магнітне поле, яке можна швидко і
легко змінити, наприклад у
побутових приладах (телевізор,
магнітофон, електробритва),

29.

у пристроях техніки зв’язку
(телефон, телеграф, радіо), в
електричних машинах (електрогенератори та електродвигуни),
у
пристроях
промислової
автоматики
(пускачі, перемикачі, реле та
інше), в електромагнітних
сепараторах для очищення
механічних сумішей від
магнітних предметів.

30.

Широкого застосування електромагніти набули
в електромагнітних механізмах, що здійснюють
поступально-поворотні рухи чи гальмувальні
процеси – вантажопідйомні електромагніти (див.
рис.), металорізальні верстати, магнітні замки,
релейні
та
пускові
пристрої,
механізми
автоматичного вимикання, гальмові пристрої тощо.

31.

4. Робота при переміщенні провідника зі
струмом в магнітному полі. Енергія
провідника зі струмом.
При переміщенні провідника зі струмом в
магнітному полі виконується робота
dA IdФ
Енергія магнітного поля замкненого провідного контуру зі струмом І та індуктивністю L
LI
Wм
2
2

32.

Енергію
формулою
магнітного
поля
визначають
за
1 1 2
Wм
BV
2 0
Якщо врахувати формулу
зв’язку вектора
індукції магнітного поля B і вектора напруженості
магнітного поля H
B 0 H
то енергія магнітного
дорівнюватиме
поля
1
Wм BHV
2
у
даній
точці

33.

А об’ємна густина енергії магнітного поля в
околі кожної точки
Wм
простору м V
визначатиметься
значеннями векторних характеристик поля:
1
м BH
2

34. Лекція № 13. Закон Біо-Савара- Лапласа.

1. Магнітне поле прямого та колового
провідників зі струмом.
2. Взаємодія струмів.
3. Закон повного струму, магнітне поле
соленоїда. Вихровий характер магнітного
поля.
4. Робота при переміщенні провідника зі
струмом в магнітному полі. Енергія
провідника зі струмом.