Газовые смеси

1.

1

2. ГАЗОВЫЕ СМЕСИ

3.

Давление является результатом совокупного воздействия
на поверхность молекул газа.
Если речь идет о смеси газов, молекулы которых имеют
разные массы и движутся с разными скоростями, то ее
давление будет складываться из давлений составляющих ее
газов. В связи с этим закон Дальтона формулируется
следующим образом: «Давление смеси газов равно сумме
парциальных (собственных) давлений ее компонентов»:
i n
p pi
i 1
Таким образом, при удалении из смеси одного из ее
компонентов давление понижается на величину, определяемую
массой его молекул, их числом и скоростью движения, а при
введении в смесь дополнительного компонента ее давление
возрастает.
3

4. Парциальный объем компонента смеси

4

5.

Для всех компонентов одинаковыми являются объем V и
температура смеси T. При этом каждый из газов воздействует на
поверхность своим собственным давлением pi. Если каким-либо
образом удалить из объема все газы, кроме одного, его давление
будет равно pi. Уменьшая при неизменной температуре смеси T
объем, можно поднять давление газа до исходного значения
давления смеси p. В случае T=idem справедливо уравнение БойляМариотта
(1)
piV pVi ,
где Vi
– объем, который занимает отдельный компонент при
температуре и давлении смеси. Этот объем называется
парциальным.
5

6.

Из выражения (1) имеем
pi
Vi V
p
Просуммировав парциальные объемы всех n компонентов смеси,
получаем
n
n
Vi V
1
pi
1
p
.
Но в соответствии с законом Дальтона стоящая в числителе сумма
равна давлению смеси, а потому
n
Vi V
,
(2)
1
то есть сумма парциальных объемов компонентов равна
объему смеси.
6

7. Задание состава смеси

7

8.

Состав
смеси
задается
долями
ее
компонентов,
представляющими собой отношение количества отдельного
газа к количеству смеси. В зависимости от того, чем именно
оценивается количества компонентов и смеси в целом,
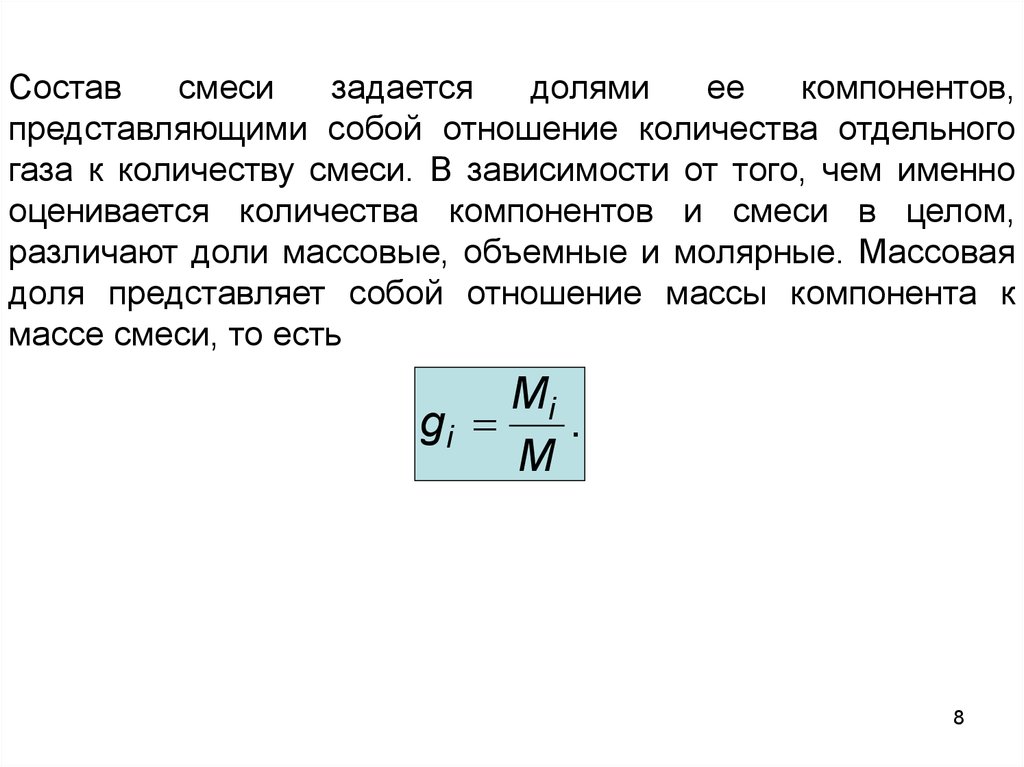
различают доли массовые, объемные и молярные. Массовая
доля представляет собой отношение массы компонента к
массе смеси, то есть
Mi
gi
.
M
8

9.

Аналогично
каждая
объемная
доля
определяются
соотношением парциального объема отдельно взятого
компонента и объема смеси:
Vi
ri .
V
Молярная доля находится как отношение
Ni
ni
,
N
где N – суммарное количество молей смеси.
9

10.

Молярные доли численно равны объемным, что следует из закона
Авогадро, в соответствии с которым при одинаковых
термодинамических условиях объем моля любого газа есть
величина постоянная. Умножая последнее выражение на объем
одного моля при давлении и температуре смеси, получаем
ni
N iV
NV
Vi
ri ,
V
что доказывает равенство молярных и объемных долей.
При расчетах обычно используются объемные доли ri.
Следует помнить, что в общем случае массовые доли
не равны объемным.
10

11.

Пример 1: Определить значения массовых долей компонентов
смеси, состоящей из 4-х кг двуокиси углерода, 4-х кг азота и 2-х кг
водорода.
Решение: Массовые доли определяются отношением массы
компонента к массе смеси ( g i M i M ). Масса смеси равна сумме
масс компонентов, а потому
M MCO 2 MN 2 MH 2 4 4 2 10 [кг]
Массовая доля двуокиси углерода равна
Аналогично
g N2
M N2
4
0,4 и
M
10
gCO 2
gH 2
MCO 2
M
4
0,4.
10
MH 2
2
0,2
M
10
Поскольку сумма долей равна единице, то массовую долю водорода
можно было находить и как разность
gH 2 1 gCO 2 gN2 1 0,4 0,4 0,2

12. Кажущаяся молярная масса смеси

12

13.

Для использования уравнения состояния необходимо знать газовую
постоянную смеси, которая определяется при известном значении μ
смеси как отношение R 8314 / .
.
Но смесь состоит из различных газов, молекулярные массы которых
в общем случае разнятся. В связи с этим используется понятие
усредненной, так называемой «кажущейся» молекулярной массы.
Усреднение производится в предположении, что количество
«кажущихся» молекул равно количеству реальных молекул
n
отдельных газов ( N N ) , а их суммарная масса равна массе
i
n
1
смеси ( M Mi ).
1
13

14.

Имея в виду, что масса равна произведению количества молей на
n
массу одного моля, выражение M Mi можно переписать как
n
1
N (Ni i )
Если разделить это равенство на 1общее количество молей
Ni
то получаем i , где отношение
N
1
n
Ni
N
есть
(объемная) доля, а потому окончательно имеем .
n
i r i
N,
молярная
(3)
1
Это выражение позволяет определять кажущуюся массу смеси в том
случае, когда ее состав задается объемными долями.
14

15.

Для нахождения кажущейся массы смеси при задании ее состава
n
массовыми долями воспользуемся выражением N Ni , подставляя
1
в него количества молей, определяемые как отношения массы газа к
n M
M
массе одного моля. В этом случае
.i
1 i
1 n Mi 1
После деления на суммарную массу смеси получаем .
Но отношение
а потому
1
M i
Mi
представляет собой массовую долю gi i–го газа,
M
.
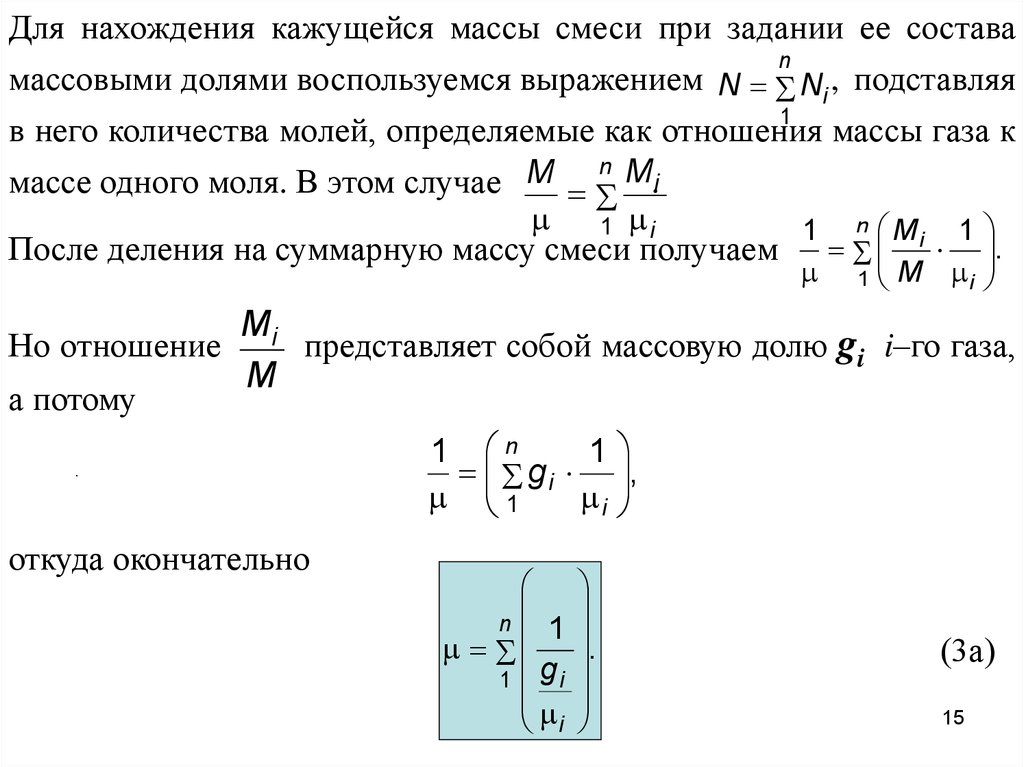
откуда окончательно
1 n
1
g i ,
1
i
n
1
1 gi
i
.
(3а)
15

16.

Пример 2: Определить кажущуюся массу смеси заданного в
предыдущем примере состава, и ее газовую постоянную.
Решение: Используя выражение (3а), для рассматриваемого случая
можем записать
gCO 2
CO 2
1
gN2
N 2
gH
2
H 2
1
8,105 [кг/кмоль]
0,4 0,4 0,2
44 28
2
Газовая постоянная определяется отношением R 8314 , а
потому
R
8314
Дж
1025,8 [
].
8,105
кг К
16

17. Газовая постоянная смеси

17

18.

Чтобы найти зависимость для определения газовой постоянной
смеси при известном ее массовом составе, в уравнение (3а)
подставим молекулярную массу, полученную из величины
универсальной газовой постоянной
8314
.
R
(4)
8314 n 1
В этом случае имеем R R g , или окончательно
1
i i
8314
n
R Ri g i .
(5)
1
18

19.

При подстановке μ из (4) в выражение (3)
получаем
n
i ri
1
8314
8314
ri .
R
1 Ri
n
Отсюда величина газовой постоянной при известном объемном
составе смеси находится как сумма отношений
1
R n
Ri
1 ri
(5а)
Естественно, при известном значении кажущейся молярной массы
газовую постоянную смеси целесообразнее определять как
R
8314
.
Следует отметить, что значение газовой постоянной влажного
воздуха (который является смесью сухого воздуха и паров воды)
есть величина переменная, зависящая от его относительной
19
влажности.

20.

Пример 3: Проверить правильность определенного в примере
2 значения газовой постоянной смеси с использованием
зависимости (5).
Решение: Предварительно определяем газовые постоянные
компонентов смеси
RCO 2
R H2
8314
Дж
8314 8314
Дж
296,93 [
] и
188,95 [
], RN2
28
кг К
CO 2
44
кг К
8314
Дж
4157 [
] . Делая подстановку в (5), получаем
2
кг К
R gCO 2 RCO 2 g N 2 RN 2 g H 2 RH 2
Дж
]
кг К
Таким образом, газовая постоянная смеси равна сумме
произведений газовых постоянных отдельных ее компонентов на
20
соответствующие массовые доли.
0,4 188,95 0,4 296,93 0,2 4157 1025,8 [

21. Удельный объем и плотность смеси

21

22.

n
В соответствии с выражением V Vi (2) объем смеси равен сумме
парциальных объемов компонентов 1смеси.
Учитывая, что объем равен произведению массы на удельный объем
(объем одного килограмма), получаем
n
Mv Mi v i .
1
Так как отношение M i M представляет . собой массовую долю
отдельного компонента, после деления полученного равенства на
массу смеси можем записать
n
(6)
v g i v i .
1
то есть удельный объем газовой смеси равен сумме произведений
удельных объемов компонентов при параметрах смеси на
22
соответствующие массовые доли.

23.

Выражение для определения удельного объема смеси при
известном объемном составе находится из равенства массы смеси
сумме масс компонентов. Поскольку v V M и, следовательно,
n
M V v , после подстановки в равенство M Mi получаем
1
n
Vi
V
v
1 vi
Деля это равенство на объем смеси V, представляем его в виде
Но
отношение
Vi
V
1 n Vi
v 1 Vv i
.
равно объемной доле отдельного компонента,
а потому
vi
1
n r
i
1 vi
.
(6а)
23

24.

Аналогично находятся и выражения для определения плотности
смеси. Поскольку плотность есть масса единицы объема, и в любом
случае масса может быть представлена произведением объема на
n
n
плотность, выражение M Mi можно переписать как V Vi i. .
1
1
После деления этого равенства на объем смеси V имеем
Vi
i
1 V
n
или
n
ri i ,
(7)
1
то есть – плотность газовой смеси равна сумме произведений
плотностей отдельных компонентов (при параметрах смеси) на
соответствующие объемные доли.
24

25.

Если состав смеси задается массовыми долями, то выражение для
определения ρ находится из равенства (2). Поскольку плотность
есть масса единицы объема M V и, следовательно, V M ,
n
после подстановки в V Vi получаем
1
M n Mi
.
1 i
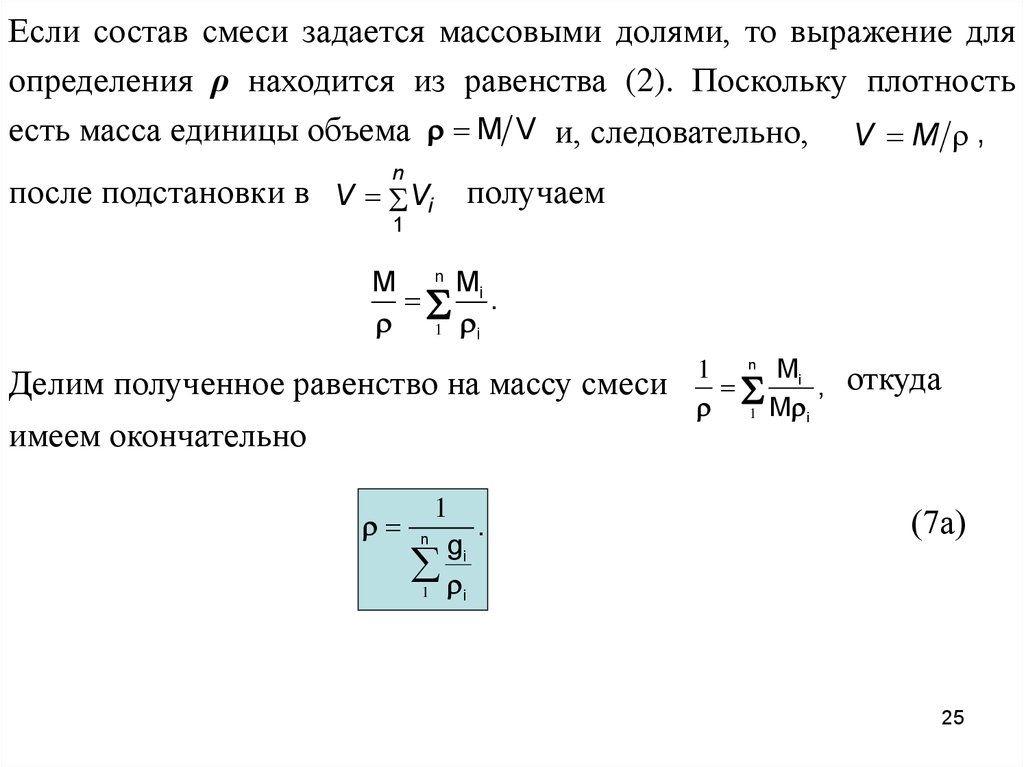
Делим полученное равенство на массу смеси
имеем окончательно
1
n
.
gi
1
i
1 n Mi
,
1 M i
откуда
(7а)
25

26.

Пример 4: Определить значения удельного объема и плотности
смеси состава, указанного в примере 1, при давлении 1 бар и
температуре 270С.
n
Решение. Чтобы воспользоваться зависимостьюv g i v i , необхо1
димо предварительно найти значения удельных объемов
компонентов смеси при ее параметрах.
Аналогичн
RCO 2 T 188,95 300
кг
v CO 2
0,56685 [ 3 ].
5
о
p
1 10
м
v N2
296,93 300
1 10
5
0,8908 [
кг
м
и
]
3
vH2
После подстановки в (6) получаем
4157 300
1 10
5
12,471 [
кг
м
3
]
v gCO 2 v CO 2 g N 2 v N 2 g H 2 v H 2
0,4 0,56685 0,4 0,8908 0,2 12,471 3,077 [
кг
м
3
].
Проверим результат, используя значение газовой постоянной смеси,
полученное в примере 3
v
RT 1025,8 300
кг
3
,
077
[
].
5
3
p
1 10
м
26

27. Взаимный пересчет массовых и объемных долей

27

28.

Часто возникает задача перевода массовых долей в объемные и
наоборот. Учитывая, что массовая доля равна отношению
g i M i M, подставляем в числитель и знаменатель массы,
представляя их произведением количеств молей N на
соответствующие молекулярные массы μ. В этом случае можно
записать
gi
Ni i
.
N
Отношение N i N в этом выражении равно объемной доле, в связи
с чем его можно переписать как
ri i ,
(8)
gi
n
или, с использованием i ri
1
gi
ri i
n
i r
1
.
(8а)
28

29.

Аналогично
получаем
и
выражения
для
определения
объемных/молярных долей по известным массовым. Для этого
записываем исходное выражение ri Ni / N и подставляем в него
количества молей N, определяемые как отношения массы газа к
массе одного моля
Mi
Ni
i
ri
.
M
N
После деления числителя и знаменателя на массу смеси M получаем
.
gi
i , так как g M M .
ri
i
i
1
29

30.

Следовательно, расчетная формула приобретает вид
gi
ri .
i
n
С учетом выражения
1
в виде
1
gi
i
(9)
(3а) ее также можно представить
gi
i
ri n
.
gi
1
i
(9а)
30

31.

Пример 5: Определить объемный состав рассматриваемой в 1
смеси.
Решение. Используя найденное в примере 2 значение кажущейся
молекулярной массы (μ = 8,105 кг/кмоль) в соответствии с
выражением (9) получаем:
rCO 2
rN 2
rH 2
gCO 2
CO 2
gN2
N 2
gH2
H 2
0,4
8,105
0,0737,
44
8,105
8,105
0,4
0,1158,
28
0,2
0,8105.
2
rCO 2 rN 2 rH 2 1.
31

32.

В связи с тем, что сумма долей всегда равна единице, последнее
слагаемое можно было бы определить и как разность
rH 2 1 rCO 2 rN 2 1 0,0737 0,1158 0,8105.
Нетрудно видеть, что объемные доли существенно отличаются от
массовых. Так, если массовая доля водорода составляла g H 0,2,
2
то объемная доля превосходит ее более чем в 4 раза ( rH 2 0,8105 ).
Соответственно при массовой доле 0,4 двуокись углерода
характеризуется в рассматриваемой смеси величиной rCO 2 0,0737.
При изменении параметров смеси ее состав (массовый и
объемный) остается постоянным.
32

33. Давление компонентов смеси

33

34. То есть, парциальное давление компонента определяется произведением давления смеси на соответствующую объемную / мольную долю.

В случае задания состава смеси объемными долями парциальные
давления могут находиться с использованием приведенного в
начале раздела выражения (1)
piV pVi .
Из него следует
Vi
pi p
V
или
pi pr i
.
(10)
То
есть,
парциальное
давление
компонента
определяется произведением давления смеси на
соответствующую объемную / мольную долю.
34

35.

Если записать уравнение состояния 2 раза – для Mi кг отдельного
компонента и для M кг смеси, то после деления первого из них на
второе можно получить выражения для определения парциального
давления компонента при задании состава смеси массовыми
долями. Действительно,
piV Mi RiT
pV MRT.
Тогда частное от деления равно
pi g i
pi M i Ri
p
M R
Ri
R
или
(10а)
В связи с тем, что значения газовых постоянных обратно
пропорционально молекулярным массам компонентов, последнее
равенство можно переписать и следующим образом
pi g i
.
i
(10 б)
35

36.

Пример 6: Определить парциальные давления компонентов
рассматриваемой в примере 1 смеси.
Решение. Значения парциальных давлений могут определяться с
использованием любых из полученных выше зависимостей – (10),
(10а) или (10б). Для примера воспользуемся выражением (10) для
определения pCO , выражением (10а) для нахождения pN , а ве2
2
личину pH 2 найдем по зависимости (10 б). В этом случае
pCO 2 p rCO 2 1 0,0737 0,0737 [бар]
,
pN 2 g N 2
RN 2
R
0,4
296,93
0,1158 [бар]
1025.8
(этот же результат получим и с использованием выражения (10)):
pN 2 p rN 2 1 0,1158 [бар]
36

37.

Парциальное давление водорода определим по выражению (10 б)
pH 2 g H 2
8,105
0,2
0,8105 [бар] .
H 2
2
Проверка – в соответствии с законом Дальтона сумма парциальных
давлений должна равняться давлению смеси:
p pCO 2 pN 2 pH 2 0,0737 0,1158 0,8105 1 [бар].
Таким образом, сумма подсчитанных с использованием разных
зависимостей парциальных давлений оказалась равной давлению
смеси, что свидетельствует о
полученных выражений.
правомерности
использования
37

38. Теплоемкость газовой смеси

38

39.

Теплоемкость – количество теплоты, необходимое для
изменения температуры единицы количества вещества на 1 К.
Массовая теплоемкость смеси c есть количество теплоты q,
необходимое для изменения температуры каждого из компонентов
1 кг смеси на 1 К, то есть
n
q c Qi
(11)
1
M
Здесь q – количество
теплоты, необходимое для нагрева 1 кг смеси
на 1 К, а Qi – количества теплот, необходимые для нагрева на 1 К
n
масс отдельных компонентов, меньших 1 кг. Но M 1 кг M i
и после деления этого равенства на равную 1 кг массу смеси
1
M
n
получаем 1 g i .
1
Следовательно, масса каждого из компонентов 1 кг смеси
численно равна его массовой доле.
39

40.

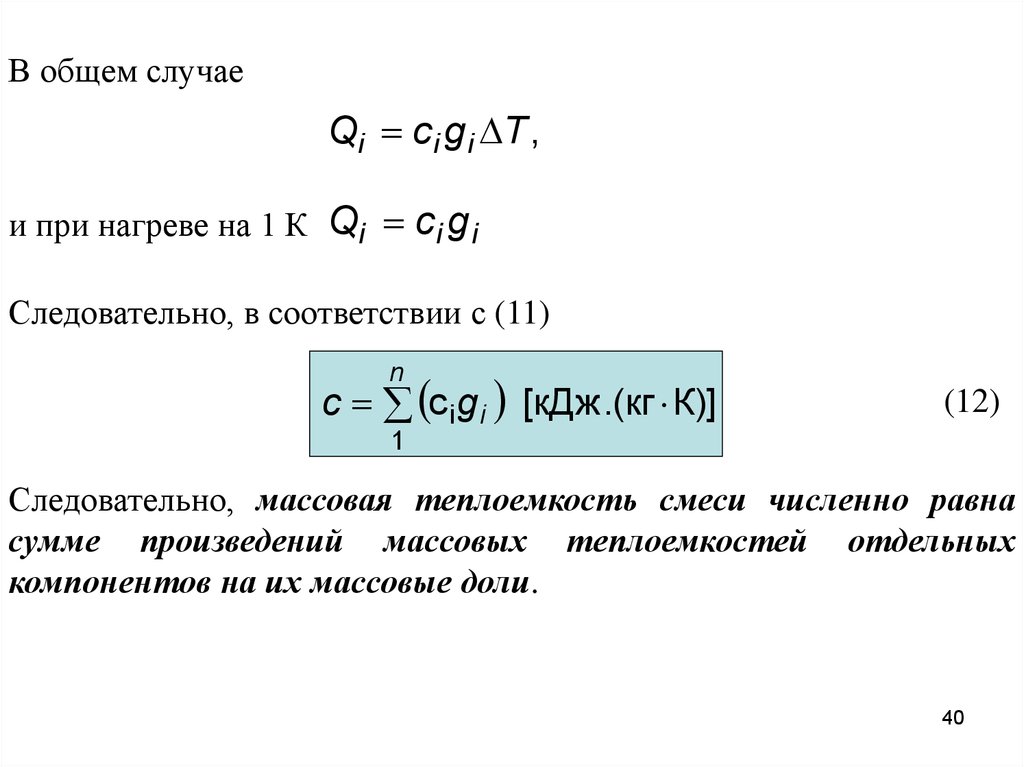
В общем случае
Qi c i g i T ,
и при нагреве на 1 К Qi c i g i
Следовательно, в соответствии с (11)
n
с c ig i [кДж.(кг К)]
(12)
1
Следовательно, массовая теплоемкость смеси численно равна
сумме произведений массовых теплоемкостей отдельных
компонентов на их массовые доли.
40

41.

Пример 7. Определить среднюю массовую теплоемкость
смеси заданного в первом примере состава при постоянном
давлении и постоянном объеме, если теплоемкости
компонентов равны соответственно
c pCO 0,815 [кДж/(кг К)] и
c pN 1,03 [кДж/(кг К)] ,
2
2
c pH 14,19 [кДж/(кг К)]
2
Решение. Из выражения (12) получаем
c p c pN g pN c pCO g pCO c pH g pH
2
2
2
2
2
2
1,03 0,4 0,815 0,4 14,19 0,2 3,58 [кДж/(кг К)] .
В соответствии с уравнением Майера массовая теплоемкость при
постоянном объеме равна cv c p R .
Используя найденное в примере 3 значение газовой
постоянной
R 1025,8 [ Дж/(кг К)] ), получаем
(
cv 3,58 1,03 2,56 [кДж/(кг К)]
41

42.

Объемная теплоемкость смеси c есть количество теплоты q,
необходимое для изменения температуры каждого из компонентов
1 м3 смеси на 1 К, что описывается уравнением (11) n
q Qi, где q c V T или, при V 1 м3 и T 1K , q c .
1
Количество теплоты, необходимое для нагрева i-го компонента
определяется равенством Qi c i Vi T или, при нагреве на 1 К,
n
Qi c i Vi . Но в соответствии с равенством (2) V Vi 1 м3 , и после
n
1
1
r
,
i так как Vi V ri .
деления на объем смеси V получаем
1
Следовательно, парциальные объемы компонентов 1 м3 смеси
численно равны их объемным долям. В этом случае можно записать
n
n
n
1
1
1
q c Qi c i Vi c i ri [кДж /(м3 K)] ,
то есть окончательно
n
c c i ri
1
(13)
– объемная теплоемкость смеси газов равна сумме произведений
объемных теплоемкостей ее компонентов на соответствующие
42
объемные доли.

43.

Пример 8. Определить среднюю объемную теплоемкость смеси
заданного в первом примере состава при постоянном давлении и
постоянном объеме, если объемные теплоемкости компонентов
равны соответственно
3
3 ,
c
1
,
6
[
кДж/(м
К)] и
pCO
c p 1,29 [кДж/(м К)]
2
N2
c pH 1,25 [кДж/(м3 К)] .
2
Решение. В соответствии с выражением (15) получаем
n
c p c i ri c pN r pN c pCO r pCO c pH r pH
1
2
2
2
2
2
2
1,29 0,116 1,62 0,074 1,25 0,811 1,28 [кДж/(м3 К)].
.
Так как c есть теплоемкость 1 м3 или кг вещества, то
теплоемкость 1 кг (массовая теплоемкость) может быть найдена из
соотношения c c / . Следовательно
c p
1,28
cp
3,58 [кДж/(кг К)].
0,357
43

44.

Сравнивая полученный ответ с ответом примера 7, приходим к
выводу о правильности решения.
Значение теплоемкости смеси при постоянном объеме найдем с
использованием уравнения Майера cv c p R. Если домножить
это уравнение на значение плотности объема смеси, то в результате
cv cv c p R
получим объемную теплоемкость
или
cv c p R 1,28 0,357 1,026 0,91 4 [кДж/(м 3 К )].
При нормальных физических условиях плотность определяется
выражением 22,4. В связи с этим произведение R можно
представить в виде
R
8314 8314
371,2 [ Дж/(м3К )].
22,4
22,4
44

45.

Это выражение численно равно работе, совершаемой одним м3
смеси при повышении температуры на 1 К.
Для проверки результатов расчета, разделив полученное значение на
величину плотности смеси, получаем
cv 0,914
cv
2,56 [кДж/(кг К],
0,357
что согласуется с ответом
правильность решения.
в примере 7 и подтверждает
45

46.

Молярную теплоемкость смеси можно определить исходя из тех же
посылок, что и теплоемкости массовую и объемную. Так,
суммарное количество молей смеси равно сумме молей отдельных
n
ее компонентов. После деления равенства N Ni количество
1
молей N 1 получаем, что один моль смеси численно равен сумме
молярных или равных им объемных долей компонентов смеси (так
n
как Ni N ni ri ). Отсюда следует 1 ri .
1
Для нагревания одного моля смеси на 1 К необходимо нагреть на 1
К и каждые ri молей смеси, то есть –
n
c c i ri .
(14)
1
Таким образом, молярная теплоемкость смеси равна сумме
произведений молярных теплоемкостей ее компонентов на
соответствующие молярные/объемные доли.
46

47.

Пример 9. Определить среднюю молярную теплоемкость смеси
заданного в первом примере состава при постоянном давлении и
постоянном объеме, если теплоемкости компонентов равны
соответственно
c pN 29,02 [кДж/(моль К)] ,
c pCO 33,5 [кДж/(моль К)] и
2
2
c pH 28,66 [кДж/(моль К)].
2
Решение. В соответствии с равенством (16) имеем
c p c pN rN 2 c pCO rCO 2 c pH rH 2
2
2
2
29,02 0,1158 33,5 0,0737 28,66 0,8105 29,06 кДж /( моль К ) .
В качестве проверки при известном значении молекулярной массы
смеси (пример 2) определим значение массовой теплоемкости
cp
c p
29,06
3,58 [кДж/кг К)],
8,105
что полностью согласуется с результатами, полученными в примере
№ 7.
47

48.

Используя уравнение Майера для 1 моля рабочего тела, получаем
cv c p R 29,06 8,314 20,746 кДж /(моль К ) .
После деления полученного значения на массу моля смеси получаем
массовую теплоемкость при постоянном объеме
cv 20,75
cv
2,56 [кДж/кг К)].
8,105
Эта же величина была получена и в примере № 8, что подтверждает
правильность полученных выше зависимостей.
48

49.

Учитывая, что большинство рабочих тел является газовыми
смесями, полученные выше выражения позволяют определять
необходимые для проведения расчетов и анализа:
• массовый и объемный (молярный) состав смеси,
• кажущуюся молярную массу,
• газовую постоянную,
• удельный объем и плотность смеси,
• значения парциальных давлений
и
объемов
компонентов
смеси,
• теплоемкости смеси.
49

50.

Рекомендуемая литература
а) Основная
1. Теплотехника: учебник для студ. высш. учебн. заведений/ М.Г.Шатров,
И.Е.Иванов, С.А.Пришвин и др.; под ред. М.Г.Шатрова. – М. : Издательский
центр «Академия», 2011. – 288 с.
2. Иванов, И.Е. Теплотехника: конспект лекций/ И.Е.Иванов, В.Е.Ерещенко;
МАДИ (ГТУ). – М., 2009. – 139 с.
б) Дополнительная
1. Теплотехника: Учебник для вузов /В.Н. Луканин, М.Г. Шатров, Г.М. Камфер и
др.; под ред. В.Н. Луканина – 7-е изд., стер. – М.: Высш шк. 2009 – 671 с.:ил.
2. Теплотехника: учебник для студентов вузов/ под ред. В.И. Крутова – М.:
Машиностроение. 1991 – 432 с.: ил.
3. Алексеев Г. Н. Общая теплотехника: Учебное пособие.- М.: Высш. шк., 1980 –
552 с.
4. В. В. Нащёкин. Техническая термодинамика и теплопередача: Учебн. пособие
для вузов –3-е изд.-М.: Высш. шк., 1980 – 469с.
50