Похожие презентации:
Векторы в пространстве. Сложение векторов
1. Векторы в пространстве. Сложение векторов.
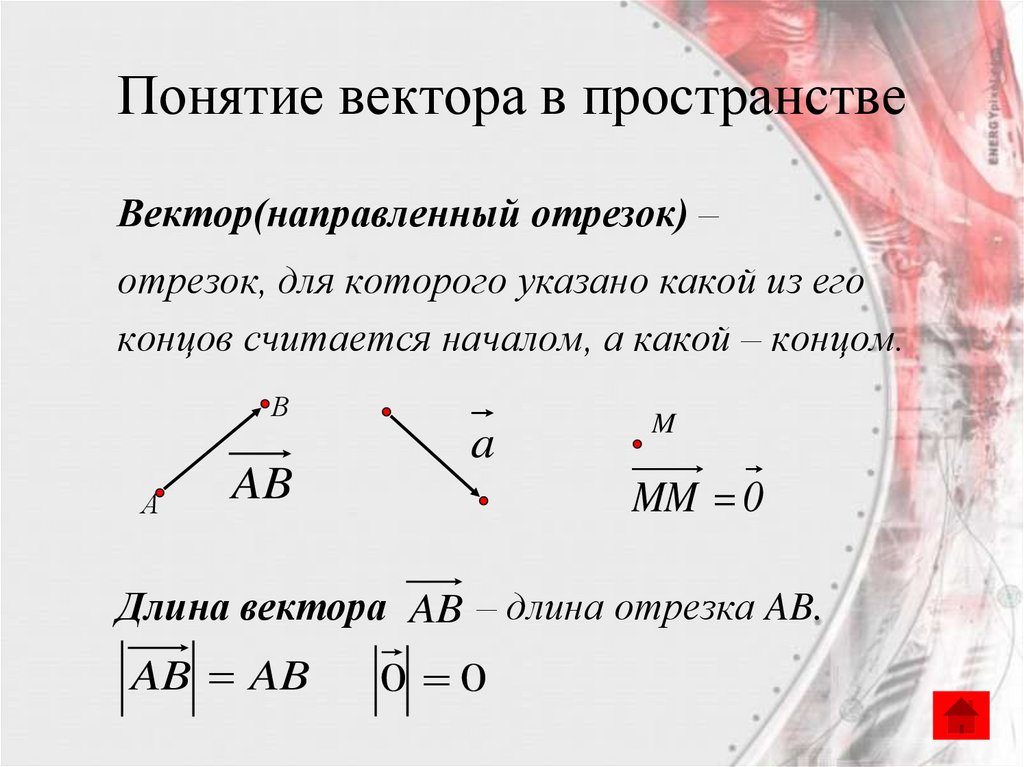
2. Понятие вектора в пространстве
Вектор(направленный отрезок) –отрезок, для которого указано какой из его
концов считается началом, а какой – концом.
В
А
AB
a
M
MM 0
Длина вектора AB – длина отрезка AB.
AB AB
0 0
3. Коллинеарные векторы
Два ненулевых вектора называютсяколлинеарными, если они лежат на одной
прямой или параллельных прямых.
Среди коллинеарных различают:
• Сонаправленные векторы
• Противоположно направленные векторы
4. Сонаправленные векторы
Сонаправленные векторы - векторы, лежащиепо одну сторону от прямой, проходящей через их
начала.
a
a b
b
Нулевой вектор считается сонаправленным с
любым вектором.
• Равные векторы
5. Равные векторы
Равные векторы - сонаправленные векторы,длины которых равны.
a
a b a b, a b
b
От любой точки можно отложить вектор,
равный данному, и притом только один.
6. Противоположно направленные векторы
Противоположно направленные векторы –векторы, лежащие по разные стороны от прямой,
проходящей через их начала.
a
a b
b
Противоположные векторы
7. Противоположные векторы
Противоположные векторы – противоположнонаправленные векторы, длины которых равны.
a
a b a b, a b
b
Вектором, противоположным нулевому,
считается нулевой вектор.
8. Сложение векторов
Правило треугольника
Правило параллелограмма
Правило многоугольника
Правило параллелепипеда
Свойства сложения
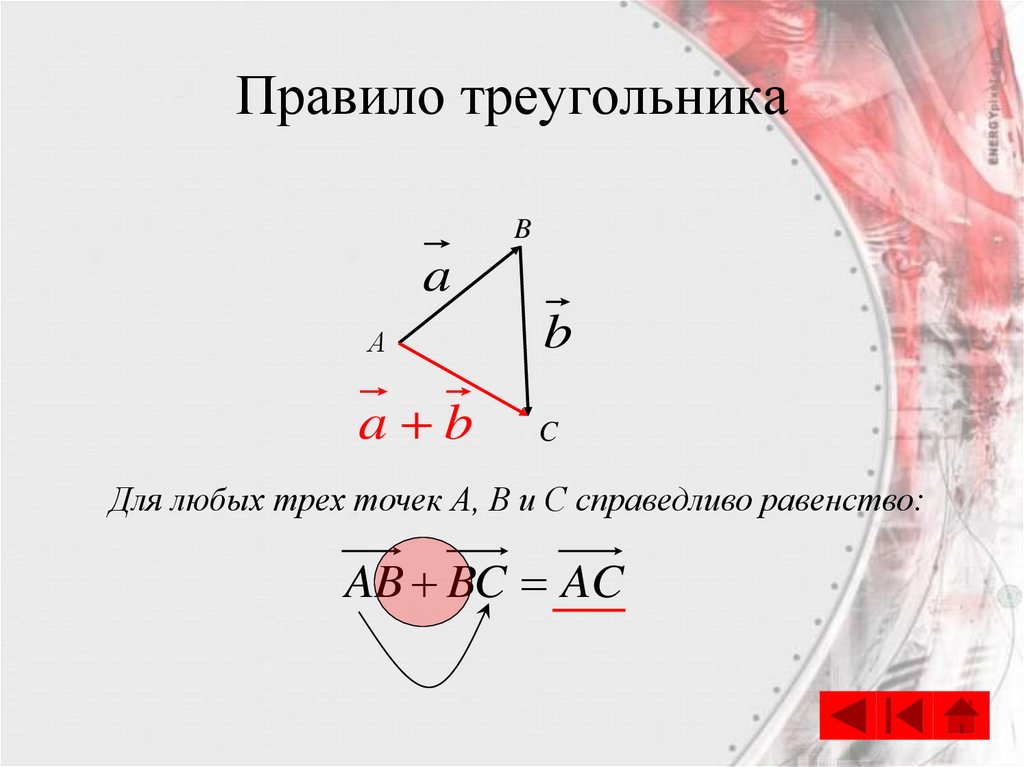
9. Правило треугольника
Для сложения двух векторов необходимо :1. отложить от какой нибудь точки А вектор
AB, равный а
2. от точки В отложить вектор BC , равный b
3. вектор AC называется суммой векторов a и b
B
a
a
А
b
a b
b
C
10. Правило треугольника
Ba
А
a b
b
C
Для любых трех точек А, В и С справедливо равенство:
AB BC AC
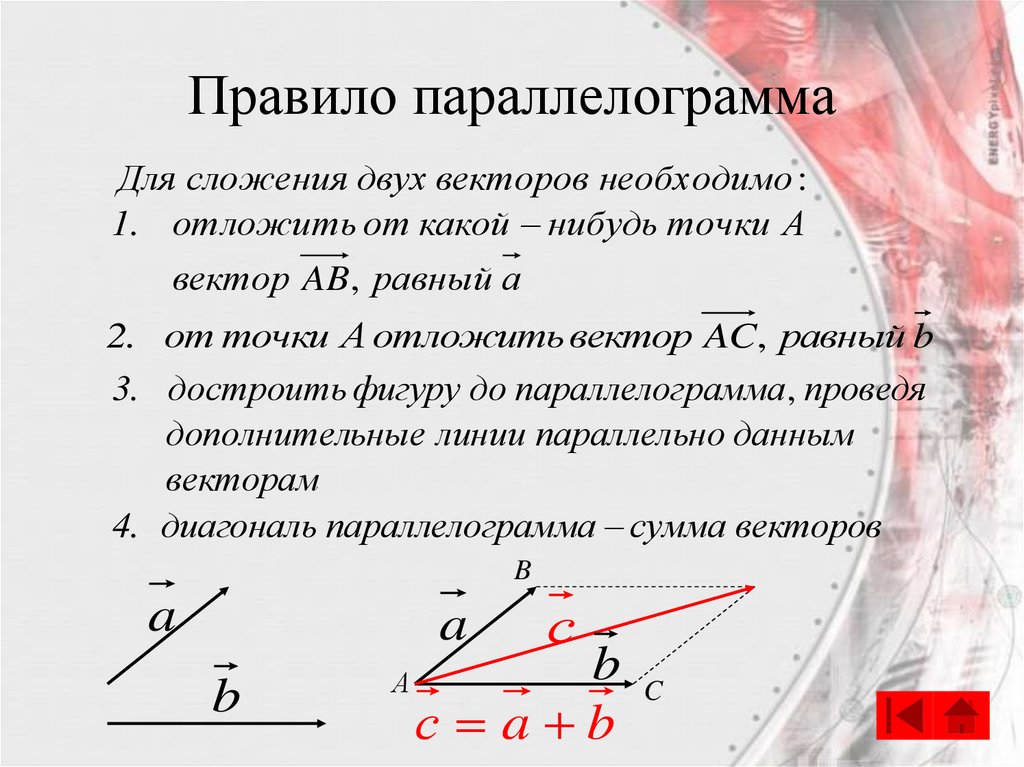
11. Правило параллелограмма
Для сложения двух векторов необходимо :1. отложить от какой нибудь точки А
вектор AB, равный а
2. от точки А отложить вектор AC, равный b
3. достроить фигуру до параллелограмма , проведя
дополнительные линии параллельно данным
векторам
4. диагональ параллелограмма сумма векторов
B
a
a
b
А
с
b
с a b
C
12. Свойства сложения
Для любых векторов a , b и c справедливыравенства :
a b b a
a b с а b с
переместительный закон
сочетательный закон
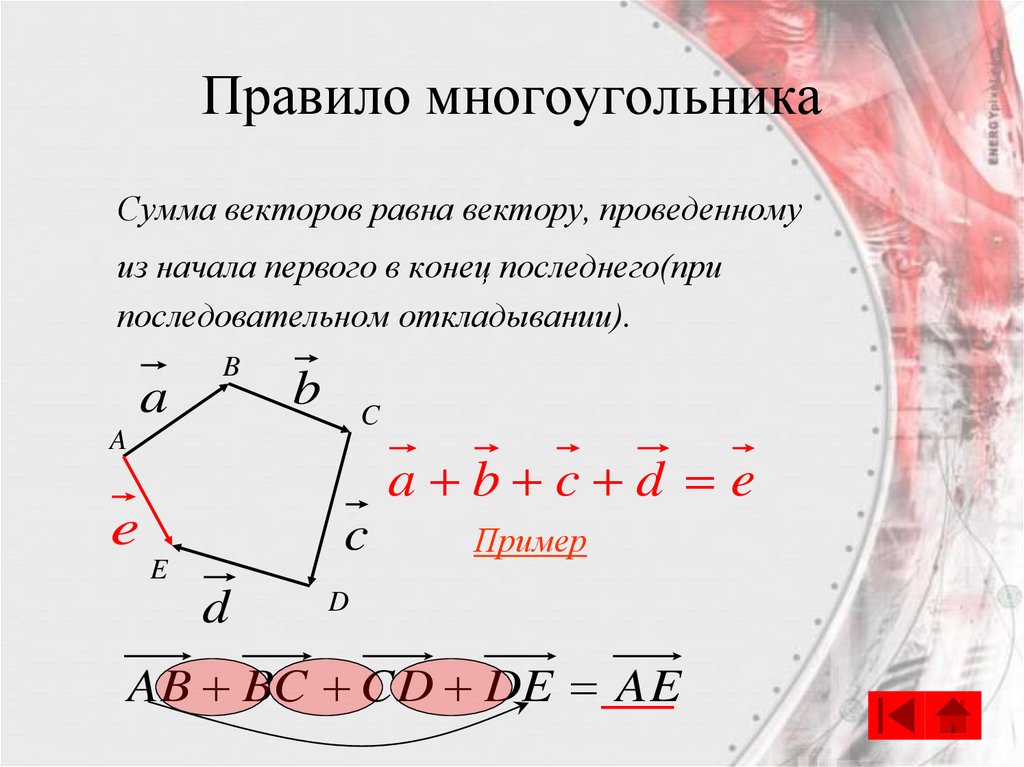
13. Правило многоугольника
Сумма векторов равна вектору, проведенномуиз начала первого в конец последнего(при
последовательном откладывании).
a
B
b
C
A
a b c d e
e
c
E
d
Пример
D
AB BC CD DE AE
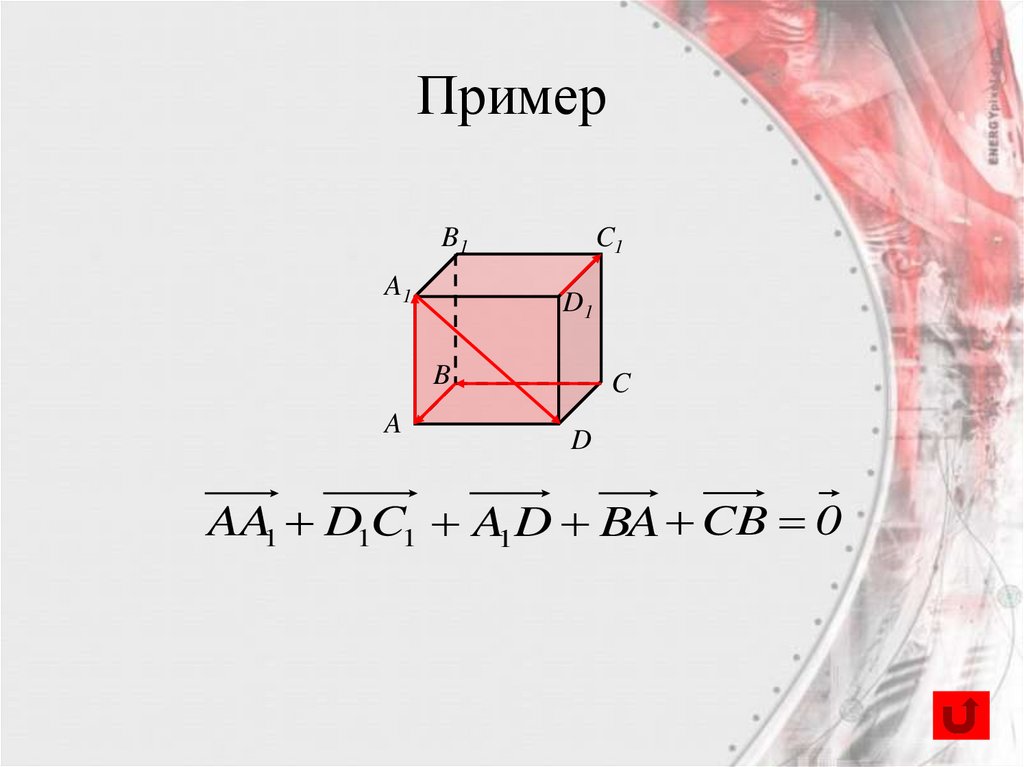
14. Пример
B1A1
C1
D1
B
A
C
D
AA1 D1C1 A1 D BA CB 0
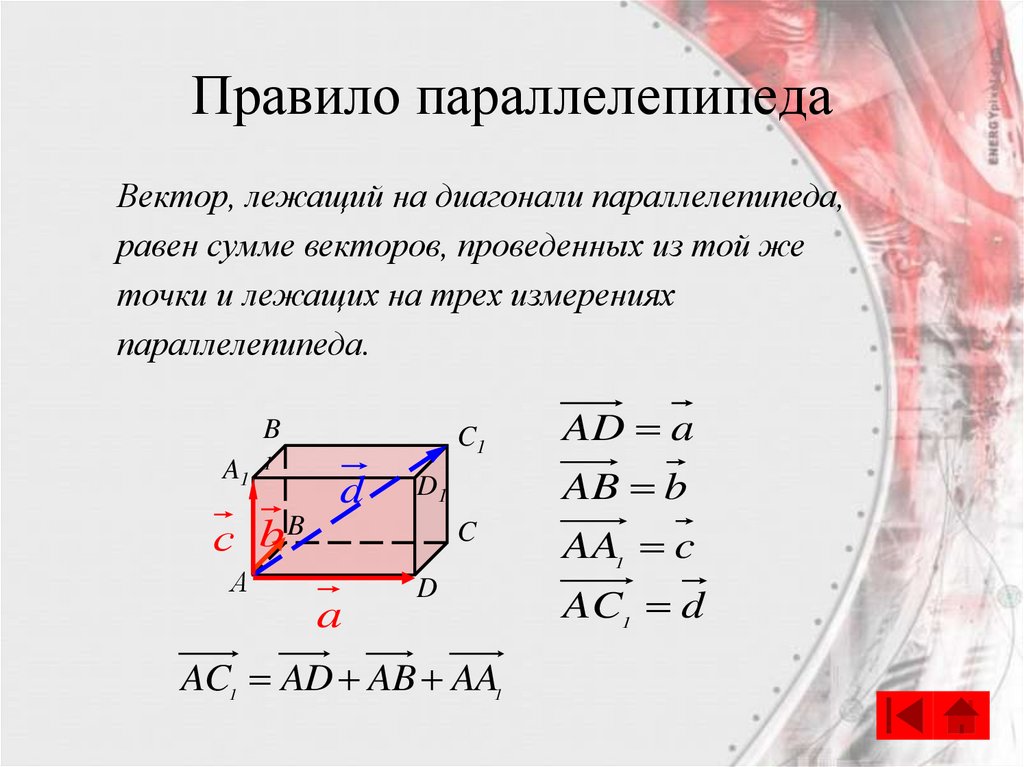
15. Правило параллелепипеда
Вектор, лежащий на диагонали параллелепипеда,равен сумме векторов, проведенных из той же
точки и лежащих на трех измерениях
параллелепипеда.
B
A1
C1
1
d
AB b
D1
с bB
C
А
a
AD a
D
AC1 AD AB AA1
AA1 c
AC1 d
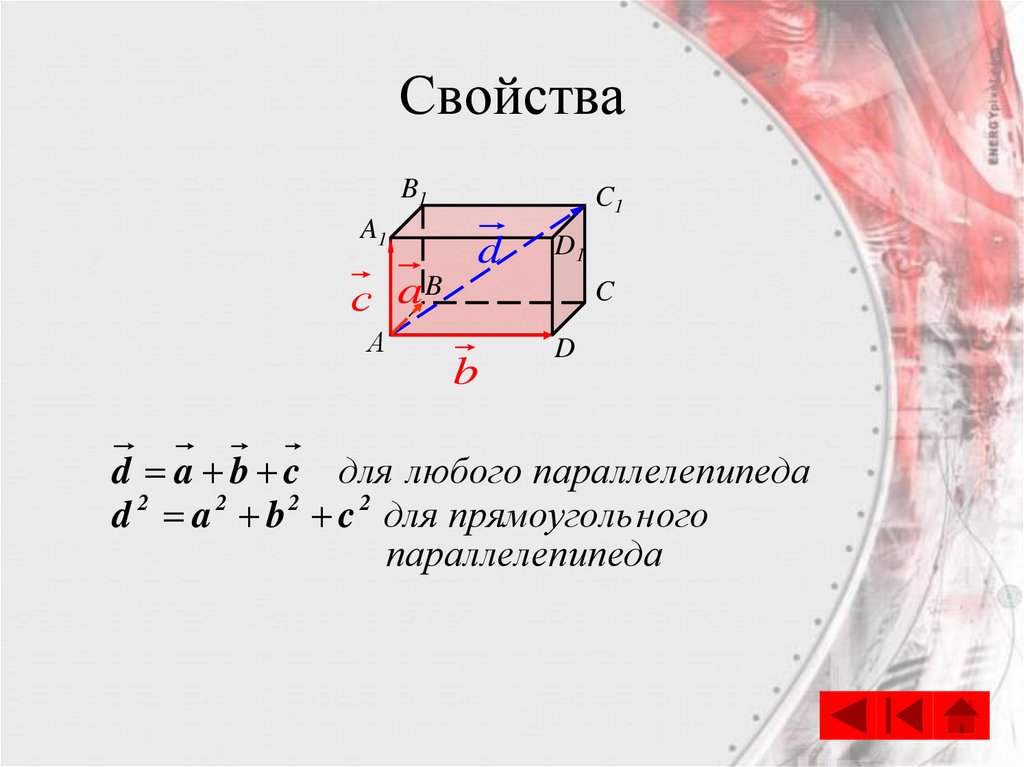
16. Свойства
B1A1
C1
d
D1
с aB
А
C
b
D
d a b c для любого параллелепипеда
d 2 a 2 b 2 c 2 для прямоуголь ного
параллелепипеда









 Математика
Математика








