Дистанционное зондирование окружающей среды

1. Дистанционное зондирование окружающей среды Сплайн-интерполяция

Профессор Кузнецов Анатолий Дмитриевич
Доцент Сероухова Ольга Станиславовна
Российский государственный
гидрометеорологический университет

2.

Во многих прикладных науках задачи интерполяции данных
играют значительную роль: от точности интерполяции
исходных данных зависят последующие метеорологические и
гидрологические прогнозы.
Значения таких параметров как скорость ветра, температура
или осадки часто измеряются на метеорологических станциях,
расположенных неравномерно на больших расстояниях друг от
друга, поэтому задача вычисления этих параметров на
заданном участке сводится к интерполяции одномерных и
двумерных полей, заданных точечными значениями.
Наряду с полиномиальной интерполяцией, которая не всегда
при большой размерности подлежащих обработке табличных
данных, для графического представления этих данных может
быть использован метод сплайн-интерполяции.
Он был «изобретен» чертежниками, когда для проведения
плавной линии через узловые точки они использовали
металлическую линейку. Название метода – сплайн, произошла
от англ. слова splaine – линейка.

3.

Сплайны являются одним из наиболее распространенных
средств вычислительной математики для решения прикладных
задач.
Популярность сплайнов объясняется, в
причинами.
основном, двумя
Во-первых, сплайны представляют собой чрезвычайно гибкое
средство решения разнообразных задач интерполяции и
аппроксимации функций.
Во-вторых, алгоритмы построения сплайнов легко и эффективно
реализуются на персональных компьютерах.

4.

Рассмотрим возможности реализации этого метода при
использовании одинарных кубических сплайнов. Для этого
необходимо
решить
следующую
задачу
построить
интерполяционный кубический сплайн на некотором отрезке, на
котором задана функция так, чтобы
g (x k ) g k
Здесь xk - узлы интерполяции, а интерполяционная функция
имеет следующий вид:
g(x) = a x3 + b x2 + c x + d .
(1)

5.

Коэффициенты a, b, c и d определяются исходя из выполнения
следующих условий:
1) g (a) = g (b) = 0 (естественные граничные условия);
2) g (xk) = gk (совпадение сплайна с табличными значениями в
узлах);
3) g(x) , g (x) , g (x) являются непрерывными функциями (условие
“сплайна”).

6.

Обозначим:
hi = xi - xi-1,
g (xi) = mi ;
g (xi-1) = mi-1 ,
g(xi) = fi .
(2)
Тогда, используя указанные выше условия, можно получить
следующую формулу для сплайна (1) /1, 2, 3/:
g(x)
m i 1 (x i x) 3
6h i
m i (x x i 1 ) 3
6h i
m i 1 h 2i x i x
m i h 2i x x i 1
fi 1
fi
6 hi
6 hi

7. Рассмотрим проведение сплайн-интерполяция не для функции g(x) по x, а для параметрического задания двух функций x(t) и y(t),

где t - параметр (время). В этом случае h = 1 и ti = i.
Тогда формула (3) значительно упрощается, поскольку в
этом
случае
xi=i;
xi-1=i-1
и
тогда
g(t )
m i 1 (i t ) 3
6
m i 1
m i (i 1 t ) 3
m
fi 1
i t f i i t i 1
6
6
6
Для того, чтобы вычислять конкретные значения по этой
формуле, необходимо знать коэффициенты m. Для их
определения возьмем производные на i и i+1 отрезках и
воспользуемся
условием
g (t+0) = g (t-0) .
(5)

8.

На i-том отрезке
g (t )
m i 1 (i t ) 2
2
m i 1
m i (t i 1) 2
m
fi 1
fi i
2
6
6
на i+1 - ом отрезке
mi
m i 1
m i (i 1 t ) 2 m i 1 (t i) 2
g (t )
fi 1
fi 1
2
2
6
6
Приравняем в соответствии с условием равенства производных
m i 1 i t m i t i 1
2
2
m i i 1 t
2
2
2
fi 1
m i 1 t i
2
2
m i 1
6
fi
mi
6
m i 1
mi
fi
fi 1
6
6

9.

Теперь учтем, что t = i. Тогда
m i 1 i i m i i i 1
2
2
m i i 1 i
2
2
2
fi 1
m i 1 i i
2
m i 1
6
fi
m i 1
mi
fi
fi 1
6
6
2
1
2
1
m i 1 m i m i 1 f i 1 2f i f i 1
6
3
6
m i 1 4m i m i 1 6 f i 1 2f i f i 1
mi
6

10.

Обозначим
6 f i 1 2f i f i 1 F i
и получаем следующую систему уравнений:
mo 4m1 m2 F1
m 4 m m F
2
3
2
1
.................................
m
4m
m F
n 1
n
n 1
n 2
m
n 1 4mn mn 1 Fn
i 1,..., N
(10)

11.

Система решается методом прогонки.
Прямым ходом прогонки находим
рекуррентных формулах
m
Для
n
L m
n
n 1
K
коэффициенты
в
n
m0:
m o L o m1 K o
Тогда для m1 из первой строки формулы (11) с учетом (13)
получаем:
L o m 1 K o 4m 1 m 2 F 1
F1 K o
1
m1
m2
4 Lo
4 Lo

12.

Отсюда
L1
1
4 Lo
K1
F1 K o
4 Lo
Или в общем виде
1
L
n
4 L
n 1
K
n
n 1
K
n
4 L
n 1
F
Задав условия Ko=Lo=0 последовательно находим все
коэффициенты K и L.
Далее выполняется обратный ход прогонки с учетом
естественных граничных условий: mo = mn=0.

13.

Кубический сплайн Акимы

14.

Сплайн Акимы – это особый вид сплайна,
устойчивый к выбросам. Для построения
сплайна Акимы требуется не менее 5 точек
Недостатком кубических сплайнов является
то, что они склонны осциллировать в
окрестностях точки, существенно отличающейся
от
своих
соседей
(http://web.snauka.ru/issues/2015/05/53846 ).

15.

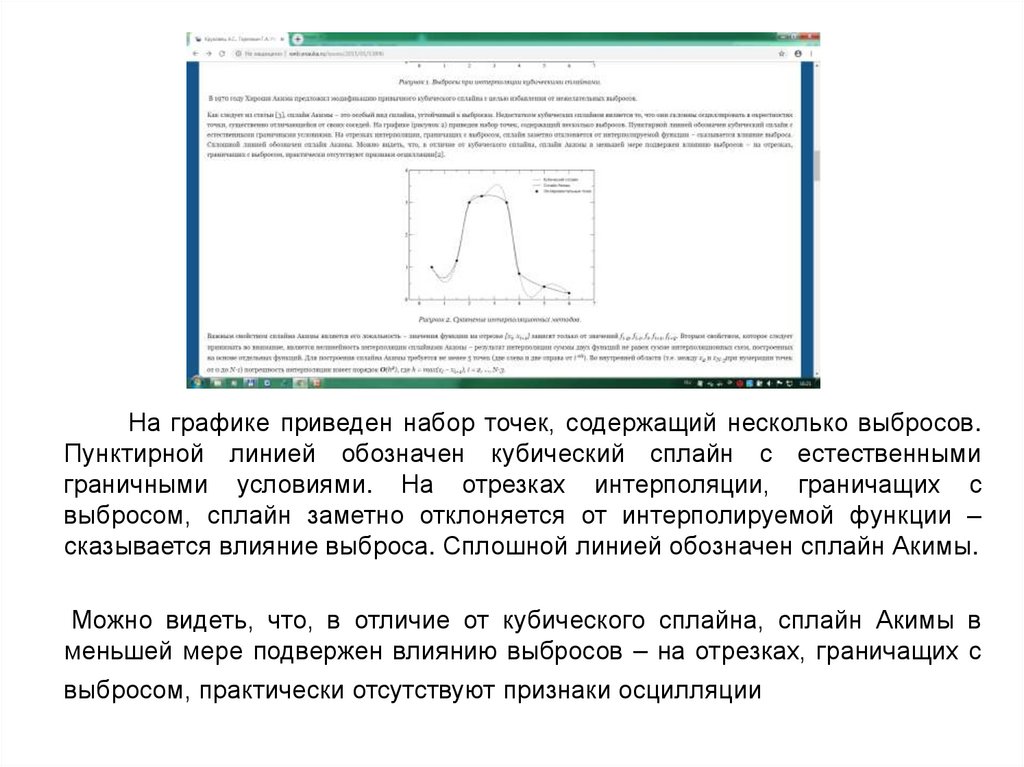
На графике приведен набор точек, содержащий несколько выбросов.
Пунктирной линией обозначен кубический сплайн с естественными
граничными условиями. На отрезках интерполяции, граничащих с
выбросом, сплайн заметно отклоняется от интерполируемой функции –
сказывается влияние выброса. Сплошной линией обозначен сплайн Акимы.
Можно видеть, что, в отличие от кубического сплайна, сплайн Акимы в
меньшей мере подвержен влиянию выбросов – на отрезках, граничащих с
выбросом, практически отсутствуют признаки осцилляции

16.

17.

18.

Список использованных источников
1. Шуп Т. Решение инженерных задач на ЭВМ.- М.: Мир, 1982.235 с.
2. Константинов А.Р., Химин Н.М. Применение сплайнов и метода
остаточных
отклонений
в
гидрометеорологии.Л.:
Гидрометеоиздат, 1983.- 184 с.
3. Корнейчук Н.П. Сплайны в теории приближения.- М.: Наука,
1984.-352 с.
4. Hiroshi Akima. A New Method of Interpolation and Smooth Curve
Fitting Based on Local Procedures, Изд.: ESSA Research
Laboratories, Institute for Telecommunication Sciences, Boulder
Journal of the ACM (JACM) Volume 17 Issue 4, 1970 стр. 589-602

19.

Программа «Сплайн»
Все аргументы: исходного вектора и аргументы для сплайнинтерполяции должны идти строго по убыванию!
Входные данные:
- номер колонки с аргументами x исходного вектора;
- номер колонки с соответствующими значениями функции y(x);
- общая длина исходного файла;
- номер колонки с аргументами для сплайна;
- количество аргументов для сплайна.
Выходные данные:
- колонка с данными сплайн-интерполяции (ее номер на 1 больше
номера колонки, содержащей аргументы для сплайна).

20.

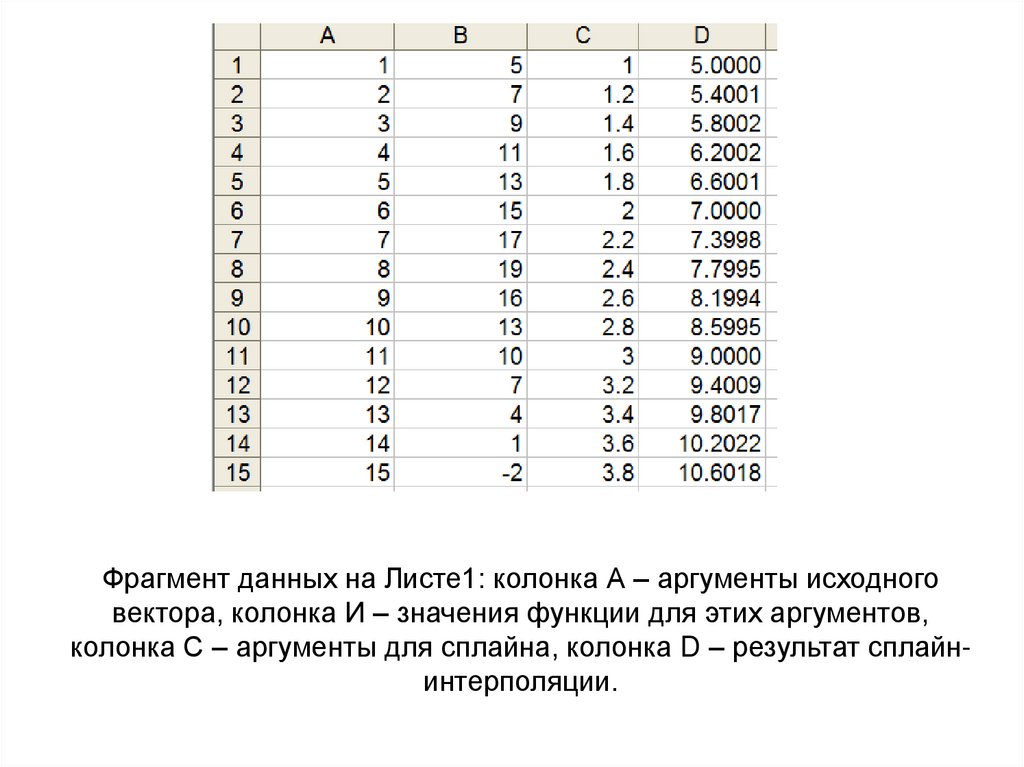
Фрагмент данных на Листе1: колонка А – аргументы исходного
вектора, колонка И – значения функции для этих аргументов,
колонка С – аргументы для сплайна, колонка D – результат сплайнинтерполяции.

21.

4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
35
30
25
20
15
10
5
0
-5
-10
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
-15
3
3
2
2
1
1
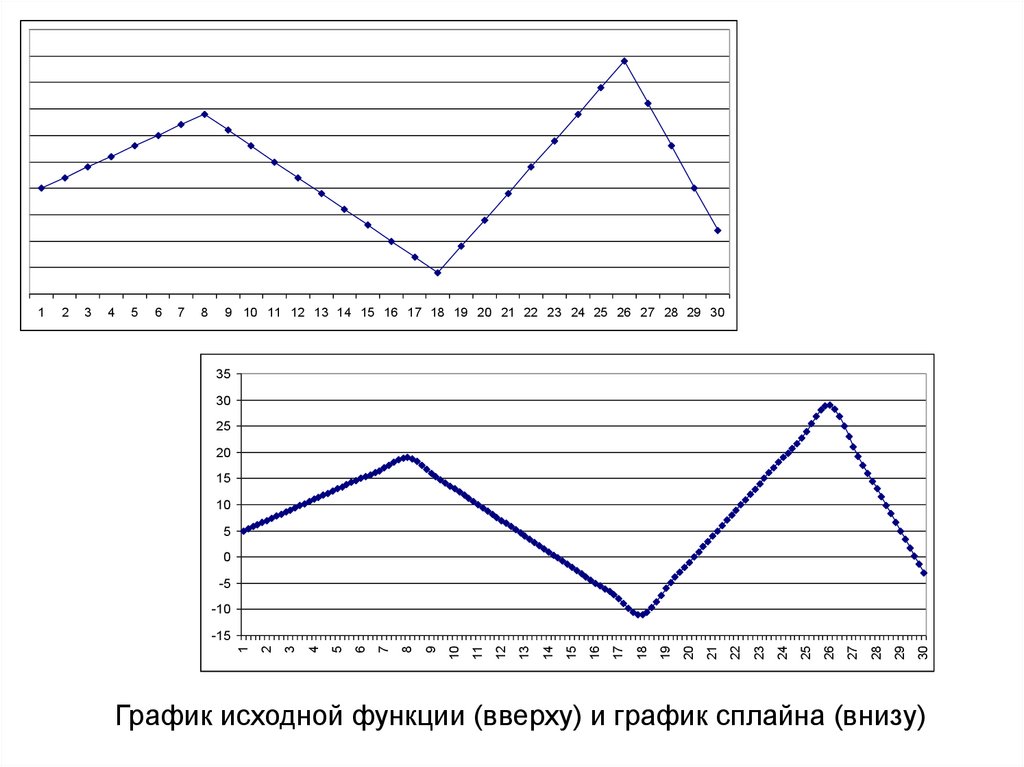
График исходной функции (вверху) и график сплайна (внизу)

22.

Какие будут вопросы?