Похожие презентации:
Численное моделирование стержневых систем (лекция 1)
1. Численное моделирование стержневых систем
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕСТЕРЖНЕВЫХ СИСТЕМ
1
2.
Основная литература1.
MIDAS Family Programs. http://www.midasit.ru.
2.
О. Зенкевич Метод конечных элементов в технике.
М.: Мир, 1976 – 542 с.
3.
Бате К., Вилсон Е. Численные методы анализа и
метод конечных элементов. – М., Стройиздат, 1982 – 448 с.
Дополнительная литература
4. Основы метода конечных элементов: учеб. пособие / Л.А.
Адегова, Б.М. Зиновьев. – Новосибирск: Изд-во СГУПСа, 2015.
– 131 с.
2
3.
Метод конечных элементов (МКЭ) — численный метод- решения дифференциальных уравнений с частными
производными,
- решения интегральных уравнений, возникающих при
решении
задач
прикладной
физики
(механики
деформируемого
твёрдого
тела,
теплообмена,
гидродинамики и электродинамики и т.д.).
История.
1954–1960 г.г. - Дж. Аргирис
- предложена матричная формулировка известных
численных методов для применения ЭВМ;
- Разработан общий метод расчета стержневых систем в
матричной форме на базе энергетических принципов,
- определена матрица податливости, введено понятие
матрицы жесткости (как обратной матрице податливости).
3
4.
1956 г. - Р. Клафф- опубликована первая работа, в которой была представлена
современная концепция МКЭ;
- на основе решения плоской задачи теории упругости
разработан треугольный конечный элемент, для которого
была описана матрица жесткости и вектор узловых сил.
- в 1960 г. впервые применен термин "конечный элемент"
("finite element") и этот год можно считать годом рождения
метода конечных элементов (МКЭ).
4
5.
1960–1965 г.г.- разработаны основные соотношения МКЭ на основе
вариационных принципов – метод стало возможным
использовать не только для решения задач строительной
механики, но и во многих других отраслях знаний
(гидродинамике, электротехнике и т.д.).
- на основе вариационных принципов созданы конечные
элементы для решения задач изгиба плит, тонких
оболочек, объемных твердых тел.
1967 г. - О. Зенкевич и И. Чанг
- опубликована первая монография о МКЭ, в которой
изложены основы метода и области его применения
1970-е г.г. - Р. Галлагер, Дж. Оден, Г. Стренг и другие
- математическая теория конечных элементов сформирована
в современном виде.
5
6.
Метод конечных элементов основан на- математическом представлении реальной сплошной
конструкции ее дискретной моделью (конечные элементы
объединяются между собой в узлах и только в узлах
можно достоверно говорить о состоянии конструкции);
- замене дифференциальных уравнений, описывающих
напряженно-деформированное состояние сплошных тел,
системой алгебраических уравнений.
Суть метода - область (одно- , двух- или трехмерная),
занимаемая конструкцией, разбивается на некоторое число
малых, но конечных по размерам подобластей, в которых
ищется решение системы (1.1).
Такие подобласти носят название конечных элементов (КЭ), а
сам процесс разбивки – дискретизацией или составлением
сетки КЭ.
6
7.
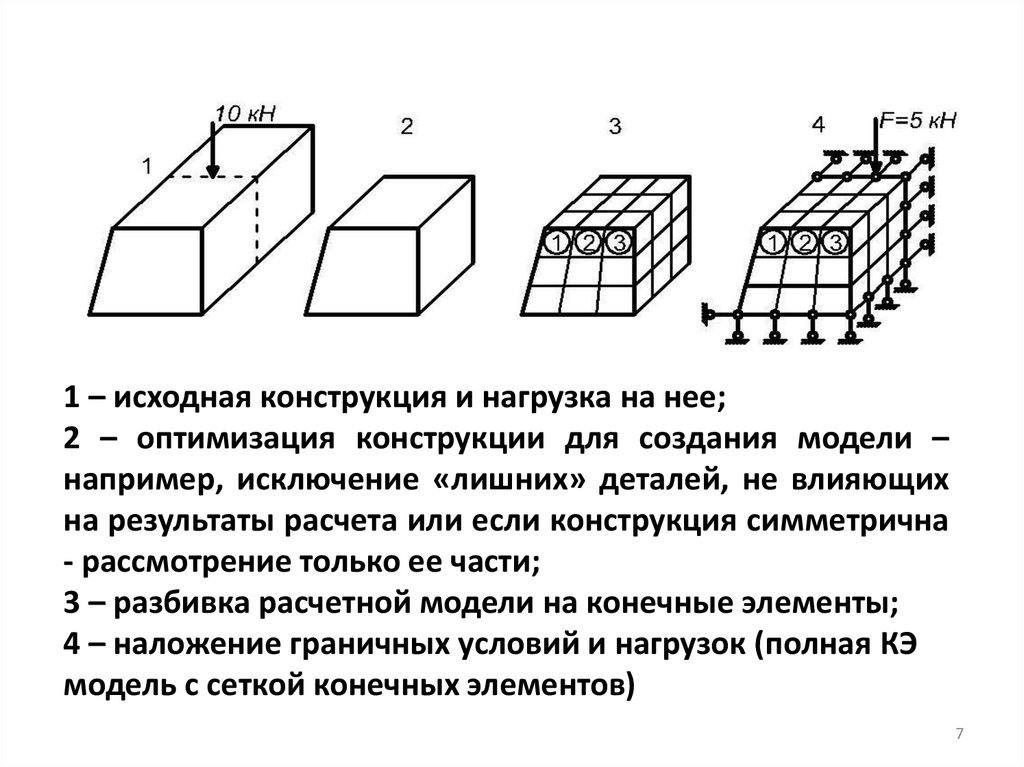
1 – исходная конструкция и нагрузка на нее;2 – оптимизация конструкции для создания модели –
например, исключение «лишних» деталей, не влияющих
на результаты расчета или если конструкция симметрична
- рассмотрение только ее части;
3 – разбивка расчетной модели на конечные элементы;
4 – наложение граничных условий и нагрузок (полная КЭ
модель с сеткой конечных элементов)
7
8.
В узлах- на
систему
накладываются
граничные
условия
(закрепления),
- прикладываются внешние силы,
- задаются свойства материала,
- ищется решение задачи в виде перемещений узлов и
реакций в узлах.
Для каждого узла составляются следующие векторы (здесь и
далее – терминология матричной алгебры):
- вектор-столбец перемещений узлов, вызванных внешними
усилиями
Т
u u
1
x
1
1
, u y , uz ,
n
n
n
, ux , u y , uz
- вектор-столбец внешних усилий и реакций в узлах
R Rx
1
1
1
n
n
n
, R y , Rz , , Rx , R y , Rz
Т
8
9.
Основное уравнение МКЭсвязывает эти два вектора
для
статических
расчетов
(1.1)
где {R} – вектор узловых сил, {u} – вектор узловых
перемещений, [K] – матрица жесткости системы (ансамбля)
конечных элементов.
Поскольку в КЭ-расчете известными (заданными) являются
внешние силы {R}, а неизвестными - перемещения узлов {u},
то уравнение (1.1) решается в виде
u K
1
R
(1.1а)
где [K ]-1 – матрица, обратная матрице жесткости [K].
9
10.
Уравнение (1.1) является частью полное уравнение движениядля статических и динамических расчетов
(1.2)
где [M] – матрица масс; [C ] – Матрица демпфирования; [K ] –
матрица жесткости; p(t) – нагрузка (реакции); u (t), ˙u (t) и ü(t)
– относительные перемещение, скорость и ускорение
соответственно
10
11.
Для перехода от узловых перемещений к перемещениям(напряжениям,
деформациям)
в
любой
точке
рассматриваемой области применяют интерполяционные
(аппроксимирующие) функции или функции формы.
В общем виде перемещения и координаты записываются как
n
U hi ui ;
i 1
n
X hi xi ,
i 1
(1.3)
где xi – координаты i-го узла элемента; ui – перемещения i-го
узла элемента; hi – интерполяционная функция (функция
формы ); n – число узлов.
В простейшем виде функции формы являются линейными.
11
12.
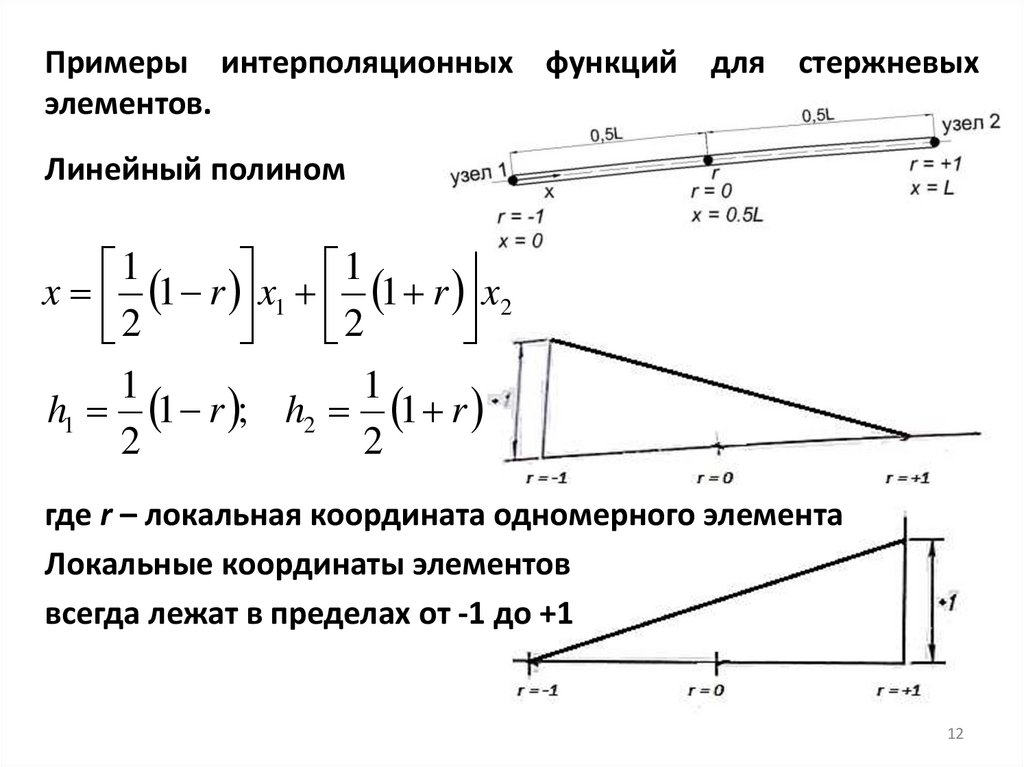
Примеры интерполяционных функций для стержневыхэлементов.
Линейный полином
1
1
x 1 r x1 1 r x2
2
2
1
1
h1 1 r ; h2 1 r
2
2
где r – локальная координата одномерного элемента
Локальные координаты элементов
всегда лежат в пределах от -1 до +1
12
13.
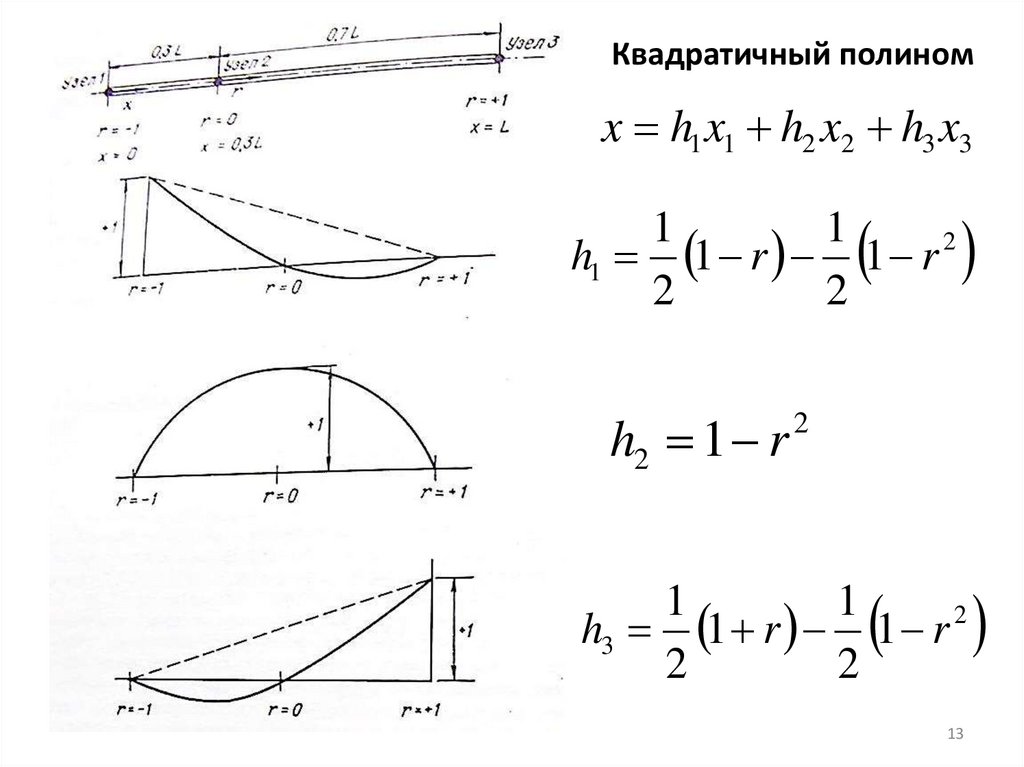
Квадратичный полиномx h1 x1 h2 x2 h3 x3
1
1
h1 1 r 1 r 2
2
2
h2 1 r
2
1
1
h3 1 r 1 r 2
2
2
13
14.
Кубический полином14
15.
Отсюда следует важное правило МКЭ– для повышения точности расчета в большинстве случаев
следует применять более частое расположение узлов, т.е.
создавать более мелкую разбивку модели на конечные
элементы.
Матрица жесткости конечного элемента в уравнениях (1.1) и
(1.2) содержит компоненты:
- отражающие деформативные свойства материала (матрицу
упругости [D]);
- отвечающие за интерполяцию данных между узлами
конечного элемента;
- выполняющие преобразование элементов матрицы,
записанных в локальной системе координат конечного
элемента, в глобальную систему координат всей модели.
15
16.
В общем виде элементы матрицы жесткости определяютсяпо формуле
K B D B dW
Т
,
(1.4)
W
где
[B] – матрица дифференциальных операторов, выполняющая
интерполяцию данных между узлами конечного элемента и
преобразование элементов матрицы из локальной системы
координат конечного элемента в глобальную систему
координат модели;
[D] – матрица упругости;
W – условное обозначение области интегрирования: для
стержневого элемента это будет его длина, для плоскостного
элемента – его площадь, для объемного элемента – его
объем.
16
17.
Поскольку в МКЭ интегрирование выполняется численно, торабочая формула для расчета элементов матрицы жесткости
имеет вид
n
m
l
К H r H s H t B D B det J
r 1 s 1 t 1
T
,
(1.5)
где r, s, t – количество точек интегрирования вдоль
соответствующих осей локальной системы координат
конечного элемента;
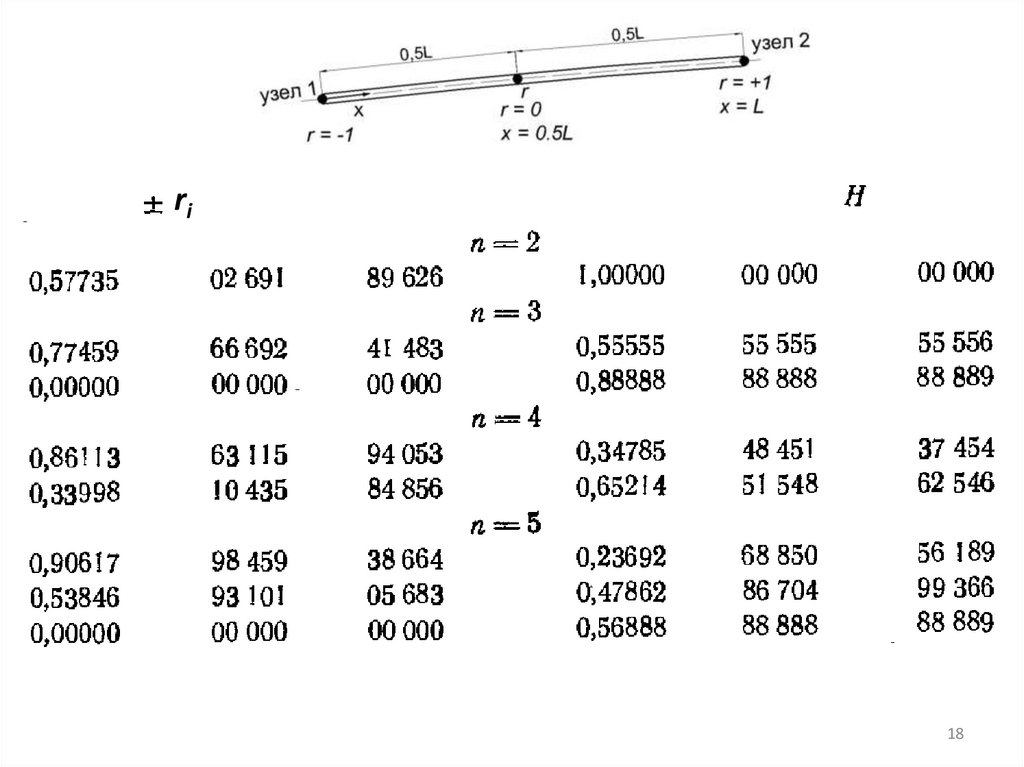
Hr, Hs, Ht – весовые коэффициенты квадратуры Гаусса
(принятого метода численного интегрирования);
det J – определитель матрицы Якоби.
17
18.
ri18
19.
Перемещения в узлах конечных элементов определяютсятакже соответствующими степенями свободы.
В балочных стержневых КЭ в общем случае существует шесть
степеней свободы
– три линейных перемещения вдоль соответствующих
локальных осей координат
- три угла поворота вокруг тех же осей.
Как разновидность стержневых элементов используются
ферменные стержни, названные так по характеру работы
элементов ферм – на продольные усилия.
В таких стержнях количество степеней свободы – две, только
линейные.
19
20.
Применение в одной модели конечных элементов с разнымколичеством степеней свободы может приводить к так
называемой сингулярности, когда модель становится
потенциально геометрически изменяемой.
В инженерной практике часто применяют сочетания в одной
модели конечных элементов с разным числом степеней
свободы в узлах:
- балочных (6 степеней свободы) и ферменных (2 степени
свободы),
- стержневых балочных КЭ (6 степеней свободы) и
плоскостных КЭ (3-5 степеней свободы),
- стержневых балочных КЭ (6 степеней свободы) и
объемных КЭ, у которых 3 степени свободы.
В этом случае к результатам расчетов следует относиться с
особым вниманием и осторожностью.
20
















 Строительство
Строительство








