Движение по окружности

1.

Движение
по окружности

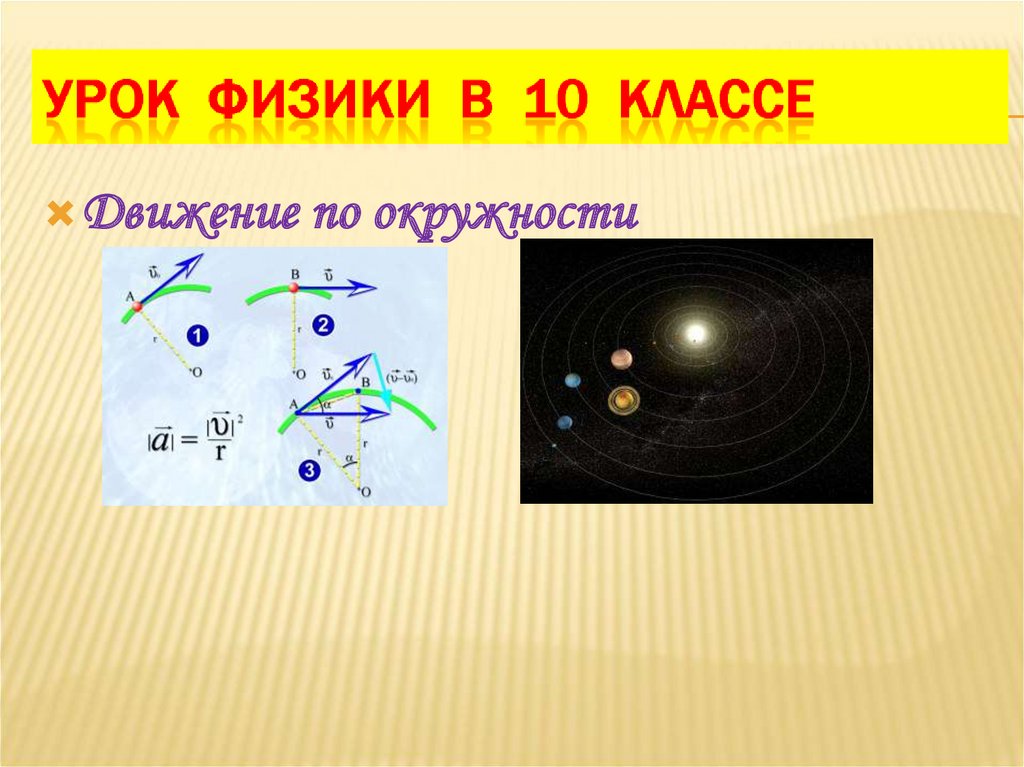
2. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ

– движение криволинейное, так как
траекторией является окружность.
– движение равномерное, так как модуль
скорости не меняется
V
– вектор скорости направлен по
касательной к окружности
– вектор ускорения направлен
а
а
к центру окружности
V
V

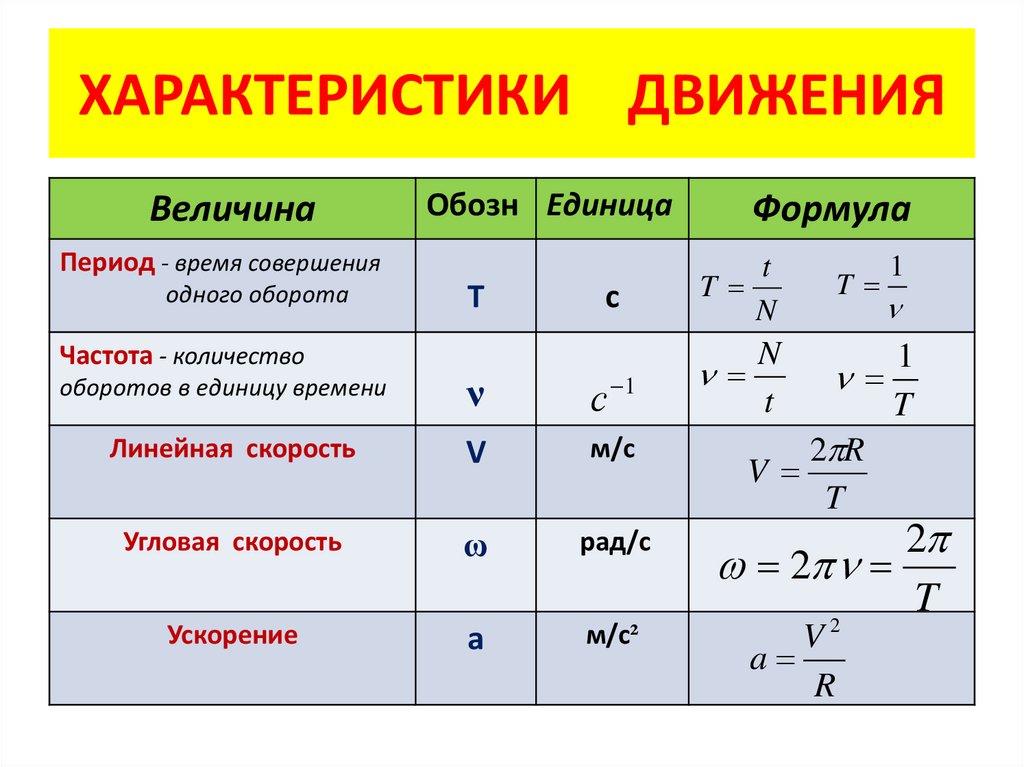
3. ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ

Величина
Обозн Единица
Период - время совершения
одного оборота
Частота - количество
Т
c
ν
с 1
Линейная скорость
V
м/с
Угловая скорость
ω
рад/с
Ускорение
a
м/с²
оборотов в единицу времени
Формула
t
T
N
T
1
N
t
1
T
2 R
V
T
2
2
T
V2
a
R

4. Шар, вращающийся на нити длиной 80см, совершил за одну минуту 150 оборотов. Определить все параметры вращательного движения

Дано:
СИ
Решение
t
T
R=80cм =0,8м
T = 60:150 = 0,4c
N
1
t = 1мин =60с
ν = 1:0,4 = 2,5с 1
T
N = 150
ω = 2πν
ω=2·3,14·2,5 = 15,7рад/с
2 R V =2·3,14·0,8:0,4=12,56м/с
v, T, a,ν,ω-?
V
Ответ:
T
V2
a
R
a = (12,56)²:0,8=197м/с²

5.

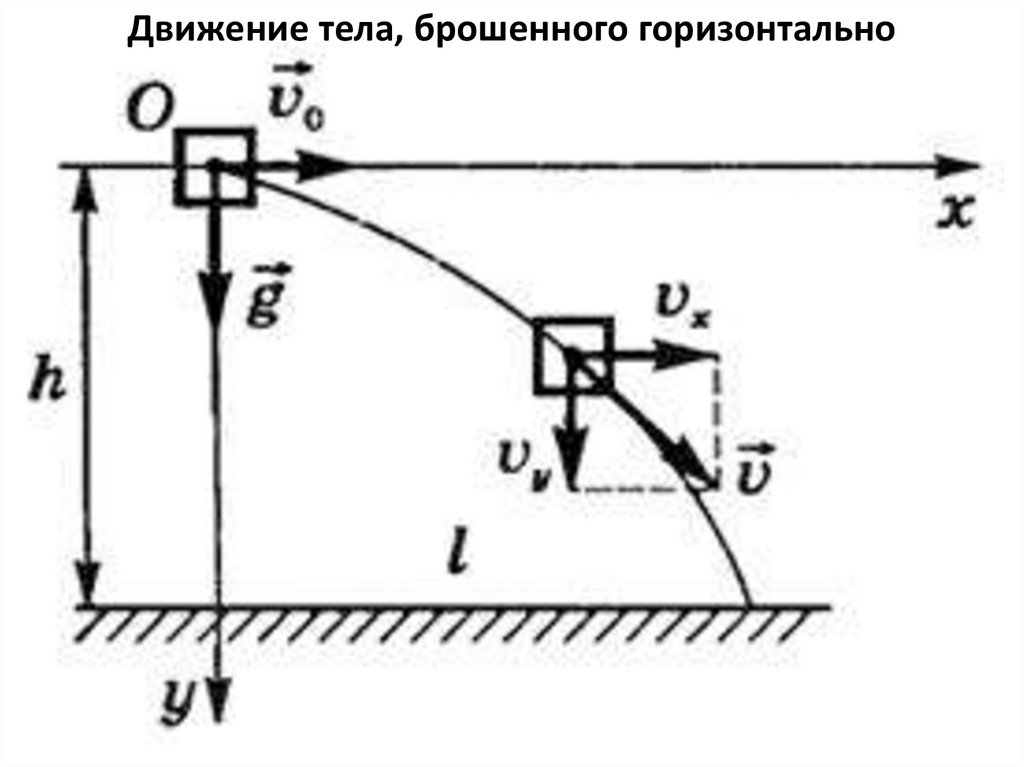
Движение тела, брошенного горизонтально

6.

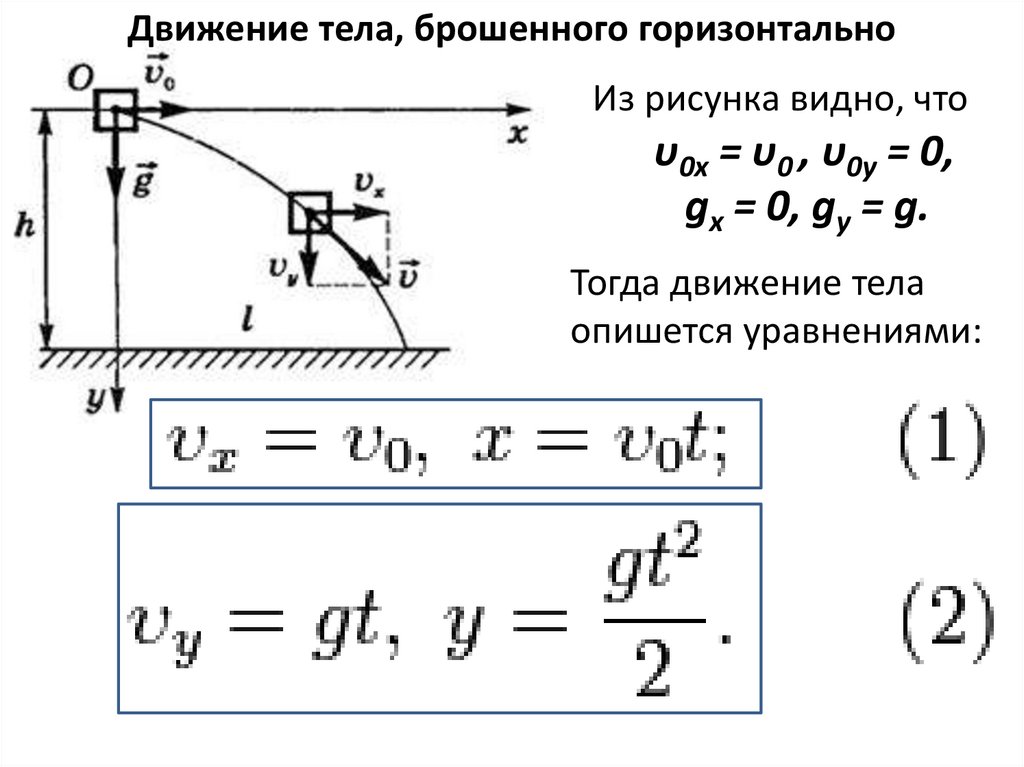
Движение тела, брошенного горизонтально
Из рисунка видно, что
υ0x = υ0 , υ0y = 0,
gx = 0, gy = g.
Тогда движение тела
опишется уравнениями:

7.

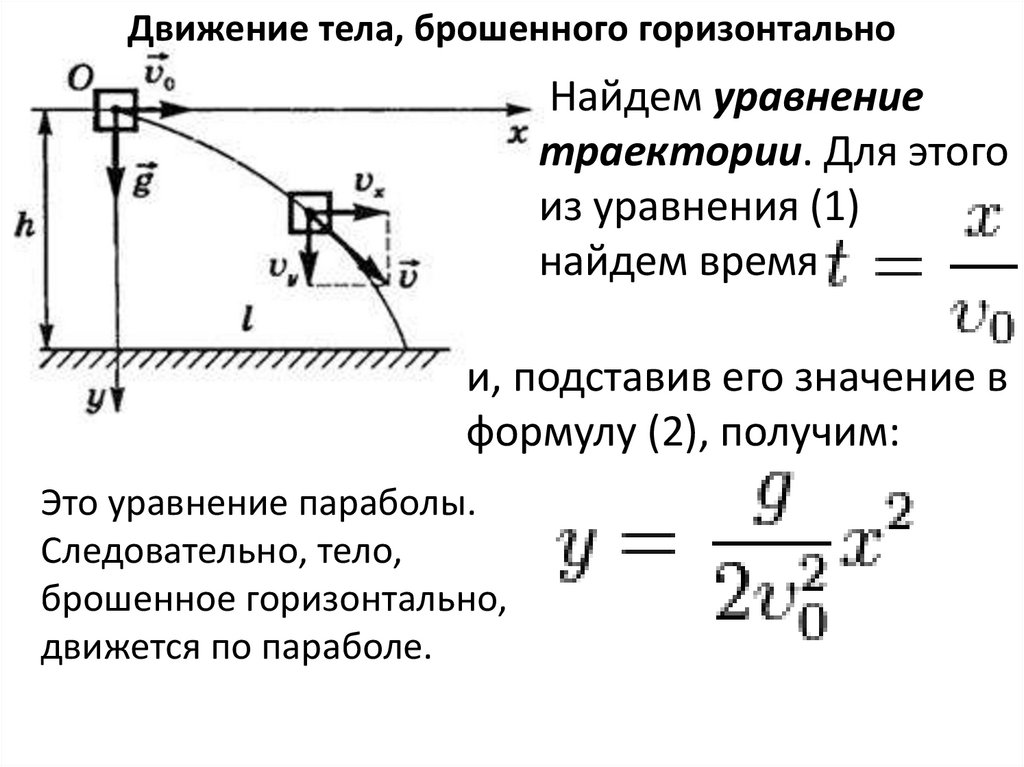
Движение тела, брошенного горизонтально
Найдем уравнение
траектории. Для этого
из уравнения (1)
найдем время
и, подставив его значение в
формулу (2), получим:
Это уравнение параболы.
Следовательно, тело,
брошенное горизонтально,
движется по параболе.

8.

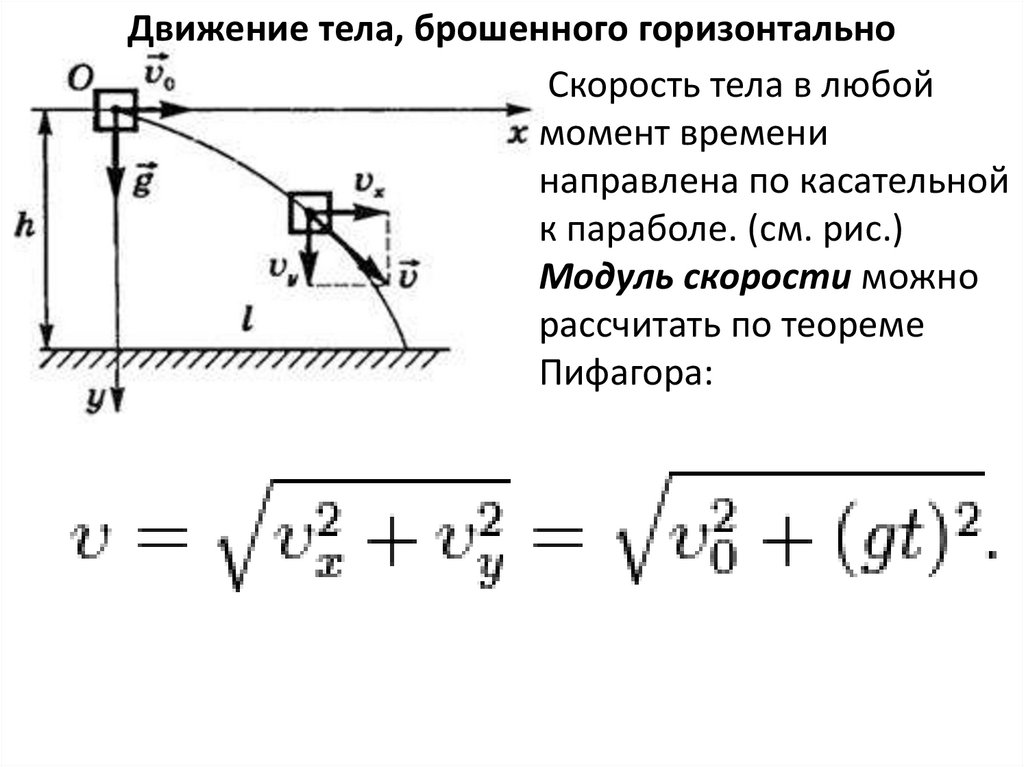
Движение тела, брошенного горизонтально
Скорость тела в любой
момент времени
направлена по касательной
к параболе. (см. рис.)
Модуль скорости можно
рассчитать по теореме
Пифагора:

9.

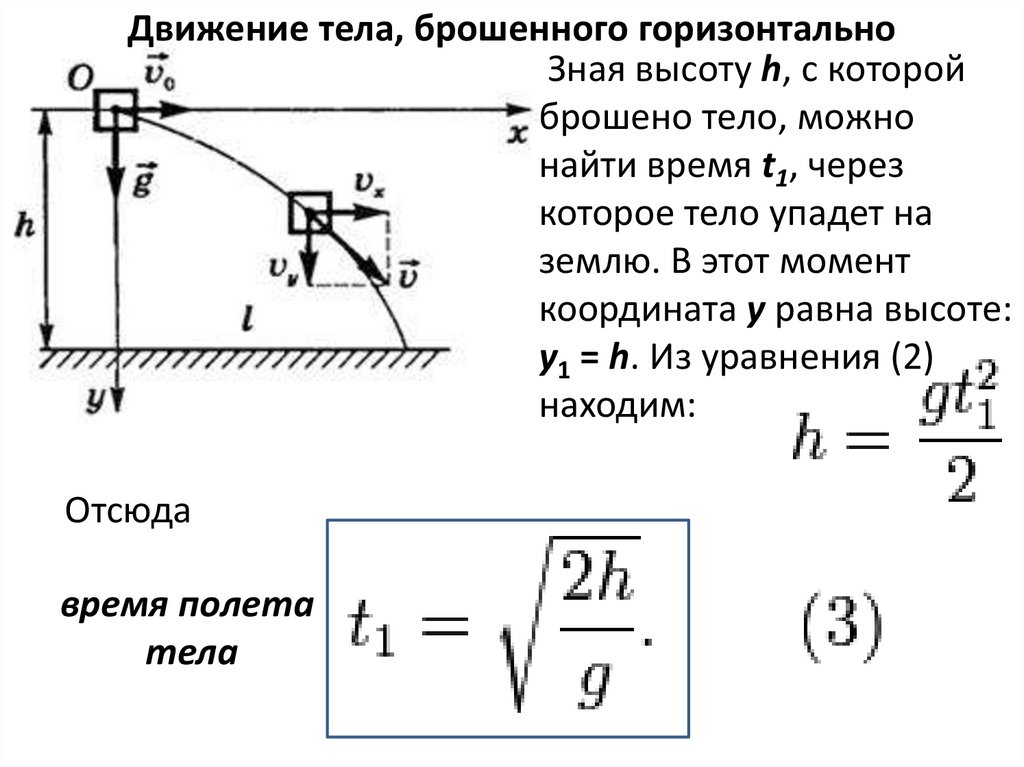
Движение тела, брошенного горизонтально
Зная высоту h, с которой
брошено тело, можно
найти время t1, через
которое тело упадет на
землю. В этот момент
координата y равна высоте:
y1 = h. Из уравнения (2)
находим:
Отсюда
время полета
тела

10.

.
Движение тела, брошенного горизонтально
Дальность полета можно
найти на основании
формулы (1),
учитывая, что l = x.
Следовательно,
дальность
полета
тела
Модуль скорости тела
в этот момент