Степенная функция

1.

2.

Определение степенной функции
.
Функция вида у = хр, где р – заданное
действительное число, а х –независимая
переменная, называется степенной функцией.
Свойства и график степенной функции зависят от
свойств степени с действительным показателем, и
в частности от того, при каких значениях х и р
имеет смысл степень хр.

3.

y
y=x4
y=x2
x

4.

— область определения — все
действительные числа, т.е. множество R;
— множество значений — неотрицательные
числа, т. е. у ≥ 0;
— функция у = х2n четная, так как
(-х)2n = х2n;
y
— функция является убываюy=x4
щей на промежутке х ≤ 0,
y=x
возрастающей
2
на промежутке х ≥ 0.
x

5.

у
0
х

6.

— область определения — все
действительные числа,
т.е. множество R;
— множество значений — все
действительные числа,
т.е. множество R;
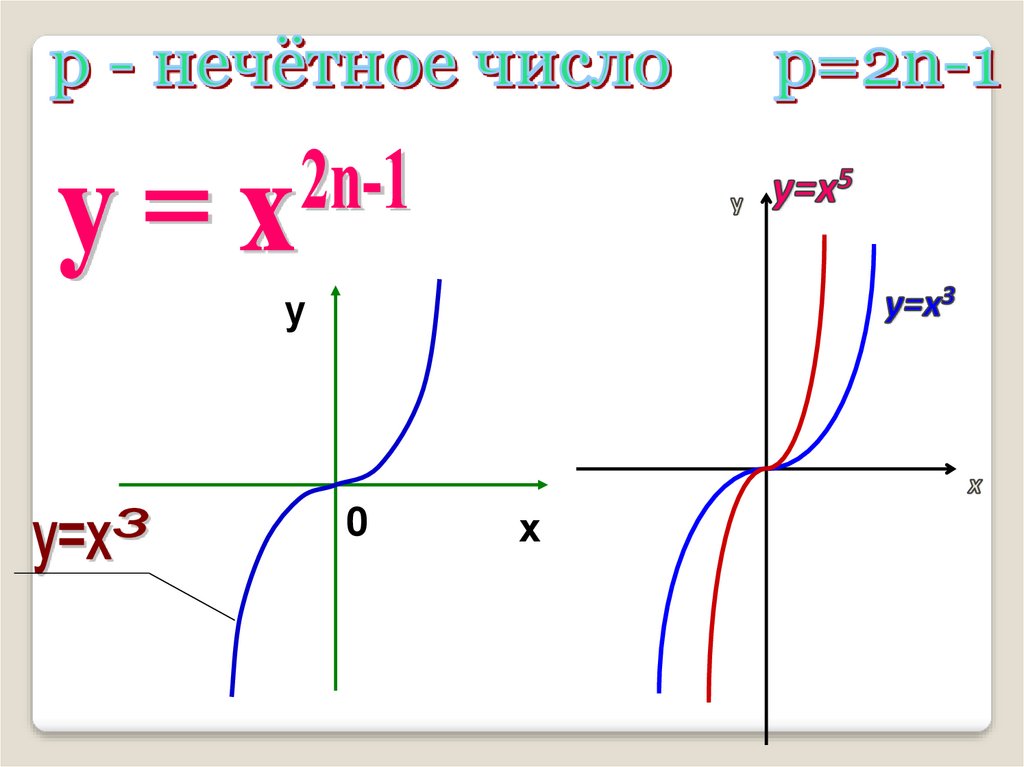
— функция у = х2n-1 нечетная,
так как (-х)2n-1 = -х2n-1;
— функция является
возрастающей
на промежутке х € R.
у
0
х

7.

0< p <1
y
y=x
1
0
1
1/3
График функции y
= xр, где p –
положительное
нецелое число,
имеет такой же
вид, как,
например, график
функции
y = x1/3
x (при 0< p <1).

8.

р – положительное действительное
нецелое число.
1. Область определения: Х
≥0
2. Множество значений: У ≥ 0
3. Нули функции при х=0
4. Функция является
возрастающей
на промежутке X
≥0
0< p <1

9.

p>1
y
Пример:
y=x
0
4/3
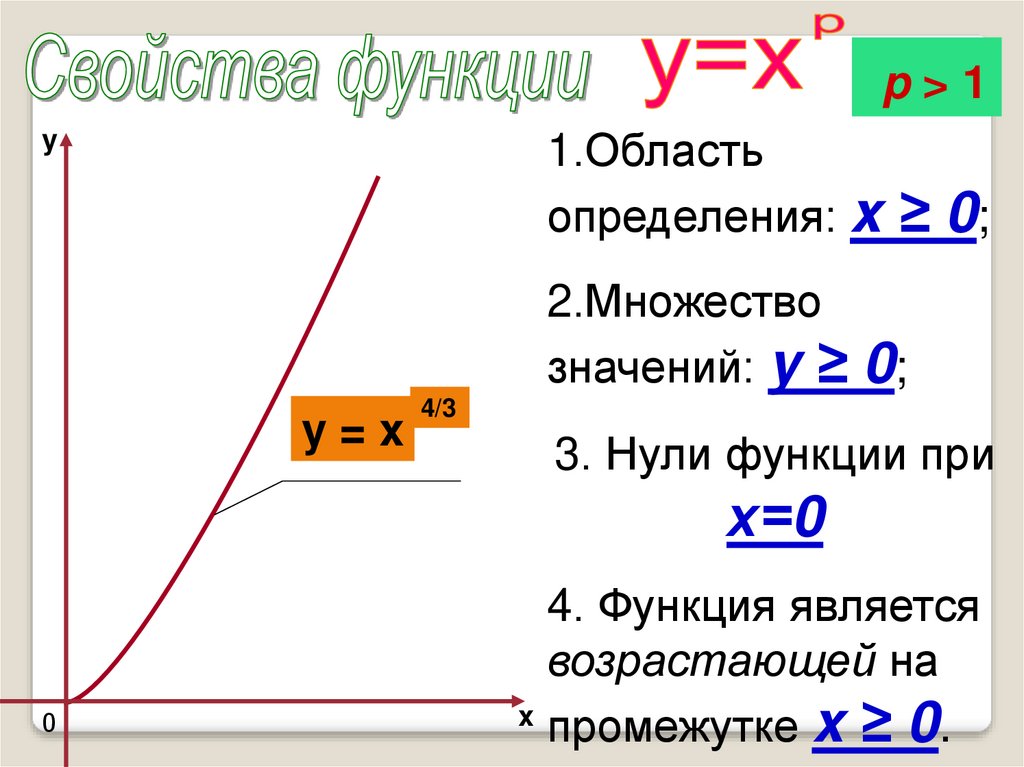
График функции
x
y = xр, где p –
положительное нецелое
число, имеет такой же
вид, как, например,
график функции y = x4/3
(при p >1).

10.

p>1
y
1.Область
определения: x
2.Множество
значений: y ≥
y=x
≥ 0;
0;
4/3
3. Нули функции при
х=0
0
4. Функция является
возрастающей на
x
промежутке x ≥ 0.

11.

p<0

12.

1. Область определения –
положительные числа
x>0;
2. Множество значений –
положительные числа
y>0;
3. Нулей нет
4. Функция является убывающей
на промежутке
x>0.
p<0