Похожие презентации:
Некоторые алгоритмы для массивов. Методы сортировки. Операции над матрицами
1.
Некоторые алгоритмы длямассивов.
Методы сортировки.
Операции над матрицами.
2.
Задача – проект 6_1. Вывести минимальный элементмассива X и его номер (индекс).
X
4
55
3
- 45
2
0
1
29
0
-5
min
-5
N_min
0
i
3.
X4
i= 3
55
- 45
2
0
1
29
0
-5
min
-5
N_min
0
4.
X4
i= 3
55
- 45
2
0
1
29
0
-5
min
- 45
N_min
3
5.
НачалоX
1
Задать массив X
2
4
55
3
- 45
2
0
1
29
0
-5
min
-5
N_min
0
min=X[0]
3
N_min=0
4
i
i=1, X.length-1, 1
нет
5
6
X[i] < min
да
min=X[i]
7
N_min=i
8
Вывести
min, N_min
Конец
6.
public class minElDemo{public static void minElArr (int X[ ]) {
int min = X[0], numMin = 0;
for (int i = 1; i < X.length; i++)
if (X[i] < min){
min = X[i];
numMin = i;
}
System.out.printf (
"Минимальный элемент массива: %d , его номер: %d\n",
min, numMin);
} //minElArr
7.
public static void putArr (int X[ ]) {for (int i = 0; i < X.length; i++)
System.out.printf("%d ", X[i]);
System.out.println();
} //putArr
public static void main (String args [ ]) {
int A [ ] = {-5, 29, 0, -45, 55};
System.out.println ("Массив A:");
putArr(A);
minElArr(A);
int В [ ] = {3, -7, 5, 9, -10, 7, -3};
System.out.println ("Массив B:");
putArr(В);
minElArr(В);
} //main
} //class
8.
Самостоятельно разработайте метод для нахождениямаксимального элемента массива и его номера.
9.
Изображение цикла forна схемах алгоритмов
ГОСТ 19.701-90 (ИСО 5807-85)
3.2.2.3. Блок «Подготовка»
Символ отображает
модификацию команды или
группы команд с целью
воздействия на некоторую
последующую функцию
(установка переключателя,
модификация индексного
регистра или инициализация
программы).
10.
ГОСТ 19.701-90 (ИСО 5807-85)Единая система программной документации
СХЕМЫ АЛГОРИТМОВ, ПРОГРАММ, ДАННЫХ И СИСТЕМ
Условные обозначения и правила выполнения
3.2.2.6. Блок
«Граница цикла»
Символ, состоящий
из двух частей,
отображает начало
и конец цикла. Обе
части символа
имеют один и тот же
идентификатор.
Условия для
инициализации,
приращения,
завершения и т.д.
помещаются внутри
символа в начале
или в конце в
зависимости от
расположения
операции,
проверяющей
условие.
11.
!?
!
12.
Методы сортировкиэлементов массива
13.
Дан массив {A[0], A[1], …, A[n-1]}.Переставить элементы массива так, чтобы
выполнялось условие:
A[0] ≤ A[1] ≤ A[2] ≤… ≤ A[n-1].
(*)
Идея метод алгоритм программа.
Пузырьковая сортировка
Идея: Анализируем соотношение (*) и замечаем,
что в паре соседних элементов левый не
больше правого.
Если в паре левый больше правого, их надо
переставить.
Метод пузырька основан на перестановке
соседних элементов!
14.
Пузырьковая сортировка (вариант1)15.
16.
17.
18.
19.
20.
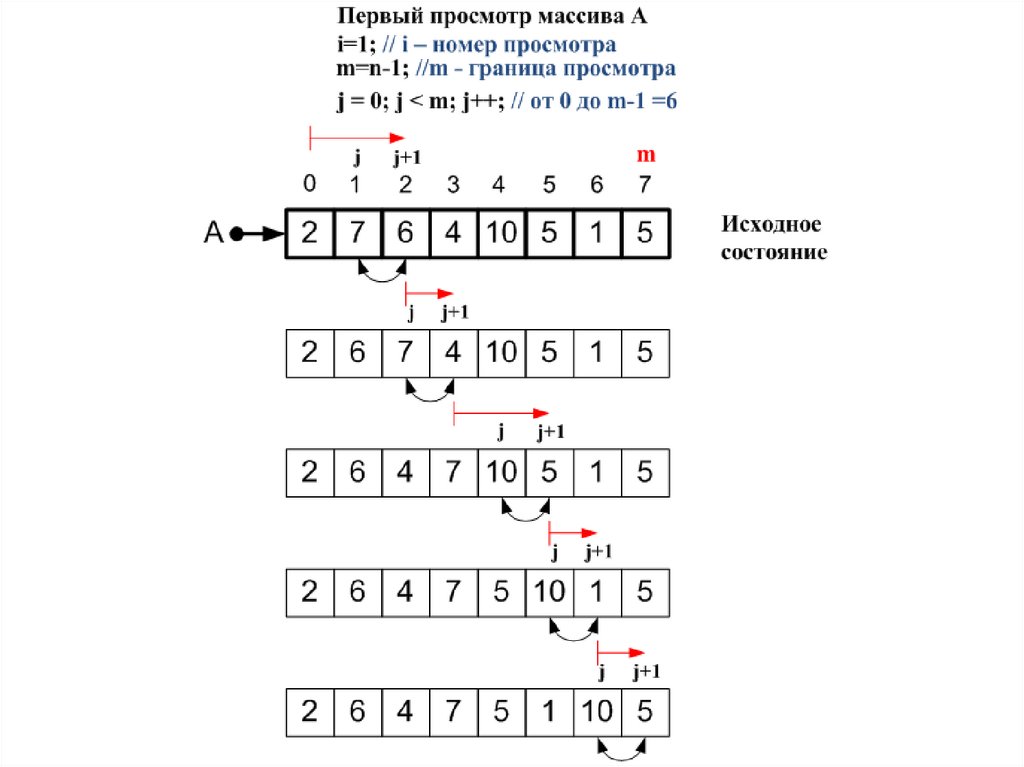
Результат первого просмотраСамый
большой
пузырек
всплыл!
21.
Итак, первый просмотр (i = 1) окончен,но не все элементы массива А
упорядочены.
Признак неупорядоченности массива:
при совершенном просмотре были
перестановки
22.
23.
24.
Результат второго просмотраСледующий
по величине
пузырек
всплыл!
25.
Итак, второй просмотр (i = 2) окончен,но не все элементы массива А
упорядочены.
Признак неупорядоченности – были
перестановки
26.
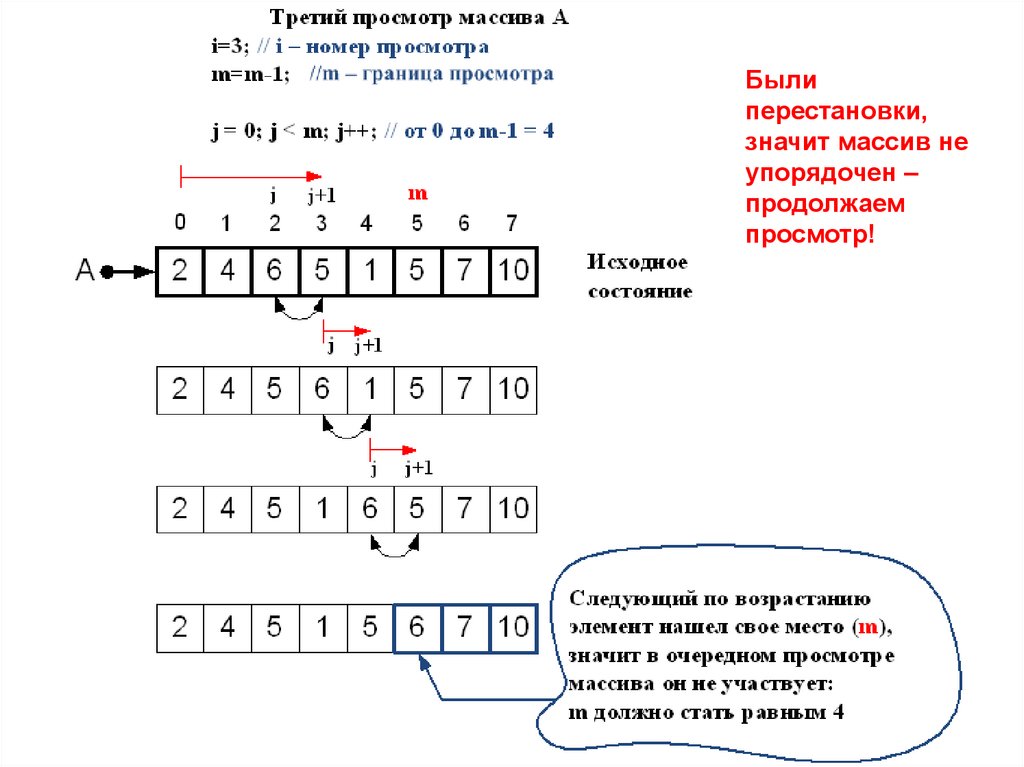
Былиперестановки,
значит массив не
упорядочен –
продолжаем
просмотр!
27.
Были перестановки, значит массив не упорядочен – продолжаемпросмотр!
28.
Были перестановки, значит массив не упорядочен – продолжаемпросмотр!
29.
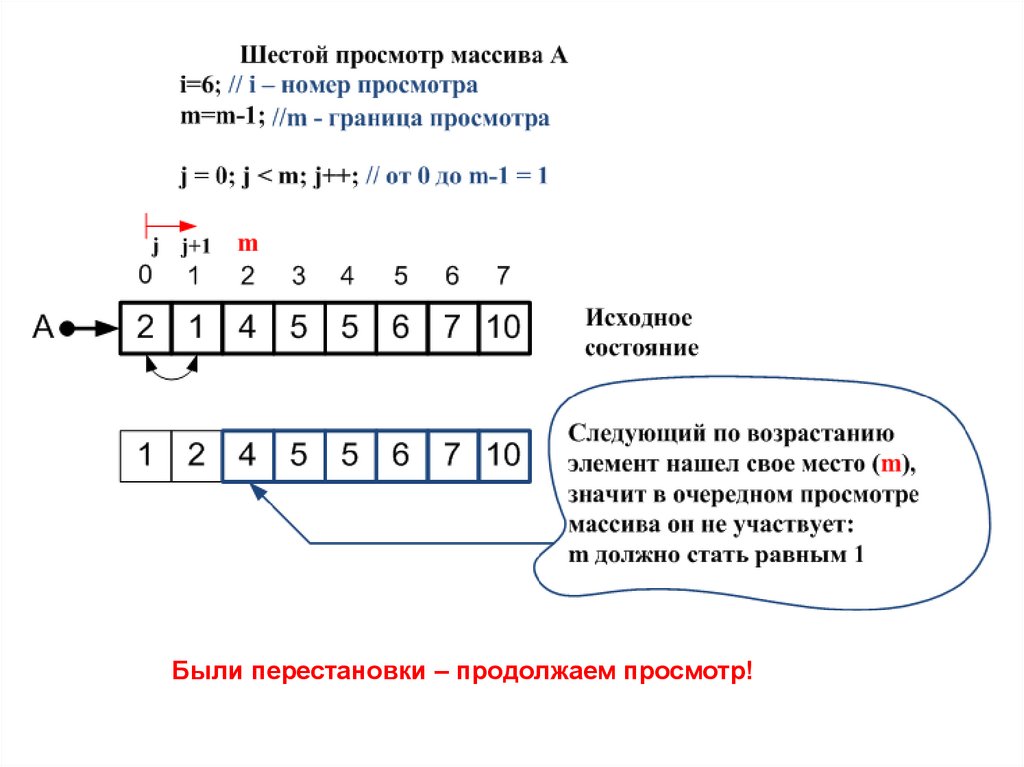
Были перестановки – продолжаем просмотр!30.
31.
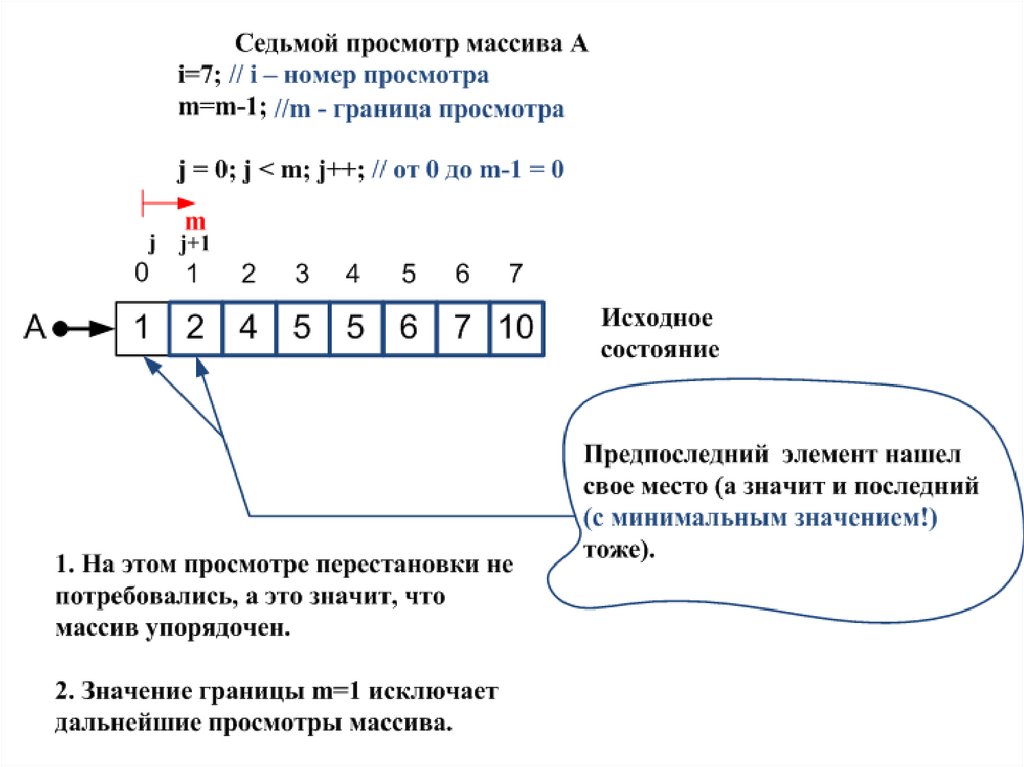
(почти упорядоченныймассив)
32.
Метод:Двигаясь от начала массива к концу, будем
в каждой паре соседних элементов
больший располагать справа.
Когда дойдем до конца массива, на
последнее место попадет максимальный.
Этот элемент уже не будет перемещаться.
Теперь повторяем процесс, но последний
элемент уже не рассматриваем и т.д.
Если при очередном просмотре массива
перестановок не было, значит массив
упорядочен и дальнейшие просмотры не
нужны.
33.
Схема алгоритмапроцедуры
упорядочивания
элементов
массива по
возрастанию
методом
пузырька
34.
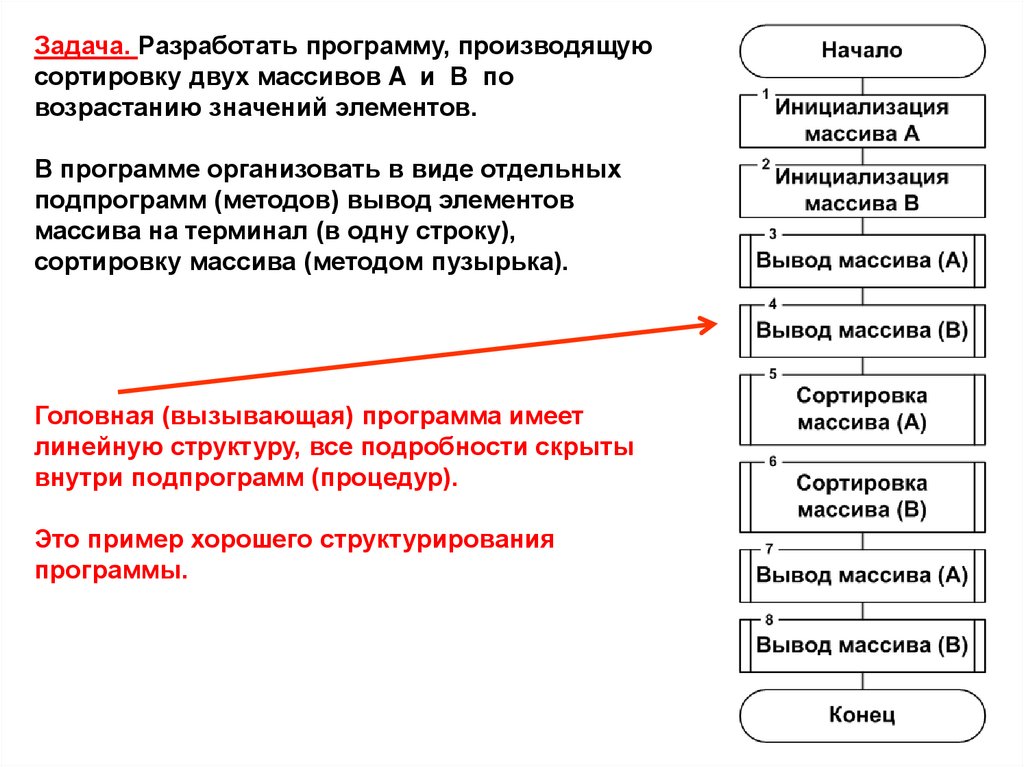
Задача. Разработать программу, производящуюсортировку двух массивов A и В по
возрастанию значений элементов.
В программе организовать в виде отдельных
подпрограмм (методов) вывод элементов
массива на терминал (в одну строку),
сортировку массива (методом пузырька).
Головная (вызывающая) программа имеет
линейную структуру, все подробности скрыты
внутри подпрограмм (процедур).
Это пример хорошего структурирования
программы.
35.
public class Сортировки{ //проект 6_2_1public static void пузырек (int [ ] A) {
boolean flag;
for (int m = A.length-1; m > 0; m--){
flag = true;
for (int j = 0; j < m; j++)
Продемонстрирована
возможность давать
if (A[ j ] > A[ j+1]) {
классам, методам (и
int b = A[ j ];
переменным) имена на
A[ j ] = A[ j+1];
кириллице.
A[ j+1] = b;
Но делать это
flag = false;
категорически не
рекомендется во избежание
}
синтаксических ошибок
if (flag) break;
(ряд букв на кириллице и
}
латинице пишется
одинаково).
} // пузырек
Лучше назвать метод
sortVial или boobleSort, а
класс – Sort.
36.
public static void putArr (int X[ ]) {for (int i = 0; i < X.length; i++)
System.out.printf("%d ", X[i]);
System.out.println();
} //putArr
public static void main (String[ ] args) {
int [ ] массив = {2,7,6,4,10,5,1,5}; // лучше int [ ] arr;
System.out.println ("До сортировки");
putArr (массив);
пузырек (массив);
System.out.println ("После сортировки");
putArr (массив);
System.out.println (); //--------------------------------------int [ ] arr = {2,3,5,4,6,7,8,9};
System.out.println ("До сортировки");
putArr (arr);
пузырек (arr);
System.out.println ("После сортировки");
putArr (arr);
} //main
} // class
37.
38.
Мини-тестНа перестановке каких элементов
основан метод пузырька?
Каково условие досрочного выхода
из цикла просмотров массива?
39.
Сортировка методом пузырька (вариант2)Метод: (вариант 2). С каждой парой связано
еще две пары:
с (A[i], A[i+1])
связаны (A[i-1], A[i] ) и (A[i+1], A[i+2] ) (кроме
первой и последней пар).
Поэтому, если в паре (A[i], A[i+1]) сделана
перестановка, на всякий случай надо начать
проверку с самого начала.
Если дошли до последней пары, а перестановки
не потребовались, значит массив отсортирован.
40.
Промоделируйтеалгоритм вручную на
рассмотренном выше
тестовом примере.
Изобразите алгоритм
двумя другими
(правильными)
способами.
41.
public class Sort { // проект 6_2_2public static void boobleSort2 (int [ ] A) {
boolean flag = false;
while( !flag ) { //Пока не отсортирован
flag = true; //Вот он оптимизм!
for (int j = 0; j < A.length-1; j++)
if (A[ j ] > A[ j+1]) {
int b = A[ j ];
A[ j ]=A[ j+1];
A[ j+1] = b;
flag = false; //Произошла перестановка
break; //Выходим из for сразу после перестановки,
//чтобы начать просмотр массива сначала
} //if
} //while
} // boobleSort 2
Задание: Промоделировать вручную работу метода
на приведенных выше примерах.
42.
public static void putArr (int X[ ]) {for (int i = 0; i < X.length; i++)
System.out.printf("%d ", X[i]);
System.out.println();
} //putArr
public static void main (String[ ] args){
int [ ] arr1 = {2, 7, 6, 4, 10, 5, 1, 5};
System.out.println ("До сортировки");
putArr (arr1);
boobleSort 2 (arr1);
System.out.println ("После сортировки");
putArr (arr1);
System.out.println (); //--------------------------------------int [ ] arr2 = {2,3,5,4,6,7,8,9};
System.out.println ("До сортировки");
putArr (arr2);
boobleSort 2 (arr2);
System.out.println ("После сортировки");
putArr (arr2);
На том же тестовом примере метод boobleSort2
} //main
даст те же результаты , что и пузырек (проверьте!)
} // class
43.
Тест – это совокупность входных и соответствующих им выходных данных, на которыхпроверяется правильность работы программы.
Набор тестов должен быть полным (чтобы проверить все ветви алгоритма), и, желательно, не
избыточным.
С чего начать разработку программы?
Анализируем, что должно быть на входе программы (входные данные) и что должно быть на
выходе программы (выходные данные).
Затем рисуем какой-либо пример (например, матрицу, которую нужно транспонировать, и
матрицу, полученную в результате транспонирования). Фактически, это один из тестовых
примеров, на котором будем проверять программу впоследствии. Анализируя этот пример,
пытаемся понять логику поставленной задачи (что и как должна делать программа).
Затем рисуем схему алгоритма (укрупненную, с обобщенными блоками – подпрограммами), т.е.
уже в самом начале предполагаем структурирование алгоритма.
Далее определяем входные и выходные данные для каждой их подпрограмм, строим алгоритмы
для подпрограмм (если подпрограммы очень простые, то можно обойтись и без рисования схемы
алгоритма) и набор тестов для каждой подпрограммы и для программы в целом. Набор тестов
должен быть полным (проверять все возможные ситуации), но не избыточным.
Кодируем программу на языке программирования.
Проверяем работу подпрограмм и программы на тестовых примерах. Проводим отладку (можно
пользоваться отладчиком BlueJ или вставлять «отладочные печати»).
В технологии объектного программирования есть свои особенности.
44.
Идея (2).Прямой выбор.
Минимальный из всех элементов должен иметь индекс
0. Минимальный среди оставшихся элементов должен
иметь индекс 1, и т.д. Это следует из соотношения
A[0] ≤ A[1] ≤ A[2] ≤… ≤ A[n-1] (*).
Метод.
Находим минимальный элемент в массиве и меняем
местами с А[0],
находим минимальный среди оставшихся и меняем
местами с A[1],
находим минимальный среди оставшихся и меняем
местами с A[2],
…,
находим минимальный из A[A.length-2] и A[A.length-1]
и меняем местами с A[A.length-2].
45.
Минимальный элементперемещен в начало,
сдвигаем границу
просмотра
46.
47.
Обоснование алгоритма. Пусть элементыA[0], A[1], …, A[i-1] - уже на своих местах.
Сейчас следует найти минимальный элемент
среди A[ i ], A[ i+1],…, A[ A.length-1 ]
и его номер, и поменять местами с элементом
A[ i]. Тогда на своих местах будут
A[0], A[1], …, A[i-1], A[i]. Количество правильно
расположенных элементов увеличилось на 1.
Следует это действие выполнить для i = 0, 1, …,
A.length – 2, и получится упорядоченный
массив.
48.
Схема алгоритмасортировки методом
прямого выбора
Массив
число элементов
АдресA,массива
(A) n
n = A.length
Начало
1
Для i
i:=0,n−2, 1
2
Внешний цикл
(изменение номера
начального элемента
последовательности −
границы просмотра)
min:=A[i];
3
N_min:=i
4
Нахождение
минимального
элемента
последовательности
и его номера
Для j
j:=i+1, n−1, 1
5
6
A[ j ]<min
да
min:=A[ j ];
7
N_min:=j
8
Для j
9
Перестановка
минимального и
начального элементов
последовательности
A[N_min]:=A[i];
10
A[i]:=min
11
Для i
Конец
нет
Внутренний цикл
(изменение номера
очередного
просматриваемого
элемента)
49.
public class Sort { // проект 6.2.3public static void sortDirectChoice (int [ ] A) {
//сортировка прямым выбором
int min, nMin; //переменные для минимума и
// номера мин. элемента
int i, j; //переменные циклов
for(i = 0; i < A.length-1; i++) {
//--поиск минимального элемента и его номера--min = A[ i ]; nMin = i;
for( j = i + 1; j < A.length; j++)
if(A[ j ] < min) {min = A[ j ]; nMin = j; }
//---минимум найден и записан в min----A[nMin] = A[ i ]; A[ i ] = min; //поменяли местами
} // for i
} // sortDirectChoice
50.
public static void putArr (int X[ ]) {for (int i = 0; i < X.length; i++)
System.out.printf("%d ", X[ i ]);
System.out.println();
} //putArr
public static void main (String[ ] args){
int [ ] arr1 = {2, 7, 6, 4, 10, 5, 1, 5};
System.out.println ("До сортировки");
putArr (arr1);
sortDirectChoice(arr1);
System.out.println ("После сортировки");
putArr (arr1);
System.out.println (); //--------------------------------------int [ ] arr2 = {2, 3, 5, 4, 6, 7, 8, 9};
System.out.println ("До сортировки");
putArr (arr2);
sortDirectChoice (arr2);
System.out.println ("После сортировки");
putArr (arr2);
} //main
} // class
51.
Идея (3).Прямые вставки
Предположим, что у нас есть упорядоченный
массив из i элементов:
A[0] ≤ A[1] ≤ A[2] ≤… ≤ A[i-1].
Если бы удалось добавить к этим элементам
еще один – Х , сохраняя
упорядоченность, длина (упорядоченного)
массива увеличилась бы на 1.
52.
Метод прямых вставок53.
Было:i=1
54.
Было:55.
Было:56.
Было:57.
Было:58.
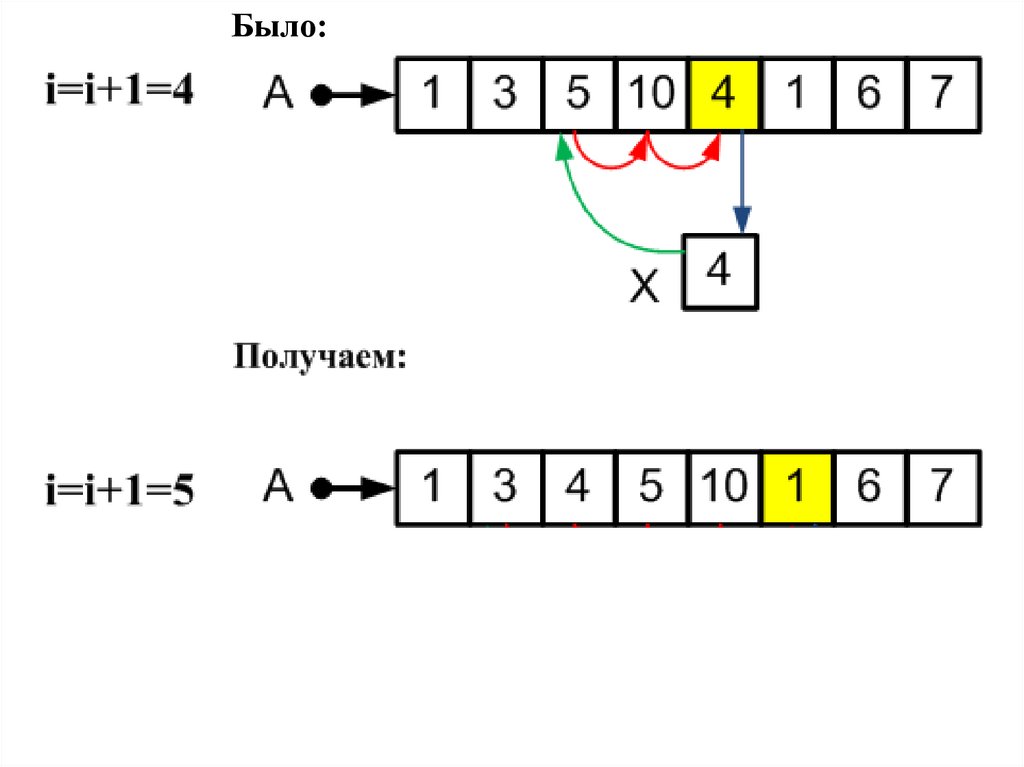
Начинаем с элемента сномером i= 1 (т.е. с А[1]).
1) Прячем его в карман X. А
2) Предыдущие элементы (в
данном случае A[0]), которые
больше Х, сдвигаем на одну
позицию вправо.
3) В освободившуюся позицию
вставляем Х.
0
1
2
3
4
5
6
7
10 3
5
1
4
1
6
7
3 10 5
1
4
1
6
7
5 10 1
4
1
6
7
1)
2)
3)
Метод
прямых
вставок (полностью)
Х 3
Получаем:
i=i+1=2
А
Х 5
Получаем:
i=i+1=3
А
3
Нужен вложенный
цикл со счетчиком j
j--
Х
1
Получаем:
i=i+1=4
А
1
3
5 10 4
1
6
7
5 10 1
6
7
5 10 6
7
Х
4
Получаем:
i=i+1=5
А
1
3
4
Х
Получаем:
А
i=i+1=6
и т. д. пока i < A.length
1
1
3
4
1
59.
Метод.Когда потребуется добавить к упорядоченному
массиву один элемент (Х), следует найти место для
этого элемента.
Место определяется соотношением:
A [слева] ≤ Х < A[справа].
Можно начать с упорядоченного "массива",
содержащего всего один элемент.
Поскольку после одного шага длина
упорядоченной части массива увеличивается,
повторяя шаги, можно упорядочить массив любой
длины.
При поиске места для Х движемся по массиву
влево, пока элемент массива больше Х. Как только
обнаружен элемент, не больший Х, справа от него
следует поместить Х.
Движение влево возможно, пока номер элемента
больше 0.
60.
Алгоритм. Добавляем к упорядоченному массивуэлемент A[ i ]. (Значение i должно изменяться от 1 до
A.length-1 с шагом 1).
Для этого "прячем" A[ i ] в «карман» Х, освобождая
место i.
Последовательно, начиная с элемента A[ j = i-1]
(условие: j≥0 ), сравниваем A[j] с Х.
Если Х<A[ j ], элемент А[ j ] перемещаем в позицию
[ j+1], уменьшаем j и повторяем проверку. Иначе (при
Х ≥ A[ j ] ) в позицию [ j+1] помещаем Х и проверки
заканчиваем.
Если дошли до элемента A[0] и место для Х не
найдено, его место – позиция 0.
61.
Схема алгоритмасортировки методом
прямых вставок
Адрес массива
(A)
Массив
A, число элементов
n
1
Копируем элемент А[i],
для которого ищем
место, в переменную x
Для i
i:=1,n−1, 1
x:=A[i];
3
5
Для j
j:=i-1, 0, 1
x<A[ j ]
да
A[ j+1]:=A[ j ];
6
Для j
Помещаем элемент из
переменной x на найденное
для него место
Внешний цикл
(изменение номера
элемента, для которого
ищем место, т.е. переход к
следующему элементу )
2
4
Передвигаем элемент A[ j ]
на одну позицию вправо
n = A.length
Начало
7
A[ j+1]:=x;
8
Для i
Конец
нет
break
Внутренний цикл
(передвижение вправо на
одну позицию элементов,
находящихся левее
элемента, для которого
ищем место, и значение
которых больше этого
элемента)
62.
public class Sort { // проект 6.2.4public static void sortDirectInsertion (int [ ] A) {
int x, i, j; // j должно быть «видно» в цикле for i
for (i = 1; i < A.length; i++) {
x = A[ i ];
for ( j = i - 1; j >= 0; j --)
if ( x < A[ j ] ) A [ j+1] = A[ j ];
else break;
A[ j+1] = x;
} //for i
} // sortDirectInsertion
63.
public static void putArr (int X[ ]) {for (int i = 0; i < X.length; i++)
System.out.printf("%d ", X[i]);
System.out.println();
} //putArr
public static void main (String[ ] args){
int [ ] arr1 = {2, 7, 6, 4, 10, 5, 1, 5};
System.out.println ("До сортировки");
putArr (arr1);
sortDirectInsertion(arr1);
System.out.println ("После сортировки");
putArr (arr1);
System.out.println (); //----------------------------int [ ] arr2 = {2, 3, 5, 4, 6, 7, 8, 9};
System.out.println ("До сортировки");
putArr (arr2);
sortDirectInsertion (arr2);
System.out.println ("После сортировки");
putArr (arr2);
} //main
} // class
Четыре
рассмотренных
метода
сортировки на
одних и тех же
тестовых
примерах дают
одинаковый
результат.
Проверьте!
64.
65.
Сумма первых n членов арифметической прогрессии:Sn = (2a1 + d(n - 1))n / 2,
где a1 – первый член прогрессии;
d – разность прогрессии.
Оценка трудоемкости алгоритма
Худший случай:
Для пузырьковой сортировки (вариант, рассмотренный
первым):
T=(n-1)*t + (n-2)*t + (n-3)*t +…+ 1*t
(n – число элементов массива, t –среднее время на
перестановку двух элементов массива)
a1 = t; d = t;
T = Sn = (2t + t(n - 1))n / 2 = 0.5t (n2 + n).
При больших n главная составляющая – n2.
Максимальное время выполнения простых методов
сортировки – порядка n2 t.
Более быстрый метод сортировки (рекурсивный) будет
рассмотрен позже.
66.
Алгоритмы обработкидвумерных массивов
(матриц)
67.
Задача – проект 6_3.Сформировать массив X, содержащий максимальные
элементы столбцов матрицы Y.
Y
X
0
1
2
3
0
3
72
-5
-4
1
8
6
-2
- 15
2
-3
- 24
9
- 55
3
-1
14
- 27
-1
4
95
36
0
- 11
95
72
9
-1
Y.length – число строк матрицы Y,
Y[0].length - число столбцов матрицы Y,
X.length=Y[0].length.
68.
Вспомнимпройденный
материал:
В Java
многомерный
массив – это
массив
массивов
!
!
69.
Начало1
Задать матрицу Y
2
j=0, Y[0].length-1, 1
Задача интересна тем, что
внешний цикл организован
по столбцам, а внутренний
по строкам.
3
max=Y [ 0, j ]
4
i=1, Y.length-1, 1
нет
5
6
Y [ i, j ] > max
да
max=Y [ i, j ]
7
X [ j ] = max
8
Вывести Y, X
Конец
На каждой итерации
внешнего цикла
фиксируется номер столбца.
Внутренний цикл
«пробегает» по всем
номерам строк, т.е.
перебираются все элементы
в зафиксированном столбце.
70.
public class MatrArrDemo{ // проект 6_3public static int[ ] MaxInColomn (int Y[ ][ ]){
int X [ ] = new int [ Y[0].length ]; // создает массив X,
//состоящий из Y[0].length элементов (слов памяти)
for (int j = 0; j < Y[0].length; j++) {
int max = Y[0][ j ];
for (int i = 1; i < Y.length; i++)
if (Y[ i ][ j ] > max) max = Y[ i ][ j ];
X[ j ] = max;
} //for j
return X; // метод возвращает адрес
// созданного одномерного массива
} //MaxInColomn
type arr_name [ ] = new type [n]; –
создание одномерного массива с
именем arr_name, состоящего из n
элементов (слов памяти) типа type.
Можно ли обойтись без
переменной max?
71.
public static void putMatr (int Y[ ][ ]){for (int i = 0; i < Y.length; i++) {
for (int j = 0; j < Y[0].length; j++)
System.out.printf ("% 5d",Y[ i ][ j ]);
System.out.println();
} //for i
} //putMatr
public static void putArr (int X[ ]){
for (int i = 0; i < X.length; i++)
System.out.printf ("% 5d", X[i]);
System.out.println();
} //putArr
72.
public static void main (String args [ ]){int Y [ ] [ ] = {
{3, 72, -5, -4},
{8, 6, -2, -15},
{-3, -24, 9, -55},
{-1, 14, -27, -1},
{95, 36, 0,-11}
};
int A [ ] [ ] = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};
System.out.println("Матрица Y:");
putMatr (Y);
int X[ ] = MaxInColomn(Y); //ссылочной переменной X присваивается адрес
// одномерного int-массива, возвращенный методом MaxInColomn ()
System.out.println("Массив Х для матрицы Y:");
putArr (X); // в метод putArr () передается значение ссылочной переменной X
System.out.println("Матрица A:");
putMatr (A);
System.out.println("Массив Х для матрицы A:");
putArr (MaxInColomn(A)); // в метод putArr () передается адрес
// одномерного int-массива, возвращенный методом MaxInColomn ()
} //main
} //class
73.
74.
Перемножение матрицЕсли надо перемножить квадратные матрицы, то они должны
иметь одинаковую размерность.
75.
76.
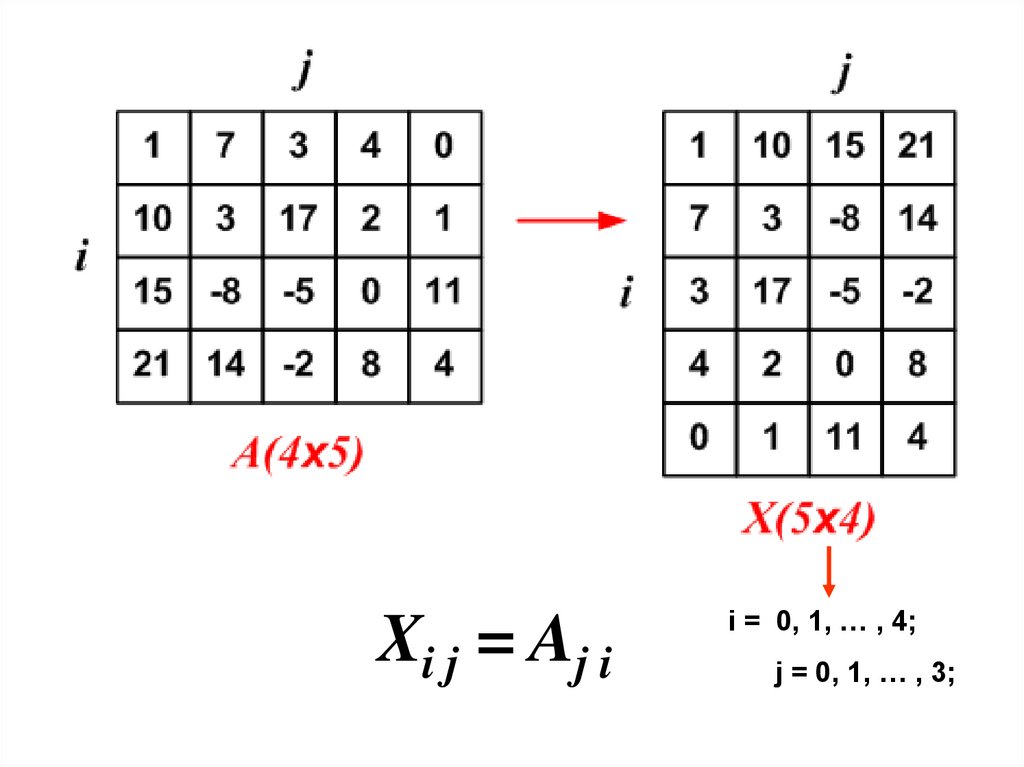
Транспонирование матрицы(строки становятся столбцами и наоборот)
j
i
j
1
7
3
4
0
1
10 15 21
6
10
3
17
2
1
7
3
-8
14
5
15
-8
-5
0
11
3
17
-5
-2
4
21 14
-2
8
4
4
2
0
8
-3
6
4
-3
-1
0
1
11
4
-1
5
i
A(5x5)
X(5x5)
Xi j = A j i
i = 0, 1, … , 4;
j = 0, 1, … , 4;
77.
Xi j = Aj ii = 0, 1, … , 4;
j = 0, 1, … , 3;
78.
public class MatrDemo1{public static int [ ][ ] multiplyMatr (int A[ ][ ], int B[ ][ ]) {
// перемножение матриц
if (A[0].length != B.length) return null; //выход и
// возврат null
int [ ][ ] C = new int [A.length] [B[0].length];
for (int i = 0; i < A.length; i++)
for (int j = 0; j < B[0].length; j++) {
C[ i ][ j ] = 0;
for (int k = 0; k < B.length; k++)
C[ i ][ j ] = C[ i ][ j ] + A[ i ][ k ] * B[ k ][ j ];
}
return C; //выход и возврат ссылки на матрицу С
}
79.
public static int [ ][ ] transpMatr (int A[ ][ ]){// транспонирование матрицы
int [ ][ ] X = new int [A[0].length][A.length];
for (int i = 0; i < A[0].length; i++)
for (int j = 0; j < A.length; j++)
X[ i ][ j ] = A[ j ][ i ];
return X;
}
80.
public static void putMatr (int Y[ ][ ]){Метод multiplyMatr () может
if (Y == null){
вернуть null-ссылку.
System.out.println("null");
Предусмотрим это в методе
return;
putMatr ().
}
for (int i = 0; i < Y.length; i++) {
for (int j = 0; j < Y[0].length; j++)
System.out.printf ("% 5d",Y[ i ][ j ]);
System.out.println();
} //for i
} //putMatr
public static void main (String args [ ]){
int Y1 [ ] [ ] = {
{1, 3, 2,},
{6, 4, 5,}
};
int Y2 [ ] [ ] = {
{3, 2, 1},
{2, 1, 3},
{4, 3, 0}
};
81.
System.out.println("Матрица Y1:");putMatr (Y1);
System.out.println("Матрица Y2:");
putMatr (Y2);
System.out.println("Результат транспонирования Y1 :");
putMatr (transpMatr(Y1));
System.out.println("Результат умножения Y1 и Y2:");
putMatr (multiplyMatr (Y1,Y2));
System.out.println("Результат умножения Y2 на Y1:"); //null
putMatr (multiplyMatr (Y2,Y1));
Y1 = multiplyMatr (Y1,Y2); // переменной Y1 присвоена ссылка на
//двумерный массив, которую вернул
//метод multiplyMatr
System.out.println("Y1=Y1*Y2:");
putMatr (Y1);
Y2 = transpMatr (Y1);
// переменной Y2 присвоена ссылка на
//двумерный массив, которую вернул
//метод transpMatr
System.out.println("Y2 = transp(Y1):");
putMatr(Y2);
System.out.println("Результат умножения Y2 на Y1:");
putMatr(multiplyMatr (Y2,Y1));
} //main
} //class











































































 Программирование
Программирование








