Предмет начертательной геометрии

1. Предмет начертательной геометрии

Начертательная геометрия является одной из
фундаментальных наук, составляющих основу инженернотехнического образования. Она изучает методы
изображений пространственных геометрических фигур на
плоскости и способы решения по этим изображениям
метрических и позиционных задач в пространстве.
Методы начертательной геометрии позволяют
решать многие прикладные задачи специальных
инженерных
дисциплин
(механики,
химии,
кристаллографии, картографии, инструментоведения и
др.)
Начертательная геометрия развивает у человека
пространственное мышление, без которого немыслимо
никакое инженерное творчество.

2. Из истории начертательной геометрии

Начертательная геометрия как наука была создана в конце XVIII века великим
французским геометром и инженером Гаспаром Монжем (1746 – 1818).
Первые идеи об ортогональном проецировании пространственных фигур на
плоскость высказывались еще задолго до Монжа в XVI веке немецким
математиком и художником Альбрехтом Дюрером (1471 –1528), который
разработал метод ортогонального изображения конических сечений и некоторых
пространственных кривых.
В 1637 г. французский геометр и философ Рене Декарт (1596 – 1650) создал
метод координат и заложил основы аналитической геометрии, а его
соотечественник, инженер и математик Жирар Дезаг (1593 – 1662), использовал
этот метод координат для построения перспективных проекций и обосновал
теорию аксонометрических проекций.
В XVII веке в России успешно развивались технические чертежи, выполненные в
виде планов и профилей в масштабе. Здесь в первую очередь следует назвать
чертежи выдающегося русского механика и изобретателя И. П. Кулибина (1735 –
1818).

3. Способы проецирования

В начертательной геометрии пространственные формы
предметов действительного мира и соответствующие геометрические
закономерности изучаются при помощи изображений на плоскости –
чертежей.
Чертеж при этом является инструментом, с помощью которого
осуществляется непосредственное изучение геометрических форм
предметов и выполняется решение пространственных задач. Не всякое
изображение предмета на листе бумаги позволяет точно определить его
геометрическую фигуру.
Для того, чтобы чертеж был геометрически равноценным
изображаемому предмету (а только в этом случае можно изучать сам
предмет по его чертежу), он должен быть построен при помощи метода
проецирования (от латинского слова ргоjесеге – бросать вперед).

4. Способы проецирования

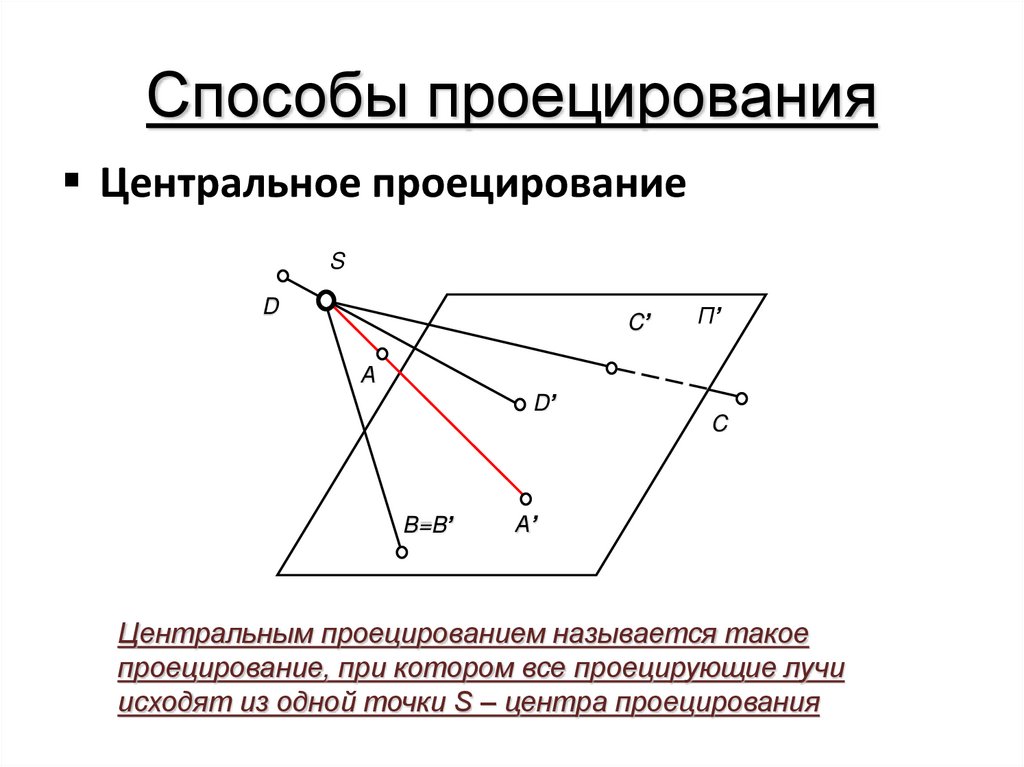
Центральное проецирование
S
D
C’
П’
А
D’
B=B’
C
А’
Центральным проецированием называется такое
проецирование, при котором все проецирующие лучи
исходят из одной точки S – центра проецирования

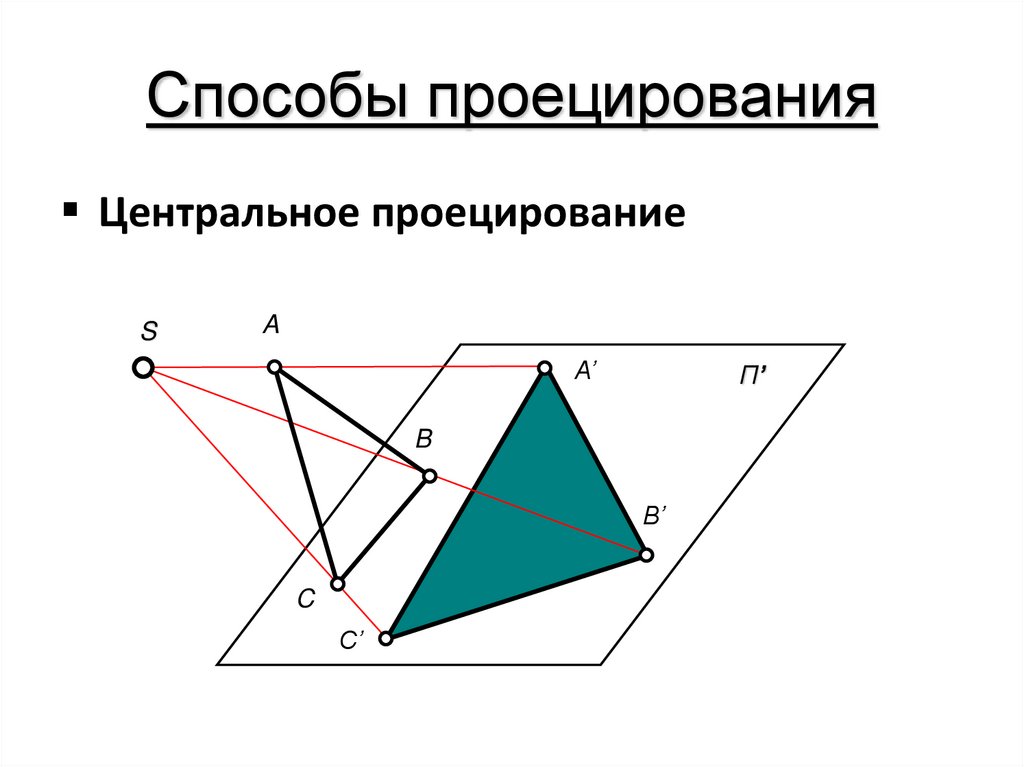
5. Способы проецирования

Центральное проецирование
S
A
A’
П’
B
B’
C
C’

6. Способы проецирования

Центральное проецирование
Свойства центральной проекции:
1. проекцией точки является точка
2. проекцией прямой линии является
прямая линия
3. проекцией точки, лежащей на
некоторой прямой, является точка,
лежащая на проекции данной прямой

7. Способы проецирования

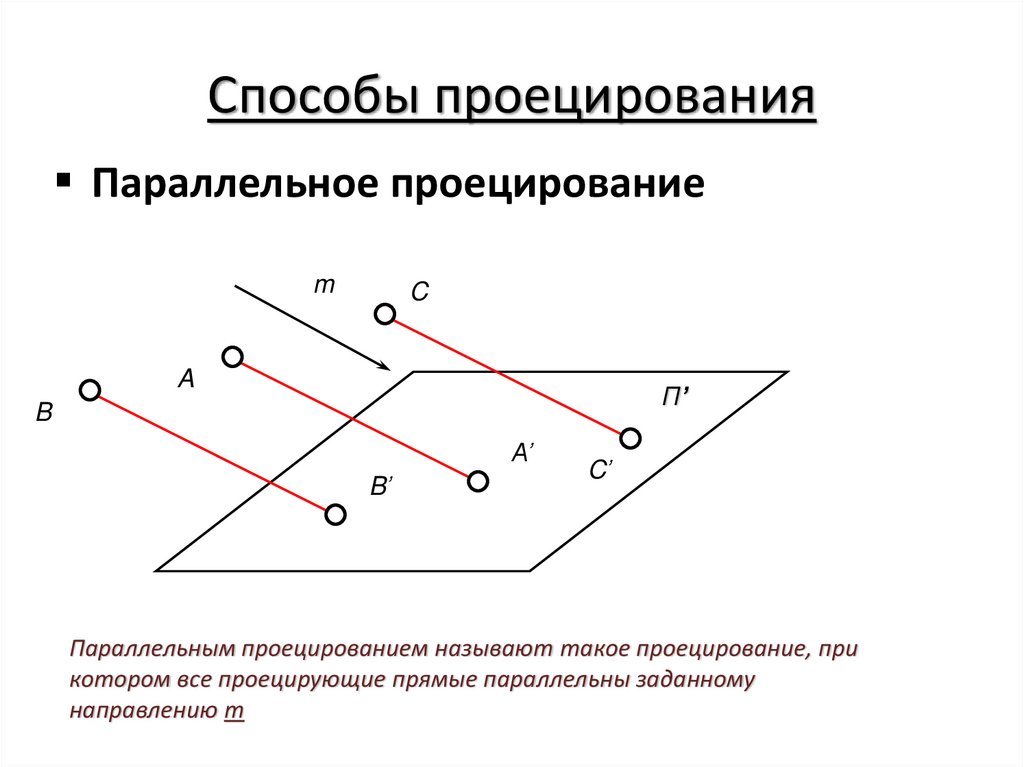
Параллельное проецирование
m
C
A
П’
B
A’
B’
C’
Параллельным проецированием называют такое проецирование, при
котором все проецирующие прямые параллельны заданному
направлению m

8.

Способы проецирования
Параллельное проецирование
Параллельная проекция кроме трех свойств
центральной проекции обладает еще
дополнительными свойствами:
4. проекциями параллельных прямых являются параллельные
прямые
5. отношение проекций отрезков, лежащих на параллельных
прямых или на одной и той же прямой, равно отношению
самих отрезков
6. проекция фигуры не меняется при параллельном переносе
плоскости проекций

9. Ортогональное проецирование

Способы проецирования
Ортогональное проецирование
Ортогональное проецирование является частным
случаем параллельного проецирования.
Направление проецирования «m» перпендикулярно
(ортогонально) плоскости проекций .
Ортогональному проецированию присущи все свойства
параллельного и центрального проецирования и кроме того,
справедлива теорема о проецировании прямого угла: если
хотя бы одна сторона прямого угла параллельна плоскости
проекций, а вторая не перпендикулярна ей, то прямой угол
на эту плоскость проецируется в прямой угол.

10. Основные требования предъявляемые к проекционным изображениям

Обратимость – восстановление оригинала по его проекционным
изображениям (чертежу) – возможность определять форму и размеры
объекта, его положение и связь с окружающей средой
Наглядность – чертеж должен создавать пространственное
представление о форме предмета
Точность – графические операции, выполненные на чертеже, должны
давать достаточно точные результаты
Простота – изображение должно быть простым по построению и
должно допускать однозначное описание объекта в виде
последовательности графических операций