Похожие презентации:
Цилиндр, конус и шар
1. Цилиндр, конус и шар
ПонятиеПлощадь поверхности
2. Цилиндр
Дано:α || β, окружность L
(О; r),
расположенная в
плоскости α.
Проведем из каждой
точки L отрезки,
перпендикулярные
к плоскости α
О
α
β
3. Цилиндр
Отрезки прямых,заключенные
между
параллельными
плоскостями α и
β, образуют
цилиндрическую
поверхность
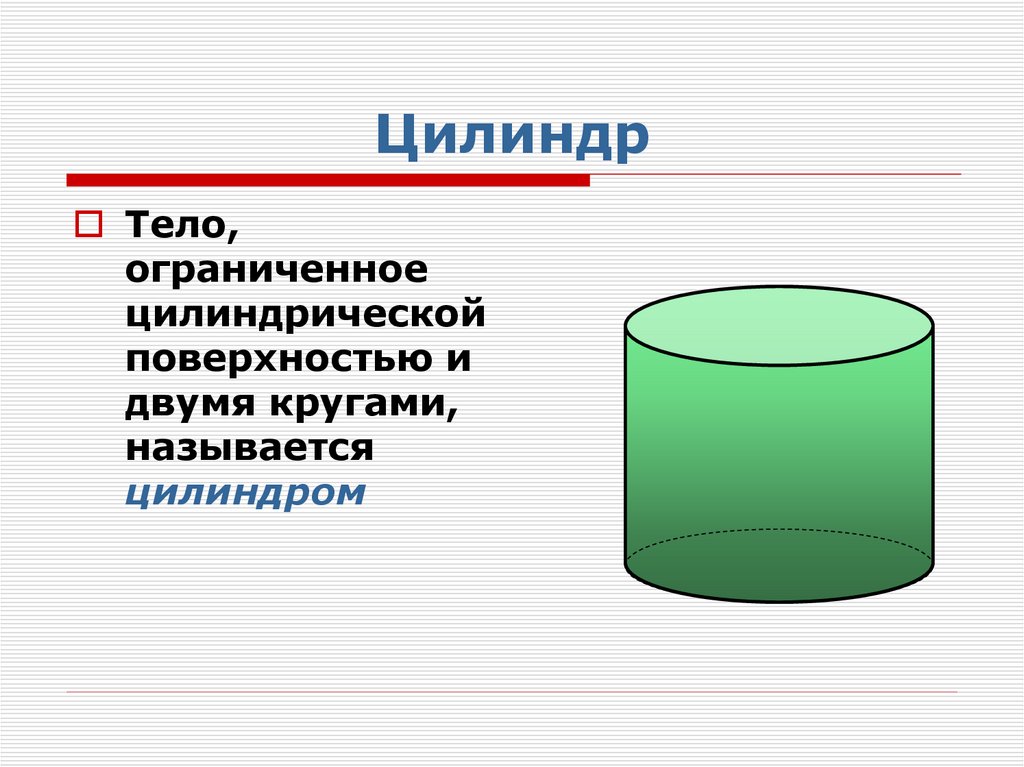
4. Цилиндр
Тело,ограниченное
цилиндрической
поверхностью и
двумя кругами,
называется
цилиндром
5. Цилиндр
6. Цилиндр
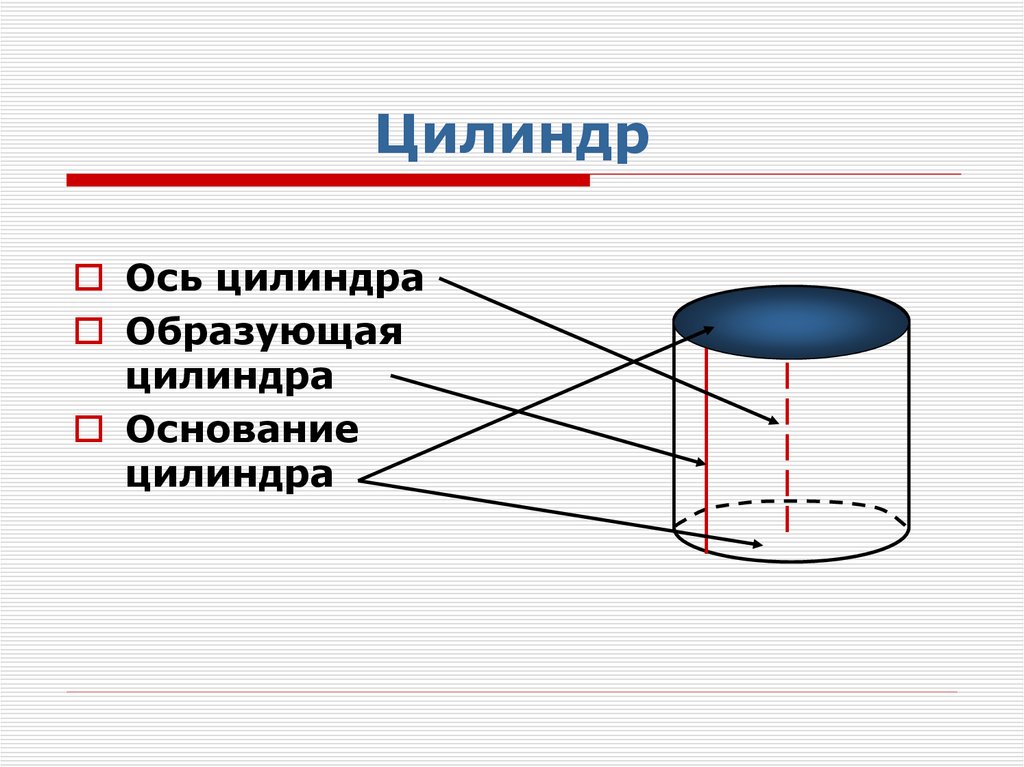
Ось цилиндраОбразующая
цилиндра
Основание
цилиндра
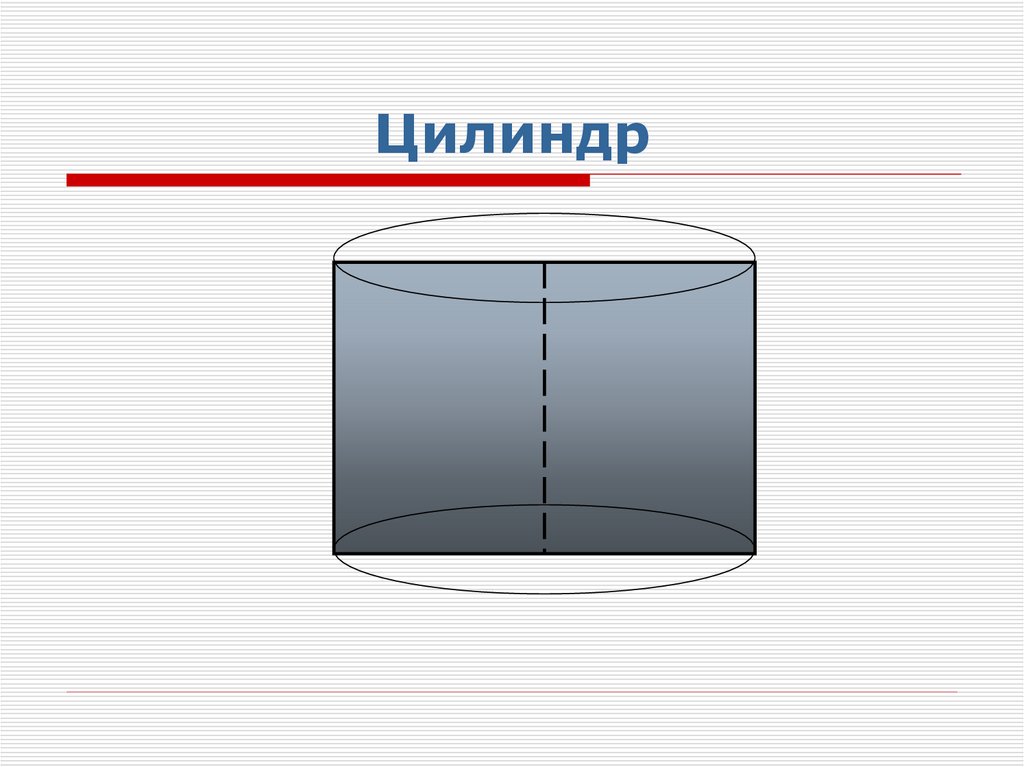
7.
Осевоесечение
Сечение плоскостью,
перпендикулярной оси
8. Площадь боковой поверхности цилиндра
Площадьбоковой
поверхности
цилиндра равна
произведению
длины
окружности
основания на
высоту
цилиндра
r
h
Sбок = 2πrh
9. Площадь полной поверхности цилиндра
Площадьюполной
поверхности
цилиндра
называется
сумма площадей
боковой
поверхности и
двух оснований
S = 2πr2 + 2πrh
или
S = 2πr(r + h)
10. Развертка цилиндра
rh
2πr
11. Конус
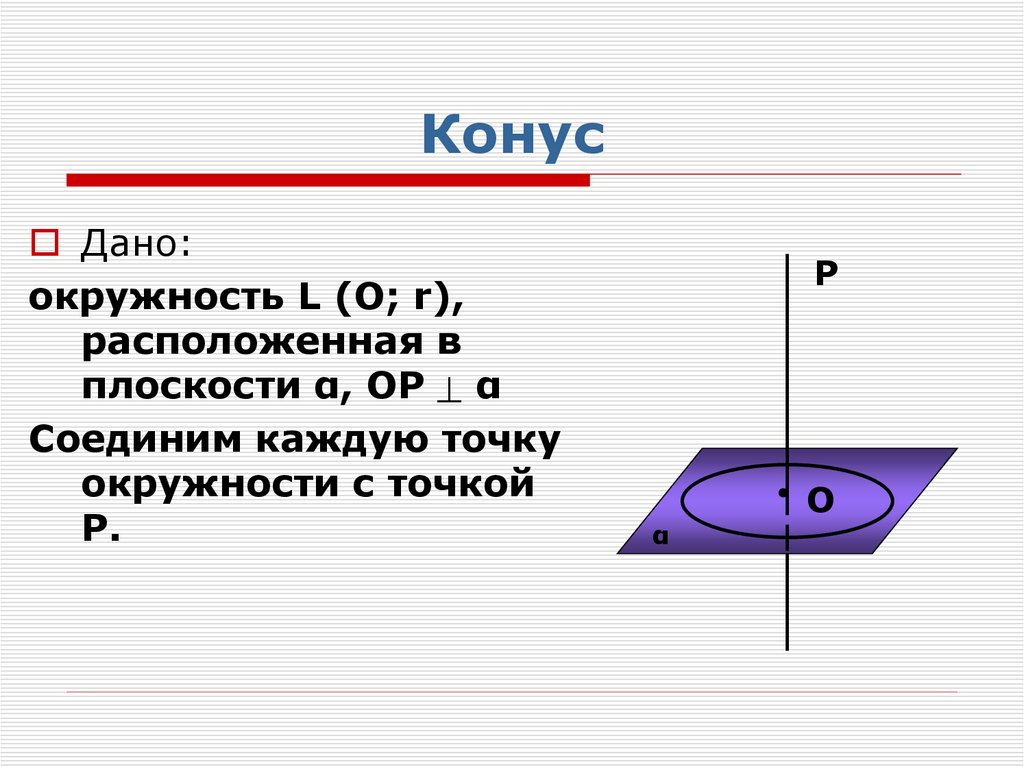
Дано:окружность L (О; r),
расположенная в
плоскости α, ОР α
Соединим каждую точку
окружности с точкой
Р.
Р
α
О
12. Конус
Поверхность,образованная
отрезками,
соединяющими
каждую точку
окружности с
точкой на прямой
ОР, называется
конической
поверхностью
13. Конус
Тело,ограниченное
конической
поверхностью и
кругом с
границей L,
называется
конусом
14. Конус
15. Конус
Основаниеконуса
Ось конуса
Образующая
конуса
Вершина конуса
16. Площадь поверхности конуса
Площадьбоковой
поверхности
конуса равна
произведению
половины
длины
окружности
основания на
образующую
l
r
Sбок = πrl
17.
Площадь полнойповерхности
конуса равна
сумме площадей
боковой
поверхности и
основания
S = πr2 + πrl
или
S = πr(r + l)
18.
Сечениеплоскостью,
перпендикулярной
оси конуса
Осевое сечение
19. Сфера и шар
Поверхность,состоящая из
всех точек
пространства,
расположенных
на данном
расстоянии от
данной точки,
называется
сферой
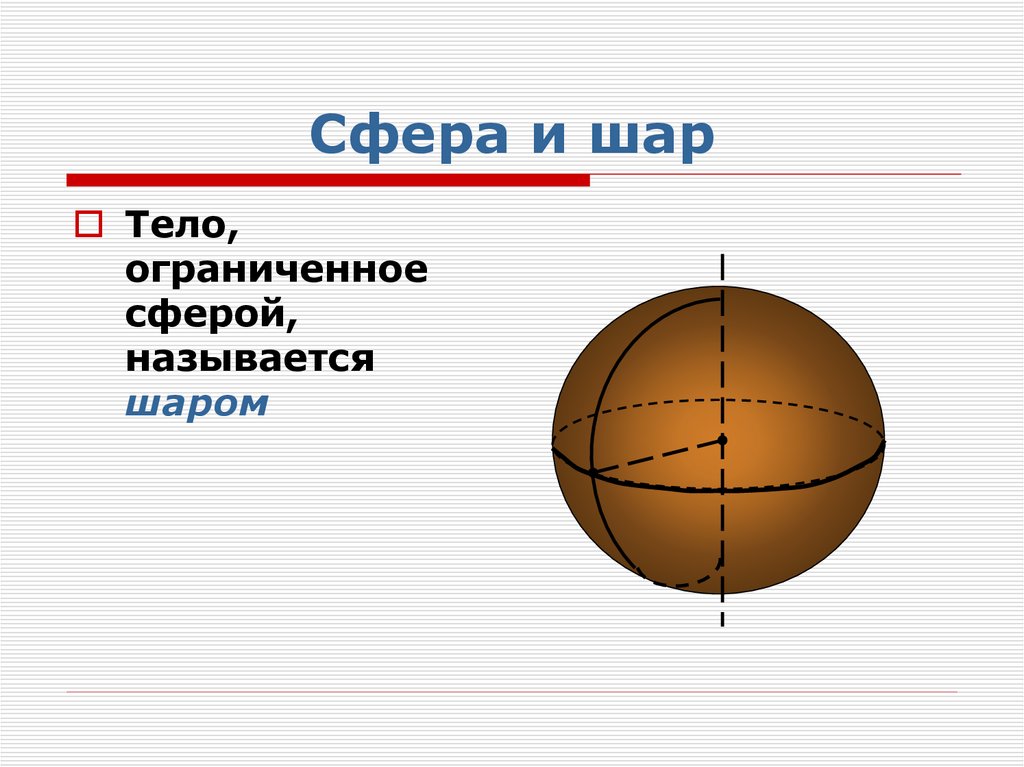
20. Сфера и шар
Тело,ограниченное
сферой,
называется
шаром
21. Сфера и шар
Дано:Сфера радиуса R с
центром С (х0; у0; z0),
точка М (х; у; z)
лежит на сфере.
Чему равно расстояние
МС?
М
С
22. Уравнение сферы
Т. к. МС = R, то( х х0 ) ( у у0 ) ( z z0 ) R
2
2
2
2
23. Взаимное расположение сферы и плоскости
Дано: плоскость α,сфера (С; R),
d - расстояние от
центра С до
плоскости α.
Введем систему
координат, где
точка С (x0;y0;z0).
Составим
уравнения сферы и
плоскости α.
z
M
C
у
х
24. Взаимное расположение сферы и плоскости
Пусть точка С лежит на оси z. Тогда еекоординаты (0; 0; d).
Уравнение сферы:
x y z d R
2
2
Уравнение плоскости α: z = 0
Исследуем систему уравнений:
2
2
25.
Взаимное расположениесферы и плоскости
x y z d R
2
2
2
z=0
Тогда
x y R d
2
2
2
2
2
26. Взаимное расположение сферы и плоскости
1) d < R.Тогда
x y R d
2
2
2
- уравнение
окружности (О; r)
Сечение сферы
плоскостью окружность
2
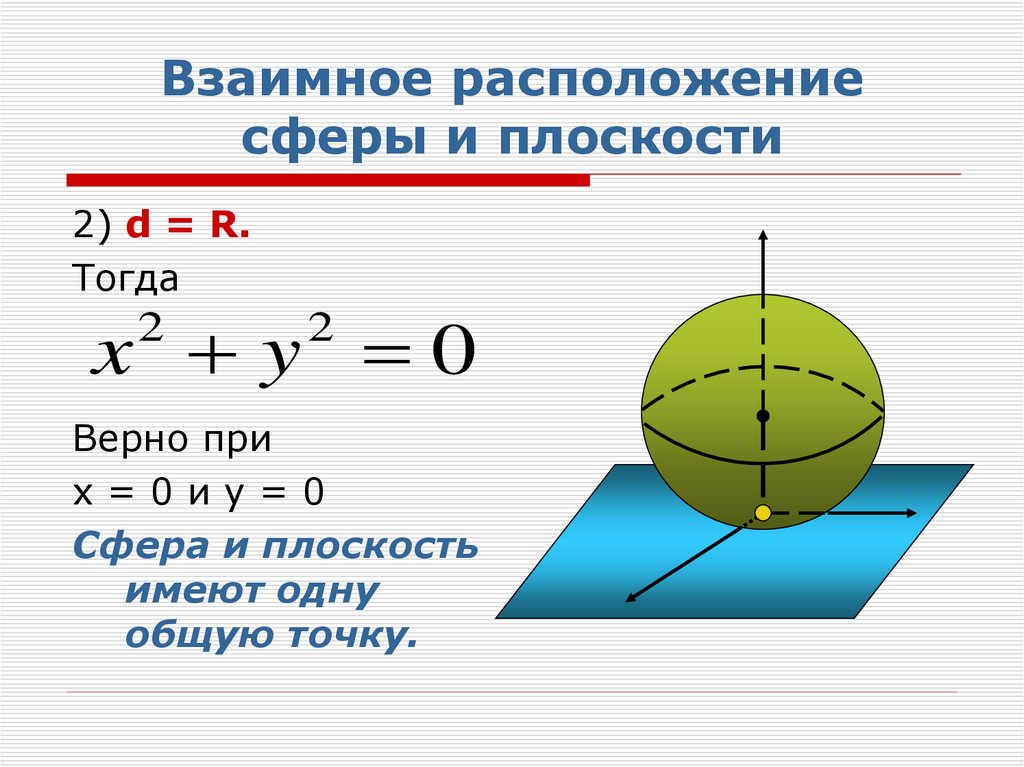
27. Взаимное расположение сферы и плоскости
2) d = R.Тогда
x y 0
2
2
Верно при
х=0иу=0
Сфера и плоскость
имеют одну
общую точку.
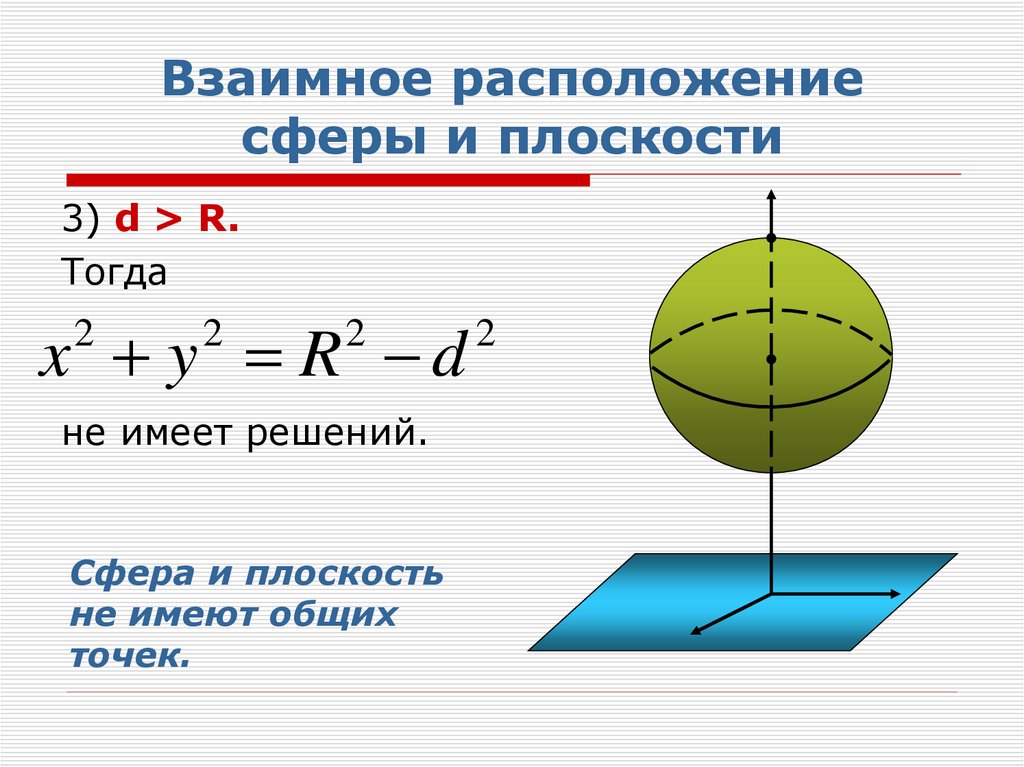
28. Взаимное расположение сферы и плоскости
3) d > R.Тогда
x y R d
2
2
2
не имеет решений.
Сфера и плоскость
не имеют общих
точек.
2





















 Математика
Математика








