Основы теории графов

1. Основы теории графов

2.

3.

…Всё, что без этого было темно, сомнительно и
неведомо, математика сделала ясным, верным и
очевидным…
Густав Роберт Кирхгоф
Леонард
Эйлер
Артур Кэли
Уильям Роуэн
Гамильтон
Освальд Веблен
Мёбиус Карл Август
Андрей Андреевич
Марков
Джордж
Юджин Уленбек

4.

5.

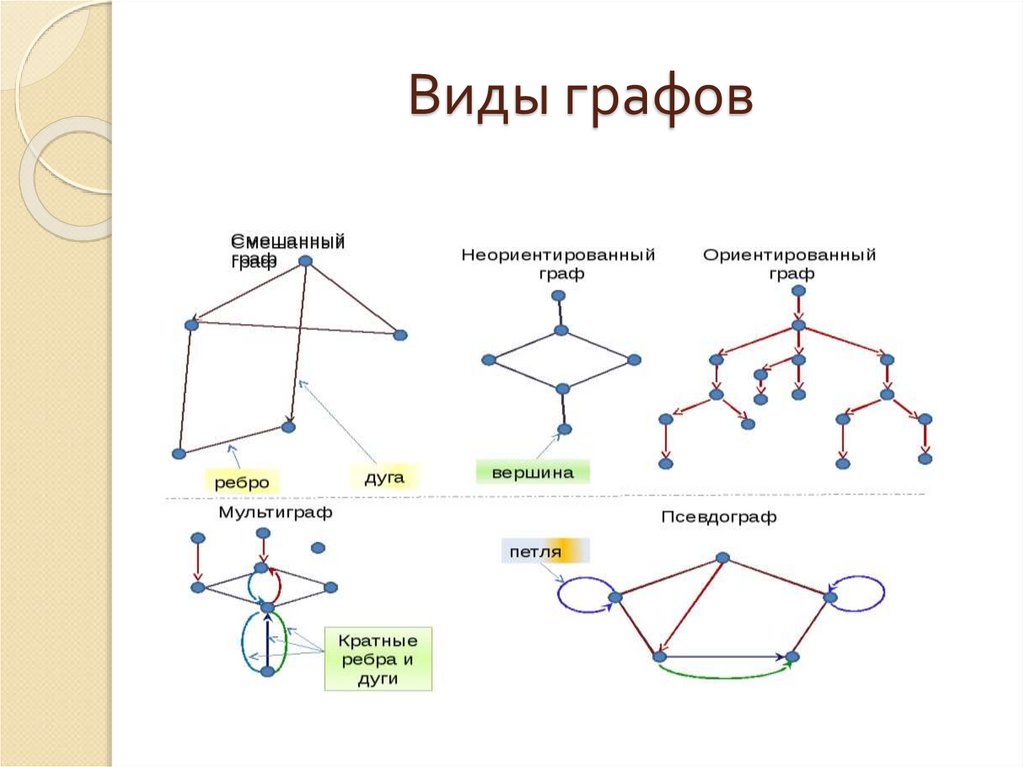
6. Виды графов

7.

8.

Бывший Кенигсберг (ныне Калининград) расположен
на реке Прегель. В пределах города река омывает
два острова. С берегов на острова были перекинуты
мосты. Старые мосты не сохранились, но осталась
карта города, где они изображены.

9.

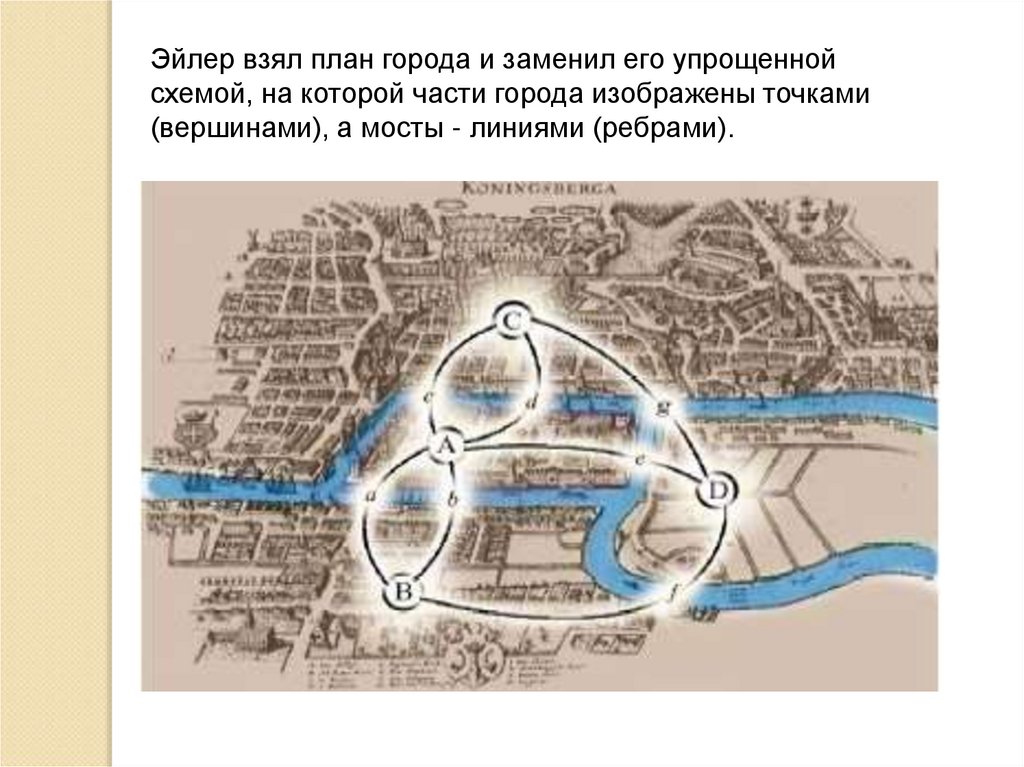
Эйлер взял план города и заменил его упрощенной
схемой, на которой части города изображены точками
(вершинами), а мосты - линиями (ребрами).

10.

11. Одним росчерком

Если все вершины
графа четные, то
можно не отрывая
карандаш от бумаги
(«одним росчерком»),
проводя по каждому
ребру только один
раз, начертить этот
граф. Движение
можно начать с
любой вершины и
закончить его в той
же вершине.

12. Одним росчерком

Граф, имеющий
всего две нечетные
вершины, можно
начертить, не
отрывая карандаш
от бумаги, при этом
движение нужно
начать с одной из
этих нечетных
вершин и закончить
во второй из них.

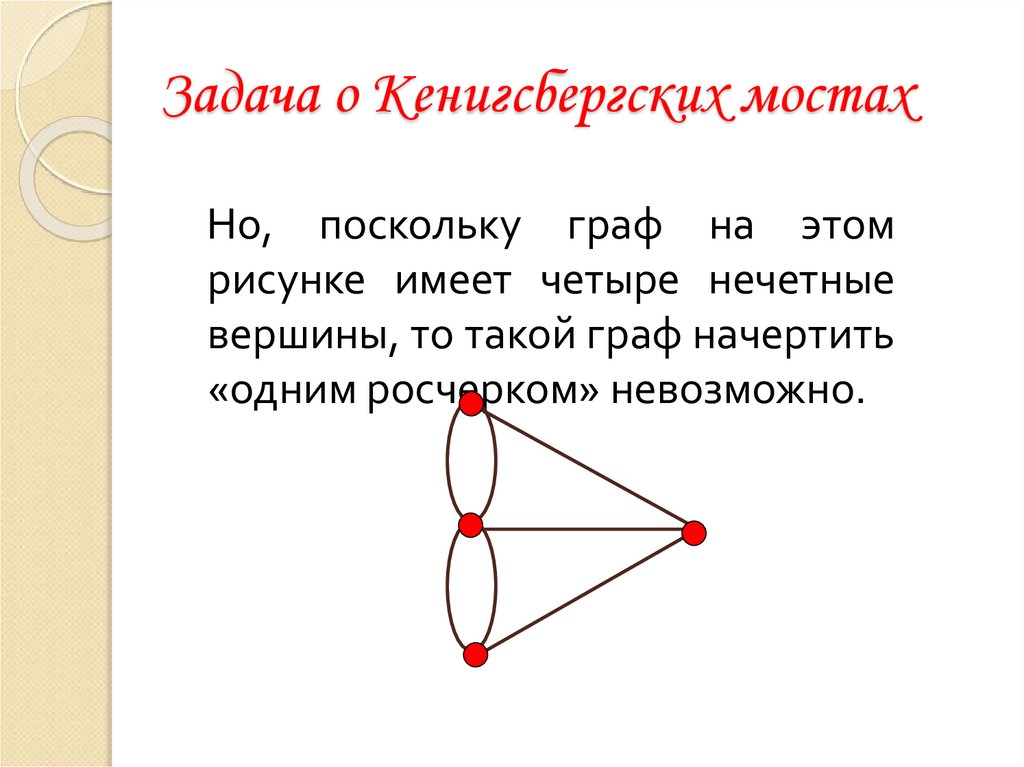
13. Задача о Кенигсбергских мостах

Но, поскольку граф на этом
рисунке имеет четыре нечетные
вершины, то такой граф начертить
«одним росчерком» невозможно.

14.

15.

16.

17.

18.

19.

20.

21. Задача: В графе (Рис. 1) найти длину кратчайшего пути из Х4 в Х1

22.

23.

24.

25.

26. Проблема четырех красок

Выяснить, можно
ли всякую
расположенную на
сфере карту
раскрасить
четырьмя
красками так,
чтобы любые две
области, имеющие
общий участок
границы, были
раскрашены в
разные цвета.

27. Хроматическое число плоского графа не превосходит 4

Применение на практике
Хроматическое число
плоского графа не превосходит 4

28. Задача коммивояжёра

одна из самых известных
задач комбинаторной
оптимизации,
заключающаяся в
отыскании самого
выгодного маршрута,
проходящего через
указанные города хотя
бы по одному разу с
последующим возвратом
в исходный город.

29. Определение расстояний между станциями

Применение на практике
Определение расстояний между
станциями

30. Сетевой график

Применение на практике
Сетевой график

31. Составление графика на дисциплине «Технология перевозочного процесса»

Применение на практике
Составление графика на дисциплине «Технология
перевозочного процесса»