Linear Algebra. Chapter 1. Matrix Algebra

1. Chapter 2 Matrix Algebra

Linear Algebra
Chapter 2
Matrix Algebra

2. 2.1 Addition, Scalar Multiplication, and Multiplication of Matrices

• aij: the element of matrix A in row i and column j.
• For a square n n matrix A, the main diagonal is:
a11 a12
a
a22
21
A
an1 an 2
a1n
a2 n
ann
Definition
Two matrices are equal if they are of the same size and if their
corresponding elements are equal.
Thus A = B if aij = bij i, j.
( for every, for all)
Ch2_2

3. Addition of Matrices

Definition
Let A and B be matrices of the same size.
Their sum A + B is the matrix obtained by adding together the
corresponding elements of A and B.
The matrix A + B will be of the same size as A and B.
If A and B are not of the same size, they cannot be added, and we
say that the sum does not exist.
Thus if C A B, then cij aij bij i,j .
Ch2_3

4. Example 1

4 7 , B 2 5 6 , and C 5 4 .
Let A 1
8
0 2 3
3 1
2 7
Determine A + B and A + C, if the sum exist.
Solution
4 7 2 5 6
(1) A B 1
8
0 2 3 3 1
4 5 7 6
1 2
0 3 2 1 3 8
3 9 1 .
3 1 11
(2) Because A is 2 3 matrix and C is a 2 2 matrix, they are
not of the same size, A + C does not exist.
Ch2_4

5. Scalar Multiplication of matrices

Definition
Let A be a matrix and c be a scalar. The scalar multiple of A by c,
denoted cA, is the matrix obtained by multiplying every element
of A by c. The matrix cA will be the same size as A.
Thus if B cA, then bij caij i, j.
Example 2
1 2 4
Let A
.
7 3 0
3 1 3 ( 2) 3 4 3 6 12
3A
.
3 7 3 ( 3) 3 0 21 9 0
Observe that A and 3A are both 2 3 matrices.
Ch2_5

6. Negation and Subtraction

Definition
We now define subtraction of matrices in such a way that makes it
compatible with addition, scalar multiplication, and negative. Let
A – B = A + (–1)B
Example 3
Suppose A 5 0 2 and B 2 8 1 .
3 6 5
0 4 6
5 2 0 8 2 ( 1) 3 8 1
A B
.
2 11
3 0 6 4
5 6 3
Ch2_6

7. Multiplication of Matrices

Definition
Let the number of columns in a matrix A be the same as the
number of rows in a matrix B. The product AB then exists.
Let A: m n matrix, B: n k matrix,
The product matrix C=AB has elements
cij ai1
ai 2
b1 j
b
2j
ain
ai1b1 j ai 2b2 j ainbnj
bnj
C is a m k matrix.
If the number of columns in A does not equal the number of row B,
we say that the product does not exist.
Ch2_7

8. Example 4

0 1
1 3
5
Let A
,B
, and C 6 2 5 .
2 0
3 2 6
Determine AB, BA, and AC, if the products exist.
Solution.
AB 1
2
5
1 3
3
5
2
0
3
3 5
0
3
0
2
0
1 3
2
0
2 0
2
1
6
1
1 3
6
1
2 0
6
(1 5) (3 3) (1 0) (3 ( 2)) (1 1) (3 6)
(2 5) (0 3) (2 0) (0 ( 2)) (2 1) (0 6)
14 6 19
.
10
0
2
BA and AC do not exist.
Note. In general, AB BA.
Ch2_8

9. Example 5

1
2
Let A 7
0 and B 1 0 . Determine AB.
3 5
3 2
2 1 1
2 1 0
3
5
1
2
1
0
1
0
7 0 5
AB 7
0
7 0
3
5
3
3 2
1
0
3 2
3 2
3
5
5
2 3 0 5 1
7 0 0 0 7
0
3 6 0 10 3 10
Example 6
Let C = AB, A 2 1 and B 7 3 2 Determine c23.
3 4
5 0 1
2 ( 3 2) (4 1) 2
3
4
c23
1
Ch2_9

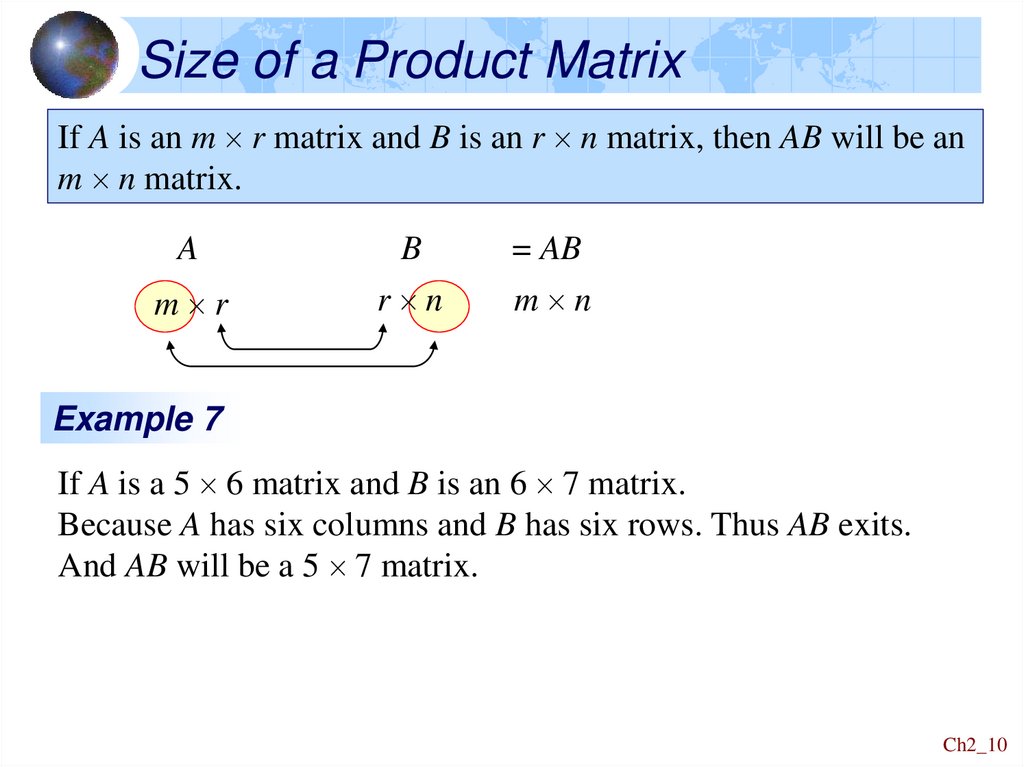
10. Size of a Product Matrix

If A is an m r matrix and B is an r n matrix, then AB will be an
m n matrix.
A
B
= AB
m r
r n
m n
Example 7
If A is a 5 6 matrix and B is an 6 7 matrix.
Because A has six columns and B has six rows. Thus AB exits.
And AB will be a 5 7 matrix.
Ch2_10

11.

Special Matrices
Definition
A zero matrix is a matrix in which all the elements are zeros.
A diagonal matrix is a square matrix in which all the elements
not on the main diagonal are zeros.
An identity matrix is a diagonal matrix in which every diagonal
element is 1.
0 0 0
0mn 0 0 0
0 0 0
zero matrix
a11 0
0 a
22
A
0
0
0
0
ann
1 0 0
I n 0 1 0
0 0 1
identity matrix
diaginal matrix A
Ch2_11

12. Theorem 2.1

Let A be m n matrix and Omn be the zero m n matrix. Let B be
an n n square matrix. On and In be the zero and identity n n
matrices. Then
A + Omn = Omn + A = A
BOn = OnB = On
BIn = InB = B
Example 8
Let A 2 1 3 and B 2 1 .
8
4 5
3 4
2
A O23
4
1 3
0 0
1 3
5
0
5
0
8 0
2
0 4
2 1 0 0 0 0
BO2
O2
3 3 0 0 0 0
2 1 1 0 2 1
B
BI 2
3 4 0 1 3 4
A
8
Ch2_12

13. Homework

Exercises will be given by the teachers of the
practical classes.
Exercise
Let A be a matrix whose third row is all zeros. Let B be any
matrix such that the product AB exists.
Prove that the third row of AB is all zeros.
Solution
b1i
b1i
b
b
( AB) 3i [a31 a32 a3n ] 2i [0 0 0] 2i 0, i.
bni
bni
Ch2_13

14. 2.2 Algebraic Properties of Matrix Operations

Theorem 2.2 -1
Let A, B, and C be matrices and a, b, and c be scalars. Assume that the
size of the matrices are such that the operations can be performed.
Properties of Matrix Addition and scalar Multiplication
1. A + B = B + A
Commutative property of addition
2. A + (B + C) = (A + B) + C Associative property of addition
3. A + O = O + A = A
(where O is the appropriate zero matrix)
4. c(A + B) = cA + cB
Distributive property of addition
5. (a + b)C = aC + bC
Distributive property of addition
6. (ab)C = a(bC)
Ch2_14

15.

Theorem 2.2 -2
Let A, B, and C be matrices and a, b, and c be scalars. Assume that the
size of the matrices are such that the operations can be performed.
Properties of Matrix Multiplication
1. A(BC) = (AB)C
Associative property of multiplication
2. A(B + C) = AB + AC
Distributive property of multiplication
3. (A + B)C = AC + BC
Distributive property of multiplication
4. AIn = InA = A
(where In is the appropriate identity matrix)
5. c(AB) = (cA)B = A(cB)
Note: AB BA in general.
Multiplication of matrices is not
commutative.
Ch2_15

16.

Proof of Theorem 2.2 (A+B=B+A)
Consider the (i,j)th elements of matrices A+B and B+A:
( A B)ij aij bij bij aij ( B A)ij .
A+B=B+A
Example 9
Let A 1 3 , B 3 7 , and C 0 2 .
1
4 5
8
5 1
A B C 1 3 3 7 0 2
1 5 1
4 5 8
1 3 0 3 7 2 4 6 .
5
4 8 5 5 1 1 9
Ch2_16

17. Arithmetic Operations

If A is an m r matrix and B is r n matrix, the number of scalar
multiplications involved in computing the product AB is mrn.
Consider three matrices A, B and C such that the product
ABC exists.
Compare the number of multiplications involved in the
two ways (AB)C and A(BC) of computing the product ABC
Ch2_17

18. Example 10

4
3 , and C 1 .
Let A 1 2 , B 0 1
Compute ABC.
3 1
1 0 2
0
Solution.
Which method is better?
Count the number of multiplications.
(1) (AB)C
3 2 1 1 .
AB 1 2 0 1
3 1 1 0 2 1 3 11
2 6+3 2
4 9
=12+6=18
2
1
1
1 .
( AB)C
1 3 11 0 1
(2) A(BC)
4
0
1
3
1 1
BC
1 0 2 0 4
A( BC ) 1 2 1 9 .
3 1 4 1
3 2+2 2
=6+4=10
A(BC) is better.
Ch2_18

19.

Caution
In algebra we know that the following cancellation laws apply.
If ab = ac and a 0 then b = c.
If pq = 0 then p = 0 or q = 0.
However the corresponding results are not true for matrices.
AB = AC does not imply that B = C.
PQ = O does not imply that P = O or Q = O.
Example 11
1 2
1 2
3 8
(1) Consider t he matrices A
, B 2 1 , and C 3 2 .
2
4
3 4
Observe that AB AC
, but B C.
6 8
1 2
2 6
(2) Consider t he matrices P
, and Q
.
4
2
1 3
Observe that PQ O, but P O and Q O.
Ch2_19

20. Powers of Matrices

Definition
If A is a square matrix, then
Ak
AA
A
k times
Theorem 2.3
If A is an n n square matrix and r and s are nonnegative
integers, then
1. ArAs = Ar+s.
2. (Ar)s = Ars.
3. A0 = In (by definition)
Ch2_20

21. Example 12

1 2
4
If A
,
compute
A
.
0
1
Solution
1 2 1 2 3 2
A
1
0
1
0
1
2
2
3 2 3 2 11 10
A
.
2 1
2 5
6
1
4
Example 13 Simplify the following matrix expression.
A( A 2 B ) 3B ( 2 A B ) A2 7 B 2 5 AB
Solution
A( A 2 B) 3B (2 A B ) A2 7 B 2 5 AB
A2 2 AB 6 BA 3B 2 A2 7 B 2 5 AB
3 AB 6 BA 4 B 2
We can’t add the two matrices
Ch2_21

22. Systems of Linear Equations

A system of m linear equations in n variables as follows
a11 x1 a1n xn b1
am1 x1 amn xn bm
Let
a11 a1n
x1
b1
A , X , and B
am1 amn
xn
bm
We can write the system of equations in the matrix form
AX = B
Ch2_22

23. Idempotent and Nilpotent Matrices

Definition
(1) A square matrix A is said to be idempotent if A2=A.
(2) A square matrix A is said to nilpotent if there is a
p
positive integer p such that A =0. The least integer p such that
Ap=0 is called the degree of nilpotency of the matrix.
Example 14
3 6 2 3 6
(1) A
,A
A.
1 2
1 2
3 9 2 0 0
(2) B
,B
. The degree of nilpotency : 2
1 3
0 0
Ch2_23

24. Homework

Exercises will be given by the teachers
of the practical classes.
Ch2_24

25. 2.3 Symmetric Matrices

Definition
The transpose of a matrix A, denoted At, is the matrix whose
columns are the rows of the given matrix A.
i.e., A : m n At : n m, ( At )ij Aji i, j.
Example 15
A 2 7 , B 1 2 7 , and C 1 3 4 .
6
8 0
4 5
1
1
4
t
t
C 3 .
At 2 8
B
2
5
0
7
4
7 6
Ch2_25

26. Theorem 2.4: Properties of Transpose

Let A and B be matrices and c be a scalar. Assume that the sizes
of the matrices are such that the operations can be performed.
1. (A + B)t = At + Bt
Transpose of a sum
2. (cA)t = cAt
Transpose of a scalar multiple
3. (AB)t = BtAt
Transpose of a product
4. (At)t = A
Ch2_26

27. Symmetric Matrix

Definition
A symmetric matrix is a matrix that is equal to its transpose.
A At , i.e., aij a ji i, j
Example 16
5
2
5 4
match
1
0 1 4 0
8
1 7
2
4 8 3 4
0 2
4
7
3
9
3
2 3
9 3
6
match
Ch2_27

28. Remark: If and only if

Let p and q be statements.
Suppose that p implies q (if p then q), written p q,
and that also q p, we say that
“p if and only if q” (in short iff )
Ch2_28

29. Example 17

Let A and B be symmetric matrices of the same size. Prove that
the product AB is symmetric if and only if AB = BA.
Proof
*We have to show (a) AB is symmetric AB = BA,
and the converse, (b) AB is symmetric AB = BA.
( ) Let AB be symmetric, then
AB= (AB)t
by definition of symmetric matrix
= BtAt
by Thm 2.4 (3)
= BA
since A and B are symmetric
( ) Let AB = BA, then
(AB)t = (BA)t
= AtBt
by Thm 2.4 (3)
= AB
since A and B are symmetric
Ch2_29

30. Example 18

Let A be a symmetric matrix. Prove that A2 is symmetric.
Proof
( A ) ( AA) ( A A ) AA A
2 t
t
t
t
2
Ch2_30

31. Homework

Exercises will be given by the teachers of
the practical classes.

32. 2.4 The Inverse of a Matrix

Definition
Let A be an n n matrix. If a matrix B can be found such that
AB = BA = In, then A is said to be invertible and B is called the
inverse of A. If such a matrix B does not exist, then A has no
inverse. (denote B = A 1, and A k=(A 1)k )
Example 19
2 1
Prove that the matrix A 1 2 has inverse B 3 1 .
3 4
2
2
Proof
1 1 0
2
1
2
1
AB
I
3 4 32 2 0 1 2
1 1 2 1 0
2
BA 3 1
I2
3
4
0
1
2
2
Thus AB = BA = I2, proving that the matrix A has inverse B.
Ch2_32

33. Theorem 2.5

The inverse of an invertible matrix is unique.
Proof
Let B and C be inverses of A.
Thus AB = BA = In, and AC = CA = In.
Multiply both sides of the equation AB = In by C.
C(AB) = CIn
Thm2.2
(CA)B = C
InB = C
B=C
Thus an invertible matrix has only one inverse.
Ch2_33

34. Gauss-Jordan Elimination for finding the Inverse of a Matrix

Let A be an n n matrix.
1. Adjoin the identity n n matrix In to A to form the matrix
[A : In].
2. Compute the reduced echelon form of [A : In].
If the reduced echelon form is of the type [In : B], then B is
the inverse of A.
If the reduced echelon form is not of the type [In : B], in that
the first n n submatrix is not In, then A has no inverse.
An n n matrix A is invertible if and only if its reduced echelon
form is In.
Ch2_34

35. Example 20

1 1 2
Determine the inverse of the matrix A 2 3 5
3
5
1
Solution
1 1 2 1 0 0
1
[ A : I 3 ] 2 3 5 0 1 0 R2 ( 2) R1 0
3
5 0 0 1 R3 R1 0
1
1 1 2 1 0 0
1
( 1)R2 0
1
1 2 1 0 R1 R2 0
3 1 0 1 R3 ( 2)R2 0
0 2
1 0 0
0
1
1
R1 R3 0 1 0 5 3 1
R2 ( 1)R3 0 0 1 3 2 1
1 1
0
Thus, A 5 3 1 .
2
1
3
1 2
1 0 0
1 1 2 1 0
2
3
1 0 1
0 1
3 1 0
1 1
2 1 0
0
1 3 2 1
1
Ch2_35

36. Example 21

Determine the inverse of the following matrix, if it exist.
1 1 5
A 1 2 7
2 1 4
Solution
1
5
1 0 0
1 1 5 1 0 0
1
[ A : I 3 ] 1 2 7 0 1 0 R2 ( 1)R1 0
1
2 1 1 0
2 1 4 0 0 1 R3 ( 2)R1 0 3 6 2 0 1
2 1 0
1 0 3
R1 ( 1)R2 0 1 2 1 1 0
R3 3R2 0 0 0 5 3 1
There is no need to proceed further.
The reduced echelon form cannot have a one in the (3, 3) location.
The reduced echelon form cannot be of the form [In : B].
Thus A–1 does not exist.
Ch2_36

37. Properties of Matrix Inverse

Let A and B be invertible matrices and c a nonzero scalar, Then
1. ( A 1 ) 1 A
1 1
1
2. (cA) A
c 1 1
1
3. ( AB) B A
4. ( An ) 1 ( A 1 ) n
5. ( At ) 1 ( A 1 ) t
Proof
1. By definition, AA 1=A 1A=I.
2. (cA)( 1c A 1 ) I ( 1c A 1 )(cA)
3. ( AB)( B 1 A 1 ) A( BB 1 ) A 1 AA 1 I ( B 1 A 1 )( AB)
1
1
1 n n
4. An ( A 1 ) n
A
A
A
A
I
(
A
) A
n times
n times
5. AA 1 I , ( AA 1 ) t ( A 1 ) t At I ,
A 1 A I , ( A 1 A) t At ( A 1 ) t I ,
Ch2_37

38.

Example 22
If A 4 1 , then it can be shown that A 1 1 1 . Use this
3 1
3 4
informatio n to compute ( At ) 1.
Solution
t
1 1
1 3
(A ) (A )
.
3 4 1 4
t 1
1 t
Ch2_38

39. Theorem 2.6

Let AX = B be a system of n linear equations in n variables.
If A–1 exists, the solution is unique and is given by X = A–1B.
Proof
(X = A–1B is a solution.)
Substitute X = A–1B into the matrix equation.
AX = A(A–1B) = (AA–1)B = In B = B.
(The solution is unique.)
Let Y be any solution, thus AY = B. Multiplying both sides of this
equation by A–1 gives
A–1A Y= A–1B
In Y= A–1B
Y = A–1B. Then Y=X .
Ch2_39

40. Example 22

x1 x2 2 x3 1
Solve the system of equations 2 x1 3 x2 5 x3 3
x1 3 x2 5 x3 2
Solution
This system can be written in the following matrix form:
1 1 2 x1 1
2 3 5 x2 3
3
5 x3 2
1
If the matrix of coefficients is invertible, the unique solution is
1
x1 1 1 2 1
x2 2 3 5 3
x 1
3
5 2
3
This inverse has already been found in Example 20. We get
x1 0
1 1 1 1
x2 5 3 1 3 2
x 3
2
1 2 1
3
The unique solution is x1 1, x2 2, x3 1.
Ch2_40

41. Elementary Matrices

Definition
An elementary matrix is one that can be obtained from the
identity matrix In through a single elementary row operation.
Example 23
1 0 0
I 3 0 1 0
0 0 1
R2 R3
5R2
R2+ 2R1
1 0 0
E1 0 0 1
0 1 0
1 0 0
E2 0 5 0
0 0 1
1 0 0
E3 2 1 0
0 0 1
Ch2_41

42. Elementary Matrices

。 Elementary row operation
。 Elementary matrix
a
g
R2 R3
d
a
A d
g
b
e
h
c
f
i
5R2
a
5d
g
c 1 0 0
i 0 0 1 A E1 A
f 0 1 0
b
h
e
c 1 0 0
5e 5 f 0 5 0 A E2 A
h
i 0 0 1
b
b
a
d 2a e 2b
R2+ 2R1
g
h
1 0 0
f 2c 2 1 0 A E3 A
i 0 0 1
c
Ch2_42

43. Notes for elementary matrices

Each elementary matrix is invertible.
Example 24
I E1 E1 I , i.e., E2 E1 I
R1 2 R 2
R1 2 R 2
1 0 0
I 0 1 0
0 0 1
1 2 0
E1 0 1 0
0 0 1
1 2 0
E2 0 1 0
0 0 1
If A and B are row equivalent matrices and A is
invertible, then B is invertible.
Proof
If A … B, then
B=En … E2 E1 A for some elementary matrices En, … , E2 and E1.
So B 1 = (En … E2 E1A) 1 =A 1E1 1 E2 1 … En 1.
Ch2_43

44. Homework

Exercises will be given by the teachers of the practical
classes.
Exercise
d b
1
a b
1
.
If A
, show that A
(ad bc) c a
c d
Ch2_44