Похожие презентации:
Машины Тьюринга-Поста. Абстрактная модель алгоритма
1. Машины Тьюринга-Поста
Машины ТьюрингаПостаАбстрактная модель алгоритма
(1936-1937)
2.
А́лан Мэ́тисон Тью́рингAlan Mathison Turing
1912-1954
английский математик,
логик, криптограф (Энигма)
«Алан Тьюринг - взломщик кодов и пионер
информатики».
Общепринято считать Алана Тьюринга
отцом
информатики
и
теории
искусственного интеллекта.
3.
Премия Тьюринга (Turing Award) - самаяпрестижная премия в информатике, вручаемая
Ассоциацией вычислительной
техники за выдающийся научно-технический
вклад в этой области.
В настоящее время премия спонсируется
корпорациями Intel и Google и составляет
250 000 долларов США.
Лауреаты премии Тьюринга
Р. Хэмминг, Н. Вирт, Д. Кнут,
Э. Дейкстра , Д. Грэй, Д. Перл, Ч. Теккер…..
4. Символьные конструкции
Алфавит- любое конечное множество
попарно различных знаков, называемых
буквами (символами) этого алфавита.
Алфавит будем обозначать заглавными
буквами, например:
Символом - обозначение пустого символа.
5.
Слово в данном алфавите - любая конечная(в том числе и пустая) последовательность
букв этого алфавита.
Слова обозначаются малыми греческими
буквами.
Например:
= algorithm - слово в алфавите А;
= 1010100 - слово в алфавите В;
0 0 - слово в алфавите С.
Пустое слово обозначим .
6.
Длина слова (обозначается ) - этоколичество букв в слове.
Отношения и операции над словами
Равенство слов в алфавите А определяется
индуктивно:
а) пустые слова равны;
б) если слово равно слову , то
b = b , где b - буква в алфавите А.
7.
слово является частью слова валфавите A, то слово – подслово слова
(или слово входит в слово ).
Если
Например: в слове 1012011201
два
вхождения слова 12, три вхождения слова
01, одиннадцать вхождений пустого слова
- перед первой, после последней букв и
,
между всеми буквами.
8.
Слово длины n , составленное из буквы а,повторенной n раз, будем обозначать
Например xyxxxyyyy =
xyx3y. 4
n
a .
9. Классическая машина Тьюринга Основные определения
Подмашиной
Тьюринга
понимается
гипотетическая
(абстрактная)
машина,
состоящая из следующих частей:
1) потенциально бесконечной в обе стороны
ленты, разбитой на ячейки, в каждой ячейке
может быть записан только один символ из
алфавита
A a1 , a2 ,....,an ,
а также пустой символ ;
10.
УУуправляющего устройства
(рабочей головки), которое в каждый
момент времени может находится в одном
из состояний множества
2)
В
-
каждом
из
состояний
головка
размещается напротив ячейки и может
считывать (обозревать) или записывать в
нее букву из алфавита А.
11. Классическая машина Тьюринга
Часть ленты, в которой записаны буквыалфавита А - рабочая зона.
...
a1
...
aj
qi
...
ak
...
12. Функционирование КМТ
состоитиз
последовательности
элементарных шагов (тактов).
На каждом шаге выполняются следующие
действия:
a j;
1) УУ считывает символ
qi
2) в зависимости от своего состояния
и считанного символа ленты a j УУ
a j A
вырабатывает символ
и записывает его в обозреваемую ячейку,
возможно a j a j;
13.
3) УУ перемещается на одну ячейку вправо(R) , влево (L) или остается на месте (E);
4) УУ переходит в другое внутреннее
состояние q i , возможно q i q i .
Состояние q 0 - начальное (МТ начинает
работу),
q z - заключительное состояние.
При переходе в заключительное состояние
машина останавливается.
14. Математическое описание КМТ
где А – внешний алфавит символов,Q – алфавит внутренних состояний
машины,
V – алфавит допустимых движений,
q 0 , q z - начальное и заключительное
состояния,
Q A Q A V
- функция переходов.
15. Способы описания КМТ:
- система команд (программа) ;- функциональная таблица;
- диаграмма состояний (граф переходов).
16.
Система команд (программа) КМТСовокупность команд вида:
q i a j q i a jv,
v V R, L, E ;
называют системой команд или
программой КМТ.
Порядок следования команд в программе
не имеет принципиального значения
17.
Система команд МТ1) начальному шагу алгоритма ставится в
соответствие начальное состояние
2)
соседним
шагам
алгоритма
соответствует переход в смежные
состояния
3) циклы реализуются так, что последнее
действие цикла должно соответствовать
переходу в то состояние, которое
соответствует началу цикла
4) последний шаг алгоритма - переход в
заключительное состояние.
18. Построить МТ, вычисляющую функцию последователь (+1) в унарной системе счисления.
Задача 1.Построить
МТ,
вычисляющую
функцию последователь (+1) в
унарной
системе
счисления.
19.
Унарная (единичная) система счисления -положительная целочисленная система
счисления с основанием, равным 1.
В качестве единственной «цифры»
используется «1» или черточка «/» или «|».
Число x в унарном коде
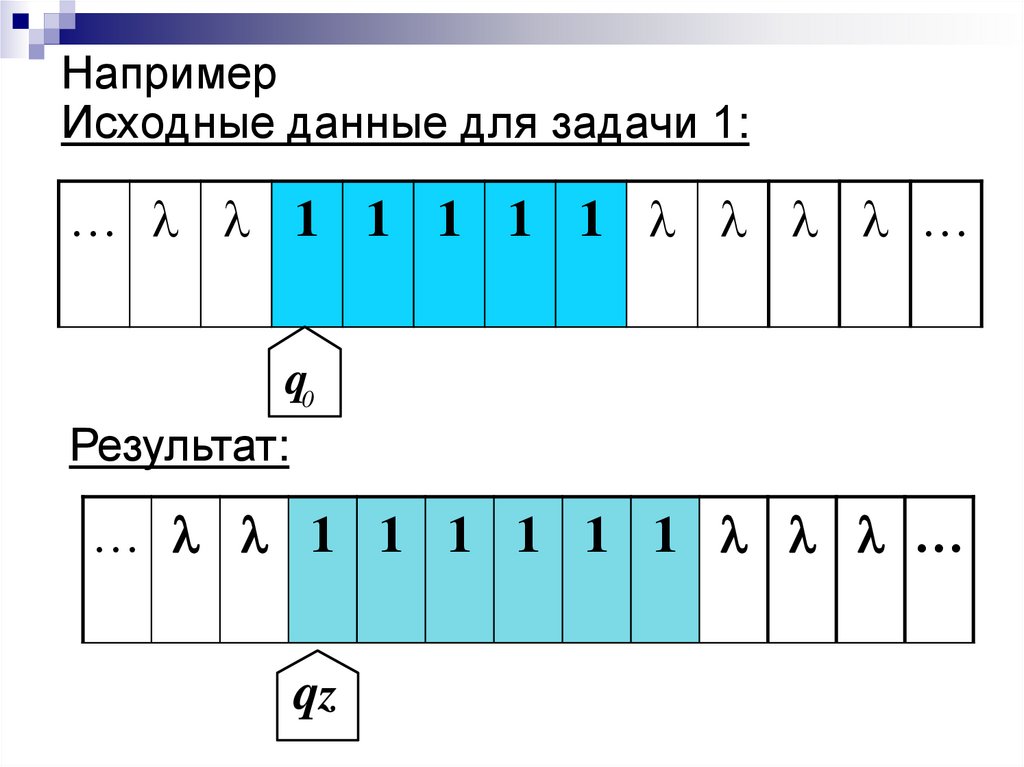
20. Например Исходные данные для задачи 1:
… 1 1 1 1 1 …q0
Результат:
… 1 1 1 1 1 1 …
qz
21. Два варианта решения задачи 1
MT1MT2
22.
Задача 2Построить
МТ,
реализующую
инвертирование числа в двоичной
системе счисления
23.
УУ стоит над первым значащимсимволом слева, в начале рабочей
зоны.
2) На след. такте МТ, не меняя своего
состояния, заменяет символ 0 на 1 и
наоборот и сдвигается вправо на один
символ.
3) После просмотра всей цепочки УУ
обозревает символ, указывающий на
пустую ячейку. В этом случае МТ
переходит в новое состояние и
сдвигается влево на один символ.
1)
24.
4) На последующих тактахУУ не меняя
своего состояния
и обозреваемого
символа, перемещается влево до
пустой ячейки.
Встретив пустую ячейку, МТ
переходит в заключительное состояние
и перемещается вправо на один
символ, переходя в заключительную
стандартную конфигурацию.
5)
25. Функциональная таблица
q i \a ja1
a2
...
aj
q0
q1
...
qi
...
qz
q ia j v
...
an
26.
Каждомусостоянию МТ соответствует
строка в функциональной таблице.
Каждому
символу
из
входного
алфавита столбец.
В клетках таблицы на пересечении
строки
и
столбца
записывается
действие (правая часть команды),
которое выполняется в этом состоянии,
при данном обозреваемом символе.
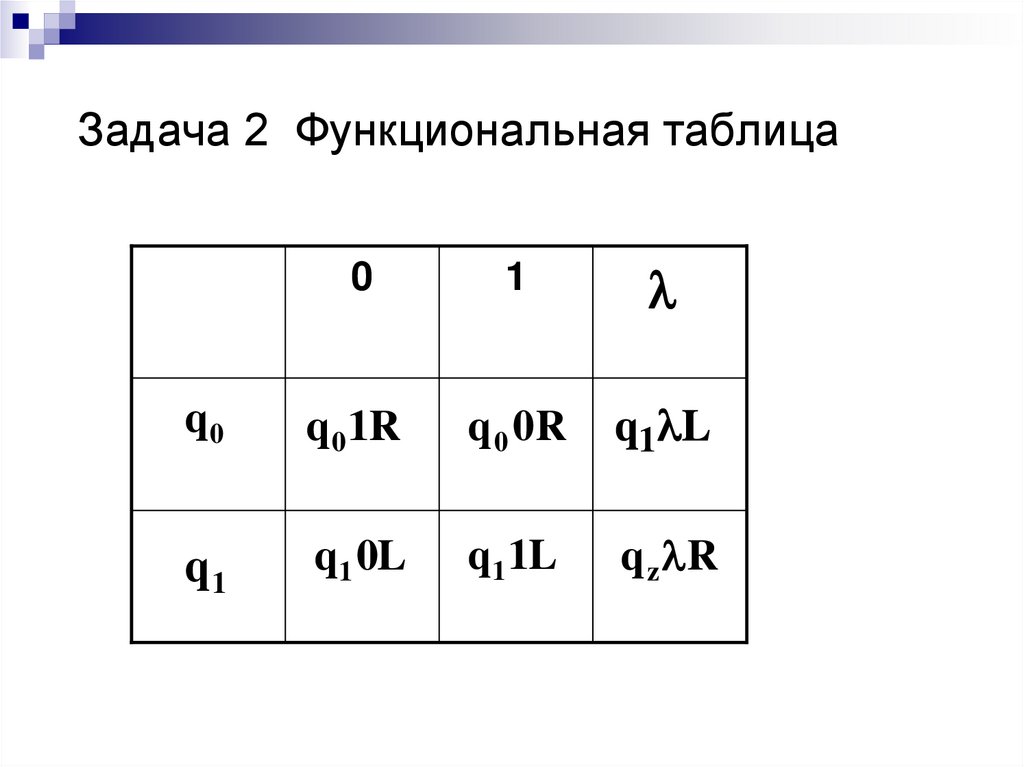
27. Задача 2 Функциональная таблица
01
q0
q 0 1R
q 0 0R
q1
q1 0L
q1 1L
q z R
28. Задача 3 Построить МТ, реализующую сложение двух чисел в унарном коде .
aНачальная конфигурация: q1 1
b
*1 .
Конечная конфигурация:
т.е. сложение фактически сводится к
приписыванию числа b к числу a .
Для этого первая 1 стирается, а *
заменяется на 1.
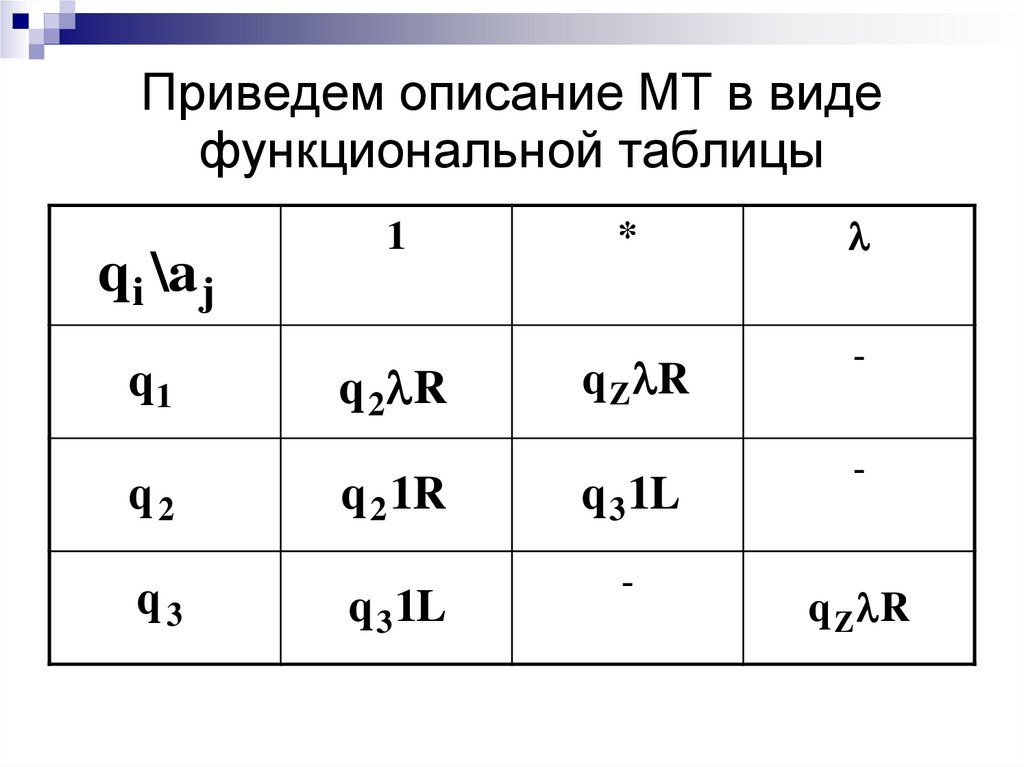
29. Приведем описание МТ в виде функциональной таблицы
q i \a jq1
q2
q3
1
q 2 R
q 2 1R
q 3 1L
*
q Z R
-
q 3 1L
-
-
q Z R
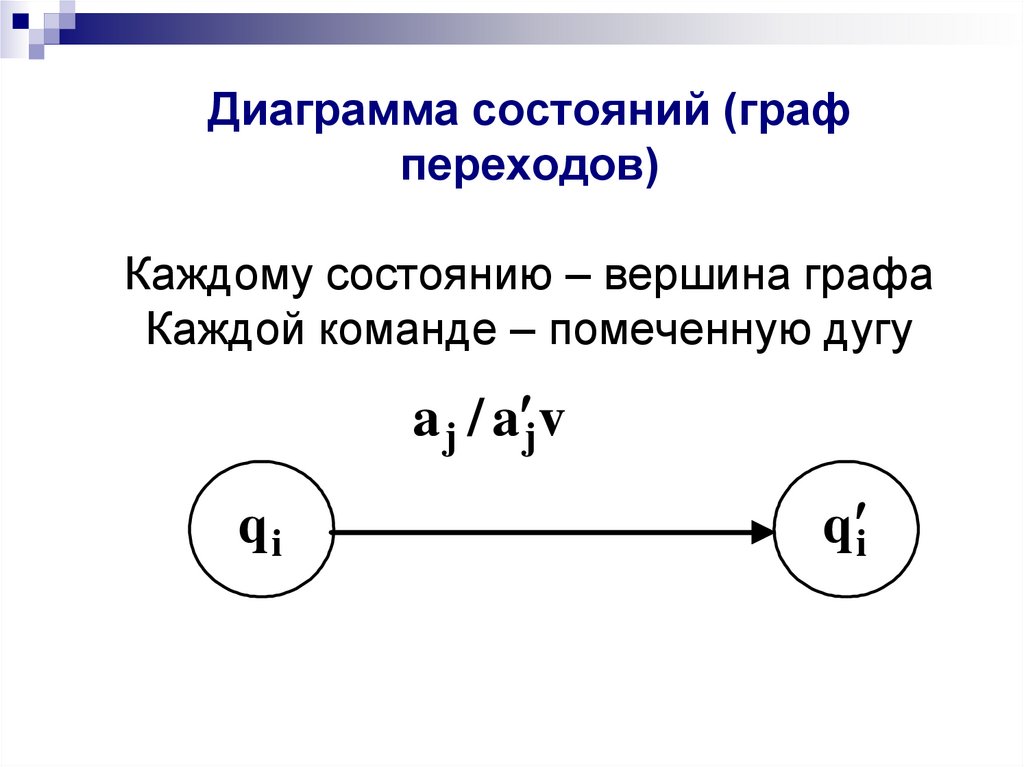
30. Диаграмма состояний (граф переходов) Каждому состоянию – вершина графа Каждой команде – помеченную дугу
a j / a jvqi
q i
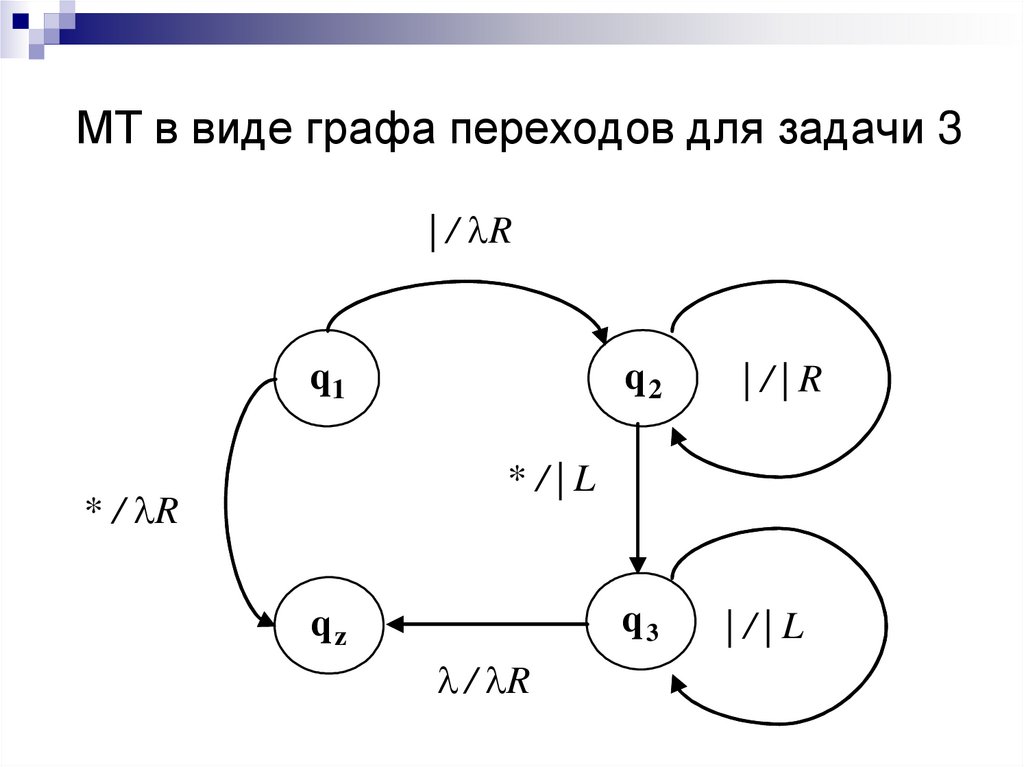
31. МТ в виде графа переходов для задачи 3
| / Rq1
q2
|/ |R
q3
|/ |L
* / |L
* / R
qz
/ R
32. Описание МТ в виде системы команд для задачи 3
q1 1 q 2 Rq1 * q z R
q 2 1 q 2 1R
q 2 * q 3 1L
q 3 1 q 3 1L
q 3 q z R
33.
Полное состояние МТ – конфигурация:состояние рабочей зоны -
распределение букв по ячейкам ленты,
положение рабочей головки и
внутреннее состояние УУ.
Конфигурация в такте t: K t q i a j
где
- подслово слева от обозреваемой
ячейки,
a j - символ в обозреваемой ячейке,
- подслово справа от обозреваемой
ячейки.
34.
K 1 q0 иконечная
называются
стандартными:
Начальная конфигурация
МТ начинает и заканчивает свою
работу в таком положении, когда УУ
обозревает самый левый символ
рабочей зоны ленты.
35.
Функционирование МТ –последовательная смена ее
конфигураций в соответствии с
функцией перехода δ – протокол
работы МТ:
36.
Говорят, что МТ применима к слову α,если она переводит
начальную конфигурацию q 0
за конечное число шагов в некоторую
заключительную конфигурацию q z .
В этом случае МТ вычисляет словарную
функцию f( ).
Если значение f( ) не определено, то МТ
работает бесконечно.
37.
Числовая функция f ( x1 , x 2 ,.., x n )вычислима
по
существует МТ,
конфигурацию
Тьюрингу,
если
которая переводит
q0 1 1
x1
y
x2
.. 1
xn
в конфигурацию q z 1 ,
когда y f ( x1 , x 2 ,.., x n ) ,
или работает бесконечно, когда f ( x1 , x 2 ,.., x n )
не определена.
38.
Тезис Черча для МТ:любая вычислимая в интуитивном смысле
функция вычислима на машине Тьюринга.
Класс функций вычислимых на МТ
совпадает с классом ЧРФ.
39.
Задача 4Построить МТ, вычисляющую функцию
последователь (+1) в двоичной системе
счисления.
q i \a j
0
1
q1
q1 0R
q11R
q 2 L
q2
q 3 1L
q 2 0L
q z 1E
q3
q 3 0L
q 3 1L
q z R
40.
Движение вправо - q1Движение влево -
q2
Добавление 1 -
q3
Протоколы работы МТ для трех тестовых
примеров:
110+1=111
101+1 =110
111+1=1000
41.
42.
101k 1 q1101
k 5 10q 2 1
k 2 1q1 01
k 6 1q 2 00
k 3 10q1 1
k 7 q 3 110
k 4 101q1
k 8 q 3 110 k z
43.
111k 1 q1 111
k 5 11q 2 1
k 2 1q1 11
k 6 1q 2 10
k 3 11q1 1
k 7 q 2 100
k 4 111q1
k 8 q 2 000
k 9 q z 1000





































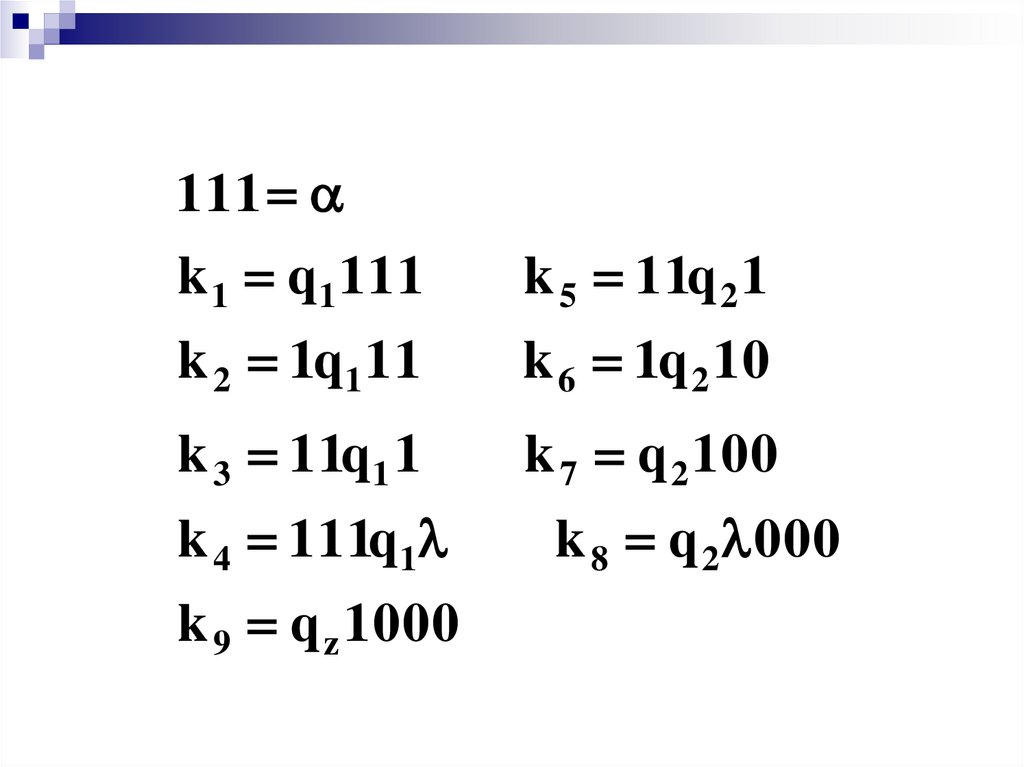
 Информатика
Информатика








