Похожие презентации:
Предел функции
1. Предел функции
Предел функции в точкеОдносторонние пределы
Предел функции при x стремящемся к
бесконечности
Основные теоремы о пределах
Вычисление пределов
Раскрытие неопределенностей
Первый замечательный предел
2.
3. Предел функции
Работайте, работайте, - полное понимание придетпотом.
Даламбер
4. Предел функции в точке
Пусть функция y = f(x) определена в некоторой окрестности точкиx0, кроме, быть может самой точки x0.
Число А называют пределом функции в точке x0 (или при x x0),
если для любого положительного ε найдется такое положительное
число δ, что для всех х из δ – окрестности точки x0 справедливо
неравенство:
f (x) A
0; 0; x : x x0 f ( x ) A
lim f ( x ) A
x x0
5. Предел функции в точке
0; 0; x : x x0 f ( x ) Aε окрестность точки А
y
2
А
0
х0
х
δ окрестность точки x0
Геометрический смысл предела: для всех х из δ – окрестности точки
x0 точки графика функции лежат внутри полосы, шириной 2ε,
ограниченной прямыми: у = А + ε , у = А - ε .
6. Коши Огюстен Луи
Коши Огюстен Луи (1789–1857),французский математик. Работал
в Шербуре инженером,
преподавал в Политехнической
школе, Сорбонне и Коллеж де
Франс.
Работы Коши посвящены
арифметике, теории чисел,
алгебре, математическому
анализу, дифференциальным
уравнениям, механике,
математической физике. Коши
впервые дал четкое
определение пределу,
непрерывности функции,
сходимости ряда и т.д
7. Односторонние пределы
В определении предела функцииlim f ( x ) A
x x0
предполагается, что x стремится к x0 любым способом: оставаясь
меньше, чем x0 (слева от x0), большим, чем x0 (справа от x0), или
колеблясь около точки x0.
Бывают случаи, когда способ приближения аргумента x к x0
существенно влияет на значение предела, поэтому вводят понятия
односторонних пределов.
Число А1 называют пределом функции слева в точке x0, если для
любого ε > 0 найдется такое δ >0, что для всех
x ( x0 ; x0 )
справедливо неравенство:
f ( x ) A1
Предел слева записывают так:
lim f ( x ) A1
x x0 0
8. Односторонние пределы
Число А2 называют пределом функции справа в точке x0, если0; 0; x x0 ; x0 f ( x ) A2
Предел справа записывают так:
Пределы функции слева и
справа называют
односторонними пределами.
y
А2
А1=А2=А
А1
0
lim f ( x ) A2
x x0 0
Очевидно, если существует
х0
х
lim f ( x ) A
x x0
то существуют и оба
односторонних предела,
причем А = А1 = А2
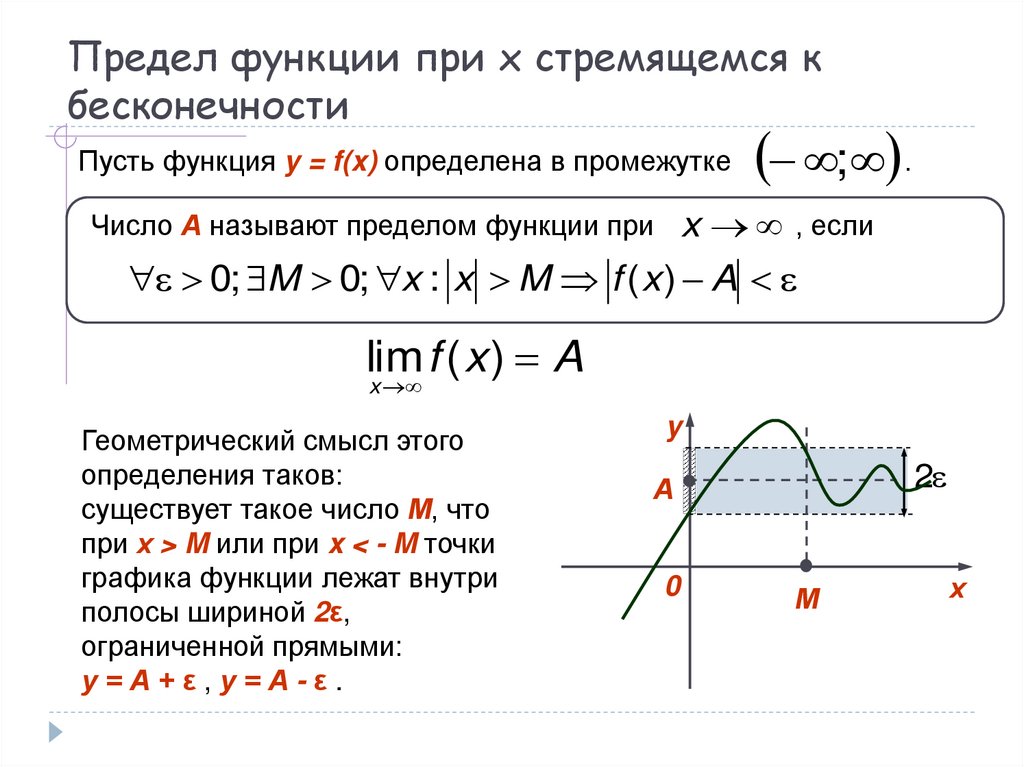
9. Предел функции при x стремящемся к бесконечности
Пусть функция y = f(x) определена в промежутке; .
x , если
Число А называют пределом функции при
0; M 0; x : x M f ( x ) A
lim f ( x ) A
x
Геометрический смысл этого
определения таков:
существует такое число М, что
при х > M или при x < - M точки
графика функции лежат внутри
полосы шириной 2ε,
ограниченной прямыми:
у=А+ε,у=А-ε.
y
2
А
0
М
х
10. Основные теоремы о пределах
Рассмотрим теоремы, которые облегчают нахождение пределовфункций.
Формулировка теорем, когда x x0 или x аналогичны,
поэтому будем пользоваться обозначением: lim f ( x ).
Предел суммы (разности) двух функций равен сумме (разности)
пределов:
lim f1( x ) f2 ( x ) lim f1( x ) lim f2 ( x )
Предел произведения двух функций равен произведению
пределов:
lim f1( x ) f2 ( x ) limf1( x ) limf2 ( x )
Постоянный множитель можно выносить за знак предела:
lim C f ( x ) C limf ( x )
11. Основные теоремы о пределах
Предел дроби равен пределу числителя, деленному на пределзнаменателя, если предел знаменателя не равен нулю:
f1( x ) lim f1( x )
lim
f2 ( x ) lim f2 ( x )
lim f ( x ) 0
2
Предел степени с натуральным показателем равен той же
степени предела:
lim f ( x ) lim f ( x )
n
n
Предел показательно – степенной функции:
lim f ( x )
g(x)
lim f ( x )
lim g ( x )
12. Основные теоремы о пределах
Если между соответствующими значениями трех функцийu u( x );
z z( x ); v v ( x )
выполняются неравенства: u z v, при этом:
lim u( x ) lim v ( x ) A тогда: lim z( x ) A
Если функция f(x) монотонна и ограничена при x < x0 или при
x > x0, то существует соответственно ее левый предел:
lim f ( x ) A1
x x0 0
или ее правый предел:
lim f ( x ) A2
x x0 0
13. Бесконечно малые функции
Функция f(x) называется бесконечно малой при х->x0, еслиlim f x 0
x x0
.
Обозначение: α, β, γ и т.д.
Функция f(x) называется бесконечно большой при х->x0, если
lim f x
x x0
Если ( x )есть б.м. , то
Если
( xесть
)
б.б., то
Связь между1 б.м. и б.б.
( x)
б.б.
1
б.м.
( x)
14.
Свойства бесконечно малых.Теорема 1. Если функция f(x) имеет предел при х->x0,
равный А, то она представима в виде
f(x) = А + α(х) , где α(х) – б.м.ф.
Справедливо и обратное: если функция f(x) представима равенством f(x)
= А + α(х) при х->x0, то её предел равен А.
Теорема 2. Алгебраическая сумма конечного числа бесконечно малых в
точке функций есть бесконечно малая функция
15.
Теорема 3. Произведение ограниченной при функции набесконечно малую есть бесконечно малая функция.
Следствие 1. Произведение постоянной величины на
бесконечно малую есть функция бесконечно малая.
Следствие 2. Произведение конечного числа бесконечно
малых функций есть функция бесконечно малая
16.
17. Вычисление пределов
Вычисление предела:lim f ( x ) A
x x
0
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому
числу.
3x 1
3 1 1
lim
2
2
2
x 1
x
1
Если при подстановки предельного
значения x0 в функцию f(x) получаются
выражения вида:
то предел будет равен:
C
0
C
0
18. Вычисление пределов
Часто при подстановке предельного значения x0 в функцию f(x)получаются выражения следующих видов:
0
;
0
; 0 ; 1 ; 00 ; 0 ; 0 ;
Эти выражения называются неопределенности, а вычисление
пределов в этом случае называется раскрытие
неопределенности.
19. Раскрытие неопределенностей
Раскрытие неопределенности0
0
x 2 14 x 32
0
x
2
x
16
lim 2
lim
x 2
x 2
x 6x 8
0
x 2 x 4
x 16 18
lim
9
x 2
x 4
2
Если f(x) – дробно –
рациональная
x 1 1 x 1 1
0
x 1 1 функция,
наlim Если f(x) – иррациональная
lim необходимо разложить
x 0
0
множители
числитель
иx 0 дробь, x
x
x 1 умножить
1
необходимо
знаменатель дроби
числитель и знаменатель
x 1 1
1дроби на выражение,
1
lim
lim
числителю.
x 0
x 0
сопряженное
x x 1 1
x 1 1 2
20. Раскрытие неопределенностей
Раскрытие неопределенности2x 2 3 x 1
2 2
2
2x 2 3 x 1
x
x
x
lim
lim
2
x
x 4 x 2
4 x 2x 5
2x 5
2 2
2
x
x
x
3 1
2 2
C
2 0 0 1
x
x
lim
f(x) – дробно
0 –
Если
x
2 5рациональная
4 0 0 2
функция
или
4 2
x x иррациональная дробь
необходимо разделить
числитель и знаменатель
дроби на x в старшей степени
21. Раскрытие неопределенностей
Раскрытие неопределенностиlim x 2 1 x 2 1
x
x 1 x 1 x 1 x 1
lim
x 1 x 1
2
x
lim
x
2
2
2
2
2
Умножим и разделим
2
( x 1) ( x функцию
1)
на
сопряженное
lim
x
2
2
выражение.
x2 1
2
2
x 1 x 1
2
0
x2 1
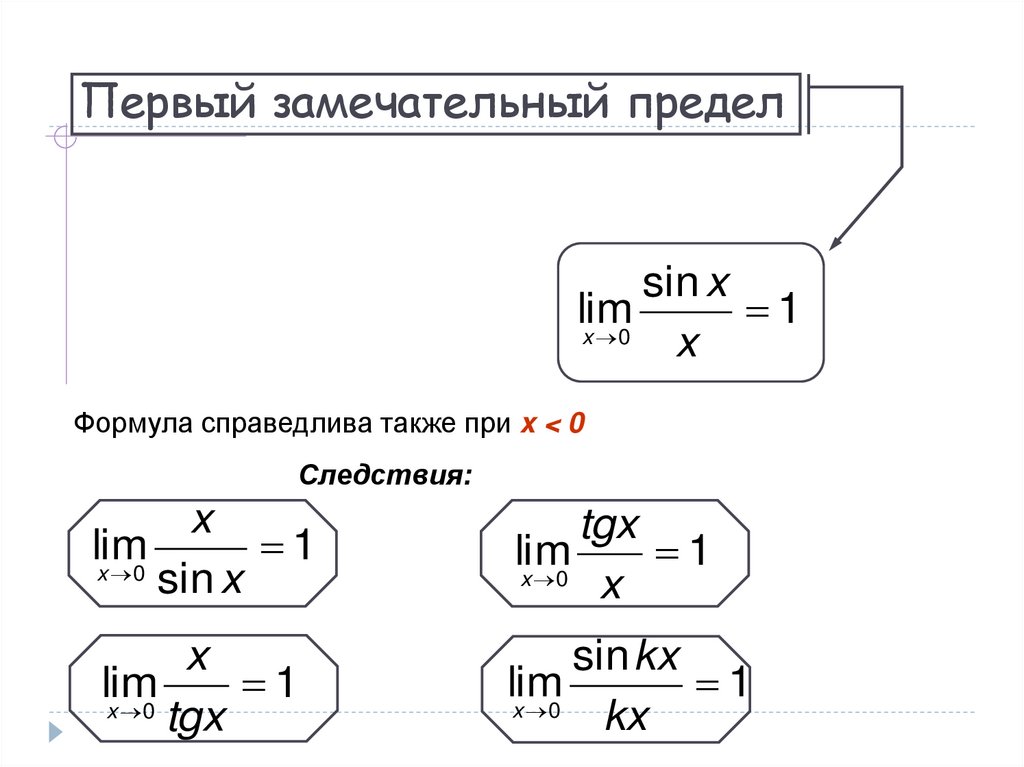
22. Первый замечательный предел
sin xlim
1
x 0
x
Формула справедлива также при x < 0
Следствия:
x
lim
1
x 0
sin x
tgx
lim
1
x 0
x
x
lim
1
x 0
tgx
sin kx
lim
1
x 0
kx
23. Первый замечательный предел
02 sin 2 x
1 cos 4 x
sin 2x
lim
lim
2 lim
2
2
x 0
x 0
x
0
0
x
x
x
2
2
sin 2x 2 lim 2 sin 2x
x 0
2 lim
2x
x 0 x
2
2
sin 2x
2
2 2 lim
2 2 1 8
x 0
2x
2
24. Второй замечательный предел
Вторым замечательным пределом называется равенство:Следствия:
2.7182818284
1
x
1
lim 1 e
x
x
lim 1 x x e
x 0
kx
1
lim 1
e
x
kx
Второй замечательный предел применяется для раскрытия
неопределенности 1 .
Другие полезные формулы:
(1 x ) 1
lim
m
x 0
x
m
ln( 1 x )
lim
1
x 0
x
ax 1
lim
ln a
x 0
x
25. Второй замечательный предел
x 3x 1 4
lim
lim
x
x
x 1
x 1
x 3
4
1
x 1 y
1
lim 1
y
y
x 3
4
lim 1
x
x 1
x 4y 1; x ; y
4 y 1 3
4y
1
1
lim 1 1
y
y
y
4
4
4
1
1
lim 1 lim 1 e 4 14 e 4
y
y y
y
y
x 3






















 Математика
Математика








