Похожие презентации:
Геометрические тела с вырезом
1.
Построить три проекциипирамиды SABC с вырезом .
2.
Так как вырез пирамиды призматическийи каждая грань призматического выреза
пересекает пирамиду по плоским
многоугольникам , то построение этих
многоугольников сводится к задаче на
принадлежность точек поверхности
пирамиды .
3.
sa
b
a
b
c c
4.
xa
s
z
b
c
c c
s
y
a
b
1) Построим третью проекцию пирамиды .
a
b
2) Отмечаем точки выреза .
На ребрах пирамиды по одной
точке
5.
65
1
s
2
a
b
s
3 4
c
c c
a
b
4-х угольн.,точки
1,2,3,4
a
b
4-x угольн.,точки
6,5,3,4
6.
3) Точки 1,6 принадлежат ребру SA.Точки 2,5 принадлежат ребру SB.
Точка 3 принадлежит прямой 2-3 / / BC .
Точка 4 принадлежит прямой 1-4 / /AC .
4) Находим горизонтальные проекции точек,
а затем их профильные проекции
7.
s6
*
5
1
a
a
2
6
1
b
6
3 4 4
4
* 3
5
b 2
c
c c
3
s
5
1
2
a
b
4-х угольн.,точки
1,2,3,4
4-x угольн.,точки
6,5,3,4
8.
*6
a
1
b
4
* 3
5
2
c c
9.
S6
5
4
1
3
А
2
В
С
10.
Построить три проекции призмыс вырезом .
11.
zx
a
c c c
b
a
b
a
y
b
1) Построим третью проек цию .
2) Отмечаем точки выреза.
На ребрах призмы по одной
точке .
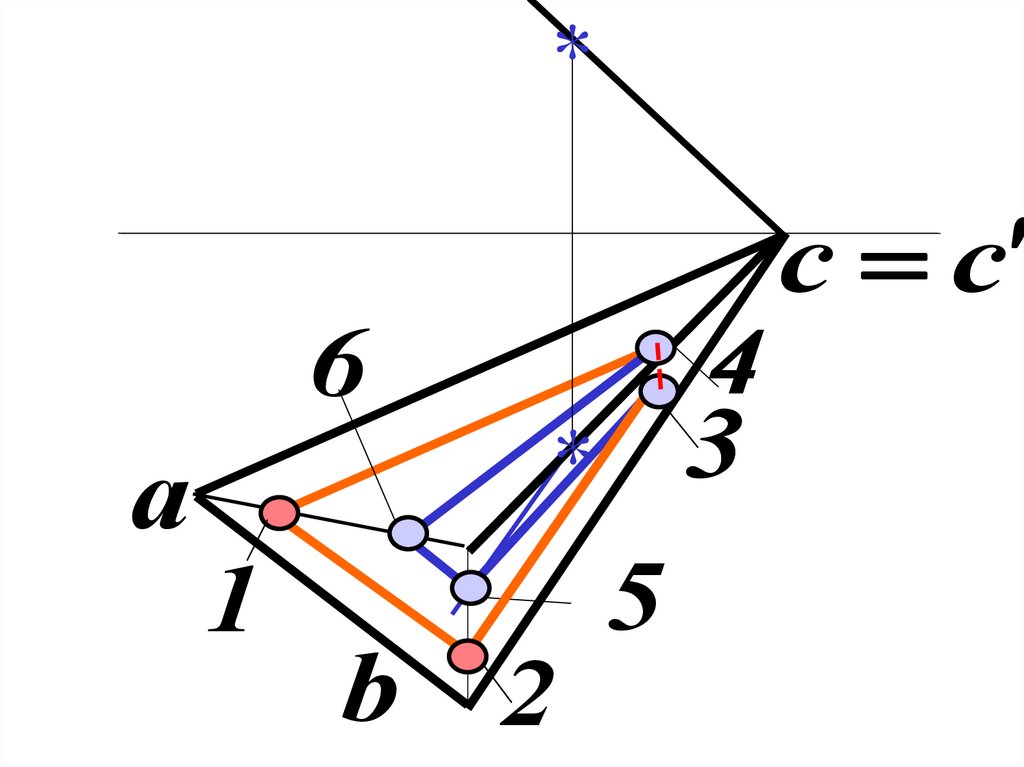
12.
5 67
1
a
a
2
b
3 4
c c c
a
b
4-х угольник , точки 1,2,3,4
5-ти угольник ,
точки 3,4,7,6,5
Находим горизонтальную и проb фильную проекции точек .
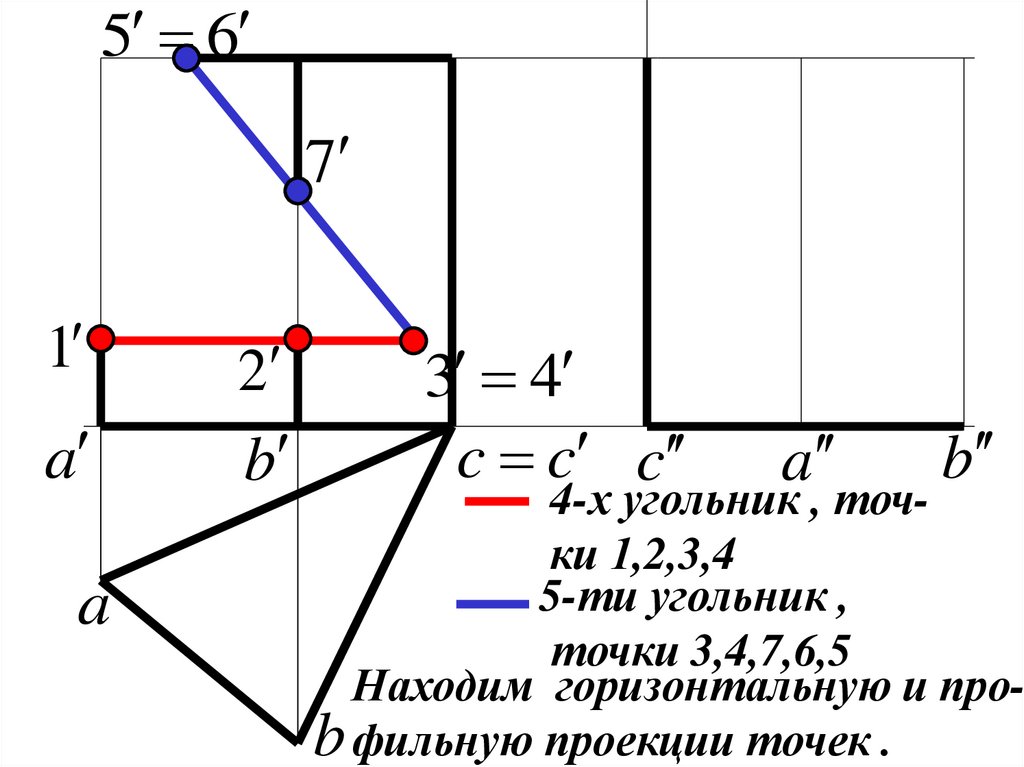
13.
55 6
7
1
2
b
a
5
1 a
6
6
7
3
3 4
4 1
2
c c c a
b
3
Точка 1 ребру А .
4
Точки 2 ,7 ребру В
Точки 5,6 принадлежат верхнему основанию .
b 2 7
14.
Построить три проекциицилиндра с вырезом .
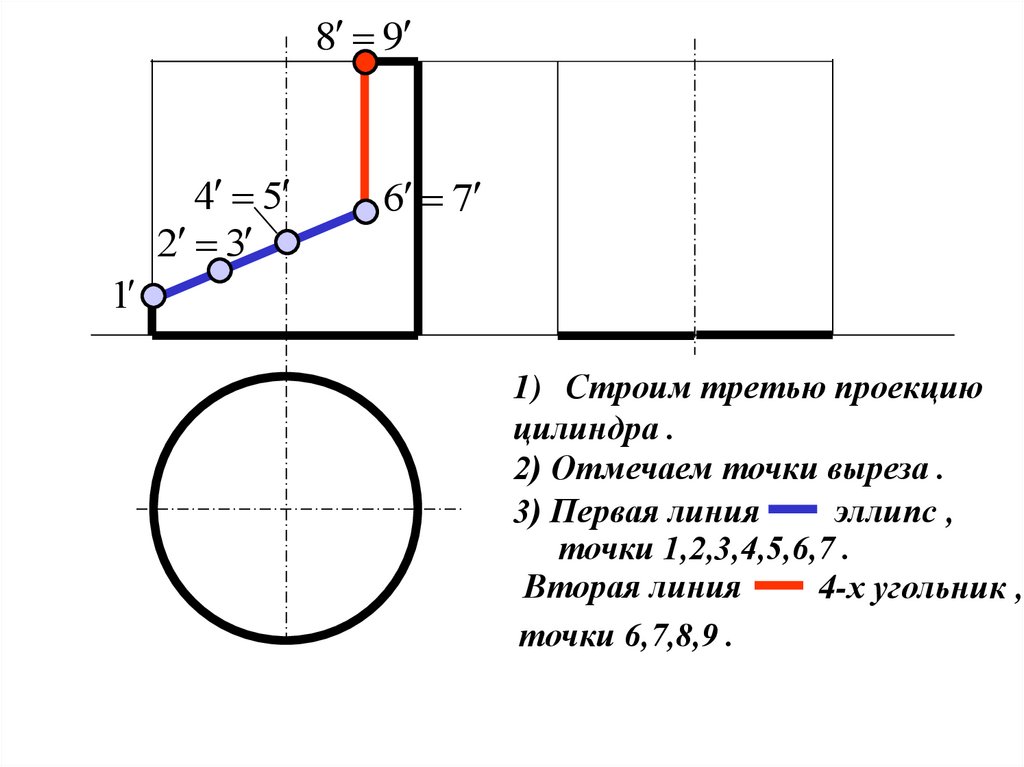
15.
8 94 5
2 3
6 7
1
1) Строим третью проекцию
цилиндра .
2) Отмечаем точки выреза .
3) Первая линия
эллипс ,
точки 1,2,3,4,5,6,7 .
Вторая линия
4-х угольник ,
точки 6,7,8,9 .
16.
8 94 5
2 3
5
3
5
6 8
1
4
7 9
1
2
4
4) Горизонтальная проекция
точек принадлежит горизонтальному очерку цилиндра .
5)
2
7
6
6 7
1
3
9
8
4,5 профильному очерку
17.
Построить три проекции конусас вырезом .
18.
8r
6 7
1
2 3 4 5
1) Строим третью проекцию
конуса .
2) Отмечаем точки выреза .
3) Первая линия
окруж ность – r (параллельна основанию)
и ограничена точками 1,2,3,4,5 .
гипербола
Вторая линия
( параллельна двум образующим
конуса ) и ограничена точки 4,6,8,7.5 .
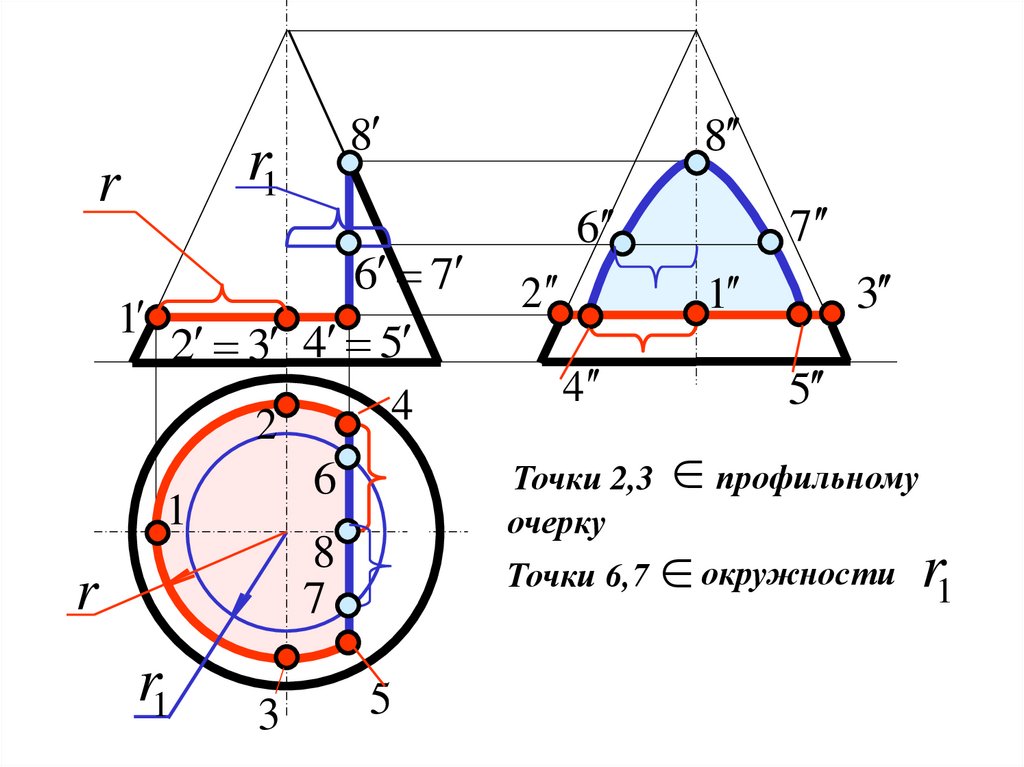
19.
8r1
r
6 7
1
2 3 4 5
4
2
8
7
r
r1
3
2
3
1
4
Точки 6,7
5
7
6
Точки 2,3
очерку
6
1
8
5
профильному
окружности r1
20.
Построить три проекции сферыс вырезом .
21.
r1
2 3
4 5
6 7 8 9
10
1) Построить три проекции сферы .
2) Отмечаем точки выреза сферы ,
на очерке сферы по одной точке , в
остальных случаях по две точки .
окружность r,
3) Первая линия
которая параллельна профильной
плоскости проекций и ограничена
точками 1,2,3,4,5 .
окружность R ,
Вторая линия
ограниченная точками 4,6,8,10,9,7,5 и
проекция которой – эллипс .
22.
1r
1
2 3
4 5
6 7 8 9
2
4 6
10
8
10
1
5 7
3
экватор
r
9
6
8
2
4
3
10
5
7
9
r.
1) Провели окружность радиуса
Точки 2,3 Экватору .
2) На линиях связи для точек 6,7 откладываем от осей отрезки равные Rрадиусу окружности сечения .
3) Точки 8,9 профильному очерку
23.
r1
2 3
6 7 4 5
10
8 9
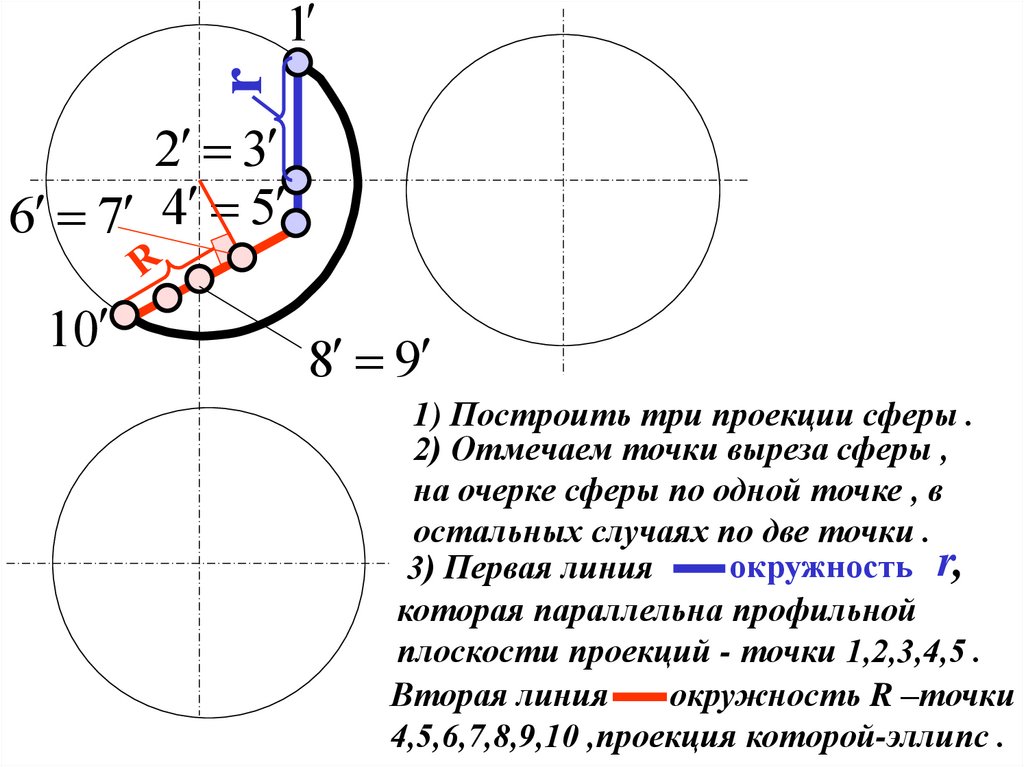
1) Построить три проекции сферы .
2) Отмечаем точки выреза сферы ,
на очерке сферы по одной точке , в
остальных случаях по две точки .
окружность r,
3) Первая линия
которая параллельна профильной
плоскости проекций - точки 1,2,3,4,5 .
Вторая линия
окружность R –точки
4,5,6,7,8,9,10 ,проекция которой-эллипс .
24.
1r
r
1
2 3
6 7 4 5
10
10
экватор
2
4
3
5
7
9
6
8
8 9
10
6
1) Провели окружность радиуса r.
2
8
Точки 2,3 экватору .
4
2) На линиях связи для точек 6,7 от1 кладываем от осей сферы отрезки
равные R-радиусу окружности сечения
. -
5
97 3
.
3) Точки 8,9 профильному очерку
4) Для точного построения эллипса
необходимы промежуточные точки .



















 Математика
Математика Инженерная графика
Инженерная графика








