Похожие презентации:
Показатели вариации. Тема 6
1. Показатели вариации
«Всякая вещь есть формапроявления
беспредельного
разнообразия»
Козьма Прутков,
Плоды раздумья
2.
План лекции1. Абсолютные показатели вариации
2. Относительные показатели вариации
3.Меры
вариации для
сгруппированных данных
4.Правило сложения дисперсий
5. Вариация альтернативного признака
3.
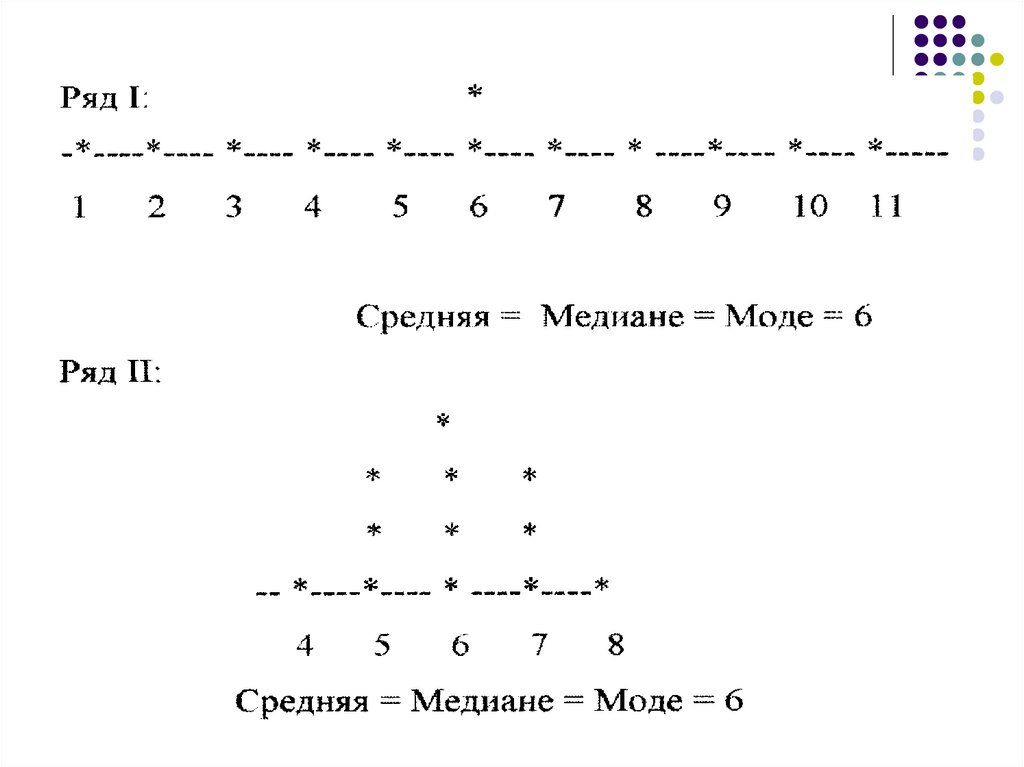
Ряд I: 1, 2, 3, 4, 5, 6, 6, 7, 8, 9, 10, 11Ряд II:
4, 5, 5, 5,6, 6, 6, 6, 7, 7, 7, 8
x 6, Me 6, Mo 6, n 12
x 6, Me 6, Mo 6, n 12
4.
5.
Интерквартильный размах –разница между первым и
третьим квартилями. Чем
больше величина интерквартильного
размаха, тем больше рассеяние
признака. Интерквартильный размах
в ряду I равен 5.5, интерквартильный
размах в ряду II равен 2.
6.
Размах вариации - разность междунаибольшим и наименьшим
значениями признака
R xmax xmin
7.
x xn
Сумма отклонений всех вариантов
от их средней арифметической,
согласно
свойству
средней
арифметической, всегда равна нулю.
8.
LL
x
x
n
x x f
f
9.
x x2
2
n
2
k
2
x x f
i 1
i
k
f
i 1
i
i
10.
Дисперсия вариационного ряда естьсредняя арифметическая квадрата
отклонения (средний квадрат
отклонения) значений признаков ряда
от их средней арифметической.
11.
Среднее квадратическое (стандартное)отклонение вариационного ряда есть
арифметическое значение корня
квадратного из дисперсии.
2
12.
Среднее квадратическое(стандартное) отклонение
вариационного ряда есть
арифметическое значение корня
квадратного из дисперсии.
2
13. Показатели относительного рассеяния
Расчет показателей мерыотносительного рассеяния
осуществляют как отношение
абсолютного показателя вариации
признака к средней арифметической,
умножаемое на 100%.
14.
Коэффициент осцилляции отражаетотносительную колеблемость крайних
значений признака вокруг средней:
R
К 0 100%
х
15.
Относительное линейное отклонениехарактеризует долю усредненного
значения признака абсолютных
отклонений от средней величины:
L
K L 100
x
16.
Коэффициент вариации являетсянаиболее распространенным
показателем колеблемости,
используемым для оценки типичности
средних величин:
V
x
17.
Предположим, что стандартное отклонение ввыборке валютных счетов в банке «А» и
банке «В» равно $20. Данные по банку «А»
содержат информацию о счетах, сумма
которых находится в пределах $60. В банке
«В» данные содержат информацию
относительно счетов, сумма которых
достигает $1 миллион и больше. В первом
случае стандартное отклонение в 20 единиц
очень велико относительно сумм счетов. Для
суммы порядка $1 миллиона – что значит
вариация плюс-минус $20 относительно
среднего?
18.
Сравнивая эти два случая, можно сказать, чтотакая абсолютная мера рассеяния как
стандартное отклонение не передает
существенной информации при сравнении
вариационных рядов. Коэффициент вариации
создан специально как относительная мера
вариации.
Чем меньше значение коэффициента
вариации, тем однороднее совокупность по
изучаемому признаку и типичнее средняя. В
статистике совокупности, имеющие
коэффициент вариации больше 30-35 %,
принято считать неоднородными.
19.
Однако у такого способа оценки вариацииесть и существенный недостаток. Например,
исходная совокупность рабочих, имеющих
средний стаж 15 лет, со средним
квадратическим отклонением = 10 лет,
«состарилась» еще на 15 лет. Теперь = 30 лет,
а среднеквадратическое отклонение попрежнему равно 10. Совокупность, ранее
бывшая неоднородной (10/15 100 = 66,7%),
со временем оказывается, таким образом,
вполне однородной (10/30 100 = 33,3 %).
20. Меры вариации для сгруппированных данных. Правило сложения дисперсий
Вариация признаков, как правило, обусловленавлиянием
различных
факторов.
Если
совокупность разбить на группы по факторному
признаку, то это окажет определенное влияние
на значение вариации признака в группах.
Выявить долю вариации, определяемую теми или
иными факторами, можно разделяя всю
совокупность на группы по фактору, влияние
которого исследуется.
21.
Для этих целей используются показателивариации для сгруппированных данных. В
этом случае выделяют три вида дисперсий:
Общую дисперсию; внутригрупповую
дисперсию, межгрупповую дисперсию.
Общая дисперсия измеряет вариацию признака
во всей совокупности под влиянием всех
факторов. Внутригрупповая дисперсия
измеряет вариацию признака внутри группы, а
межгрупповая дисперсия измеряет вариацию
групповых средних относительно общей
средней.
22.
Значениепризнака x
Число
единиц
в j -й
группе
Итого
1
2
…
m
x1
f1
s1
…
t1
f1 s1 ... t1 n1
x2
f2
s2
…
t2
f 2 s2 ... t 2 n2
…
…
…
…
…
xk
fk
sk
…
tk
Итого
N1
N2
…
Nm
…
f k sk ... t k nk
N
23. Вычислим m частных средних
x1k
xi f i
i 1
N1
24.
kx2
x s
i 1
i i
N2
…
k
xm
xt
i 1
i i
Nm
.
25.
На основе частных среднихx1 , x2 ,..., xm
определяем общую среднюю
xобщ.
m
xjN j
j 1
N
, где
m
k
N N j ni
j 1
i 1
26. Общая дисперсия отражает вариацию признака за счет всех условий, действующих в совокупности
2общ.
k
2
xi xобщ. ni
i 1
N
27. Межгрупповая дисперсия отражает вариацию между группами за счет фактора, положенного в основу группировки
xx
N
m
2
j 1
2
j
N
j
28. Частная групповая дисперсия отражает вариацию внутри каждой группы
k2
xi x1 f i
2 i 1
1
N1
29.
k2
xi x2 si
2 i 1
2
N2
…….
k
2
xi xm ti
2 i 1
m
Nm
30.
В общем виде частная дисперсия:x
x
N
k
2
j
i 1
2
i
j
Nj
где Nij- частоты для значений xi, в
каждой j-группе, j=1,…,m.
ij
31. Внутригрупповая дисперсия - средняя арифметическая из групповых дисперсий
m2
N
j
j 1
2
j
N
32.
Общая дисперсия равна сумме межгрупповойдисперсии и средней из внутригрупповых
дисперсий
2
2
2
Суть
правила:
общая
дисперсия,
возникающая
под
воздействием
всех
факторов,
формируется
из
дисперсии,
возникающей за счет фактора группировки и
дисперсии, возникающей под воздействием
всех прочих факторов.
33.
С помощью правила сложения дисперсийоценивается удельный вес факторов,
лежащих в основе группировки, во всей
совокупности факторов, воздействующих
на результативный признак. Для этого
применяется коэффициент детерминации
2
2
2
34. Эмпирическое корреляционное отношение
22
35.
Показатель принимает значения в интервале[0, 1] и и характеризует взаимосвязь между
изучаемым признаком и признаком, положенным в
основу группировки. Если связь между признаками
отсутствует, то = 0. В этом случае дисперсия
групповых средних равна нулю ( 2 = 0), то есть все
групповые средние равны между собой и
межгрупповой вариации нет. Если связь
функциональная, то =1. В этом случае дисперсия
групповых средних равна общей дисперсии ( 2 =
2), то есть внутригрупповая дисперсия
отсутствует. Это означает, что группировочный
признак полностью определяет вариацию
изучаемого признака, а влияние прочих факторных
36.
Промежуточные значения оцениваются постепени их близости к граничным
Качественная оценка связи между признаками
(шкала Чеддока)
0
0-0,2
0,2-0,3
0,3-0,5
Связь
Отсутствует
Очень слабая
Слабая
Умеренная
0,5-0,7
0,7-0,9
0,9-0,99
1
Связь
Заметная
Тесная
Весьма тесная
Функциональная
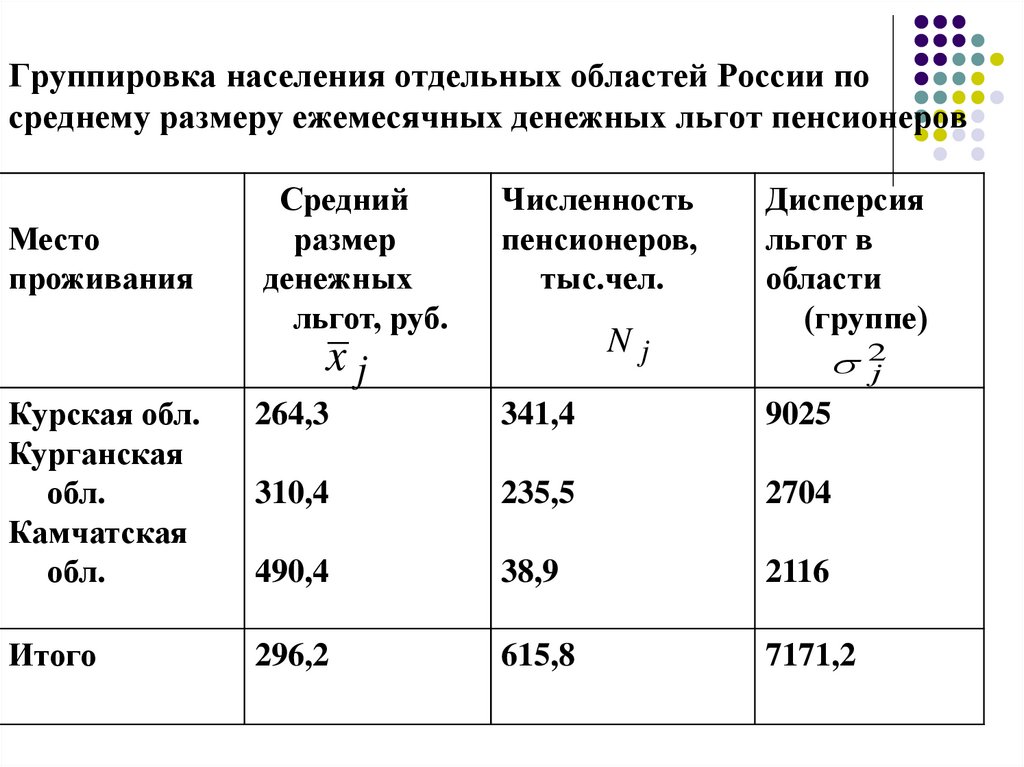
37. Группировка населения отдельных областей России по среднему размеру ежемесячных денежных льгот пенсионеров
Местопроживания
Средний
размер
денежных
льгот, руб.
Численность
пенсионеров,
тыс.чел.
Nj
xj
Дисперсия
льгот в
области
(группе)
2j
Курская обл.
Курганская
обл.
Камчатская
обл.
264,3
341,4
9025
310,4
235,5
2704
490,4
38,9
2116
Итого
296,2
615,8
7171,2
38.
Найдем средний размер льгот (руб.) по тремобластям в целом:
x N 264,3 341,4 310,4 235,5 490,4 38,9
x
296,2
615,8
N
j
j
j
j
j
39.
Вариация льгот по отдельным областям,обусловленная различием в месте проживания
пенсионеров, характеризуется межгрупповой
дисперсией:
x x N 264,3 296,2 341,4 310,4 296,2 235,5
m
2
j 1
2
j
j
2
N
615,8
490,4 296,2 38,9
3023,6 руб.2
2
615,8
2
40.
Средняя из групповых дисперсий дает обобщающуюхарактеристику случайной вариации, обусловленную
отдельными факторами, кроме места проживания
пенсионеров (например, характером занятости,
стажем работы и т.п.):
9025 341,4 2704 235,5 2116 38,9
2
6171,2 руб.
615,8
2
41.
Вариация льгот в изучаемых областяхРоссии, обусловленная влиянием всех
факторов, вместе взятых, определяется
общей дисперсией:
2976,1 6171,2 9147 ,3
2
2
2
42.
22
2
общ.
2976 ,1
0,325
9147 ,3
43.
Полученный коэффициент детерминациипоказывает, что дисперсия льгот зависит от
места проживания пенсионеров на 32,5 %.
Остальные 67,5% определяются другими
неучтенными факторами.
0,325 0,57
2
Полученное значение эмпирического
корреляционного отношения позволяет
утверждать, что существует заметная связь
между местом проживания пенсионеров и
размером льгот.
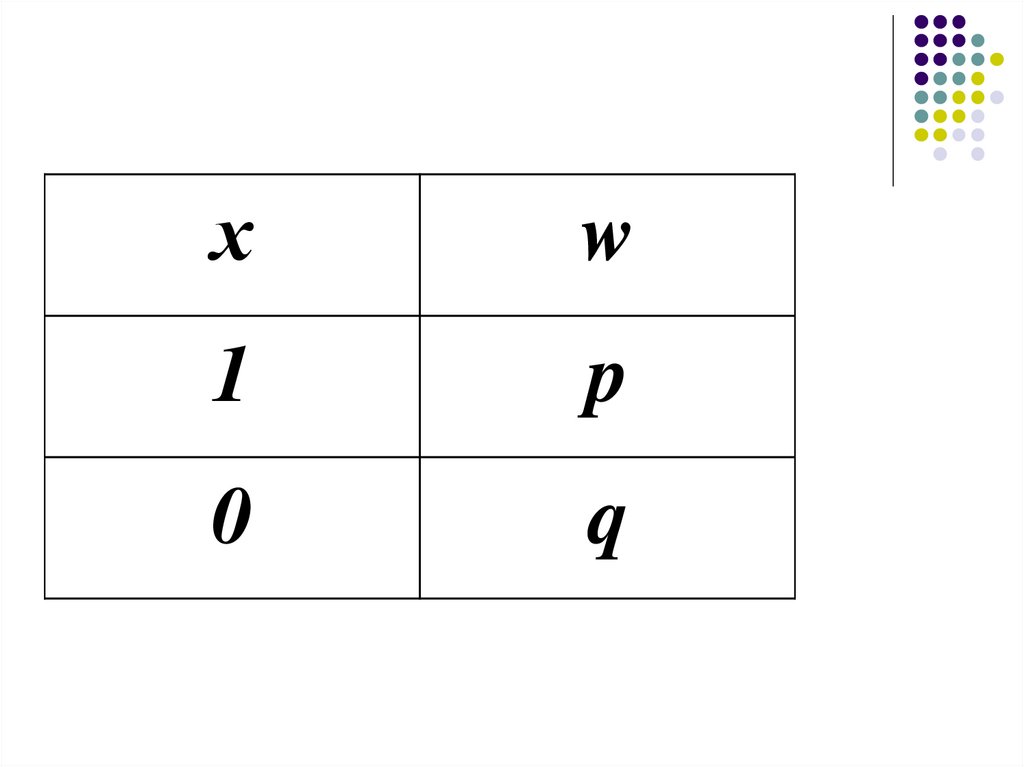
44. Вариация альтернативного признака
При статистическом выраженииколеблемости альтернативных признаков
наличие изучаемого признака
обозначается 1, а его отсутствие – 0. Доля
вариантов, обладающих изучаемым
признаком обозначается р, а доля
вариантов, не обладающих признаком q.
Следовательно, р + q=1.
45.
хw
1
p
0
q
46.
x f 1 p 0 qx
p
p q
f
i
i
i
i
i
47.
( x x ) f (1 p) p (0 p) qq p p q pq( p q) pq
p q
f
2
i
2
p
i
2
2
2
i
i
i
2
48.
Если значения 1 и 0 встречаются одинаковочасто, то дисперсия достигает своего
максимума
Пример. На 10000 населения приходится
4000 мужчин и 6000 женщин. Определить
среднее квадратическое отклонение по полу.
Решение. Доля мужчин в населении
p=4000/10000=0,4; доля женщин
q=6000/10000=0,6. Тогда дисперсия
pq 0,4 0,6 0,24
2
p
а среднее квадратическое отклонение
p 0, 24 0, 49
2
p
49.
Внутригрупповая дисперсия доли2
pi pi (1 pi )
Средняя из внутригрупповых дисперсий
2
pi
pi (1 pi )ni p (1 p )
i
i
ni
50.
межгрупповая дисперсия(
p
p
)
n
2
i
i
pi
ni
2
51.
где ni – численность единиц в отдельныхгруппах;
p – доля изучаемого признака во всей
совокупности, которая определяется по
формуле:
pi ni
p
ni
52.
Общая дисперсияp(1 p)
2
p
Правило сложения дисперсии доли признака
2
2
2
p pi pi
53.
ЦехУдельный
Численность
вес основных всех рабочих
рабочих в % (чел.)
(pi)
1
80
100
2
75
200
3
90
150
Итого
-
450
54.
Определим долю рабочих в целом пофирме:
0,80 100 0, 75 200 0,90 150 365
p
450
450
0,81
55.
Общая дисперсия долиосновных рабочих по всей
фирме в целом будет равна:
2
р 0,81 1 0,81 0,154
56.
Внутрицеховые дисперсии:2
p1 0,8 0,2 0,16;
2
p 2 0,75 0,25 0,19;
2
p3 0,9 0,1 0,09.
57.
Средняя из внутрицеховых дисперсий:0,16 100 0,19 200 0,09 150 675
2
pi
0,15
450
450
Межгрупповая дисперсия:
0,8 0,81 100 0,75 0,81 200 0,9 0,81 150
2
2
pi
365
0,004
450
2
450
2






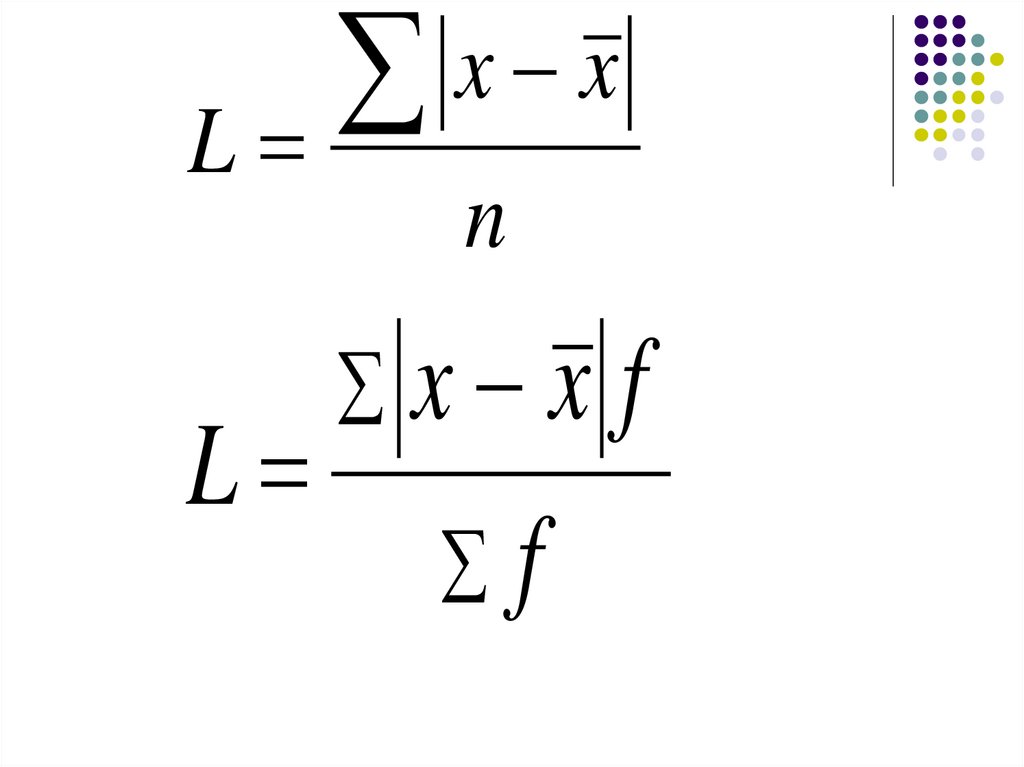
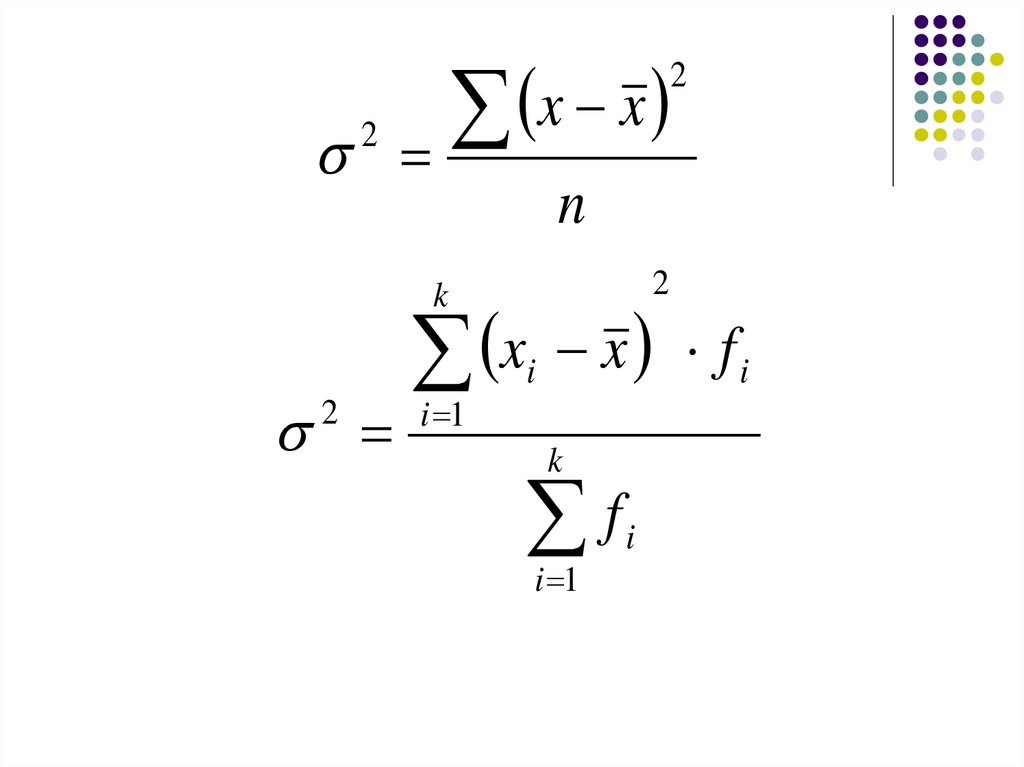













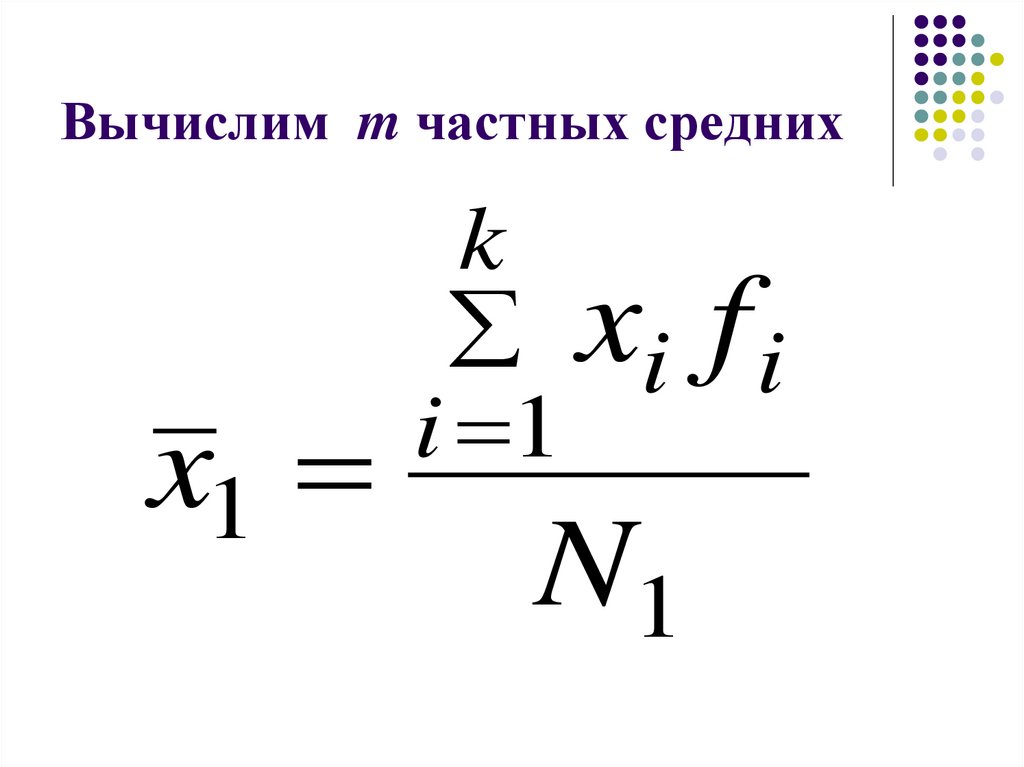





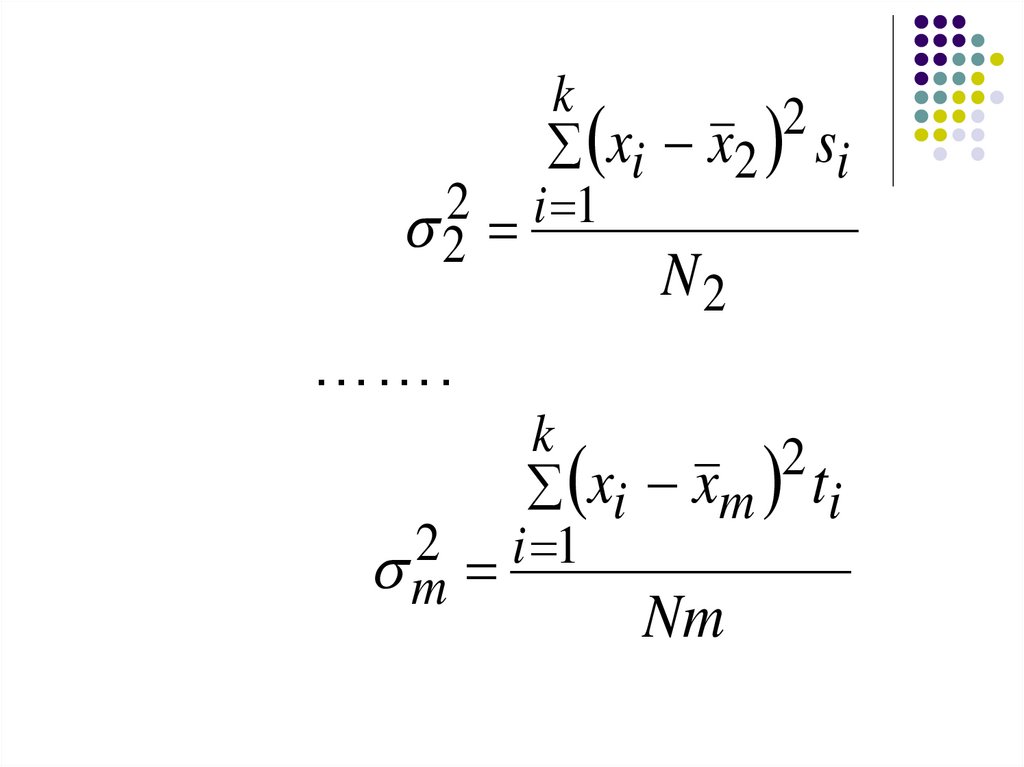











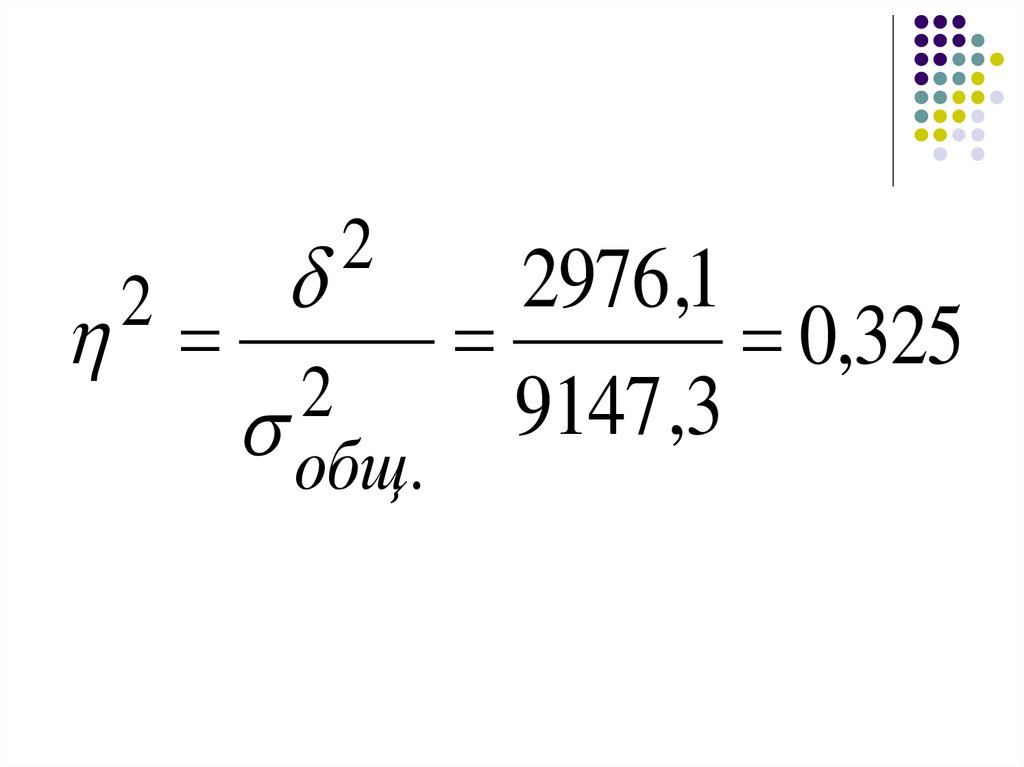


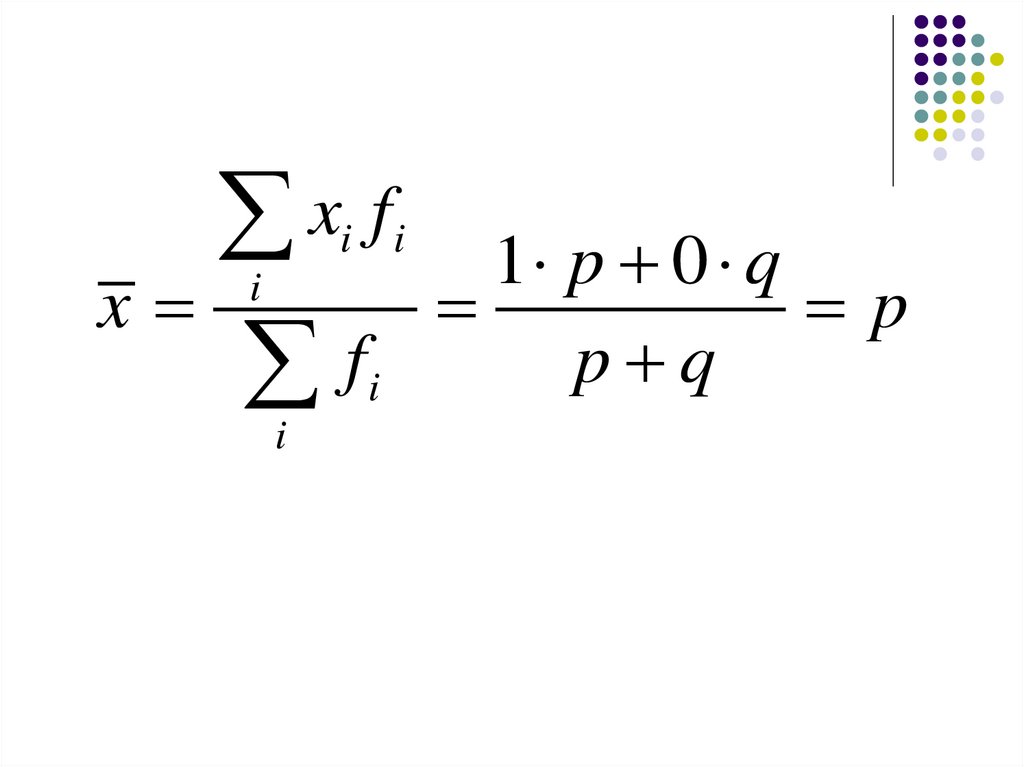


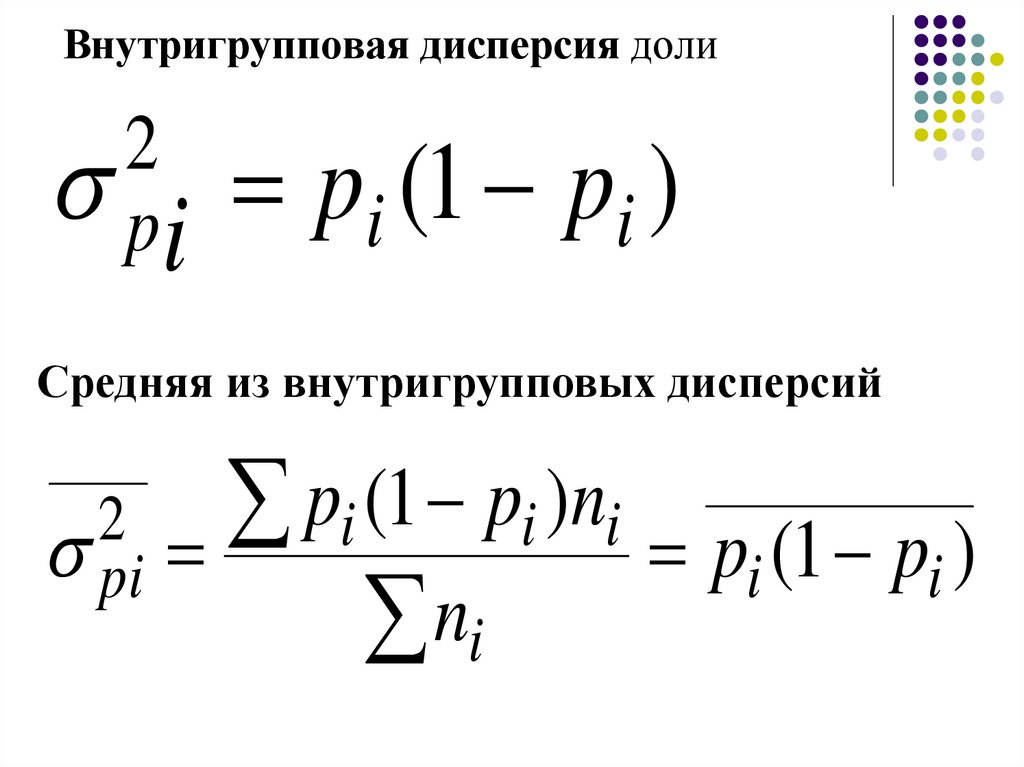








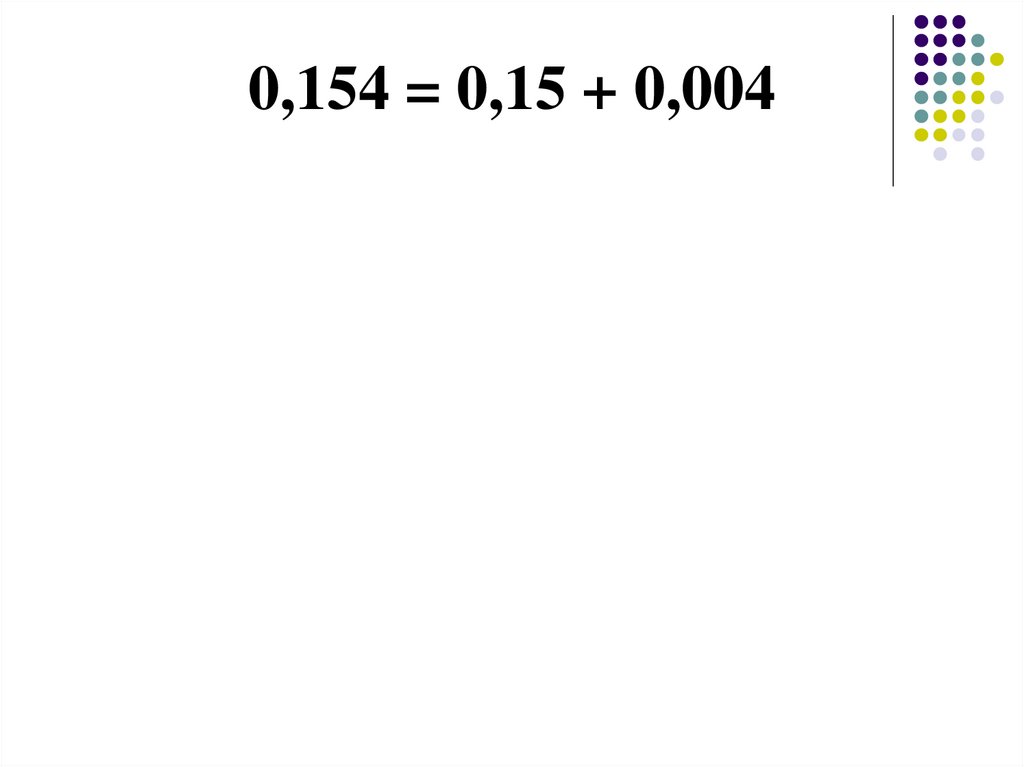
 Математика
Математика








