Представление информации в вычислительных машинах (тема 1)

1.

Информационнологические основы
построения
вычислительных машин
Тема 1 -Представление информации в
вычислительных машинах

2.

Информация
Понятие «информация» - фундаментальное понятие в науке и
базовое для информатики.
В простейшем (бытовом) понимании, с термином «информация»
обычно ассоциируются сведения, данные, знания и т.п.
Информация передается в виде «сообщений»,
определяющих форму и представление
передаваемой информации.
При этом предполагается, что имеются
«источник информации» и «получатель информации».
Примерами сообщений являются музыкальное произведение;
телепередача; команды регулировщика на перекрестке; текст,
распечатанный на принтере; данные, полученные в результате
работы составленной программы, и т.д.

3.

Представление числовой
информации. Системы счисления.
Как известно, для записи числовой информации
используют числа, состоящие из цифр.
Число — это некоторая абстрактная сущность
для описания количества
(определение из Википедии).
Цифры — это знаки, используемые для записи
чисел.
Цифры бывают разные, самыми
распространёнными являются арабские цифры,
представляемые известными нам знаками от нуля
(0) до девяти (9); менее распространены римские
цифры, мы их можем иногда встретить на
циферблате часов или в обозначении века (XIX
век).
{0,1,2,3,4,5,6,7,8,9 } ; {A,B,C,D,E,F}; {I, V, X, L, C, D, M }

4.

Системы счисления
Системы счисления определяют правила
записи чисел с помощью цифр.
Существует множество способов записи чисел с
помощью цифр.
Количество цифр используемых в системе
счисления называется «основанием системы
счисления».
Системы счисления бывают:
позиционными,
непозиционными
смешанными

5.

Виды систем счисления
Система счисления
Позиционная
Двоичная
Десятичная
Восьмеричная
Шестнадцатеричная
Непозиционная
Римская

6.

Цифры в системах счисления
Для записи чисел системы счисления с основанием до 36
включительно в качестве цифр используются арабские цифры (0,
1, 2, 3, 4, 5, 6, 7, 8, 9) и затем буквы латинского алфавита (A, B, C, D,
E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z). При этом, A = 10,
B = 11 и т. д., иногда X = 10.
При одновременной работе с несколькими системами счисления
для их различения основание системы обычно указывается в виде
нижнего индекса, который записывается в десятичной системе:
12310 — это число 123 в десятичной системе счисления;
11110112 — то же число, но в двоичной системе.

7.

Первые позиционные системы
счисления
Самой первой такой системой, когда счетным "прибором"
служили пальцы рук, была пятеричная.
Следующей возникла двенадцатеричная система счисления.
Возникла она в древнем Шумере. Возможно, что она возникала у
них из подсчёта фаланг на руке большим пальцем.
На ее широкое использование в прошлом указывает
сохранившиеся в ряде стран способы отсчета времени, денег и
соотношения между некоторыми единицами измерения. Год
состоит из 12 месяцев, а половина суток состоит из 12 часов.
Элементом двенадцатеричной системы в современности может
служить счёт дюжинами.
Английский фунт состоит из 12 шиллингов.

8.

Следующая позиционная система счисления была
придумана еще в Древнем Вавилоне, причем вавилонская
нумерация
была
шестидесятеричная,
т.е.
в
ней
использовалось шестьдесят цифр!
В более позднее время использовалась арабами, а также
древними
и
средневековыми
астрономами.
Шестидесятеричная система счисления, как считают
исследователи, являет собой синтез уже вышеупомянутых
пятеричной и двенадцатеричной систем.
В настоящее время наиболее распространены десятичная,
двоичная, восьмеричная и шестнадцатеричная системы
счисления.

9.

Позиционные системы счисления
Позиционная система счисления — система счисления, в которой
один и тот же числовой знак (цифра) в записи числа имеет
различные значения в зависимости от того места (разряда), где он
расположен.
Каждая позиционная система счисления определяется некоторым
числом b (т. н. основание системы счисления).
Система счисления с основанием b также называется
b-ричной (в частности, двоичной, троичной, десятичной и т. п.).

10.

Свойства позиционных систем
счисления
Основанием позиционной системы счисления называется количество знаков или
символов, используемых для изображения числа в данной системе счисления.
Основание системы счисления показывает во сколько раз изменяется количественное
значение цифры при перемещении её на соседнюю позицию
Основание системы счисления в ней самой всегда записывается как 10; например, в
двоичной системе счисления 10 означает число 2. За основание системы можно
принять любое натуральное число не менее 2
Базисом позиционной системы счисления называется последовательность чисел,
каждое из которых задает количественное значение или «вес» каждого разряда.
Например: Базисы некоторых позиционных систем счисления.
Десятичная система: 100, 101, .., 104,.. 10n,.. Двоичная система: 20, ... 23, 24,.., 2n,..
Восьмеричная система: 80, 81, 82, 83, 84,…, 8n,…
Пример. Десятичное число 4718,63, двоичное число 1001,1, восьмеричное число 7764,1,
шестнадцатеричное число 3АF.
Сравнение чисел. Сравним числа 321 и 312. Для этого слева направо сравниваем
цифры, стоящие в одинаковых разрядах: 3 = 3 — результат сравнения чисел не
определён; 2 > 1 — первое число больше независимо от оставшихся цифр.

11.

Позиционные системы счисления
В позиционной системе счисления значимость цифры
зависит от её расположения в числе.
Количество цифр в числе определяет его разрядность,
а вес данного разряда зависит от его позиции в числе.
Вес каждого следующего разряда в P раз больше предыдущего, где
P-основание позиционной системы.
На практике любое многоразрядное десятичное число имеет
краткую запись без указания веса разряда.
XB=A(n-1)A(n-2)…A1A0 , A-1A-2…A-S.
X10=123325,8=
= 1*105+2*104+3*103+3*102+2*101+5*100+8*10-1.

12.

Все позиционные системы счисления «одинаковы», а
именно, во всех них выполняются арифметические
операции по одним и тем же правилам:
справедливы одни и те же законы арифметики:
-коммутативный (переместительный):
m+n=n+m
m·n=n·m
-ассоциативный (сочетательный): (m + n) + k = m + (n + k) = m + n + k
(m · n) · k = m · (n · k) = m · n · k
-дистрибутивный (распределительный): (m + n) · k = m · k + n · k
справедливы правила сложения, вычитания и
умножения столбиком (Сложение чисел. Сложим 321 и 312. Для этого
справа налево складываем отдельные цифры);
правила выполнения арифметических операций
опираются на таблицы сложения и умножения.

13.

Позиционные системы
Десятичная система: первоначально – счет на пальцах
изобретена в Индии, заимствована арабами, завезена в Европу
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Основание (количество цифр): 10
сотни десятки единицы
2
1
3 7 8
300 70
разряды
0
= 3·102 + 7·101 + 8·100
8
Другие позиционные системы:
• двоичная, восьмеричная, шестнадцатеричная (информатика)
• двенадцатеричная (1 фут = 12 дюймов, 1 шиллинг = 12 пенсов)
• двадцатеричная (1 франк = 20 су)
• шестидесятеричная (1 минута = 60 секунд, 1 час = 60 минут)
14

14.

Десятичная система
счисления
Десятичная система счисления
— позиционная система счисления
по основанию 10.
Предполагается, что основание 10
связано с количеством пальцев на
руках у человека.
Наиболее распространённая
система счисления в мире.
Для записи чисел используются
символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
называемые арабскими цифрами.

15.

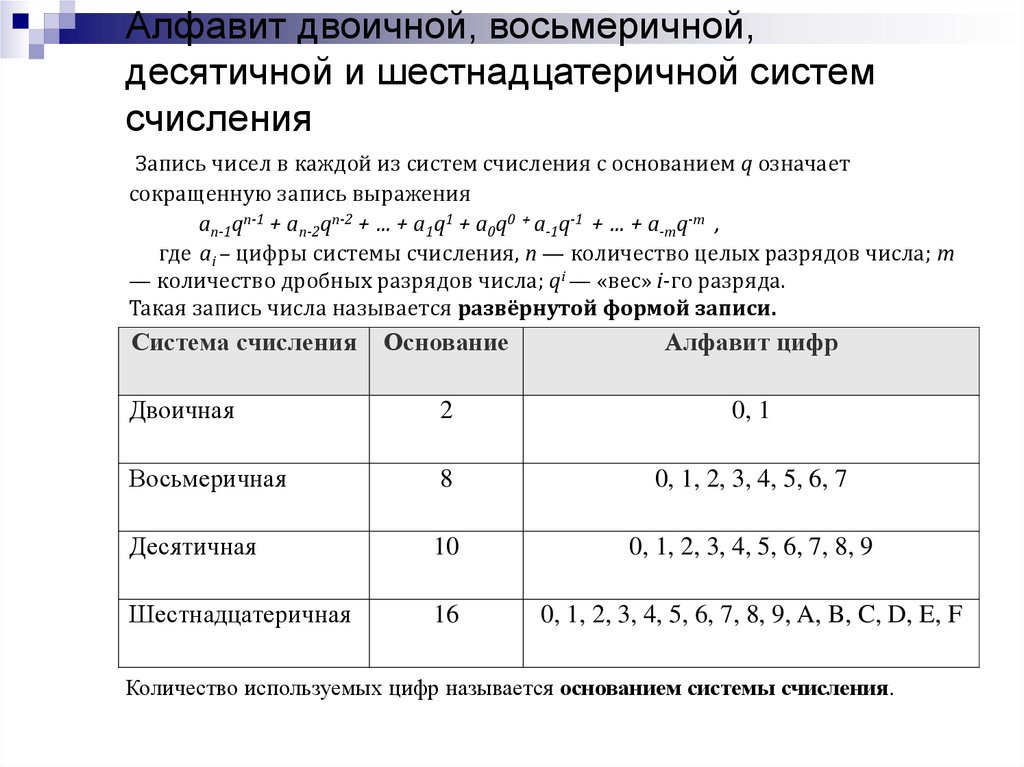
Алфавит двоичной, восьмеричной,
десятичной и шестнадцатеричной систем
счисления
Запись чисел в каждой из систем счисления с основанием q означает
сокращенную запись выражения
an-1qn-1 + an-2qn-2 + … + a1q1 + a0q0 + a-1q-1 + … + a-mq-m ,
где ai – цифры системы счисления, n — количество целых разрядов числа; m
— количество дробных разрядов числа; qi — «вес» i-го разряда.
Такая запись числа называется развёрнутой формой записи.
Система счисления
Основание
Алфавит цифр
Двоичная
2
0, 1
Восьмеричная
8
0, 1, 2, 3, 4, 5, 6, 7
Десятичная
10
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Шестнадцатеричная
16
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Количество используемых цифр называется основанием системы счисления.

16.

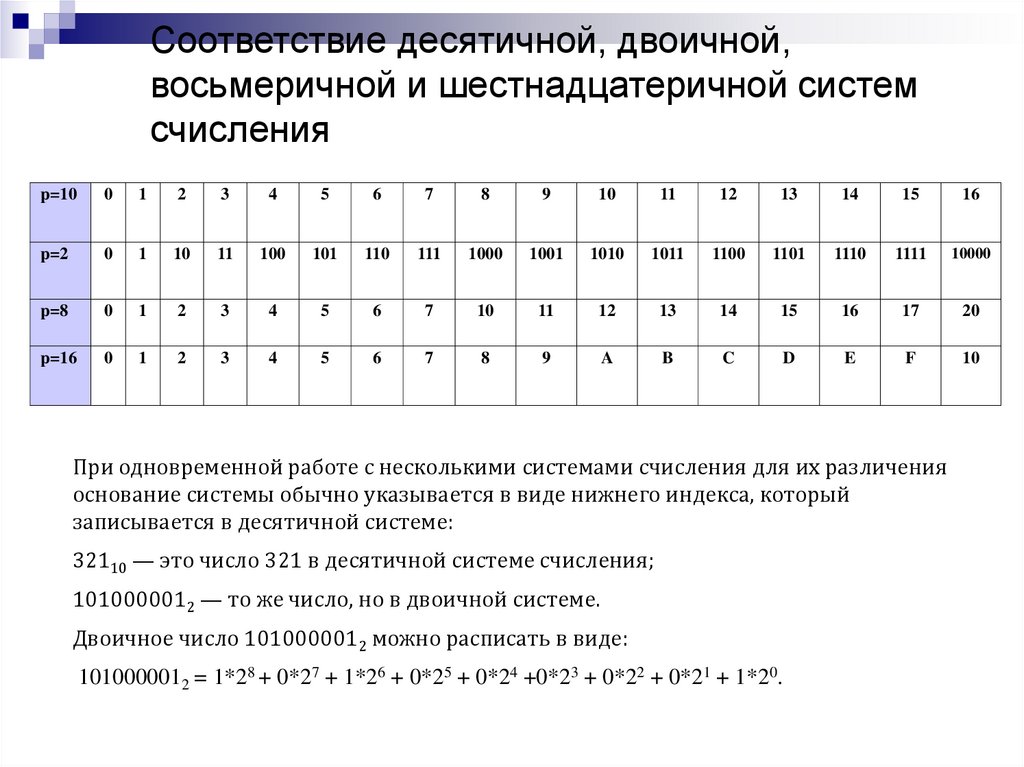
Соответствие десятичной, двоичной,
восьмеричной и шестнадцатеричной систем
счисления
p=10
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
p=2
0
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
1101
1110
1111
10000
p=8
0
1
2
3
4
5
6
7
10
11
12
13
14
15
16
17
20
p=16
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
10
При одновременной работе с несколькими системами счисления для их различения
основание системы обычно указывается в виде нижнего индекса, который
записывается в десятичной системе:
32110 — это число 321 в десятичной системе счисления;
1010000012 — то же число, но в двоичной системе.
Двоичное число 1010000012 можно расписать в виде:
1010000012 = 1*28 + 0*27 + 1*26 + 0*25 + 0*24 +0*23 + 0*22 + 0*21 + 1*20.

17.

Двоичная система счисления
В компьютерной технике очень часто используется двоичная система счисления. Такую
систему очень легко реализовать в железе (кремнии, транзисторах, микросхемах), так
как для нее требуется всего два устойчивых состояния (0 и 1).
Двоичная система счисления является позиционной системой. В ней используется две
цифры: 0 и 1.
Компьютеры используют двоичную систему так как к её достоинствам относится:
Использование элементной базы микроэлектроники с 2-мя устойчивыми
состояниями.
Использование аппарата булевой алгебры для выполнения логических
преобразований информации.
Использование простейшей арифметик - двоичная арифметика намного проще
десятичной
Представление информации с помощью только двух состояний надежно и
помехоустойчиво,

18.

Двоичная система счисления
Двоичная система счисления — позиционная система счисления с основанием 2.
Используются цифры 0 и 1.
Двоичная система используется в цифровых устройствах, поскольку является наиболее
простой и удовлетворяет требованиям:
Чем меньше значений существует в системе, тем проще изготовить отдельные
элементы.
Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем
быстрее он может работать.
Простота создания таблиц сложения и умножения — основных действий над
числами
Двоичная система, удобная для компьютера, для человека неудобна из-за её
громоздкости и непривычной записи. Для того, чтобы понимать слово компьютера,
разработаны восьмеричная и шестнадцатеричная системы счисления. Числа в этих
системах требуют в 3/4 раза меньше разрядов, чем в двоичной системе. Недостаток
двоичной системы является необходимость использования большого числа
символов при записи даже сравнительно небольших чисел, что существенно
затрудняет их восприятие человеком. Например, число 1567 записывается в
двоичном виде как 11000011111, а число 8763 — как 10001000111011 Поэтому для
интерпретации двоичной информации используется шестнадцатеричная система,
запись чисел в которой значительно компактнее.

19.

Развёрнутая форма
Согласно формуле (1.2) число в двоичной системе представляется в
виде
Aq =±(an–1 qn–1+ an–2 qn–2+…+ a0 q0+ a–1 q–1+…+ a–m q–m)
где каждое ai — одна из цифр 0 или 1
Примеры записи чисел в развёрнутой форме:
1012 = 1 ∙ 22 + 0 ∙ 21 + 1 ∙ 20 = 1 ∙ 4 + 1
101002 = 1 ∙ 24 + 0 ∙ 23 + 1 ∙ 22 + 0 ∙ 21 + 0 ∙ 20 = 1 ∙ 16 + 1 ∙ 4 = 20
2012=2 103 +0 102 +1 101 +2 100
0,125=1 10-1 +2 10-2 +5 10–3
14351,1=1 104 +4 103 +3 102 +5 101 +1 100 +1 10–1

20.

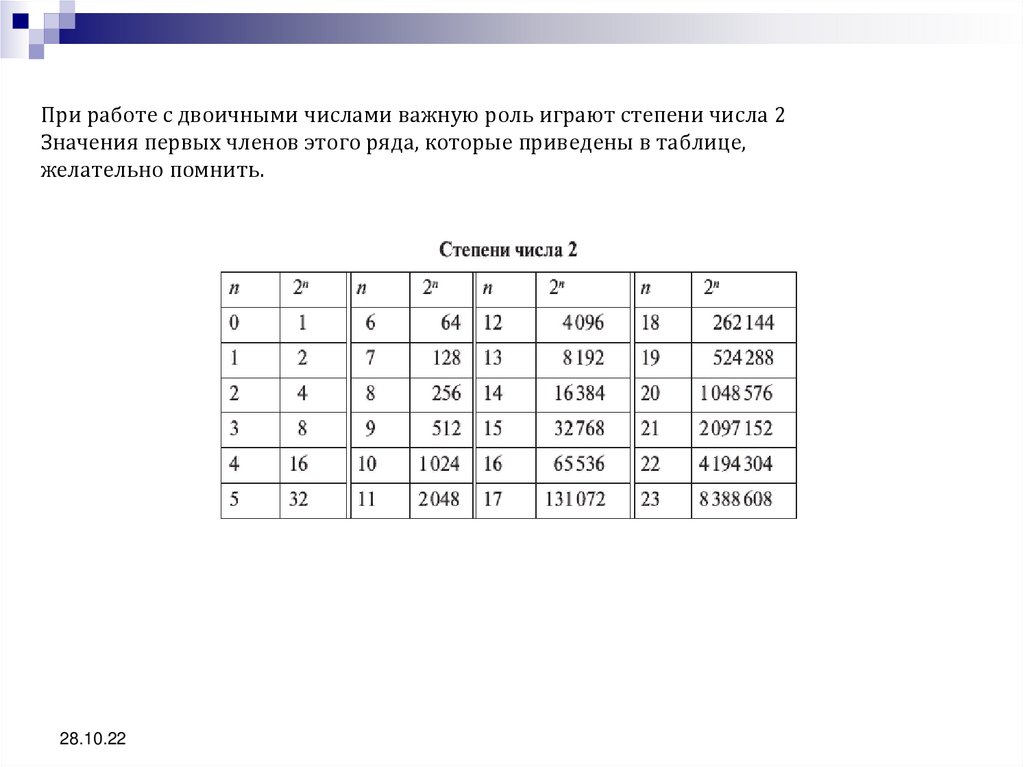
При работе с двоичными числами важную роль играют степени числа 2
Значения первых членов этого ряда, которые приведены в таблице,
желательно помнить.
28.10.22

21.

Все арифметические действия, которые применимы к двоичным числам,
выполняются аналогично как в десятичной системе. Удобнее всего
двоичные числа складывать, вычитать, умножать и делить столбиком.
Для того чтобы лучше освоить двоичную систему счисления, необходимо
освоить выполнение арифметических действий над двоичными числами.
Все позиционные системы счисления”одинаковы”, а именно, во всех них
арифметические операции выполняются по одним и тем же правилам:
справедливы одни и те же законы арифметики: коммутативный,
ассоциативный, дистрибутивный;
справедливы правила сложения, вычитания, умножения и деления
столбиком;
Правила выполнения арифметических операций опираются на таблицы
сложения и умножения.

22.

Двоичная арифметика
Арифметика двоичной системы счисления
основывается на использовании следующих таблиц
сложения :
02 + 02 = 0 2
+
0
1
02 + 12 = 1 2
0
0
1
1
1
10
12 + 02 = 1 2
или
12 + 12 = 102 (результат сложения двух единиц: ноль
и единица переноса в старший разряд)

23.

Сложение двоичных чисел выполняются в
столбик.
Примеры:
10110
1001
+ 101 + 1010
11011 10011
1111
101,011
+
1 + 1,11
10000
111 ,001
Например, сумма двоичных чисел 1000111 + 110011 = 1111010
На примере видно, как происходит перенос в старший разряд. При сложении единиц самого
младшего разряда получается 10. Ноль остается на своем месте, а единица переносится в
старший разряд слева, где уже складываются две единицы. Получается 11. И снова, младшую
единицу оставляют, а старшую переносят влево.

24.

Двоичная арифметика
Арифметика двоичной системы счисления
основывается на использовании следующих таблиц
сложения и умножения:
0 2 × 02 = 0 2
0
1
0 2 × 12 = 02
0
0
0
1
0
1
1 2 × 02 = 0 2
1 2 × 12 = 12
или

25.

Умножение двоичных чисел производится в столбик
аналогично умножению десятичных чисел.
Примеры:
1011
*101
+ 1011
1011
110111
1101
*11
1101
+1101
100111

26.

Вычитание
Правила вычитания:
0-0=0
1-0=1
1-1=0
10-1=1 (из нуля вычесть единицу нельзя,
поэтому для вычитания необходимо
занять единицу у старшего разряда)

27.

При выполнении операции вычитания всегда из
большего по абсолютной величине вычитается
меньшее и у результата ставится соответствующий
знак.
Примеры:
1011
-111
100
1001
-110
11
11-1011= -(1011-11)
1011
- 11
1000

28.

Деление
Деление в двоичной системе счисления выполняется, как и в десятичной
системе.
Пример:
10101 111
- 111 11
1 11
- 1 11
0

29.

Восьмеричная и шестнадцатеричная системы
счислений
Компьютерам очень удобно оперировать двоичными
числами, но люди не привыкли работать с большим
количеством цифр.
Поэтому были придуманы восьмеричная и
шестнадцатеричная системы счислений.
Они удобны, как и десятичные числа тем, что для
представления числа требуется меньшее количество
разрядов, а по сравнению с десятичными числами,
перевод в двоичное представление очень простой.
Это как будто мы двоичное число разбили на группы
по три или четыре разряда и каждой двоичной
комбинации придумали значок.

30.

Восьмеричная система счисления
Восьмеричной системой счисления называется позиционная система
счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
an–1an–2…a1a0 = an–1 8n–1+an–2 8n–2+…+a0 80
Для перевода целого восьмеричного числа в десятичную систему
счисления следует перейти к его развёрнутой записи и вычислить значение
получившегося выражения.
Для перевода восьмеричного числа в десятичное необходимо его
записать в виде многочлена, состоящего из произведений цифр числа и
соответствующей степени числа 8, и вычислить по правилам десятичной
арифметики.
Пример: 10638 =1 83 +0 82+6 81+3 80=56310.
Для перевода целого десятичного числа в восьмеричную систему
счисления следует последовательно выполнять деление данного числа и
получаемых целых частных на 8 до тех пор, пока не получим частное, равное
нулю.

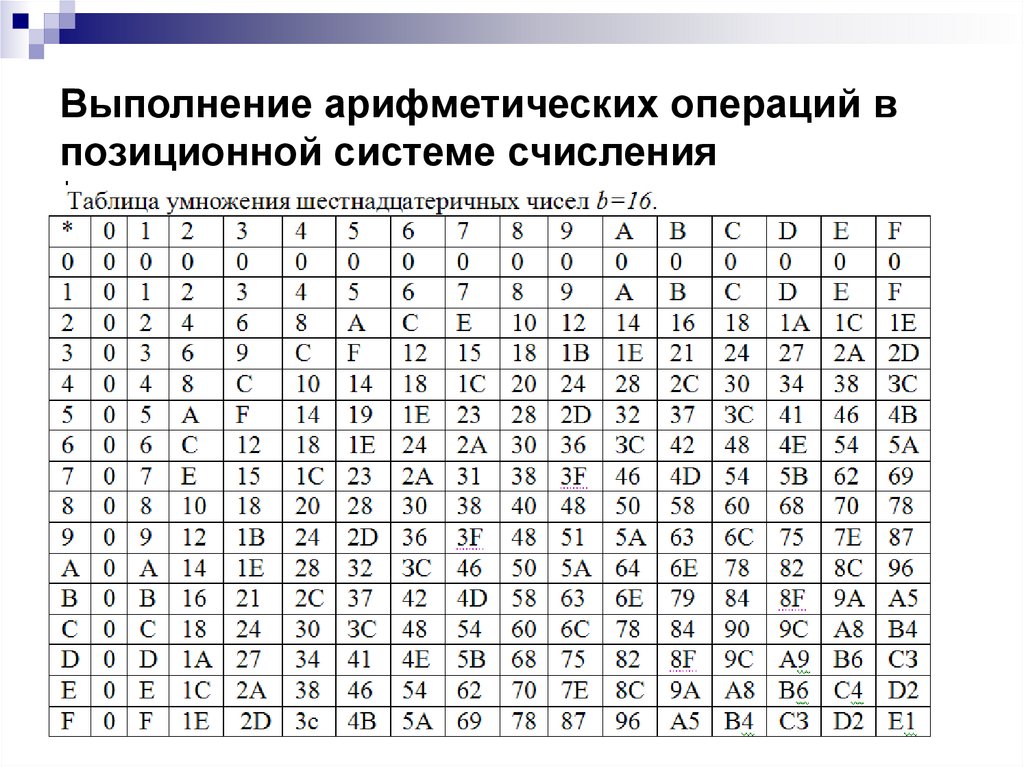
31.

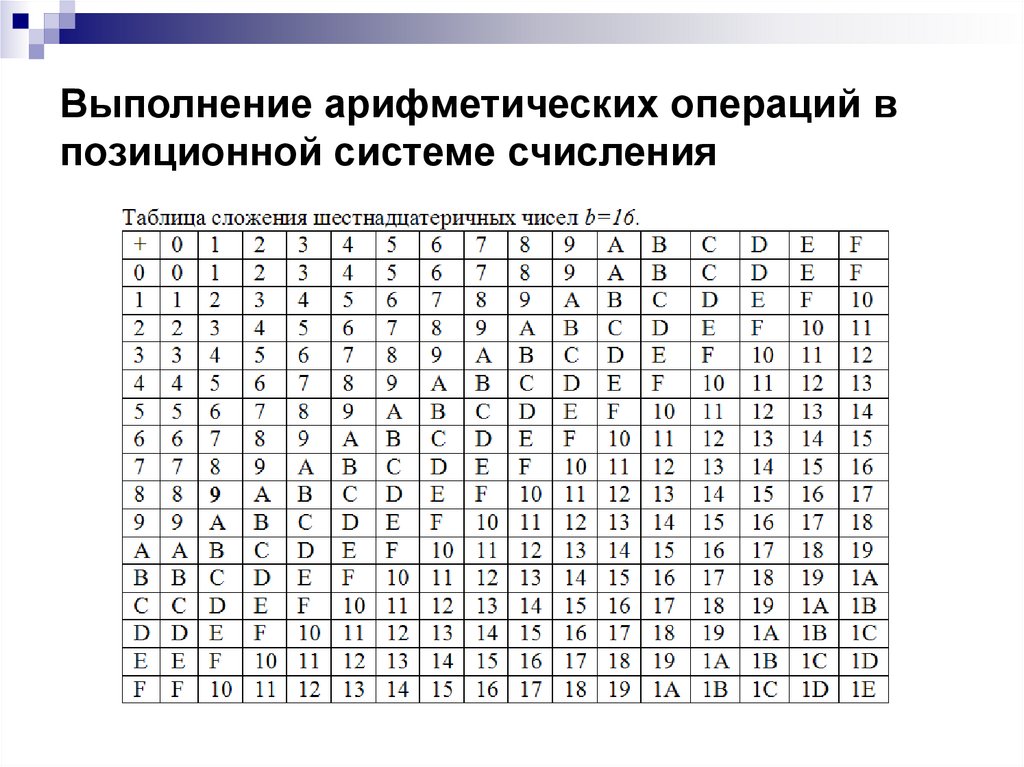
Выполнение арифметических операций в
позиционной системе счисления

32.

Шестнадцатеричная система счисления
Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
3АF16 =3 162+10 161+15 160 =768+160+15=94310.
Переведём десятичное число 154 в шестнадцатеричную
систему счисления
154 16
-144
9
16
10
(А)
9
0
15410 = 9А16

33.

Выполнение арифметических операций в
позиционной системе счисления

34.

Выполнение арифметических операций в
позиционной системе счисления

35.

Перевод из десятичной в b-ичную (b>1) 10 b
1) если переводится целая часть числа, то она делится на b, после чего
запоминается остаток от деления.
Полученное частное вновь делится на b, остаток запоминается.
Процедура продолжается до тех пор, пока частное не станет равным
нулю.
Остатки отделения на b выписываются в порядке, обратном их
получению;
2) если переводится дробная часть числа, то она умножается на b,
после чего целая часть запоминается и отбрасывается.
Вновь полученная дробная часть умножается на b и т.д.
Процедура продолжается до тех пор, пока дробная часть не станет
равной нулю.
Целые части выписываются после двоичной запятой в порядке их
получения.
Результатом может быть либо конечная, либо периодическая двоичная
дробь. Поэтому, когда дробь является периодической, приходится
обрывать умножение на каком-либо шаге и довольствоваться
приближенной записью исходного числа в системе с основанием b.

36.

Перевод из двоичной в восьмеричную и
шестнадцатеричную системы 2 8, 2 16
Если необходимо перевести число из двоичной системы
счисления в систему счисления, основанием которой
является степень двойки, достаточно объединить
цифры двоичного числа в группы по столько цифр,
каков показатель степени. 8 – три, 16 – четыре.
В целой части числа группировка производится справа
налево, в дробной части — слева направо.
0001 1111, 0010 1000 или 001 111, 001 010
Если в последней группе недостает цифр, дописываются
нули: в целой части — слева, в дробной — справа.
Затем каждая группа заменяется соответствующей
цифрой новой системы.

37.

Таблицы перевода 2 8
Способ 1:
Для перевода в восьмеричную систему нужно разбить двоичное число на группы по 3
цифры справа налево. В последней (самой левой) группе вместо недостающих цифр
поставить слева нули. Для каждой полученной группы произвести умножение
каждого разряда на 2n, где n - номер разряда.
11012 = (001) (101) = (0*22 + 0*21 + 1*20) (1*22 + 0*21 + 1*20) = (0+0+1) (4+0+1) = (1) (5) =
= 158
Способ 2:
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в
скобках просто заменим полученные группы (триады) на соответствующие цифры
восьмеричной системы, используя таблицу триад:
101110102 = (010) (111) (010) = 2728
1011010,011012 = 001 011 010,011 0102 = 132,328
28.10.22

38.

Таблицы перевода 2 16
Способ 1:
Разбиваем число на группы по 4 цифры справа налево. Последнюю (левую) группу
дополним при необходимости ведущими нулями. Внутри каждой полученной группы
произведем умножение каждой цифры на 2n, где n - номер разряда, и сложим результаты.
110102 = (0001) (1010) = (0*23 + 0*22 + 0*21 + 1*20) (1*23 + 0*22 + 1*21 + 0*20) = (0+0+0+1)
(8+0+2+0) = (1) (10) = 1A16
Способ 2:
Также как и в первом способе разбиваем число на группы по 4 цифры, на квартеты.
Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной
системы, используя таблицу тетрад:
1011010110,0110012 = 0010 11 01 0110,011 0102 = 132,328
1011111002 = (0001) (0111) (1100) = 17C16

39.

Перевести число 11001010011010101112
в шестнадцатеричную систему счисления
0110 0101 0011 0101 0111
6
5
3
5
7
Получаем
6535716

40.

Перевод произвольной позиционной
системы счисления в десятичную b 10
При переводе чисел из системы счисления с основанием b в
десятичную систему счисления необходимо пронумеровать
разряды целой части справа налево, начиная с нулевого, и
дробной части, начиная с разряда сразу после запятой,
слева направо (начальный номер — 1).
Затем вычислить сумму произведений соответствующих
значений разрядов на основание системы счисления в
степени, равной номеру разряда. Это и есть представление
исходного числа в десятичной системе счисления.
Например: 1100,0112 =12,375
11002= 1 · 23 + 1 · 22 + 0 · 21 + 0 · 1 = 1 · 8 + 1 · 4 +
+ 0 · 2 + 0 · 1 = 8 + 4 + 0 = 1210
0,0112 =0*2-1+1*2-2+1*2-3=0+0,25+0,125=0,375
Переведем десятичное число 2010 в двоичную систем счисления (основание
системы счисления p=2). В итоге получили 2010 = 101002.

41.

Перевод чисел из любой позиционной
системы счисления в десятичную
Чтобы перевести целое число из позиционной системы счисления с
основанием b в десятичную, нужно справа налево, начиная с 0,
расставить разряды, потом каждую цифру умножить на основание
системы счисления из которой переводим в степени этого разряда.
Например, переведем число 110012 в десятичную систему счисления.
Для этого представим это число в виде степеней двойки и
произведем вычисления в десятичной системе счисления.
4 3 2 1 0
110012 = 1*24 + 1*23 + 0*22 + 0*21 + 1*20 = 1*16 +1*8 + 0*4 +
0*2 + 1*1 = 16 + 8 + 0 + 0 + 1 = 2510
Рассмотрим еще один пример. Переведем число 12,348 в десятичную
систему счисления.
1 0
-1 -2
12,348 = 1*81 + 2*80 + 3*8-1 + 4*8-2 = 1*8 + 2*1 + 3*1/8
+4*1/64 = 10 + 0,375 + 0,0625 = 10,437510

42.

Правило перевода целых десятичных чисел
в систему счисления с основанием q
1) последовательно выполнять деление данного числа и
получаемых целых частных на основание новой системы
счисления до тех пор, пока не получим частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в
новой системе счисления, привести в соответствие с
алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая
его, начиная с последнего полученного остатка.

43.

Позиционные системы
Пример - в какой системе счисления число 58
записывается как «46x»? Определите основание системы
счисления X.
58 = 46x
• в записи есть цифра 6, поэтому x > 6
• переводим правую часть в десятичную систему
1 0
58 = 46x = 4·x1 + 6·x0= 4·x + 6
• решаем уравнение
58 = 4·x + 6
44
x = 13

44.

Позиционные системы
Пример- найдите основание системы счисления, в
которой выполняется равенство
16x + 33x = 52x
• в записи есть цифра 6, поэтому x > 6
• переводим в десятичную систему
1 0
16x = x + 6
1 0
52x = 5·x + 2
33x = 3·x + 3
• решаем уравнение
4·x + 9 = 5·x + 2
45
x= 7

45.

Позиционные системы
Пример- перечислите через запятую все системы
счисления, в которых выполняется неравенство
21x + 32x > 102x
• в записи есть цифра 3, поэтому x > 3
• переводим в десятичную систему
1 0
2 1 0
21x = 2·x + 1
102x = x2 + 2
32x = 3·x + 2
• решаем неравенство (перебор x = 4, 5, 6, …)
5·x + 3 > x2 + 2
46
x = 4,5

46.

ПЕРЕВОД ЦЕЛОГО ДЕСЯТИЧНОГО ЧИСЛА
МЕТОДОМ ПОЭТАПНОГО ДЕЛЕНИЯ
Перевести десятичное число 26 в двоичную,
троичную, шестнадцатеричную системы
2610→Х2
26
13
6
3
1
0
1
0
1
1
2610=110102
2610→Х3
26 2
8 2
2 2
2610=2223
2610→Х16
26 10
1 1
2610=1А16

47.

Перевести десятичную дробь
0,375
0 375
* 2
0 750
2
1 500
2
1 000
0 375
*
3
1 125
3
0 375
3
1 125
0 375
• 16
2 250
3 75
6 000
0,37510=0,0112 0,37510=0,1013 0,37510=0,616

48.

Перевод целых чисел
Двоичная система:
Алфавит: 0, 1
Основание (количество цифр): 2
10 2
19
18
1
2
9
8
1
2
4
4
0
50
2
2
2
0
2 10
43210
19 = 100112
2
1
0
система
счисления
2
0
1
разряды
100112 = 1·24 + 0·23 + 0·22 + 1·21 + 1·20
= 16 + 2 + 1 = 19

49.

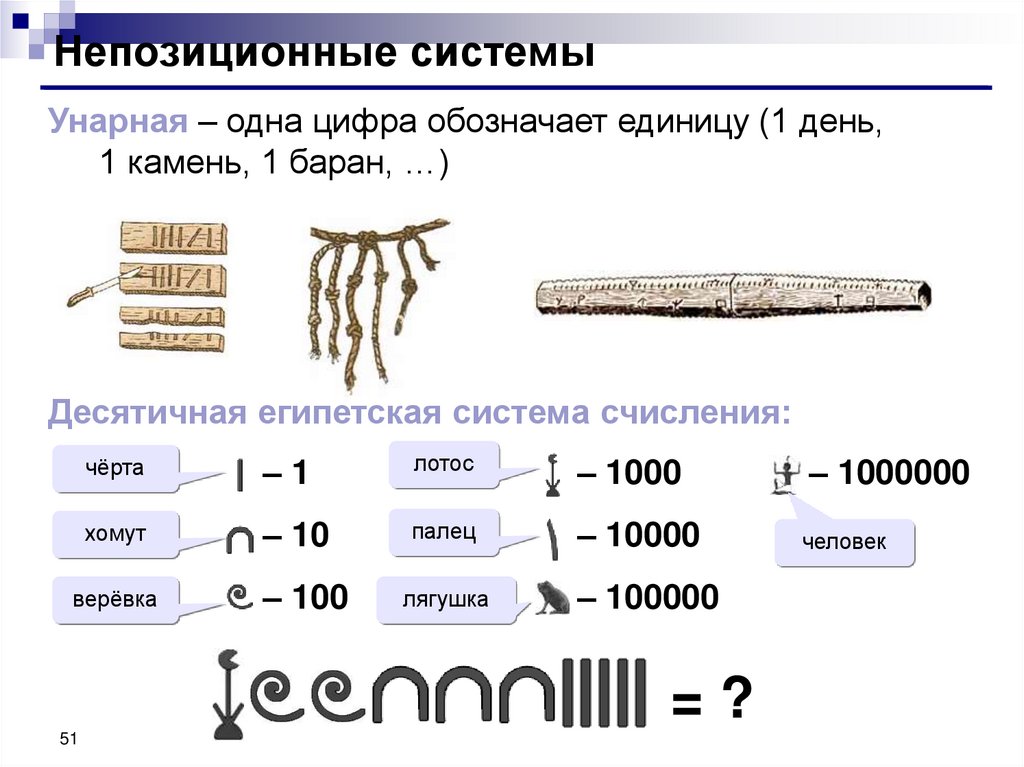
Непозиционные системы
Унарная – одна цифра обозначает единицу (1 день,
1 камень, 1 баран, …)
Десятичная египетская система счисления:
чёрта
–1
лотос
– 1000
– 1000000
хомут
– 10
палец
– 10000
человек
верёвка
– 100
лягушка
– 100000
=?
51

50.

Непозиционная система счисления
Система счисления называется непозиционной, если количественный
эквивалент (количественное значение) цифры в числе не зависит от её
положения в записи числа. Непозиционные системы счисления возникли
раньше позиционных. Они характеризуются тем, что в них символы,
обозначающие то или иное число, не меняют своего значения в зависимости
от своего местоположения в записи этого числа.
Классическим примером такой системы является римская система
счисления, в которой в качестве цифр используются латинские буквы:
1
I
100
C
5
V
500
D
10
X
1000
M
50
L

51.

Непозиционные системы
счисления
Натуральные числа записываются при помощи повторения
этих цифр. Например, II = 1 + 1 = 2, здесь символ I обозначает 1
независимо от места в числе.
Для правильной записи больших чисел римскими цифрами
необходимо сначала записать число тысяч, затем сотен, затем
десятков и, наконец, единиц.
Пример: число 1789. Одна тысяча M, семь сотен DCC, восемьдесят LXXX,
девять IX. Запишем их вместе: MDCCLXXXIX.
MDCCLXXXIX=1000+(500+100+100)+(50+10+10+10)+(10-1)=1789
Для изображения чисел в непозиционной системе счисления нельзя
ограничится конечным набором цифр. Кроме того, выполнение
арифметических действий в них крайне неудобно.

52.

Здесь алгоритмические числа получаются путём сложения и вычитания узловых
чисел с учётом следующего правила:
каждый меньший знак, поставленный справа от большего, прибавляется к его
значению, а каждый меньший знак, поставленный слева от большего, вычитается
из него.
Некоторые примеры чисел в римской системе счисления и их десятичные
эквиваленты приведены в табл.
28.10.22

53.

Римская система счисления
Правила:
(обычно) не ставят больше трех одинаковых цифр
подряд
если младшая цифра (только одна!) стоит слева от
старшей, она вычитается из суммы (частично
непозиционная!)
Примеры:
MDCXLIV = 1000 + 500 + 100 – 10 + 50 – 1 + 5 = 1644
2389 = 2000 + 300 +
MM
CCC
80
LXXX
2389 = M M C C C L X X X I X
55
+
9
IX

54.

Непозиционные системы счисления
В непозиционной системе счисления цифры не
меняют своего количественного значения при
изменении их расположения в числе.
Остальные значения чисел получаются из базовых
путём сложения (например, 700=DCC) или вычитания
(например, 800=CCM). В позиционной системе
счисления значение каждой цифры зависит от её места
(позиции) в числе.

55.

Римская система счисления
Недостатки:
для записи больших чисел (>3999) надо вводить
новые знаки-цифры (V, X, L, C, D, M)
как записать дробные числа?
как выполнять арифметические действия:
CCCLIX + CLXXIV =?
Где используется:
номера глав в книгах:
обозначение веков: «Пираты XX века»
циферблат часов
номера месяцев
57

56.

Славянская система счисления
алфавитная система счисления (непозиционная)
Часы
Суздальского
Кремля
58

57.

Смешанные системы счисления
Система счисления времени
Наиболее
известным примером смешанной
системы счисления являются представление
времени в виде количества суток, часов, минут и
секунд.
При этом величина d дней h часов m минут s секунд
соответствует значению:
d*24*60*60+h*60*60+m*60+s

58.

Смешанная система счисления
Смешанная система счисления является обобщением b-ричной
системы счисления и также зачастую относится к позиционным
системам счисления. Основанием смешанной системы счисления
является возрастающая последовательность чисел bk k 0
и каждое число x представляется как линейная комбинация :
n
X ak bk
k 0
где на коэффициенты ak (называемые как и прежде цифрами)
накладываются некоторые ограничения.
Записью числа x в смешанной системе счисления называется
перечисление его цифр в порядке уменьшения индекса k,
начиная с первого ненулевого.
Если bk = bk для некоторого b, то смешанная система счисления
совпадает с b-ричной системой счисления.

59.

Смешанные системы счисления
Денежные знаки - это пример смешанной системы счисления.
Сейчас в России используются монеты и купюры следующих
номиналов: 1 коп., 5 коп., 10 коп., 50 коп., 1 руб., 2 руб., 5 руб., 10 руб.,
50 руб., 100 руб., 500 руб., 1000 руб. и 5000 руб.
Чтобы получить некоторую сумму в рублях, нам нужно
использовать некоторое количество денежных знаков различного
достоинства.
Предположим, что мы покупаем пылесос, который стоит 6379 руб.
Чтобы расплатиться, нам потребуется шесть купюр по тысяче
рублей, три купюры по сто рублей, одна пятидесятирублёвая
купюра, две десятки, одна пятирублёвая монета и две монеты по
два рубля.
Если мы запишем количество купюр или монет начиная с 1000 руб.
и заканчивая одной копейкой, заменяя нулями пропущенные
номиналы, то мы получим число, представленное в смешанной
системе счисления; в нашем случае — 603121200000.

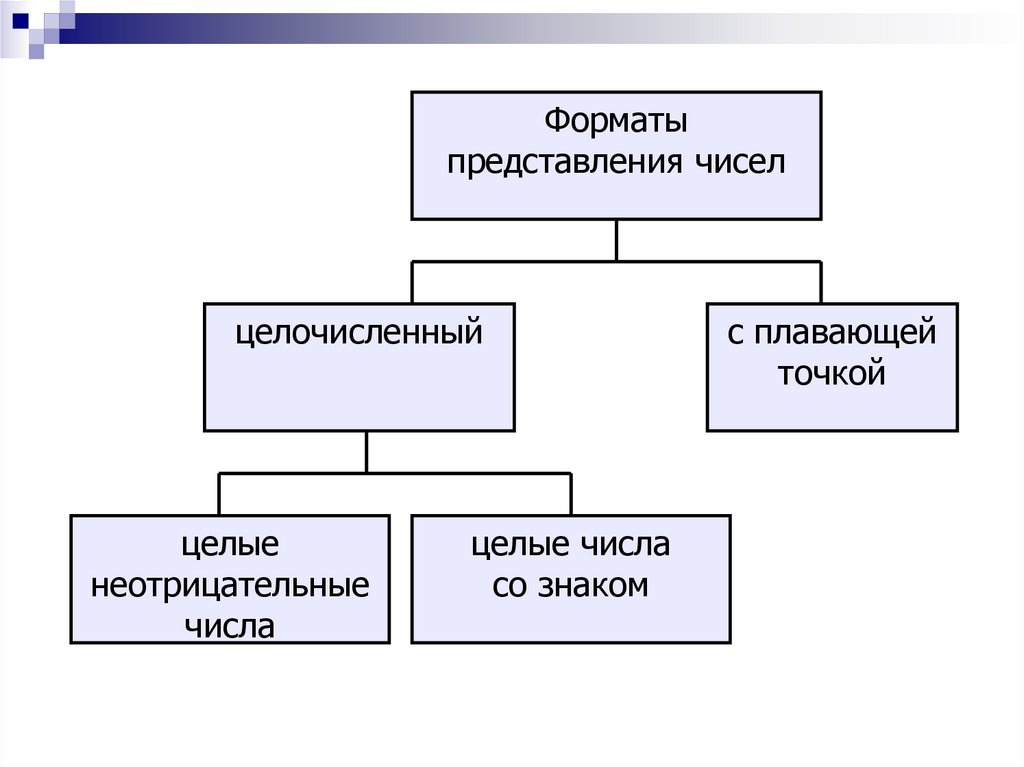
60.

Форматы
представления чисел
целочисленный
целые
неотрицательные
числа
целые числа
со знаком
с плавающей
точкой

61.

Плотность записи информации
При условии равновероятности появления каждой из
цифр плотность записи (т.е. количество информации на
одну позицию) чисел в системе счисления с основанием b
равна ln(b)/b.
Из систем счисления с целочисленными основаниями
наибольшей плотностью записи информации обладает
троичная система счисления.
Двоичная и четверичная системы счисления делят второе
место. Остальные целочисленные системы счисления
имеют меньшую плотность записи информации.

62.

Примеры позиционных систем счисления
С целочисленными основаниями:
1 — единичная (унарная) система счисления, c некоторыми
оговорками, относится к позиционным системам счисления.
2 — двоичная (в дискретной математике, информатике,
программировании)
3 — троичная система счисления
8 — восьмеричная (в программировании)
10 — десятичная система счисления
12 — двенадцатеричная (широко использовалась в древности, в
некоторых частных областях используется и сейчас)
16 — шестнадцатеричная (наиболее распространена в
программировании, а также в шрифтах)
40 — сорокаичная система счисления (применялась в древности
("сорок сороков = 1600"))
60 — шестидесятеричная (измерение углов и, в частности,
долготы и широты)

63.

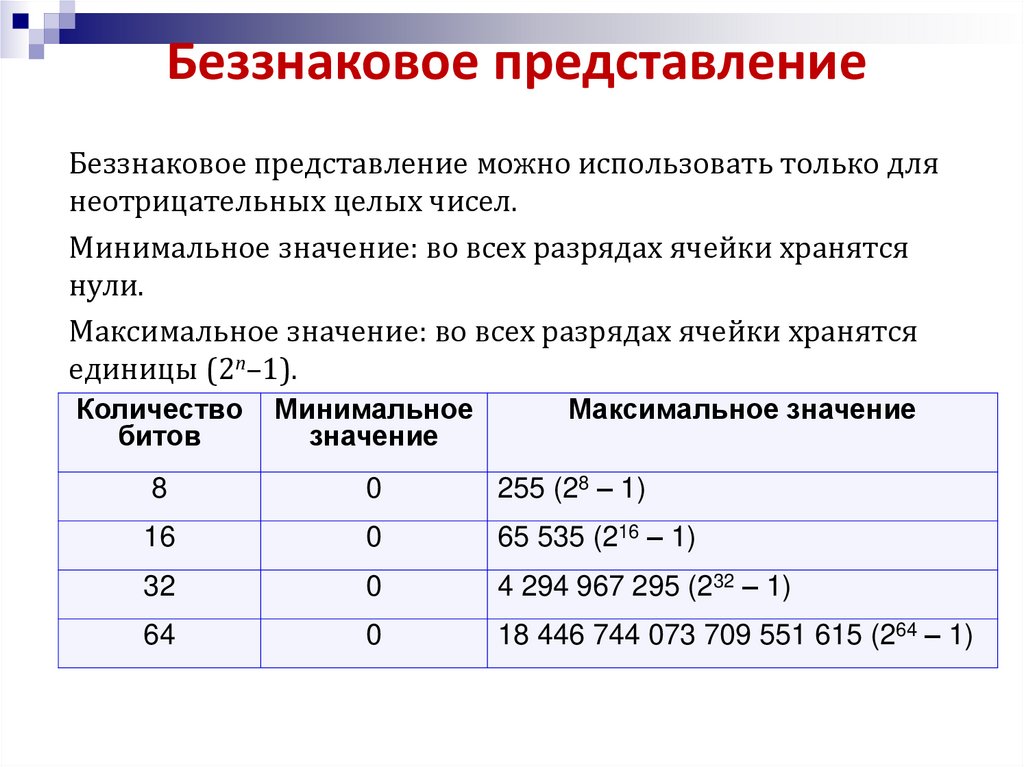
Беззнаковое представление
Беззнаковое представление можно использовать только для
неотрицательных целых чисел.
Минимальное значение: во всех разрядах ячейки хранятся
нули.
Максимальное значение: во всех разрядах ячейки хранятся
единицы (2n–1).
Количество
битов
Минимальное
значение
Максимальное значение
8
0
255 (28 – 1)
16
0
65 535 (216 – 1)
32
0
4 294 967 295 (232 – 1)
64
0
18 446 744 073 709 551 615 (264 – 1)

64.

Формат с плавающей запятой
Число в формате с плавающей запятой может занимать в
памяти компьютера 32 или 64 разряда.
При этом выделяются разряды для хранения
знака порядка, порядка, знака мантиссы и мантиссы.
0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Знак и порядок
Знак и мантисса
Диапазон представления вещественных чисел определяется
количеством разрядов, отведённых для хранения порядка
числа, а точность - количеством разрядов, отведённых для
хранения мантиссы.

65.

Прочие позиционные СС
Система счисления с основанием е=2,718281828...
Обладает наибольшей плотностью записи
информации. Относится к нецелочисленным
позиционным системам счисления.
Троичная система счисления
Из целочисленных систем счисления обладает
наибольшей плотностью записи информации. Первая
троичная ЭВМ "Сетунь" была построена Брусенцовым
в МГУ.
Четверичная система счисления
Обладает такой же плотностью записи, как и
двоичная система счисления.

66.

Прочие позиционные СС
Двенадцатеричная система счисления
С основанием 12 (дюжина). По плотности записи
информации уступает многим другим системам
счисления, но удобна для человека, так как 12 делится
на 12, на 6, на 4, на 3, на 2 и на 1 человека. Поэтому
сервизы делают на 12 персон, а яйца продают по 12
штук (дюжинами).

67.

Прочие позиционные СС
Шестидесятеричная система счисления
То как мы представляем время на часах это пример
шестидесятеричной позиционной системы счисления.
В представлении времени используется три позиции
для часов, минут и секунд; так как для каждой
позиций приходиться использовать 60 цифр, а у нас
только десять цифр, то для каждой
шестидесятеричной позиции используется две
десятичные цифры (00, 01, 02, ..., 59), а позиции
разделяются двоеточием.
h:m:s
Чтобы получить время в секундах мы должны
посчитать вот по такой формуле:
h602 + m601 + s600 = h3600 + m60 + s

68.

Представления информации в ЭВМ
Кодирование информации — понятие, отражающее
фундаментальную необходимость представления информации в
какой-либо форме. При этом слово «кодирование» понимается в
широком смысле как представление информации в виде сообщения
на каком-либо языке.
Для представления информации в памяти ЭВМ (как числовой, так и
нечисловой) используется двоичный способ кодирования.
Элементарная ячейка памяти ЭВМ имеет длину 8 бит (байт). Каждый
байт имеет свой номер (его называют адресом).
Наибольшую последовательность бит, которую ЭВМ может
обрабатывать как единое целое, называют машинным словом.
Длина машинного слова зависит от разрядности процессора и может
быть равной 16, 32, 64 битам и т.д.

69.

Двоичное кодирование в
компьютере
Вся информация, которую обрабатывает компьютер должна быть
представлена двоичным кодом с помощью двух цифр: 0 и 1.
Эти два символа принято называть двоичными цифрами или
битами.
С помощью двух цифр 0 и 1 можно закодировать любое
сообщение. Это явилось причиной того, что в компьютере
обязательно должно быть организованно два важных
процесса: кодирование и декодирование.
Кодирование – преобразование входной информации в форму,
воспринимаемую компьютером, т.е. двоичный код.
Декодирование – преобразование данных из двоичного кода в
форму, понятную человеку.

70.

Кодирование текста
Текстовая информация осмысленно воспринимается лишь в том
случае, если человек умеет читать и знает язык, на котором
написан текст.
Информация имеющая вид текста, часто представляется в виде
кода, в котором каждому отдельному символу в тексте
приписывается уникальная последовательность битов.
На заре развития вычислительной техники было разработано
много систем кодов, которые разрабатывались для различной
техники, что привело к проблемам при передаче информации.
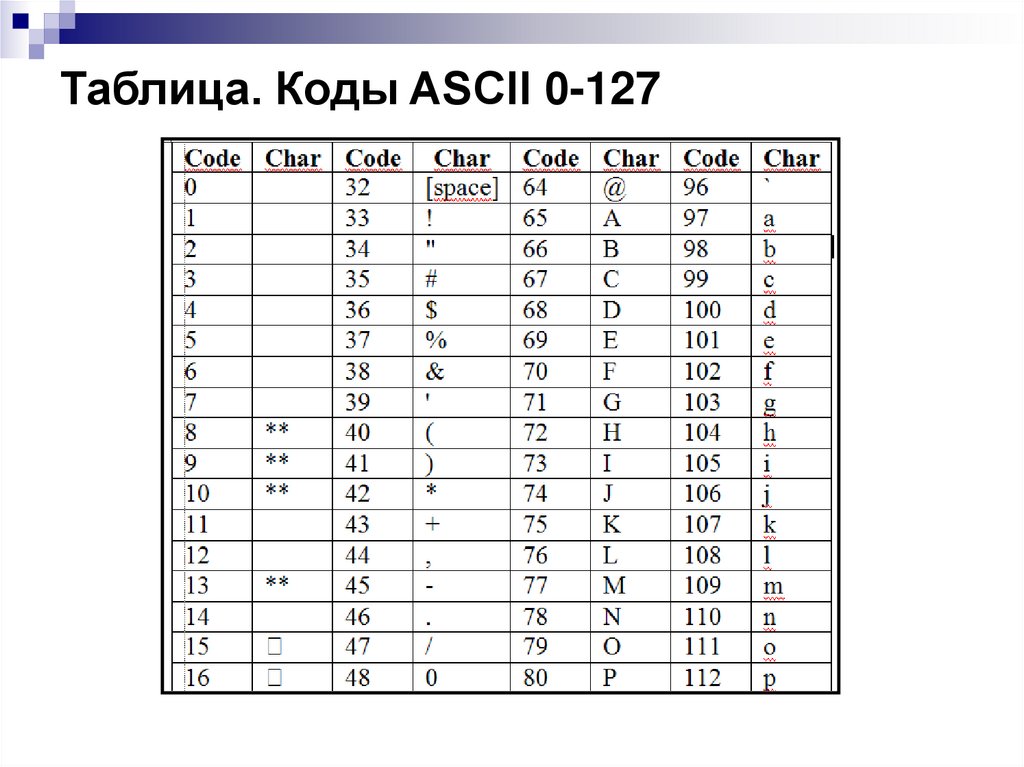
Для преодоления этой ситуации Американским национальным
институтом стандартов(ANSI) был принят американский
стандартный код для обмена информацией ASCII, в котором
используются наборы из 7 битов для представления строчных и
прописных символов английского алфавита, знаков пунктуации,
цифр и др . символов.
Сегодня для хранения кодов используется 8 бит, при этом
дополняя старший бит 0.
01001000
01100101
01101100
01101100
01101111
00101110
H
e
l
l
o
.

71.

Кодирование текста
Текстовая информация осмысленно воспринимается лишь в том
случае, если человек умеет читать и знает язык, на котором написан
текст.
Для умелого чтения необходимо знать буквенный и числовой
алфавиты.
В русском языке используется кириллица (32 буквы) и арабские
цифры от 0 до 9.
В английском языке используются буквы латинского алфавита
(26 букв).
Для кодирования символов достаточно одного байта. При этом можно
представить 256 символов (с десятичными кодами от 0 до 255).
Набор символов персональных ЭВМ IBM PC чаше всего является
расширением кода ASCII (American Standart Code for Information
Interchange — стандартный американский код для обмена
информацией).

72.

Таблица. Коды ASCII 0-127

73.

Двоично-десятичное кодирование
В некоторых случаях при представлении в памяти ЭВМ
чисел используется смешанная двоично-десятичная
«система счисления», где для хранения каждого
десятичного знака нужен полубайт (4 бита) и
десятичные цифры от 0 до 9 представляются
соответствующими двоичными числами от 0000 до
1001.
Например, упакованный десятичный формат,
предназначенный для хранения целых чисел с 18
значащими цифрами и занимающий в памяти 10 байт
(старший из которых знаковый), использует именно
этот вариант.
0000 0001 0010 0011
0
1
2
3

74.

Двоично-десятичное кодирование
Для хранения числовых значений в компьютере используется
двоичная запись, как боле экономная с точки зрения
использования памяти компьютера.
Пример:
Для хранения числа 99 требуется 2 байта ASCII кода. Если
использовать 2 байта для хранения двоичного числа, то диапазон
значений целых числе может быть от 0 до 2^16 = 65635 , что
является значительным усовершенствованием.
Тем не менее, для хранения целых чисел в компьютерах
используется другая система кодирования, называемая
представлением в дополнительном коде, которая дает
возможность кодирования положительных и отрицательных
чисел.
Для хранения не целых чисел используется другая форма –
представление чисел с плавающей точкой.

75.

Кодирование числовой информации.
Прямой и дополнительный код числа
Для представления чисел в памяти ПК используются
два формата:
формат с фиксированной точкой (запятой) целые
числа;
формат с плавающей точкой (запятой)
вещественные числа.
Для хранения положительных чисел используется
прямой код числа, для хранения значения
отрицательных чисел- дополнительный код

76.

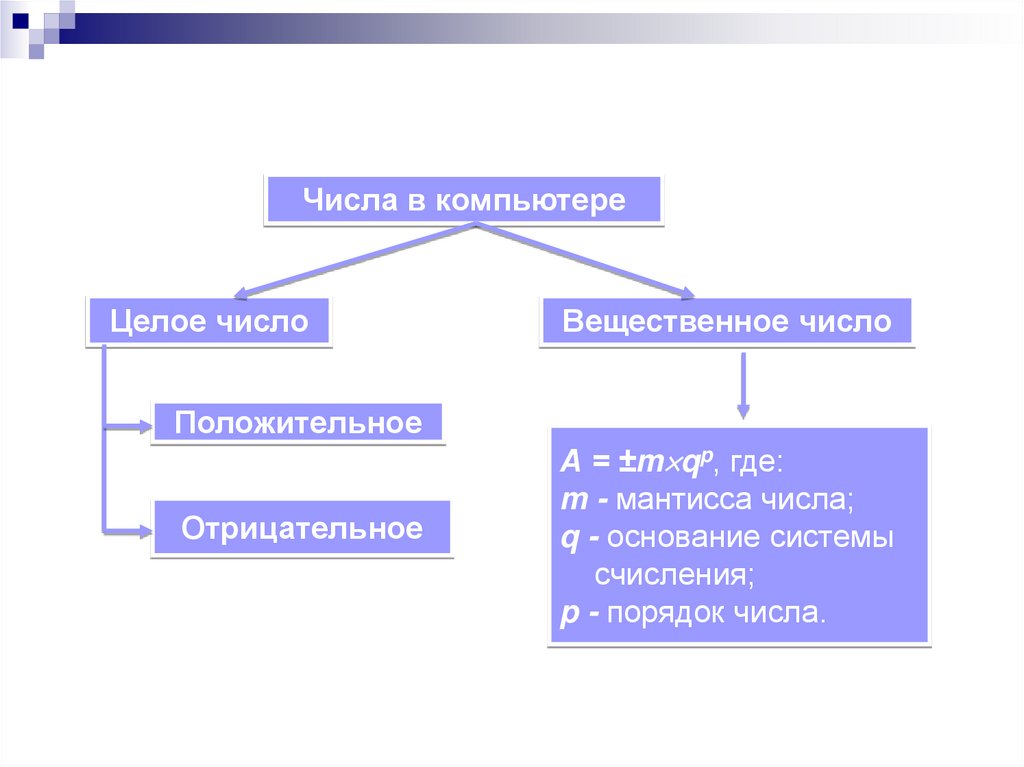
Числа в компьютере
Целое число
Положительное
Отрицательное
Вещественное число
А = ±m qp, где:
m - мантисса числа;
q - основание системы
счисления;
p - порядок числа.

77.

Числа со знаками и без них
Данные в памяти компьютер хранятся в виде двоичных
кодов, которые могут быть интерпретированы как числа
со знаками, так и без знаков.
В случае представления величины со знаком самый
левый (старший) разряд указывает на положительное
число, если содержит нуль, и на отрицательное, если —
единицу.
Вообще разряды нумеруются справа налево, начиная с 0.
Ниже показана нумерация бит в двухбайтовом машинном
слове

78.

Примеры позиционных систем счисления
Так же существуют позиционные системы с
отрицательными основаниями
(негапозиционные):
-2 — нега-двоичная система счисления
-10 — нега-десятичная система счисления
Иногда также рассматривают позиционные
системы с нецелочисленными основаниями:
2,71... = е — е-ричная система счисления с основанием,
равным числу Эйлера
(применяется в натуральных логарифмах)

79.

Прямой и дополнительный код
положительного числа
Прямой код целого числа может быть получен следующим
образом: число переводится в двоичную систему счисления, а
затем его двоичную запись слева дополняют таким количеством
незначащих нулей, сколько требует тип данных, к которому
принадлежит число.
Например, если число 3710= 1001012, объявлено величиной типа
Integer (2 байта), то его прямым кодом будет 0000 0000 0010
0101, а если величиной типа Long (4 байта), то его прямой код
будет 0000 0000 0000 0000 0000 0000 0010 0101.
Для более компактной записи чаще используют
шестнадцатеричный код. Полученные коды можно переписать
соответственно как 002516 и 0000002516.
Дополнительный код положительного числа совпадает с его
прямым кодом.

80.

Прямой и дополнительный код
отрицательного числа
Дополнительный код целого отрицательного числа может быть
получен по следующему алгоритму:
1) записать прямой код модуля числа;
2) инвертировать его (заменить единицы нулями, нули — единицами):
3) прибавить к инверсному коду единицу.
Например, запишем дополнительный код числа (-37), интерпретируя
его как величину типа Long (4 байта):
5) прямой код числа 37 есть
4)
0000 0000 0000 0000 0000 0000 0010 0101;
6) инверсный код
1111 1111 1111 1111 1111 1111 1101 1010;
7) дополнительный код
1111 1111 1111 1111 1111 1111 1101 1011 или FFFFFFDB(16).

81.

Алгоритм получения числа по его коду.
При получении числа по его дополнительному коду,
прежде всего, необходимо определить его знак.
Если число окажется положительным, то просто
перевести его код в десятичную систему счисления.
В случае отрицательного числа необходимо выполнить
следующий алгоритм:
1) вычесть из кода числа 1;
2) инвертировать код;
3) перевести в десятичную систему счисления.
4) полученное число записать со знаком минус.

82.

Пример: получение числа по его коду.
Примеры. Запишем числа, соответствующие
дополнительным кодам:
а) 0000 0000 0001 0111.
Поскольку в старшем разряде записан нуль, то результат
будет положительным. Это код числа 23;
б) 1111 1111 1100 0000. Здесь записан код
отрицательного числа.
Исполняем алгоритм:
1) 1111 1111 1100 0000 - 1= 1111 1111 1011 1111;
2) 0000 0000 0100 0000;
3) 0000 0000 0100 0000(2) = 64(10). Ответ: -64.

83.

Представление в памяти компьютера чисел
с плавающей точкой (дробных чисел).
Поскольку каждая позиция десятичного числа
отличается от соседней на степень числа 10, умножение
на 10 эквивалентно сдвигу десятичной запятой на
одну позицию вправо.
Аналогично деление на 10 сдвигает десятичную запятую
на позицию влево.
Поэтому :
,
,
,
120100000 = 1 201* 10^8 = 0 1201*10^9= 12 01*10^7...
Десятичная запятая «плавает» в числе и больше не
помечает абсолютное место между целой и дробной
частями, поэтому дробные числа называют
«числами с плавающей точкой».

84.

Данные (и программы) в памяти компьютера
хранятся в двоичном виде, т. е. в виде цепочек единиц и
нулей.
Представление данных в компьютере
дискретно.Дискретное множество состоит из
отделенных друг от друга элементов.
Множество представимых в памяти компьютера
величин ограничено и конечно.
МАТЕМАТИКА:множество целых чисел дискретно,
бесконечно, не ограничено
ИНФОРМАТИКА:множество целых чисел дискретно,
конечно, ограничено
86