Похожие презентации:
Логика. Часть 2
1. Логика, часть 2
2. Историческая справка
Логикой, как наукой занималисьследующие учёные:
3. Аристотель (384-322 г.г. до н.э.)
Он пытался найти ответ навопрос “Как мы рассуждаем”,
изучал правила мышления.
Аристотель впервые дал
систематическое изложение
логики. Он подверг анализу
человеческое мышление, его
формы – понятие, суждение,
умозаключение.
Так возникла
формальная логика.
4. Г.В. Лейбниц (1646-1716)
Основы математической, илисимволической, логики заложил
немецкий ученый и философ
Г.В. Лейбниц (1646-1716).
Он сделал попытку построить
первые логические исчисления,
считал, что можно заменить
простые рассуждения
действиями со знаками,
и привел соответствующие
правила.
5.
Алгебра логики – математическийаппарат, с помощью которого
записывают, упрощают и
преобразовывают логические
высказывания.
6.
В работах английскогоматематика Джорджа
Буля логика обрела
свой алфавит, свою
орфографию и
грамматику. Его
считают создателем
алгебры логики,
которую в его учесть
назвали «Булевой
алгеброй»
7. Семья Буля
Буль был женат на Мэри Эверест племяннице знаменитогогеографа Джорджа Эвереста, также
занимавшейся наукой и преподававшей.
Четыре их дочери снискали известность
как учёные: геометр Алисия, химик Люси,
или как члены учёных семей: Мэри, жена
математика и писателя Ч. Г. Хинтона,
и Маргарет, мать математика Дж. И.
Тейлора, а пятая дочь— Этель Лилиан
Войнич — прославилась как писатель.
Буль умер на пятидесятом году жизни
от воспаления лёгких.
8. Логическое умножение (КОНЪЮНКЦИЯ)
AB
F
1
1
1
1
0
0
0
1
0
0
0
0
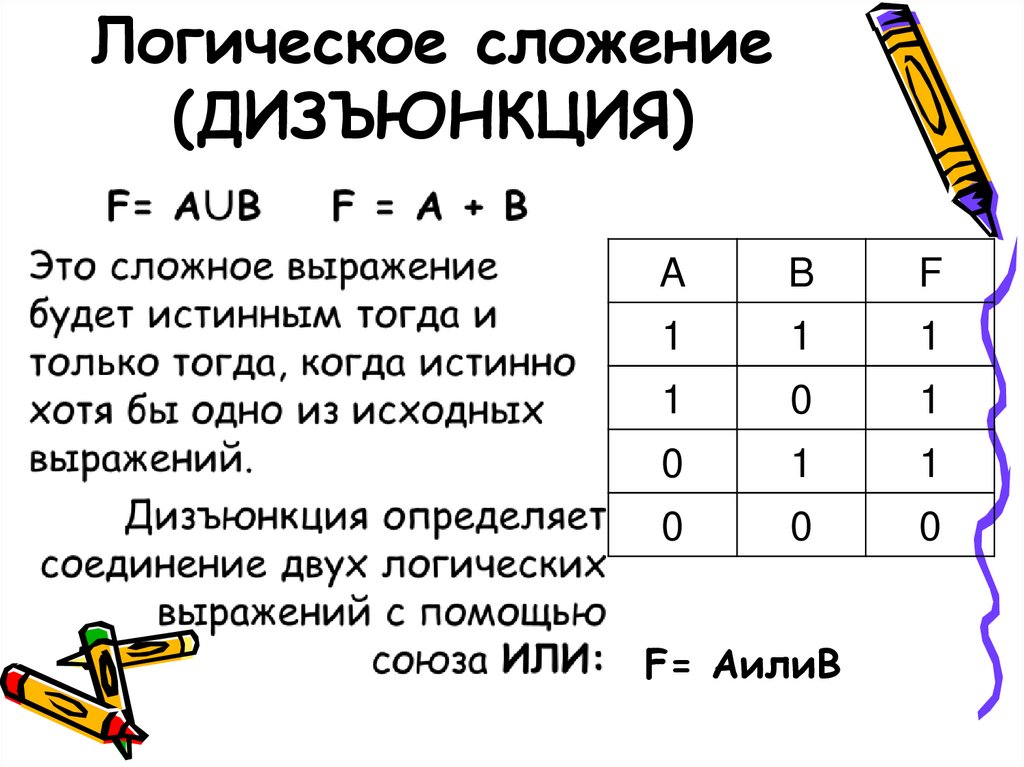
9. Логическое сложение (ДИЗЪЮНКЦИЯ)
AB
F
1
1
1
1
0
1
0
1
1
0
0
0
F= AилиB
10. Логическое отрицание (ИНВЕРСИЯ)
F=не А, F= А , F=А
Ели исходное выражение истинно, то результат
отрицания будет ложным, и наоборот, если исходное
выражение ложно, то результат отрицания будет
истинным. Данная операция означает, что к исходному
логическому выражению добавляется частица НЕ или
слова НЕВЕРНО, ЧТО
A
F
0
1
1
0
11. Логическое следование (ИМПЛИКАЦИЯ)
Связывает два простых логических выражения, изкоторых первое является условием (А), а второе
(В)– следствием из этого условия. Результатом
ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда
условие А истинно, а следствие В ложно.
Обозначается символом "следовательно" и
выражается словами ЕСЛИ … , ТО …
F A B
A
B
F
1
1
1
1
0
0
0
1
1
0
0
1
12. Логическая равнозначность (ЭКВИВАЛЕНТНОСТЬ)
F A BA
B
F
1
1
1
1
0
0
0
1
0
0
0
1
Определяет результат
сравнения двух простых
логических выражений А и В.
Результатом
ЭКВИВАЛЕНТНОСТИ является
новое логическое выражение,
которое будет истинным тогда
и только тогда, когда оба
исходных выражения
одновременно истинны или
ложны.
13. Порядок выполнения логических операций
1. инверсия2. конъюнкция
3. дизъюнкция
4. импликация
5. эквивалентность
Для изменения указанного порядка
выполнения операций используются скобки.
14. Законы логики
Перемест ит ельный (коммут ат ивный) закон:для логического сложения: А Ú B = B Ú A;
для логического умножения: A & B = B & A.
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти
высказывания
Сочет ат ельный (ассоциат ивный) закон:
для логического сложения: (А U B) U C = A
U(B UC);
для логического умножения: (A & B) & C = A & (B & C).
При одинаковых знаках скобки можно ставить произвольно или вообще опускать
Распределит ельный (дист рибут ивный) закон:
для логического сложения:(А U B) & C =(A & C) U(B & C);
для логического умножения:(A & B) U C=(AUC)&(B
U C).
Закон определяет правило выноса общего высказывания за скобку
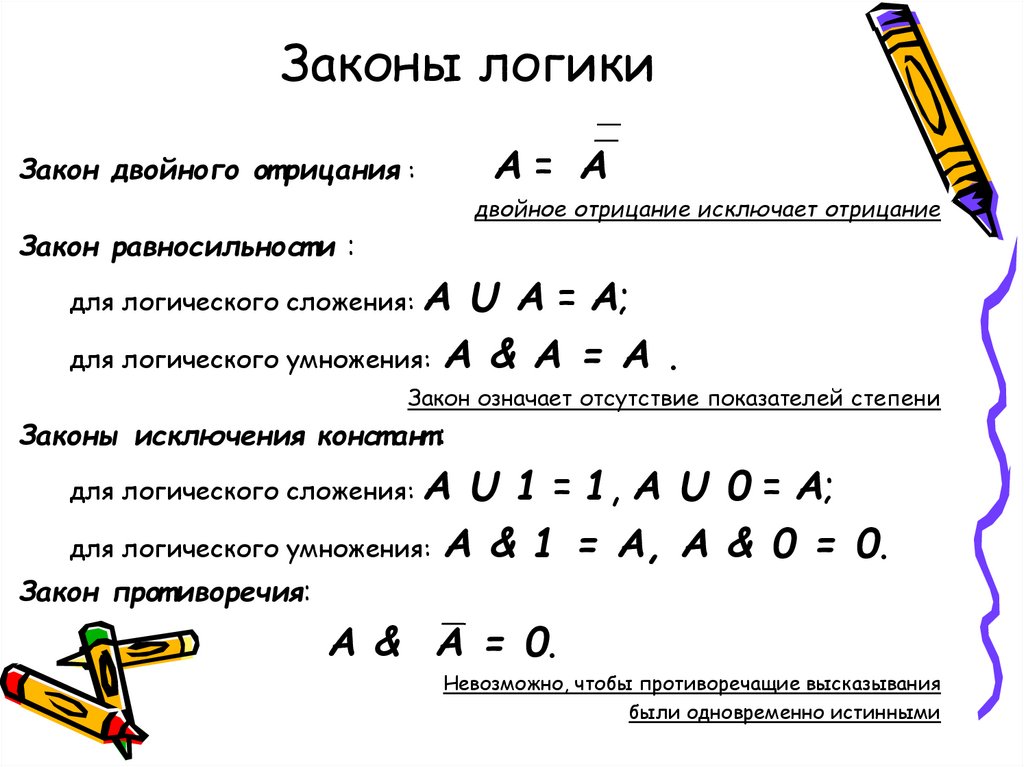
15. Законы логики
А= АЗакон двойного от рицания :
двойное отрицание исключает отрицание
Закон равносильност и :
для логического сложения: А U A = A;
для логического умножения: A & A = A .
Закон означает отсутствие показателей степени
Законы исключения конст ант :
для логического сложения: А U 1 = 1, А U 0 = A;
для логического умножения: A & 1 = A, A & 0 = 0.
Закон прот иворечия:
A & A = 0.
Невозможно, чтобы противоречащие высказывания
были одновременно истинными
16. Законы логики
Закон общей инверсии (законы де Моргана):для логического сложения: А Ú B
= A & B;
для логического умножения: A & B; = А U B
для логического отрицания: А
B = A & B;
А B = А U B
Закон исключения т рет ьего:
A U А= 1.
Из двух противоречащих высказываний об одном и том же предмете одно всегда
истинно, а второе — ложно, третьего не дано.
Закон поглощения:
для логического сложения: А U(A & B) = A;
для логического умножения: A & (A U B) = A.
17. Пример 1.
Упростить формулу (А U В) & (А U С).Решение:
Раскроем скобки: (А U В) & (А U С) = A & A U A & C U B &
A U B & C;
Так как A & A =A, следовательно,
A & A U A & C U B & A U B & C = A U A & C U B &
A U B & C;
В высказываниях А и А & C вынесем за скобки А и используя
свойство А U 1= 1, получим
A U A & C U B & A U B & C = A & (1 U C) U B &
A U B & C = A U B & A U B & C;
Аналогично предыдущему пункту вынесем за скобки
высказывание А.
A U B & A U B & C = A & (1 U B) U B & C = A U B
18.
Пример 9, стр. 57,задачник 1.
Упростить формулу (А U В) (В U С).
Решение:
Избавимся от отрицания импликации, так как А B = A & B,
то (А U В) (В U С) = (А U В) & (В U С) = (А U В) & (В U С) =
раскроем скобки = А & В U В & В U А & С U B & C = т .к. В & В
=В, т о = А & В U В U А & С U B & C = вынесем за скобки В =
В & (А U 1) U А & С U B & C = т .к. А U 1= 1, т о= В & 1 U А &
С U B & C = В & (1 U C) U А & С = В & 1 U А & С =
В U А & С
19. Домашнее задние Задачник 1, стр. 58, №34
Для удобства решения знак U можнозаменить на +, а знак & на *.
Тогда выражение будет иметь вид:
X+(X+Y)+Y*(X*Y))
Выполнить в тетради

















 Математика
Математика Философия
Философия








