Лекция 1. Особенности геологических образований и процессов как объектов математического моделирования

1. Математические методы моделирования в геологии

Лекция 1
Особенности геологических
образований и процессов как
объектов математического
моделирования. Типы моделей и
принципы геолого-математического
моделирования
Хасанова Гульнара Бариевна

2. Литература:

1.
Каждан
А.Б.,
Гуськов
О.И.
Математические методы в геологии. Учебник
для ВУЗов.- М.: Недра, 1990.
2. Мягков В.Ф. Геохимический метод
парагенетического анализа руд.- М.: Недра,
1984.- 126 с.
3. Поротов Г.С. Математические методы
моделирования в геологии: Учебник.- СПб.:
Санкт-Петербургский
горный
институт,
2006.- 223 с.
4. Шестаков Ю.Г. Математические методы в
геологии. Учебное пособие.- Красноярск.
Изд-во ун-та, 1988.

3.

Особенности геологических процессов и образований,
определяющие методы их изучения:
1. Представляют собой совокупность физических, химических и
биологических природных явлений, между которыми существуют
сложные причинно-следственные связи, поэтому свойства геологических
образований зависят от множества факторов, характеризуются сильной
изменчивостью, а сами объекты имеют весьма сложное строение.
2. Геологические процессы
длительны, а геологические
образования
имеют
значительные
размеры
и
скрыты в недрах, что исключает
возможность
их
полного
всестороннего изучения путем
непосредственного наблюдения.

4.

Особенности геологических процессов и образований,
определяющие методы их изучения:
Отмеченные особенности геологических объектов обуславливают необходимость
применения выборочного метода измерения. В выборочном методе
используются понятия - генеральная и выборочная (или выборка)
совокупность.
Исследованию подвергается выборка, а выводы распространяются на
генеральную совокупность.
Основным методом изучения плохо организованных систем, к которым относятся
геологические процессы и явления является моделирование, когда
непосредственный объект наблюдения заменяется его упрощенным аналогом –
моделью.
Генеральная совокупность включает в себя все
множество однопорядковых геологических объектов, а
выборочная совокупность – часть объектов, отбираемых
из генеральной совокупности по определенным правилам.

5.

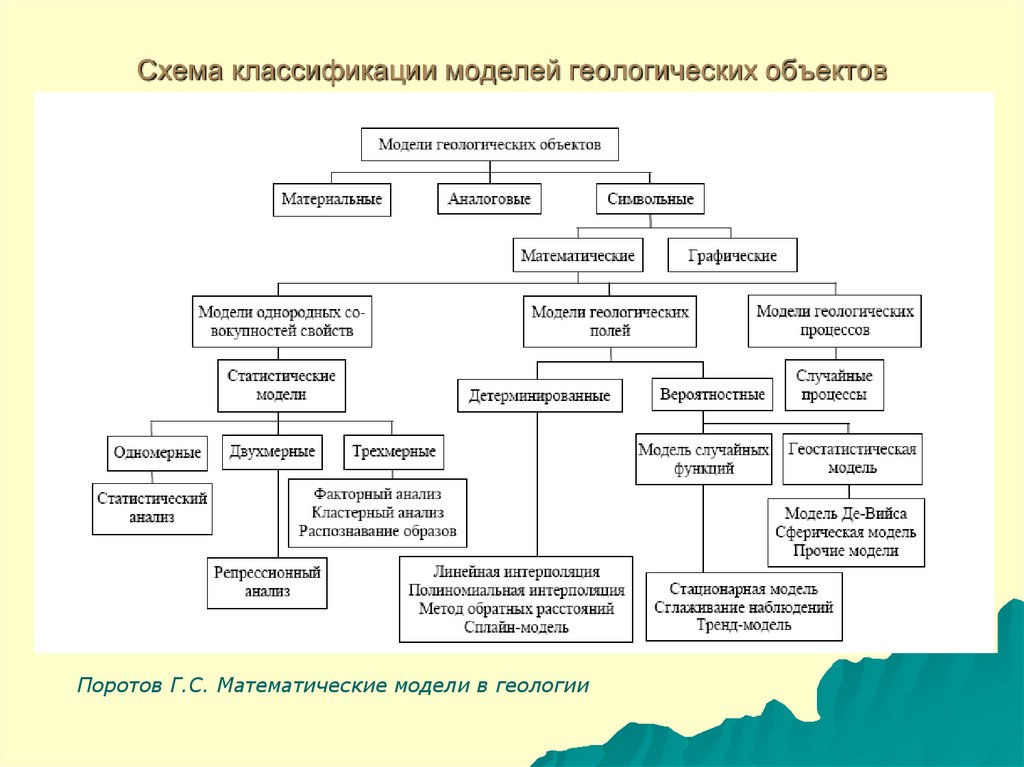
6. Схема классификации моделей геологических объектов

Поротов Г.С. Математические модели в геологии

7. Этапы геолого-математического моделирования

1) формулировка геологической задачи;
2) определение геологической совокупности, т.е. установление границ
геологического объекта или временного интервала геологического
процесса;
3) выявление главных свойств объекта или параметров процесса в
рамках поставленной задачи;
4) переход от геологической совокупности к опробуемой и выборочной с
учетом особенностей методов исследования;
5) выбор типа математической модели;
6) формулировка математической задачи в рамках выбранной
математической модели;
7) решение математической задачи на основе вычисления параметров
математической модели объекта;
8) интерпретация полученных результатов применительно к
геологической задаче;
10) оценка вероятности и величины возможной ошибки за счет
неадекватности модели и объекта.

8.

Математическая статистика.
Математическая
статистика
-
это
прикладная
математическая
дисциплина, которая занимается изучением закономерностей в массовых,
случайных, однородных, повторяющихся объектах и явлениях природы,
техники и общественной жизни.
Предметом исследования математической статистики является
статистическая совокупность. Статистическая совокупность – это
такое множество, которое состоит из массы однородных, случайных,
повторяющихся объектов или явлений, обладающих качественной
общностью.

9. Требования, предъявляемые к выборочной совокупности

1. Условие массовости вызвано тем, что статистические
закономерности проявляются лишь в массовых явлениях,
поэтому объем выборочной совокупности должен быть
достаточно большим. Эмпирическим путем установлено, что
надежность статистических оценок резко снижается при
уменьшении объема выборки в диапазоне от 60 до 30-20
значений, а при меньшем количестве наблюдений применять
статистические методы не имеет смысла.
2. Условие однородности заключается в том, что выборочная
совокупность должна состоять из наблюдений принадлежащих
одному объекту и выполненных одинаковым способом, т.е. при
постоянном размере проб и методе анализа или измерения.

10. Требования, предъявляемые к выборочной совокупности

3. Условие случайности предусматривает непредсказуемость
результата единичного выборочного наблюдения. Сложность и
изменчивость геологических объектов как правило, исключает
возможность точной оценки их свойств до проведения
наблюдений. Но условие случайности строго выполняется
только тогда, когда расположение мест отбора проб или
проведения замеров вообще не будет связано с величиной,
характеризующей его свойства. В практике ГРР это достигается
опробованием по сети наблюдений, которая намечается
заранее.
4. Условие независимости предполагает, что результаты
каждого наблюдения не зависят от результатов предыдущих и
последующих наблюдений, а при проведении наблюдений на
площади или в объеме результаты не зависят от координат
пространства.

11. В геологической практике применяют 4 шкалы измерений:

Номинальная шкала основана на классификации наблюдений во
взаимно исключающие друг друга категории одинакового типа. эти
категории могут быть обозначены цветами: красный, черный, зеленый и
т.д; символами: «А», «В», «С» и т.д.; числами: «1», «2», «3» и т.д.
примером может служить классификация ископаемых остатков:
брахиоподы, криноидеи и т.д.
Порядковая шкала применяется в тех случаях, когда изучаемые
объекты можно расположить в некотором порядке в зависимости от
изменения какого-либо свойства, однако разницу в изменении нельзя
оценить количественно. Пример – шкала твердости Мооса, твердость
минералов имеет девять значений и возрастает с повышением ранга от 1
до 10. Аналогично метаморфические породы можно ранжировать по
степени метаморфизма.
Интервальная шкала – это шкала в которой интервалы перехода от
одного класса объектов к другому равны, но не указана точка
абсолютного 0. Например, температурная шкала с различными точками
нулей – по Цельсию, Фарингейту и т.д.
Относительная шкала имеет одинаковые приращения между
отдельными градациями и точку абсолютного нуля. Числами
относительной шкалы характеризуются замеры мощностей рудных тел,
результаты химических анализов и др. свойства объектов которые могут
быть оценены количественно.