Эллипс. Гипербола. Парабола Изучение нового материала. Контрольная работа. Урок геометрии в 10 классе

1.

Урок
геометрии в 10 классе
Урок вывешен на сайте:
http://pavls1954.wixsite.com/1712

2.

Приветствую вас на уроке
Девиз урока
Малый человек и на горе мал;
исполин велик и в яме.
М.В.Ломоносов.
Успешного усвоения учебного материала

3.

КР
Тема урока:
Эллипс. Гипербола. Парабола
Изучение нового материала

4.

Цели урока:
- Рассмотреть некоторые сведения
из планиметрии.
- Проверить знание основных теорем
и формул площади треугольника.
- Продолжить формирование
культуры устной и письменной
математической речи и культуры
общения, умения работать в паре и
группе.

5.

Памятка для учащихся:
- Цени полученные знания.
- Продемонстрируй грамотность в
выполнении поставленных задач.
-Воспринимай задания с интересом,
вдумчиво.
-Не бойся ошибаться.
- Поверь в свои силы!
- Будь в хорошем настроении!

6.

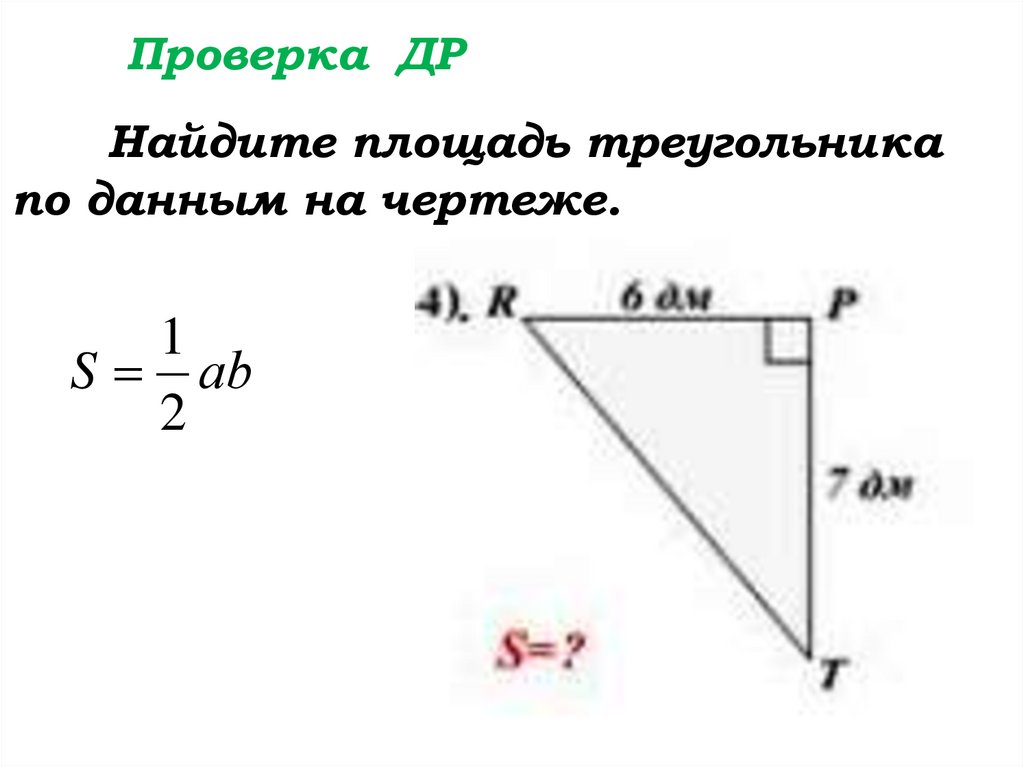
Проверка ДР
Найдите площадь треугольника
по данным на чертеже.
1
S аb
2

7.

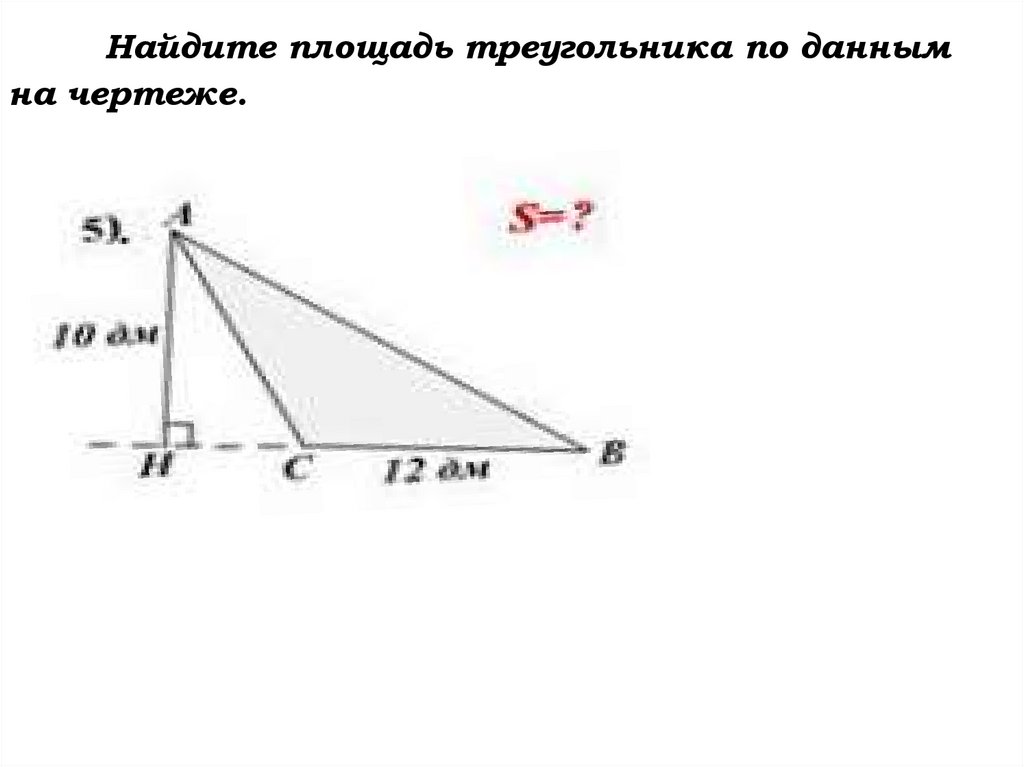
Найдите площадь треугольника по данным
на чертеже.

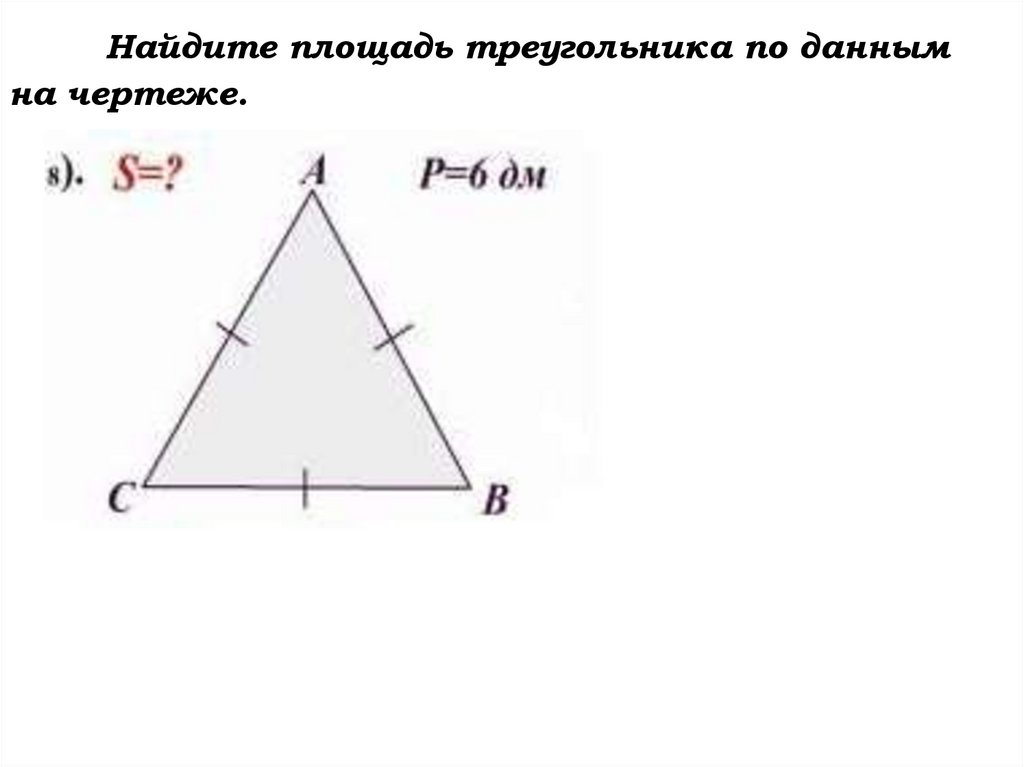
8.

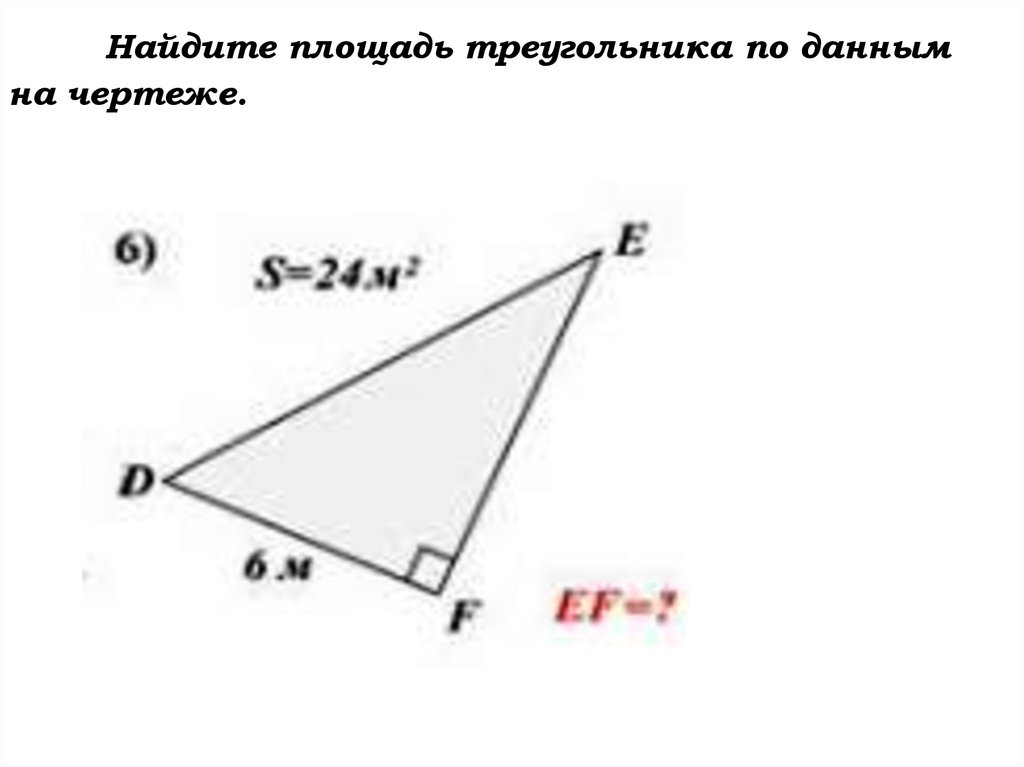
Найдите площадь треугольника по данным
на чертеже.

9.

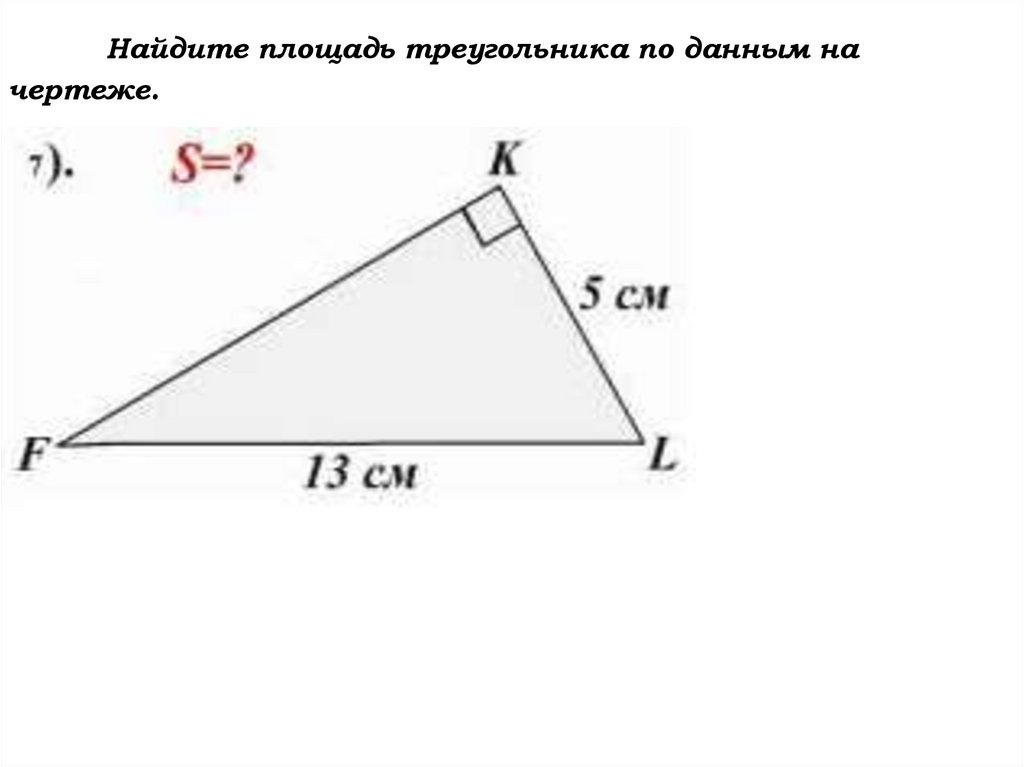
Найдите площадь треугольника по данным на
чертеже.

10.

Найдите площадь треугольника по данным
на чертеже.

11.

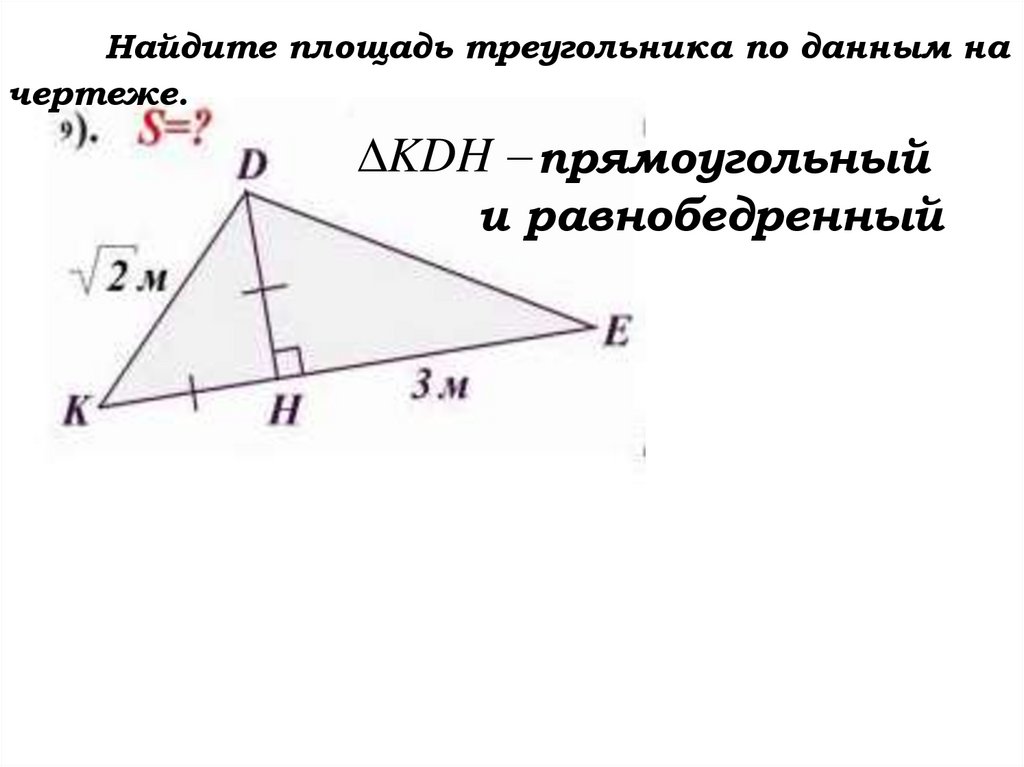
Найдите площадь треугольника по данным на
чертеже.
KDH прямоугольный
и равнобедренный

12.

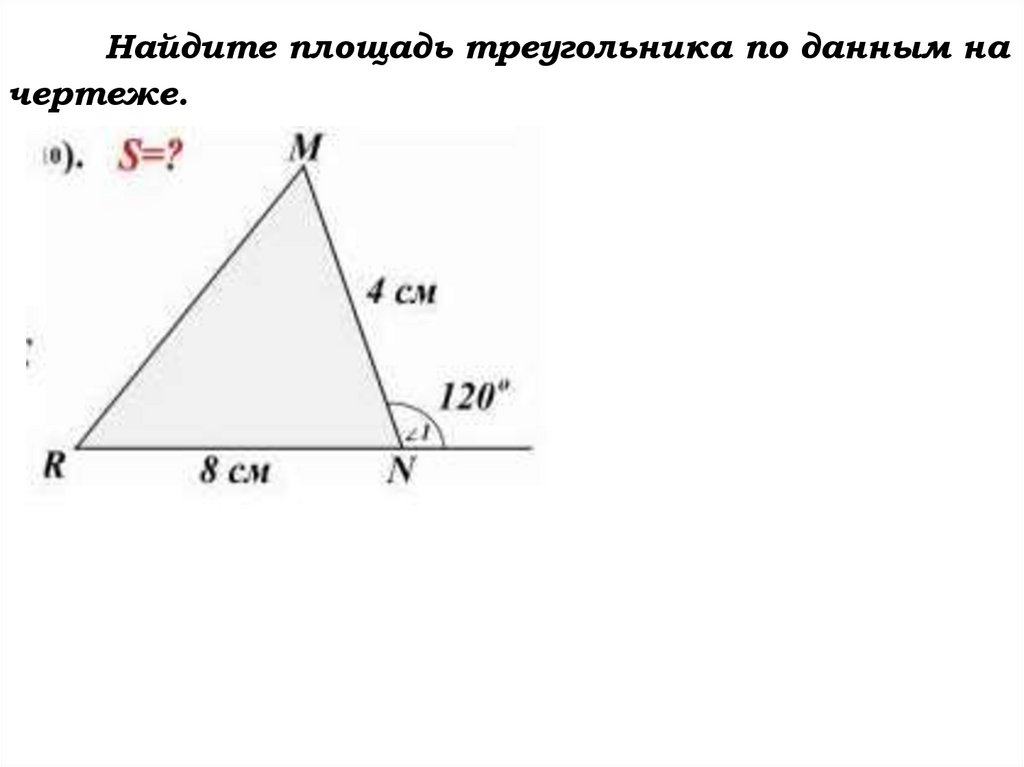
Найдите площадь треугольника по данным на
чертеже.

13.

Повторяем уравнение окружности

14.

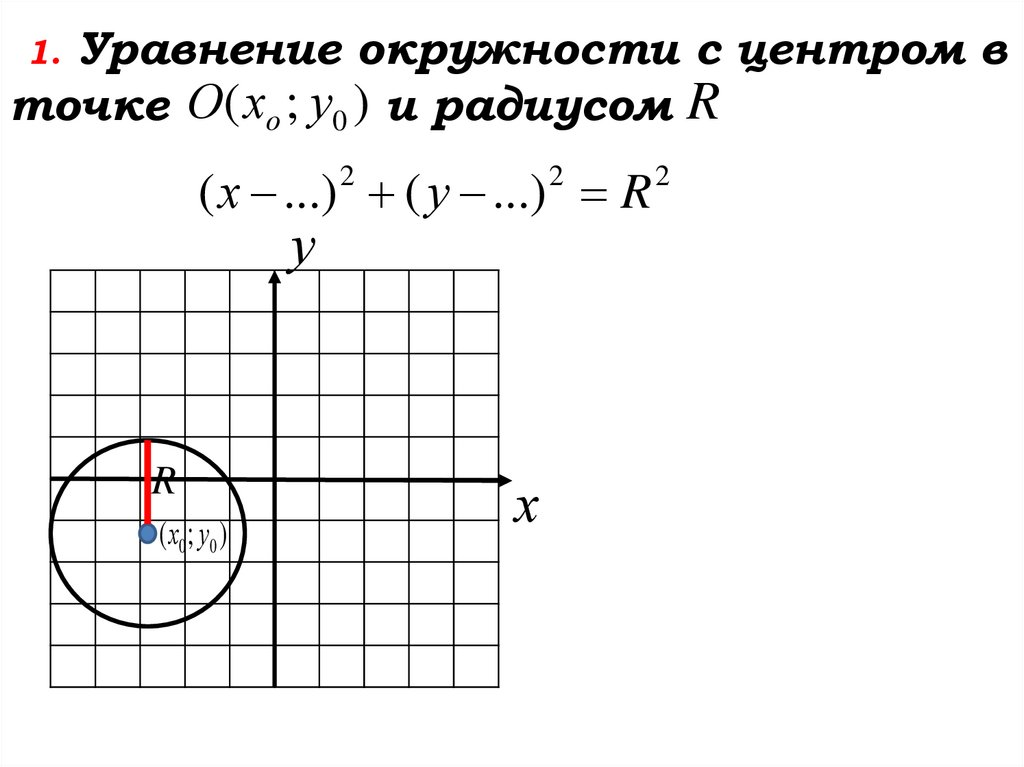
1. Уравнение окружности с центром в
точке О( хо ; у0 ) и радиусом R
( х ...) ( у ...) R
2
2
у
R
( х0 ; у0 )
х
2

15.

1. Уравнение окружности с центром в
точке О( хо ; у0 ) и радиусом R
( х хо ) ( у у0 ) R
2
2
2
А).Запишите уравнение окружности
с центром в точке О(0;0) и
радиусом, равным 3.

16.

1. Уравнение окружности с центром
в точке О( хо ; у0 ) и радиусом R
( х хо ) ( у у0 ) R
2
2
2
А).Запишите уравнение окружности
с центром в точке О (0;0) и
радиусом, равным 3.
х у 9
2
2
Б).Запишите уравнение окружности
с центром в точке О ( 2; 3) и
радиусом, равным 1.

17.

1. Уравнение окружности с центром в
точке О ( хо ; у0 ) и радиусом R
( х хо ) ( у у0 ) R
2
2
2
А).Запишите уравнение окружности с
центром в точке О (0;0) и радиусом,
равным 3.
2
2
х у 9
Б).Запишите уравнение окружности с
центром в точке О ( 2; 3)и радиусом,
равным 1.
( х 2) ( у 3) 1
2
2

18.

1. Уравнение окружности с центром в
точке О ( хо ; у0 ) и радиусом R
( х хо ) ( у у0 ) R
2
2
2
В) Укажите координаты центра
окружности и её радиус:
а)( х 3) ( у 2) 4
О(...;...); R ...
2
б )( х 1) ( у 2) 16
О(...;...); R ...
в ) х ( у 4) 7
О(...;...); R ...
2
2
2
2
2
Проверка

19.

1. Уравнение окружности с центром в
точке О ( хо ; у0 ) и радиусом R
( х хо ) ( у у0 ) R
2
2
В) Укажите координаты центра
её радиус:
2
окружности и
а)( х 3) ( у 2) 4
О (3;2); R 2
б )( х 1) ( у 2) 16
О( 1; 2); R 4
в ) х ( у 4) 7
О(0; 4); R 7
2
2
2
2
2
2

20.

1. Уравнение окружности с центром в
точке О ( хо ; у0 ) и радиусом R
( х хо ) ( у у0 ) R
2
2
В) Укажите координаты центра
её радиус:
2
окружности и
а)( х 3) ( у 2) 4
О (3;2); R 2
2
б )( х 1) ( у 2) 16
О( 1; 2); R 4
в ) х ( у 4) 7
О(0; 4); R 7
2
2
2
2
2

21.

2. Уравнение эллипса.
Эллипсом называется множество всех
таких точек плоскости, для которых
сумма расстояний до двух фиксированных
точек постоянна.
Фиксированные точки
называются фокусами
F1 F2 2c; F1М МF2 2а

22.

2. Уравнение эллипса.
Эллипсом называется множество всех
таких точек плоскости, для которых
сумма расстояний до двух фиксированных
точек постоянна.
Фиксированные точки
называются фокусами
F1 F2 2c; F1М МF2 2а
b
х
y
2 1
2
а
b
2
а
а
b
2
Каноническое уравнение
эллипса
b2 a2 c2 а2

23.

2. Уравнение эллипса.
F1 F2 2c; F1М МF2 2а
х
y
2
2
2
2
2 1; b a c а
2
а
b
2
2
Каноническое уравнение
эллипса
b
а
а
Начертите эллипс, который
задан уравнением:
х
y
1
16 9
2
b
2

24.

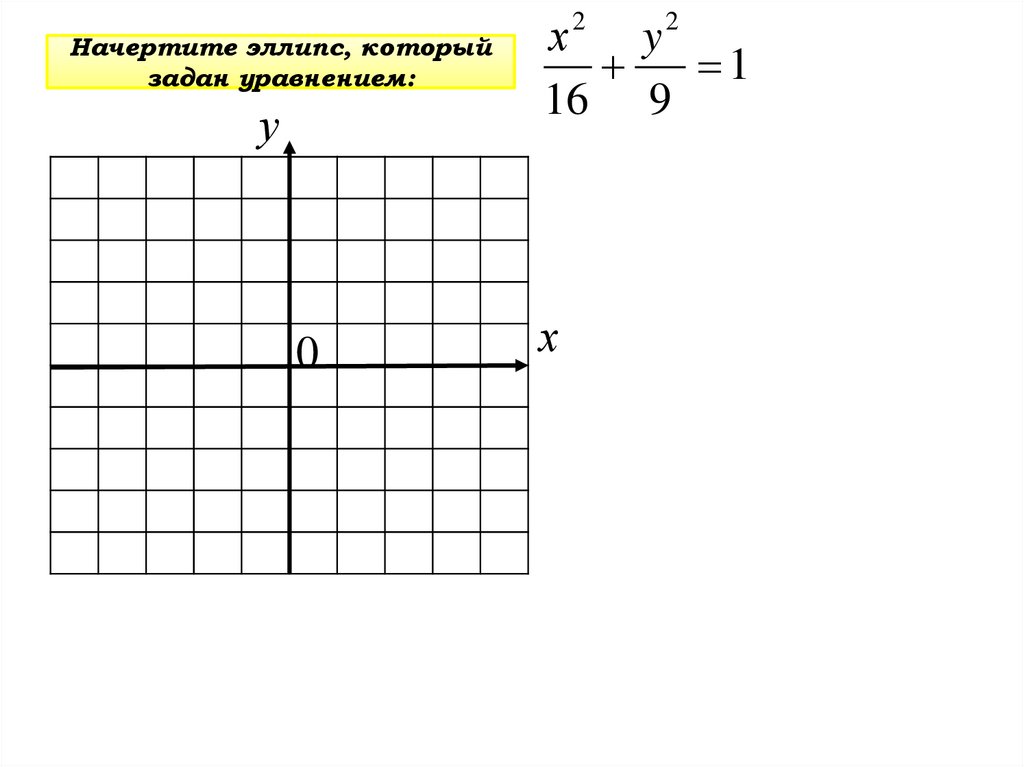
Начертите эллипс, который
задан уравнением:
у
0
х
y
1
16 9
2
х
2

25.

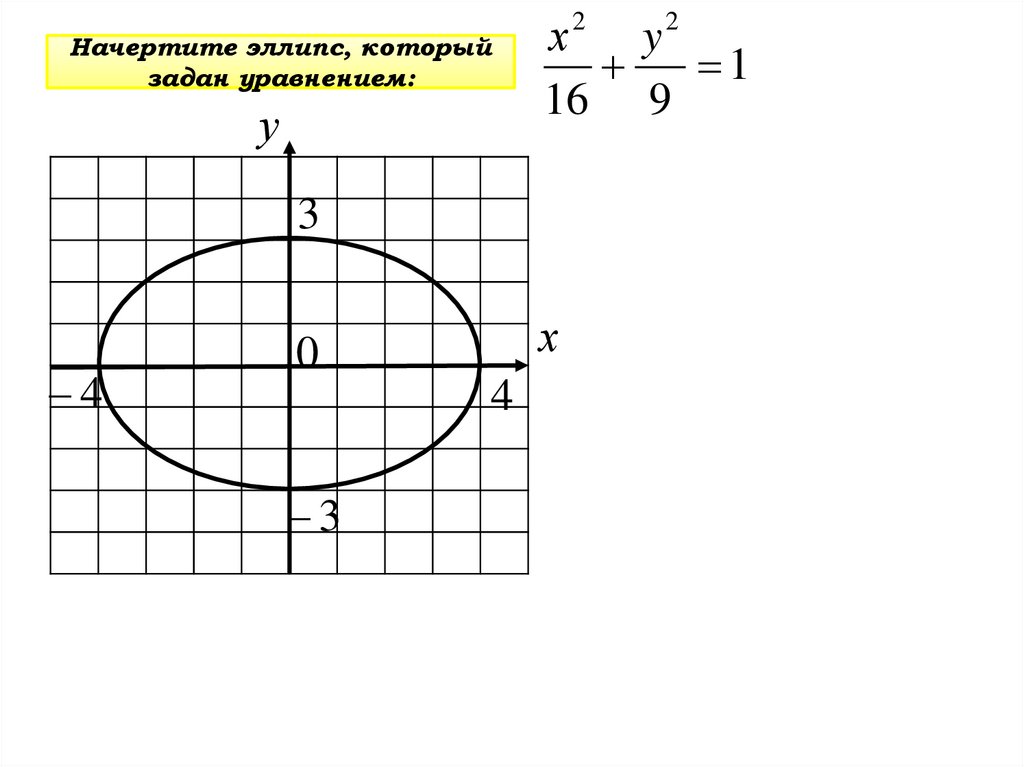
Начертите эллипс, который
задан уравнением:
у
х
y
1
16 9
2
3
4
х
0
4
3
2

26.

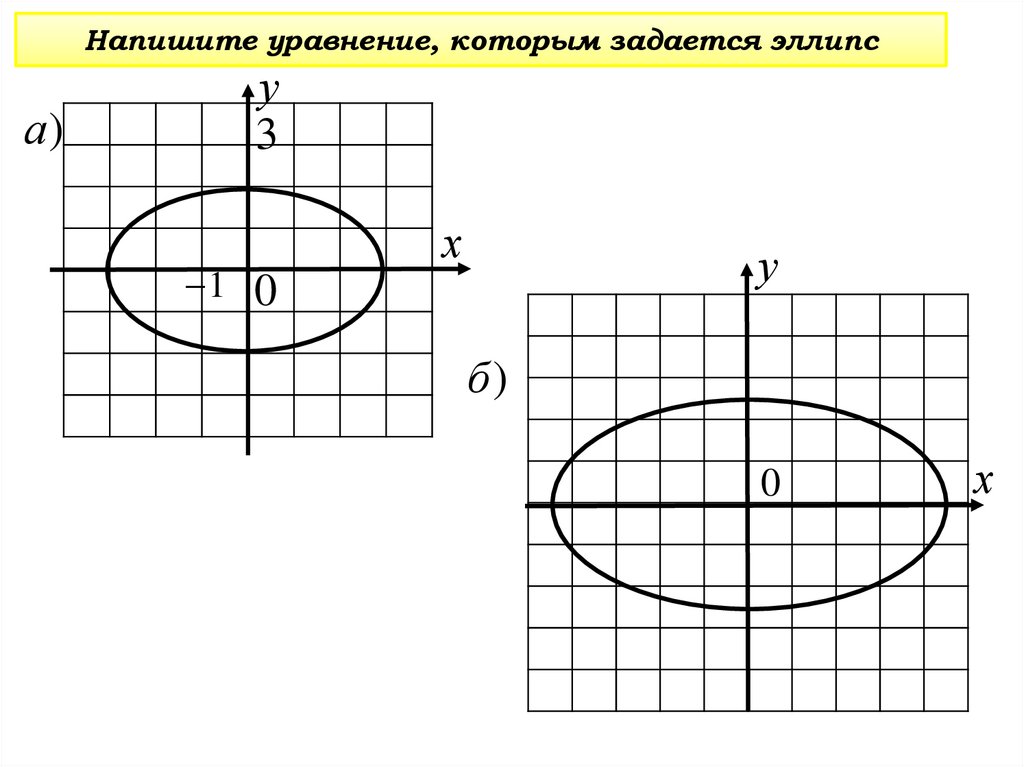
Напишите уравнение, которым задается эллипс
у
3
а)
1
х
у
0
б)
0
х

27.

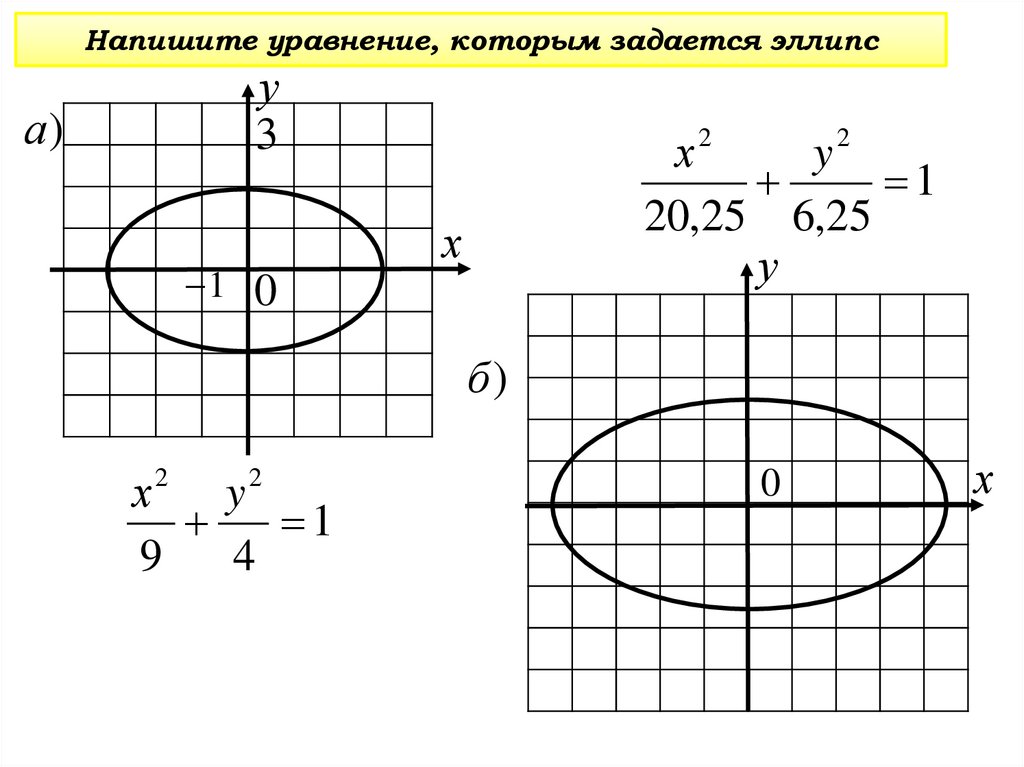
Напишите уравнение, которым задается эллипс
у
3
а)
1
х
y
1
20,25 6,25
у
2
х
0
2
б)
х
y
1
9
4
2
2
0
х

28.

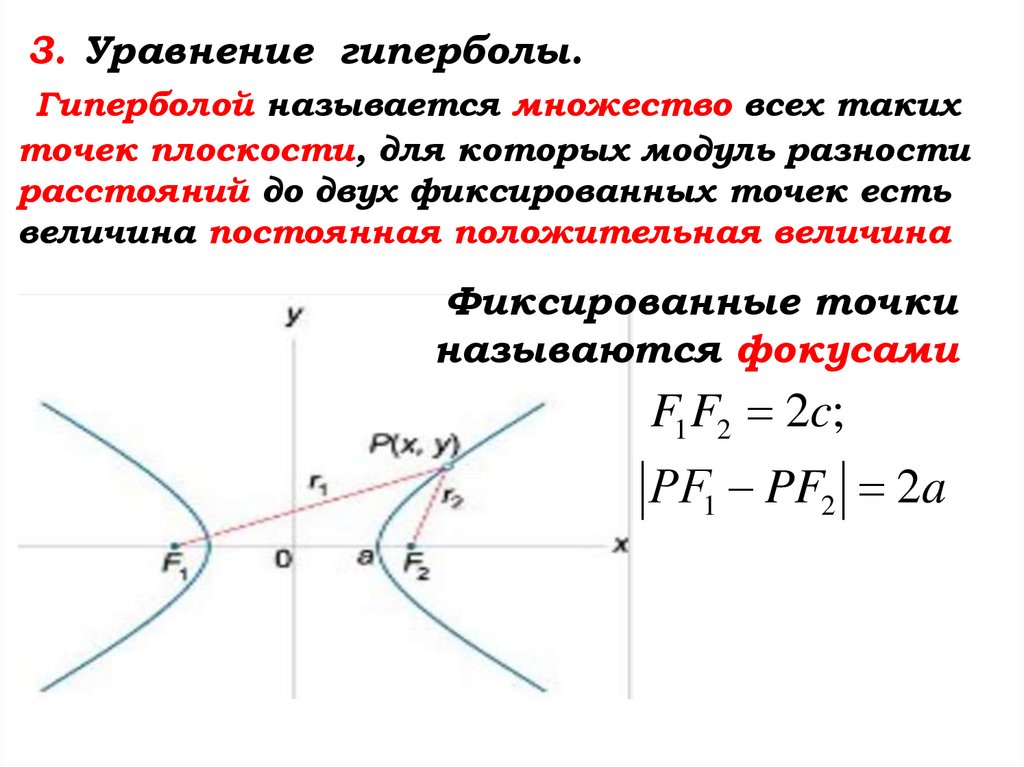
3. Уравнение гиперболы.
Гиперболой называется множество всех таких
точек плоскости, для которых модуль разности
расстояний до двух фиксированных точек есть
величина постоянная положительная величина
Фиксированные точки
называются фокусами
F1 F2 2c;
РF1 PF2 2a

29.

3. Уравнение гиперболы.
Гиперболой называется множество всех таких
точек плоскости, для которых модуль разности
расстояний до двух фиксированных точек есть
величина постоянная положительная величина
Фиксированные точки
называются фокусами
F1 F2 2c; РF1 PF2 2a
х
y
2 1
2
а
b
2
2
Каноническое уравнение
гиперболы
b c a
2
2
2

30.

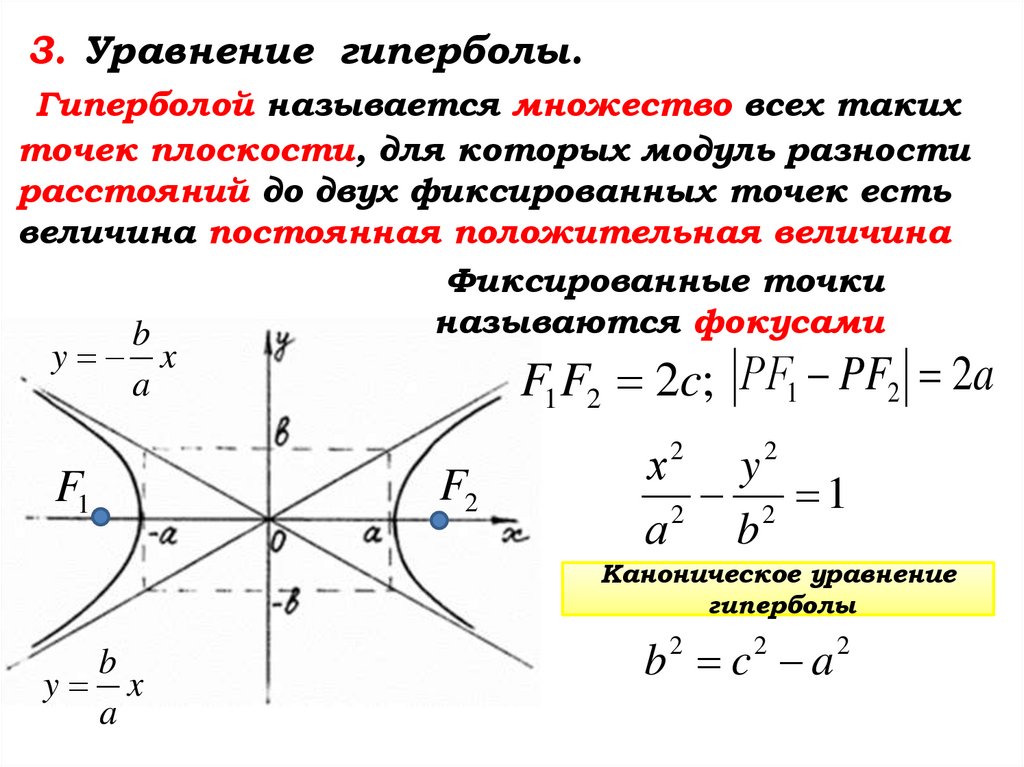
3. Уравнение гиперболы.
Гиперболой называется множество всех таких
точек плоскости, для которых модуль разности
расстояний до двух фиксированных точек есть
величина постоянная положительная величина
Фиксированные точки
называются фокусами
b
y x
a
F1 F2 2c; РF1 PF2 2a
х
y
2 1
2
а
b
2
F1
F2
2
Каноническое уравнение
гиперболы
b
y x
a
b c a
2
2
2

31.

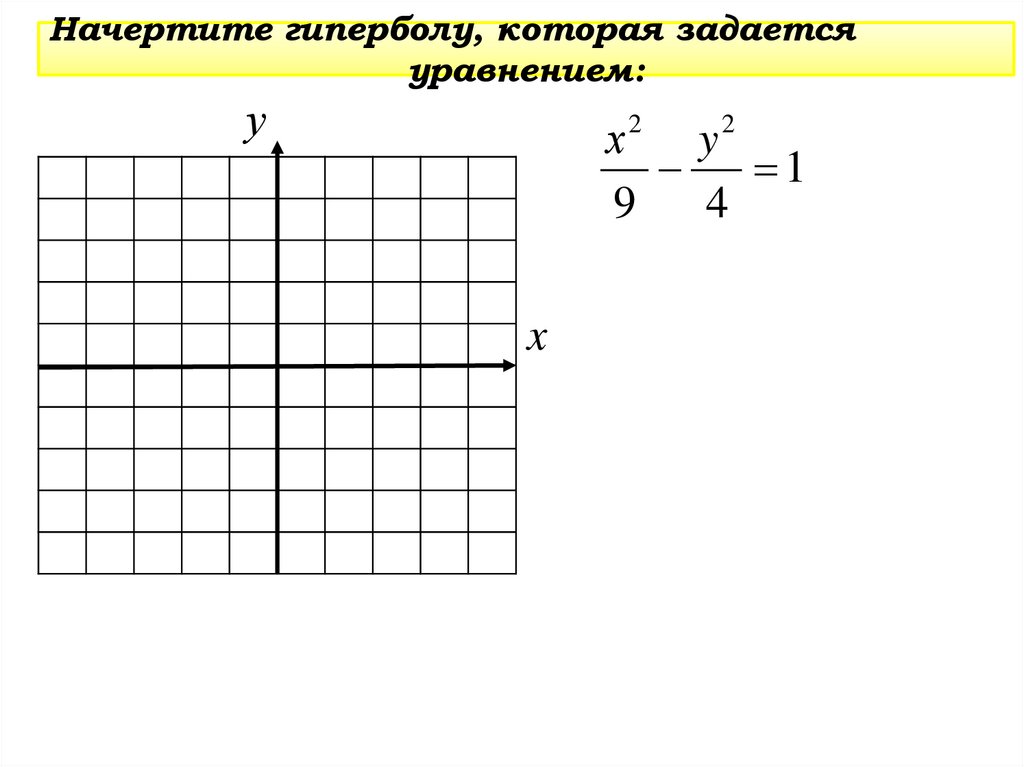
Начертите гиперболу, которая задается
уравнением:
у
х
y
1
9
4
2
x
2

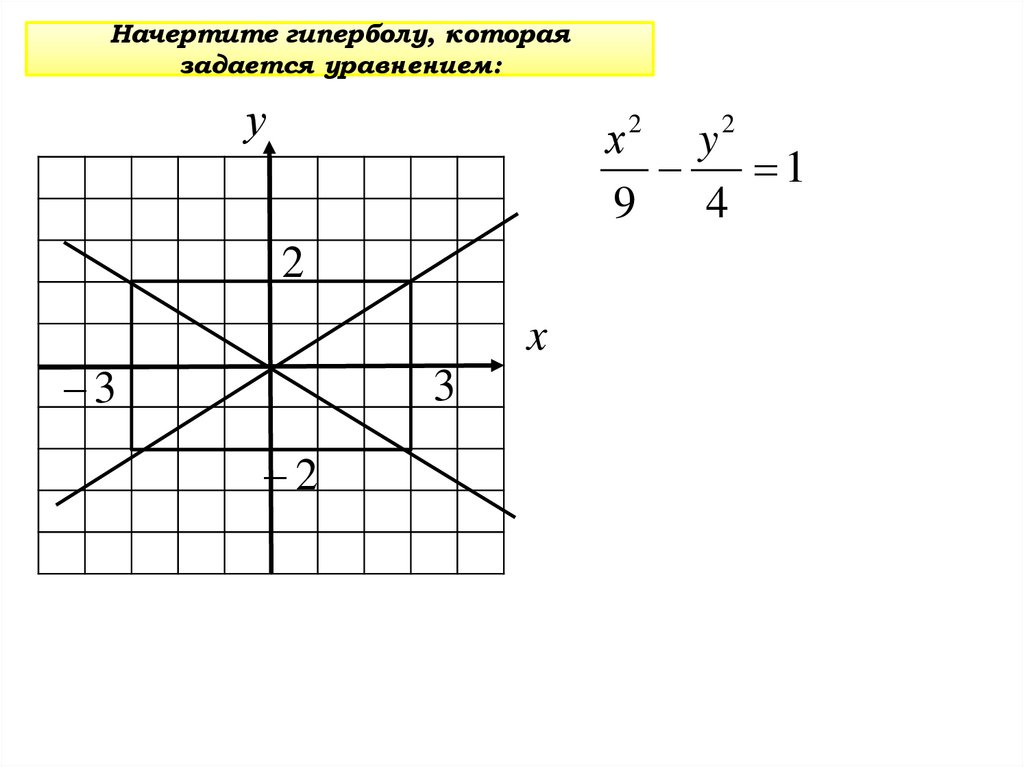
32.

Начертите гиперболу, которая
задается уравнением:
у
х
y
1
9
4
2
x
2

33.

Начертите гиперболу, которая
задается уравнением:
у
х
y
1
9
4
2
2
x
3
3
2
2

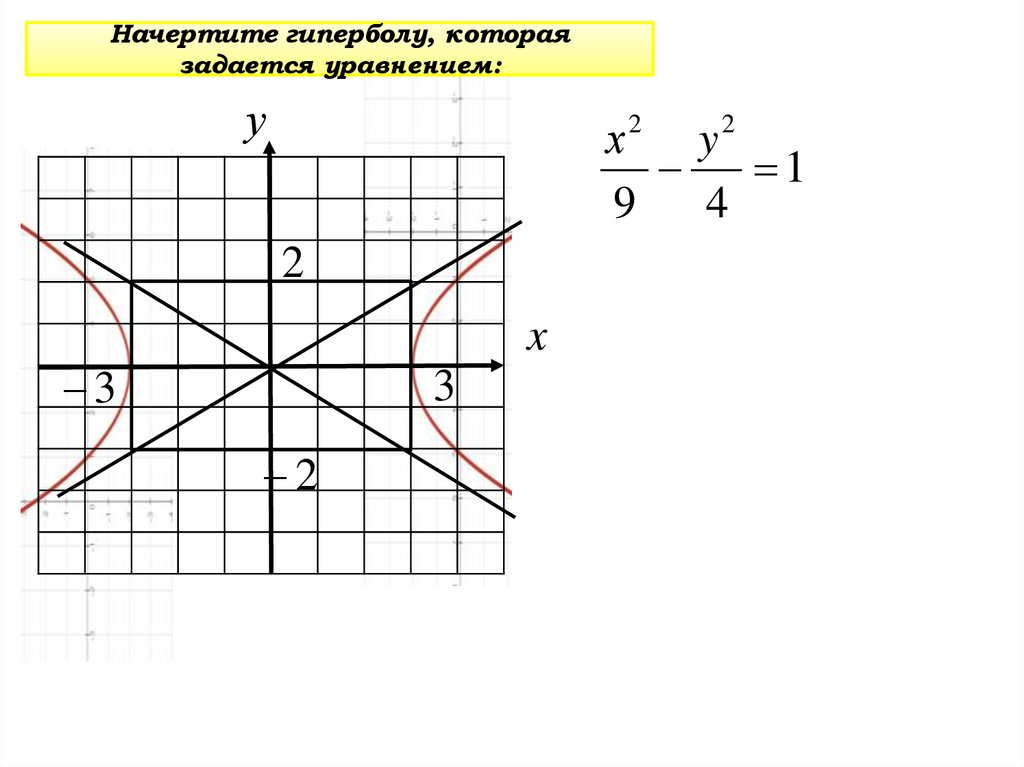
34.

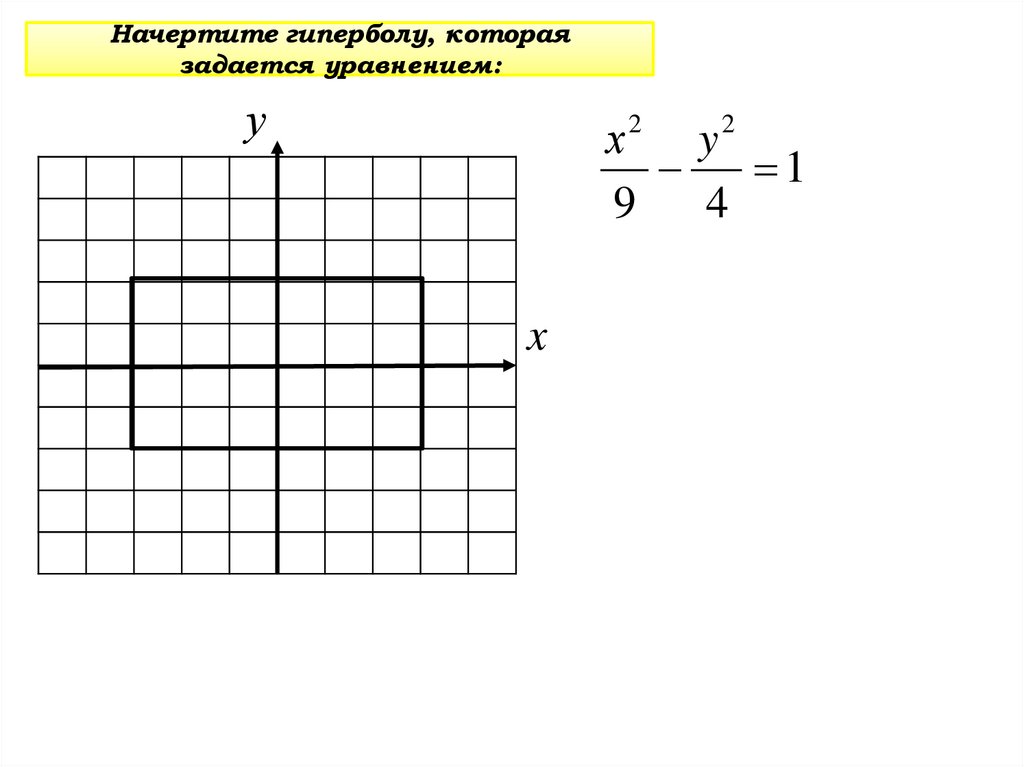
Начертите гиперболу, которая
задается уравнением:
у
х
y
1
9
4
2
2
x
3
3
2
2

35.

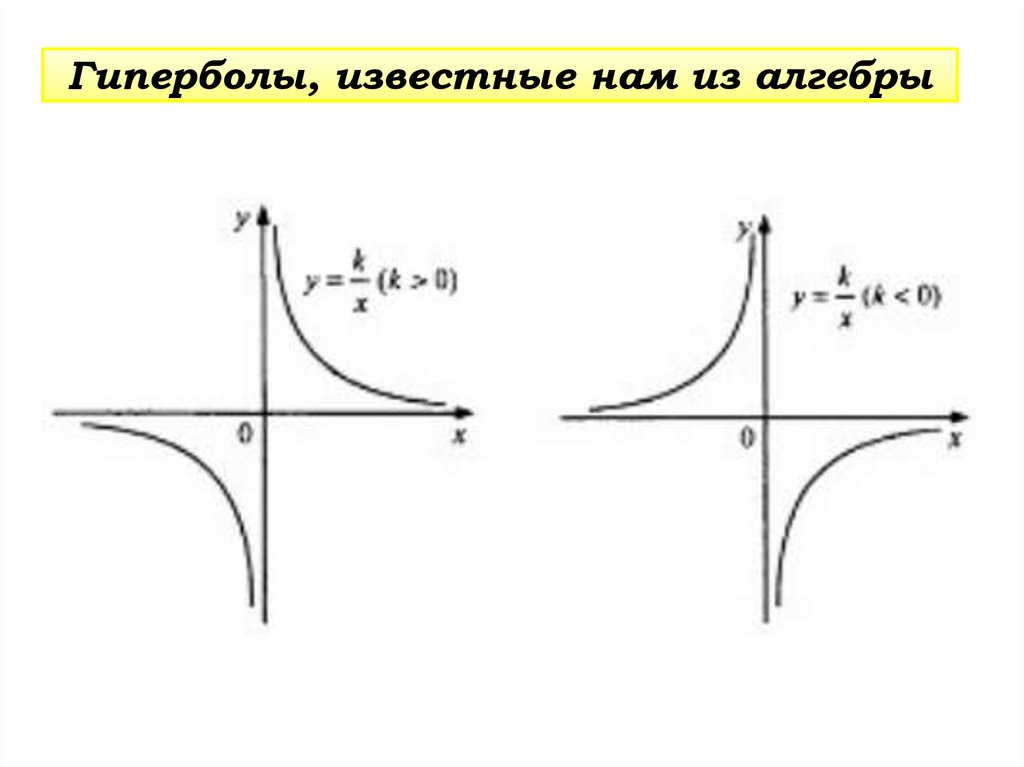
Гиперболы, известные нам из алгебры

36.

4. Уравнение параболы.
Параболой называется множество всех таких
точек плоскости, для которых расстояние до
фиксированной точки равно расстоянию до
фиксированной прямой, не проходящей через эту
точку

37.

4. Уравнение параболы.
Параболой называется множество всех таких
точек плоскости, для которых расстояние до
фиксированной точки равно расстоянию до
фиксированной прямой, не проходящей через эту
точку
Фиксированная точка
называется фокусом.
Фиксированная прямая
называется директрисой
y 2 2 px
Каноническое уравнение
параболы

38.

Дополнительная задача
Найдите площадь
треугольника, если его высоты
равны 3см, 4см и 6см.
Прочитайте задачу.
Запишите текст задачи в тетрадь.
Нужен ли в задаче чертёж?
Какая формула связывает площадь
и высоту треугольника.
Запишите эту формулу для трёх
случаев

39.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см.
Решение:
1
S aha
2
1
S bhb
2
1
S сhс
2
Назовите и запишите формулу
площади треугольника, которая
связывает наибольшее число входящих в
первые три формулы элементов.

40.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см.
Решение:
1
S aha
2
S
1
S bhb
2
1
S сhс
2
p( p a)( p b)( p c)
(*)
(**)
Что нужно выразить из формул (*),
чтобы использовать формулу (**), что
нужно дополнительно выразить?

41.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см.
Решение:
1
S aha
2
1
S bhb
2
1
S сhс
2
S
p( p a)( p b)( p c)
2S
а
ha
2S
b
hb
(*)
(**)
2S
с
hс
Замените некоторые буквы в последних
равенствах данными задачи

42.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см.
Решение:
1
S aha
2
1
S bhb
2
1
S сhс
2
(*)
2S
а
ha
2S
b
hb
(**)
2S
с
hс
2S
а
3
2S S
b
4
2
2S S
с
6
3
S
p( p a)( p b)( p c)
Что ещё выражаем, чтобы
использовать формулу (**) ?

43.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см. Решение:
1
1
1
(*
S
сhс
S bhb
S aha
2
2
2
S
p( p a)( p b)( p c)
2S
а
ha
2S
а
3
p ...
p a ...
p b ...
p c ...
2S
b
hb
2S S
b
4
2
)
(**)
2S
с
hс
2S S
с
6
3

44.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см. Решение:
1
1
1
(*
S
сhс
S bhb
S aha
2
2
2
S
)
(**)
p( p a)( p b)( p c)
2S
а
ha
2S
а
3
2S
b
hb
2S S
b
4
2
1 2S S S
p ( )
2 3 2 3
2S
с
hс
2S S
с
6
3

45.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см. Решение:
1
1
1
(*
S
сhс
S bhb
S aha
2
2
2
S
)
(**)
p( p a)( p b)( p c)
2S
b
hb
2S
а
ha
2S
а
3
2
2S S
b
4
2
3
2
1 2S S S
p ( )
2 3 2 3
2S
с
hс
2S S
с
6
3

46.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см. Решение:
1
1
1
(*
S
сhс
S bhb
S aha
2
2
2
S
)
(**)
p( p a)( p b)( p c)
2S
b
hb
2S
а
ha
2S
а
3
2
2S S
b
4
2
3
2S
с
hс
2S S
с
6
3
2
1 2S S S
1 9S 3S
p ( )
2 3 2 3
2 6
4
p a ...
p b ...
p c ...

47.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см. Решение:
1
1
1
S bhb
S aha
S сhс
(*
2
2
2
S
p( p a)( p b)( p c)
2S
а
3
2S S
b
4
2
)
(**)
2S S
с
6
3
1 2S S S
1 9S 3S
p ( )
2 3 2 3
2 6
4
3S S 5S
3S S S
3S 2S S
p a , p b , p c .
4 3 12
4 3 12
4 2 4
Все подставляем в формулу (**)

48.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см. Решение:
S
p( p a)( p b)( p c)
(**)
1 2S S S
1 9S 3S
p ( )
2 3 2 3
2 6
4
3S S S p c 3S S 5S .
3S 2S S
p a , p b ,
4 3 12
4 3 12
4 2 4
3S S S 5S
S
4 12 4 12
Преобразуйте равенство

49.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см. Решение:
S
p( p a)( p b)( p c)
(**)
1 2S S S
1 9S 3S
p ( )
2 3 2 3
2 6
4
3S S S p c 3S S 5S .
3S 2S S
p a , p b ,
4 3 12
4 3 12
4 2 4
4
3S S S 5S
15S
S
; S
;
4 12 4 12
4 4 12 12

50.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см. Решение:
S
p( p a)( p b)( p c)
(**)
1 2S S S
1 9S 3S
p ( )
2 3 2 3
2 6
4
3S S S p c 3S S 5S .
3S 2S S
p a , p b ,
4 3 12
4 3 12
4 2 4
4
3S S S 5S
15S
S
; S
;
4 12 4 12
4 4 12 12
S2
S
15 ;
48

51.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см. Решение:
S
p( p a)( p b)( p c)
(**)
1 2S S S
1 9S 3S
p ( )
2 3 2 3
2 6
4
3S S S p c 3S S 5S .
3S 2S S
p a , p b ,
4 3 12
4 3 12
4 2 4
4
3S S S 5S
15S
S
; S
;
4 12 4 12
4 4 12 12
48 S 15 ;
S2
S
15 ;
48

52.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см. Решение:
S
p( p a)( p b)( p c)
(**)
1 2S S S
1 9S 3S
p ( )
2 3 2 3
2 6
4
3S S S p c 3S S 5S .
3S 2S S
p a , p b ,
4 3 12
4 3 12
4 2 4
4
3S S S 5S
15S
S
; S
;
4 12 4 12
4 4 12 12
48 S 15 ;
48
S
15
S2
S
15 ;
48

53.

Дополнительная задача
Найдите площадь треугольника, если его
высоты равны 3см, 4см и 6см. Решение:
S
p( p a)( p b)( p c)
(**)
1 2S S S
1 9S 3S
p ( )
2 3 2 3
2 6
4
3S S S p c 3S S 5S .
3S 2S S
p a , p b ,
4 3 12
4 3 12
4 2 4
4
3S S S 5S
15S
S
; S
;
4 12 4 12
4 4 12 12
48 48 15 16 15
48 S 15 ; S
15
5
15
S2
S
15 ;
48
16 15
Ответ :
5

54.

Экспресс-опрос
Выберите верный ответ из
предложенных вариантов
1.Произведение отрезков одной из двух пере
секающихся хорд равно
a) квадрату суммы отрезков другой хорды;
b) произведению отрезков другой хорды
c) длине другой хорды.

55.

Если две хорды окружности
пересекаются, то произведение
отрезков одной хорды равно
произведению отрезков другой хорды
К
АЕ ЕК СЕ ЕD

56.

Выберите верный ответ
2. Квадрат касательной равен
a) Произведению секущей
на ее внешнюю часть;
b) Произведению отрезка секущей,
заключенного внутри окружности,
на ее внешнюю часть;
c) Произведению секущей на отрезок
секущей, заключенный внутри
окружности.

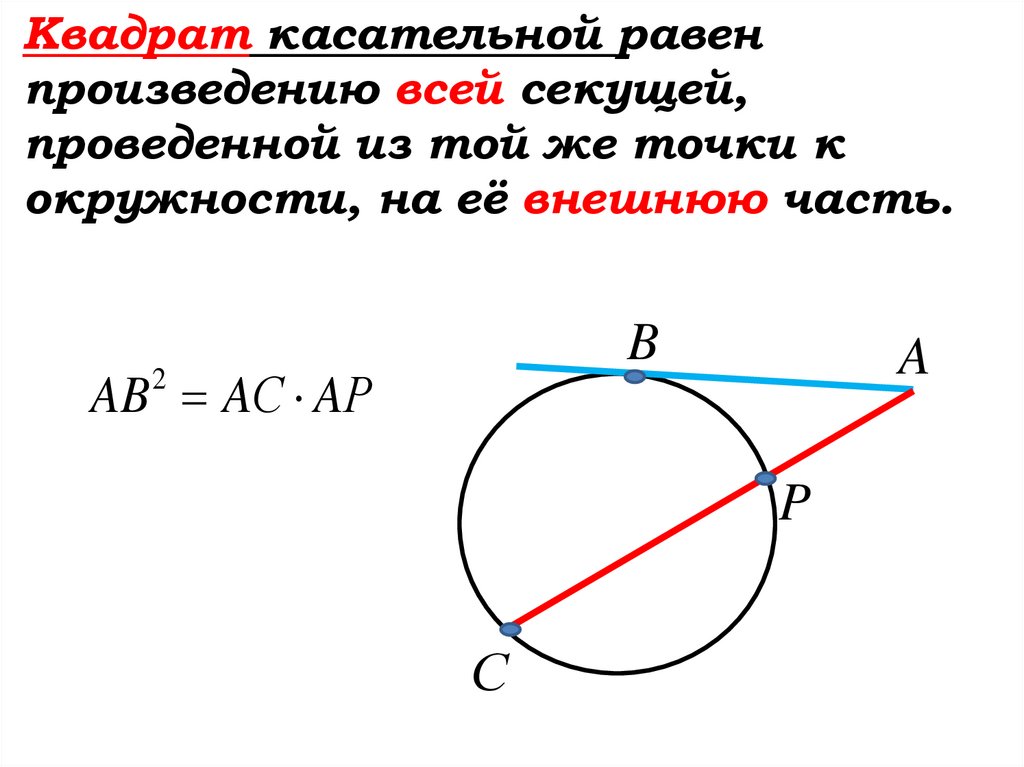
57.

Квадрат касательной равен
произведению всей секущей,
проведенной из той же точки к
окружности, на её внешнюю часть.
B
AB AС AР
2
A
P
С

58.

Выберите верный ответ
3.Угол между двумя пересекающимися
хордами измеряется
a) Полуразностью заключенных между ним
и дуг
b) Половиной произведения заключенных
между ними дуг
c) Полусуммой заключенных между ними дуг

59.

Если угол образован двумя
пересекающимися хордами, то он
равен половине суммы дуг,
заключенных между этими хордами
А
1
1 ( AC BD )
2
С
1
В
D

60.

Выберите верный ответ
4. Угол между двумя секущими,
проведенными из одной точки,
измеряется
a) Полуразностью заключенных
между ними дуг;
b) Половиной произведения
заключенных между ними дуг;
c) Полусуммой заключенных между
ними дуг.

61.

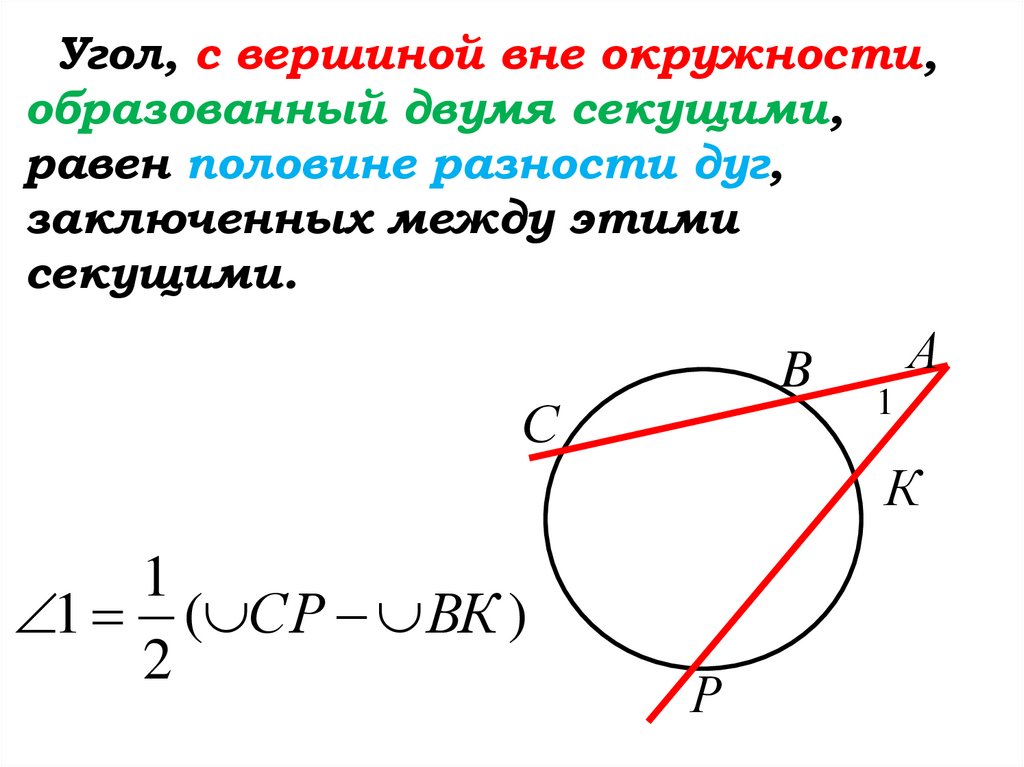
Угол, с вершиной вне окружности,
образованный двумя секущими,
равен половине разности дуг,
заключенных между этими
секущими.
B
С
А
1
К
1
1 ( СР ВК )
2
Р

62.

Выберите верный ответ
5. Угол между касательной и
хордой, проходящей через точку каса
ния, измеряется
a) Дугой, на которую он опирается;
b) Половиной заключенной в нем дуги;
c) Полуразностью заключенных
между ними дуг.

63.

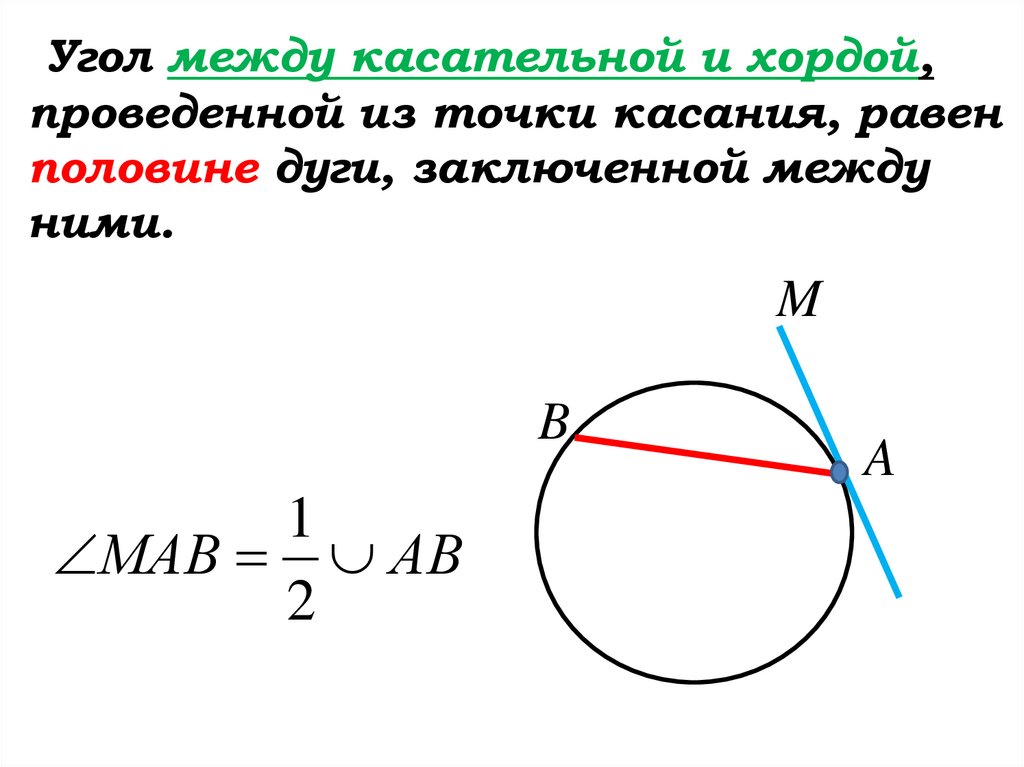
Угол между касательной и хордой,
проведенной из точки касания, равен
половине дуги, заключенной между
ними.
M
B
1
МАВ АВ
2
A

64.

Выберите верный ответ
6.Угол между касательной и секущей,
проведенными из одной точки
a) Равен 180 минус величина заключенной
внутри него дуги большей полуокружности;
b) измеряется полуразностью
заключенных внутри него дуг;
c) Равен 180 минус величина заключенной
внутри него дуги меньшей полуокружности.

65.

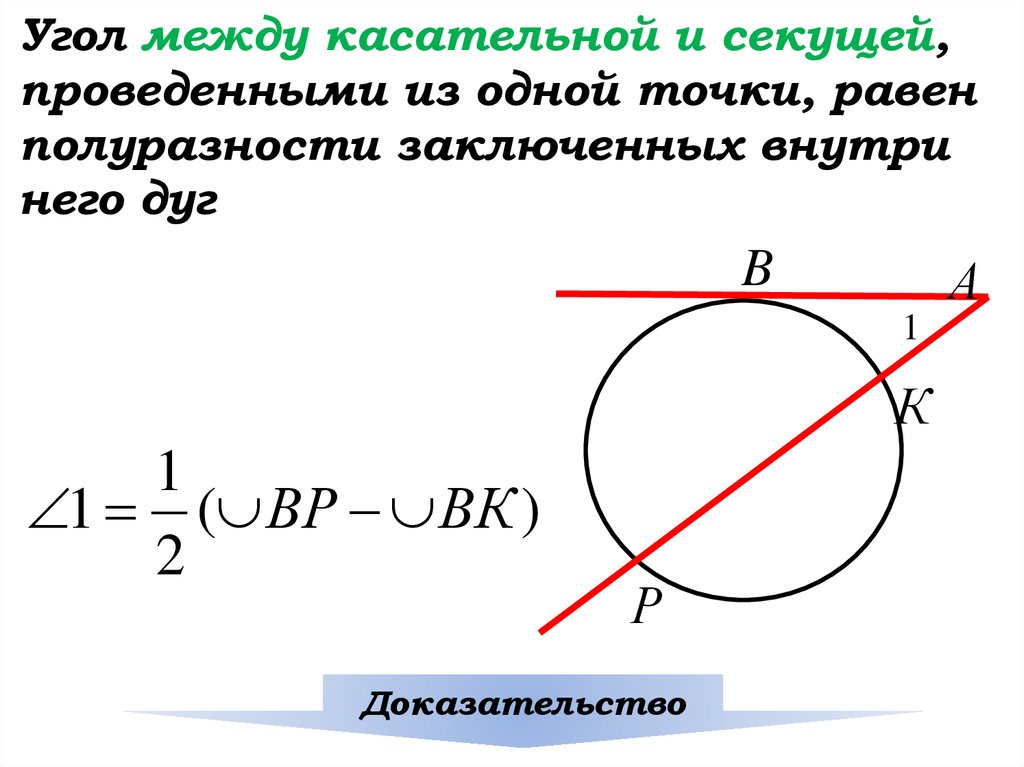
Угол между касательной и секущей,
проведенными из одной точки, равен
полуразности заключенных внутри
него дуг
B
А
1
К
1
1 ( ВР ВК )
2
Р
Доказательство

66.

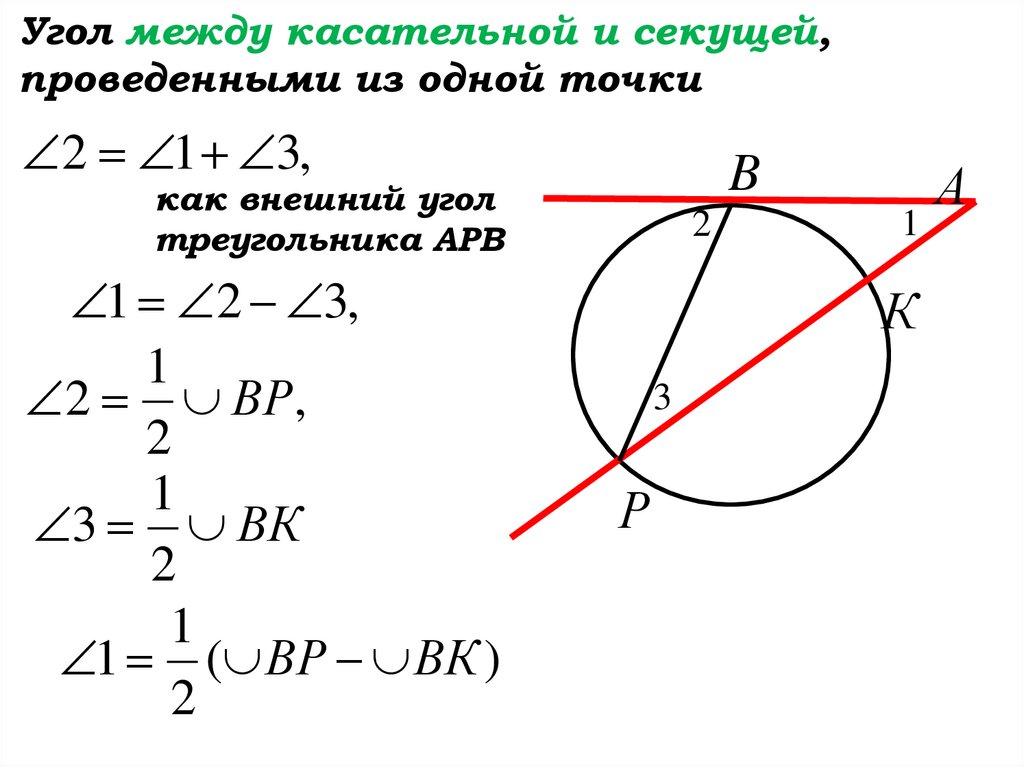
Угол между касательной и секущей,
проведенными из одной точки
2 1 3,
B
как внешний угол
треугольника АРВ
1 2 3,
1
2 ВР,
2
1
3 ВК
2
1
1 ( ВР ВК )
2
2
1
К
3
Р
А

67.

Выберите верный ответ
7.
В любом вписанном четырехугольнике
a)Суммы противоположных сторон
равны;
b)Суммы односторонних углов
равны 180 ;
c)Суммы противоположных углов
равны 180 .

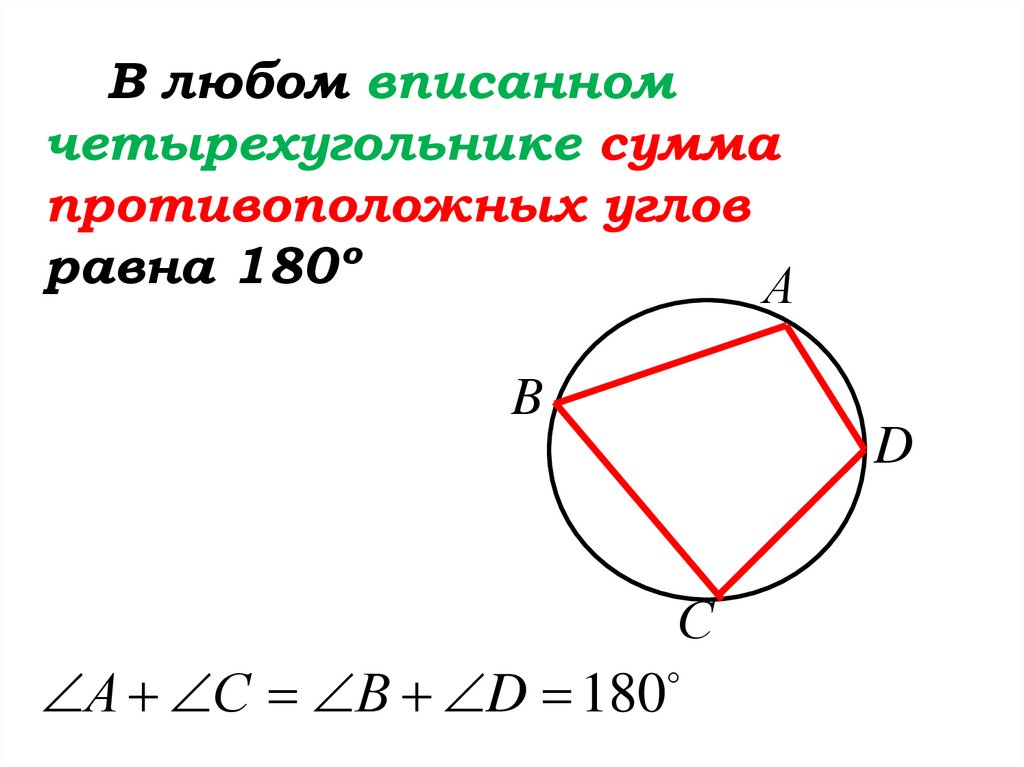
68.

В любом вписанном
четырехугольнике сумма
противоположных углов
равна 180º
А
B
D
С
А С В D 180

69.

Выберите верный ответ
8. В выпуклый четырехугольник
можно вписать окружность, если
a)Суммы противоположных сторон
равны;
b)Суммы односторонних углов равны
180 ;
c)Суммы противоположных углов
равны 180 .

70.

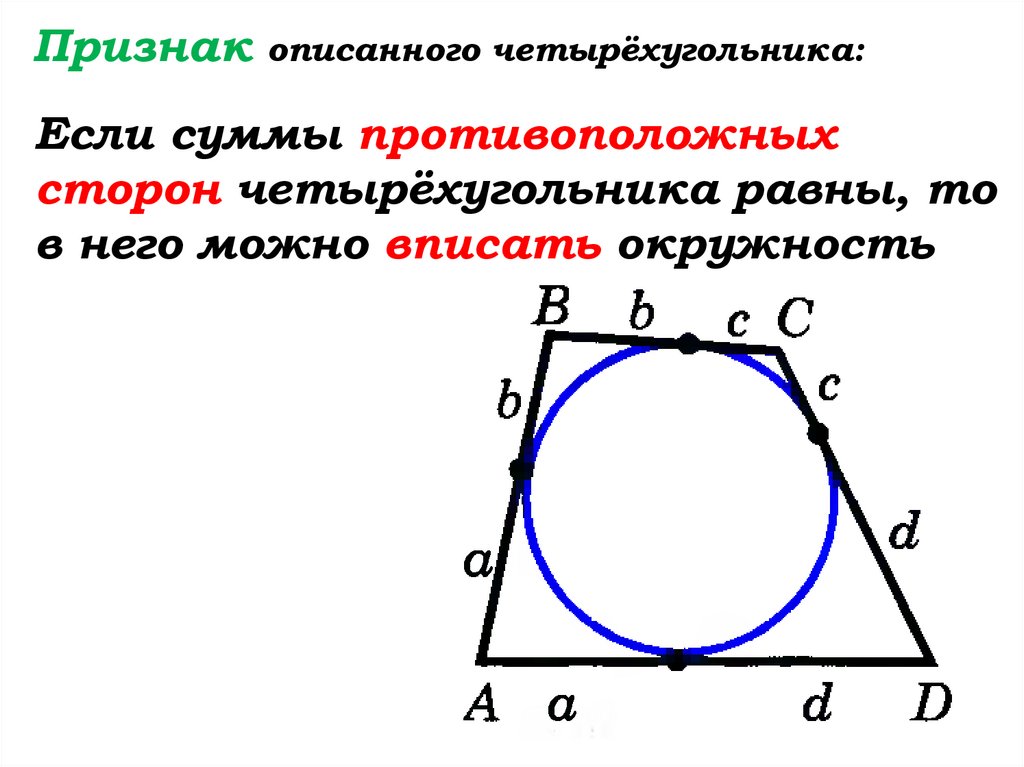
Признак описанного четырёхугольника:
Если суммы противоположных
сторон четырёхугольника равны, то
в него можно вписать окружность

71.

Выберите верный ответ
9.Угол между двумя касательными,
проведенными из одной точки,
a)Равен 180 минус величина заключ
енной внутри него дуги большей
полуокружности;
b)измеряется полуразностью
заключенных внутри него дуг;
c)Равен 180 минус величина заключ
енной внутри него дуги меньшей
полуокружности

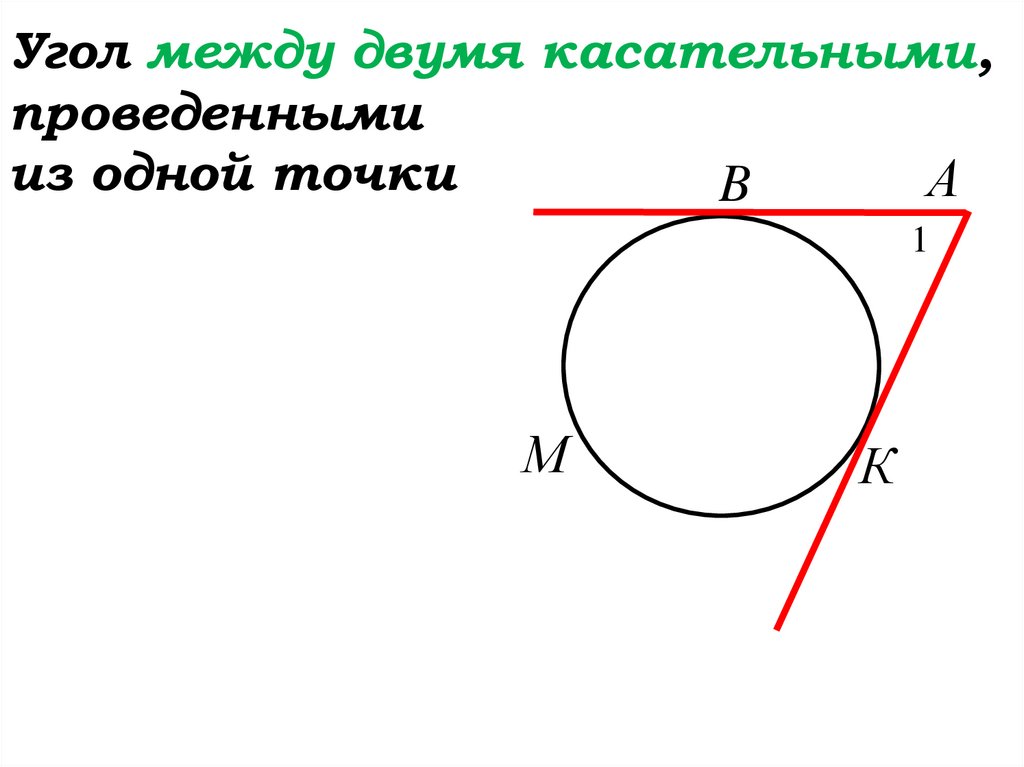
72.

Угол между двумя касательными,
проведенными
из одной точки
А
B
1
М
К

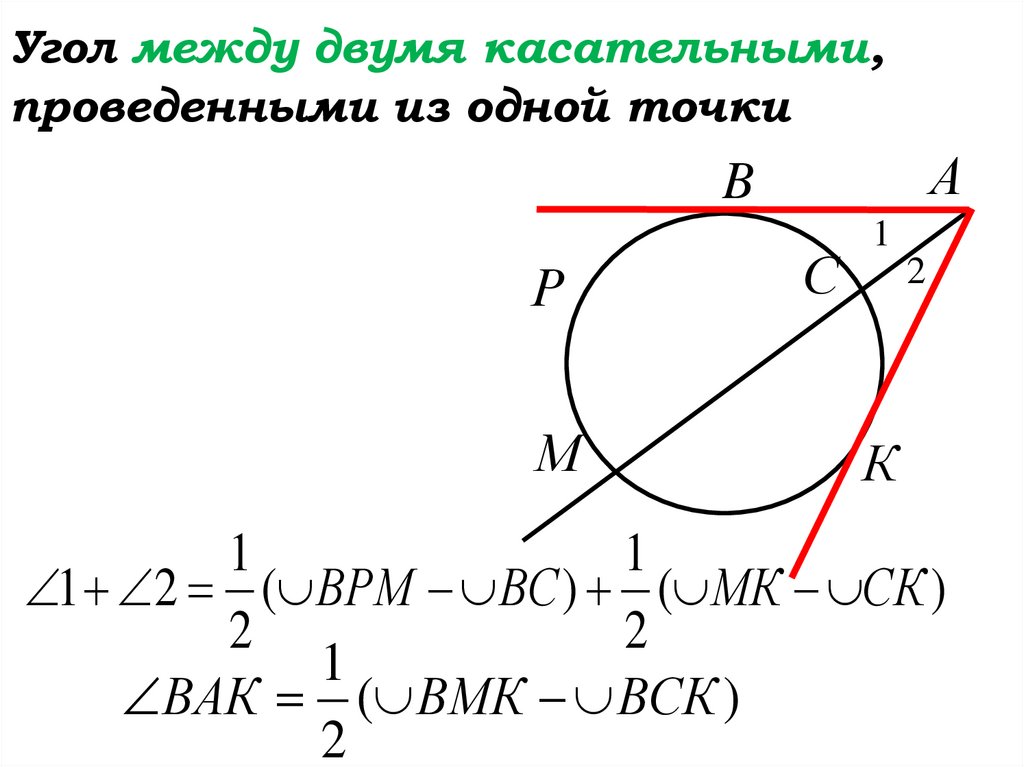
73.

Угол между двумя касательными,
проведенными из одной точки
А
B
Р
М
С
1
2
К
1
1
1 2 ( ВРМ ВС ) ( МК СК )
2
2
1
ВАК ( ВМК ВСК )
2

74.

Выберите верный ответ
9.Угол между двумя касательными,
проведенными из одной точки,
a) Равен 180 минус величина
заключенной внутри него дуги
большей полуокружности;
b) измеряется полуразностью
заключенных внутри него дуг;
c) Равен 180 минус величина заключе
нной внутри него дуги, меньшей
полуокружности

75.

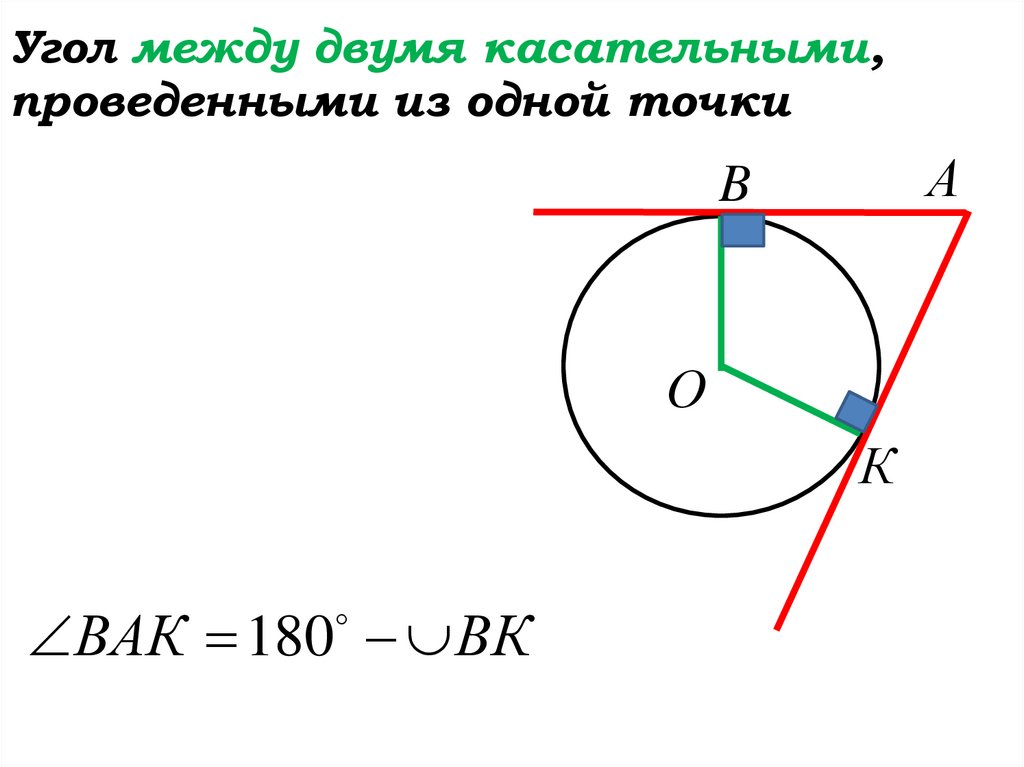
Угол между двумя касательными,
проведенными из одной точки
А
B
О
К
ВАК 180 ВК

76.

Выберите верный ответ
10. Из теоремы о квадрате медианы
треугольника можно вывести формулу
медианы треугольника:
.
1
ma= 2
2b 2 2c 2 a 2
1
mc= 2
2b 2 2c 2 a 2
1
mb= 2
2b 2 2c 2 a 2

77.

Выберите верный ответ
10. Из теоремы о квадрате медианы
треугольника можно вывести формулу
медианы треугольника:
.
1
ma= 2
2b 2 2c 2 a 2
1
mc= 2
2b 2 2c 2 a 2
1
mb= 2
2b 2 2c 2 a 2

78.

Выберите верный ответ
11.Сумма квадратов диагоналей
параллелограмма равна
a)Сумме квадратов его сторон;
b)Полусумме квадратов его сторон;
c)Половине произведения его смежных
.
сторон.

79.

Сумма квадратов диагоналей
параллелограмма равна
сумме квадратов его сторон
.

80.

Выберите верный ответ
13. Биссектриса треугольника делит
его сторону на части
a) Пропорциональные двум другим
сторонам;
b) Пропорциональные двум другим
биссектрисам;
c) Пропорциональные квадратам
.
двух других сторон.

81.

Биссектриса треугольника делит его
сторону на части пропорциональные
двум другим сторонам
В
А
D
С
ВD DС
АB AС

82.

Выберите верный ответ
14.Теорема косинусов
выражается формулой
a)с 2 a 2 b 2 2ab cos
a
b
c
b)
2R
sin А sin В sin С
a2 b2 c2
c)сos С=
2ab

83.

Выберите верный ответ
14.Теорема косинусов
выражается формулой
a)с 2 a 2 b 2 2ab cos
a
b
c
b)
2R
sin А sin В sin С
a2 b2 c2
c)сos С=
2ab

84.

Формулы для нахождения площади треугольника:
1
аh
1) Произвольного (через сторону и высоту): S
2
1
2) Прямоугольного: S 2 аb 2
a 3
3) Равностороннего:
S
4) Формула Герона: S
р( р а)( р b)( p c)
4
2а 2 sin B sin C
5) Через синусы углов треугольника: S
sin A
S 2 R 2 sin A sin B sin C
1
аb sin C
.
2
1
S
Рr pr
7) Через радиус вписанной окружности:
2
abc
8) Через радиус описанной окружности: S 4 R
6)Через 2 стороны и угол между ними: S

85.

Подводим итоги урока:
1 уровень: Вы понимали все, что
предлагалось на уроке. Все формулы
площадей понятны, рассмотренные
вопросы усвоены- отличный результат.
2 уровень: сегодня многие вопросы
остались непонятыми. Вспоминать было
трудно. С вычислениями есть проблемы.
Много пробелов в раннее пройденном
материале. Следует позаниматься.
Рекомендации: Материал каждого урока
разбирать по конспекту урока на сайте.

86.

Оцените урок и результат своей деятельности
Выберите один из вариантов.
На уроке я работал
Своей работой на уроке я
Урок для меня показал
За урок я
активно / пассивно
доволен / не доволен
коротким / длинным
устал / не устал
Материал урока мне был
понятен / не понятен
интересен / скучен
За урок я ставлю себе
оценку
_________________

87.

ДР№5 на 12.10.17
1.Теория. Выучить формулы площади
треугольника. Проработать материал по
формулам эллипса, гиперболы и параболы
окружности. Учебник «Геометрия 10-11»
2.Практика. Постройте линии второго
порядка:
х2 y2
х2 y2
a)
25
9
1
б)
16
4
1
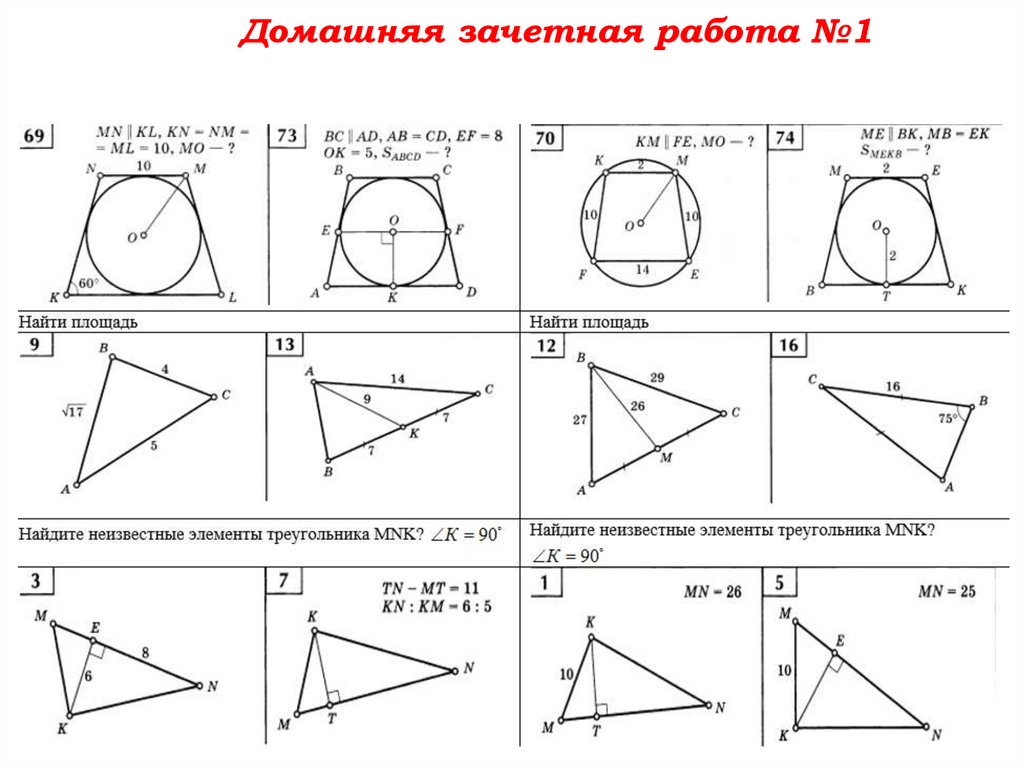
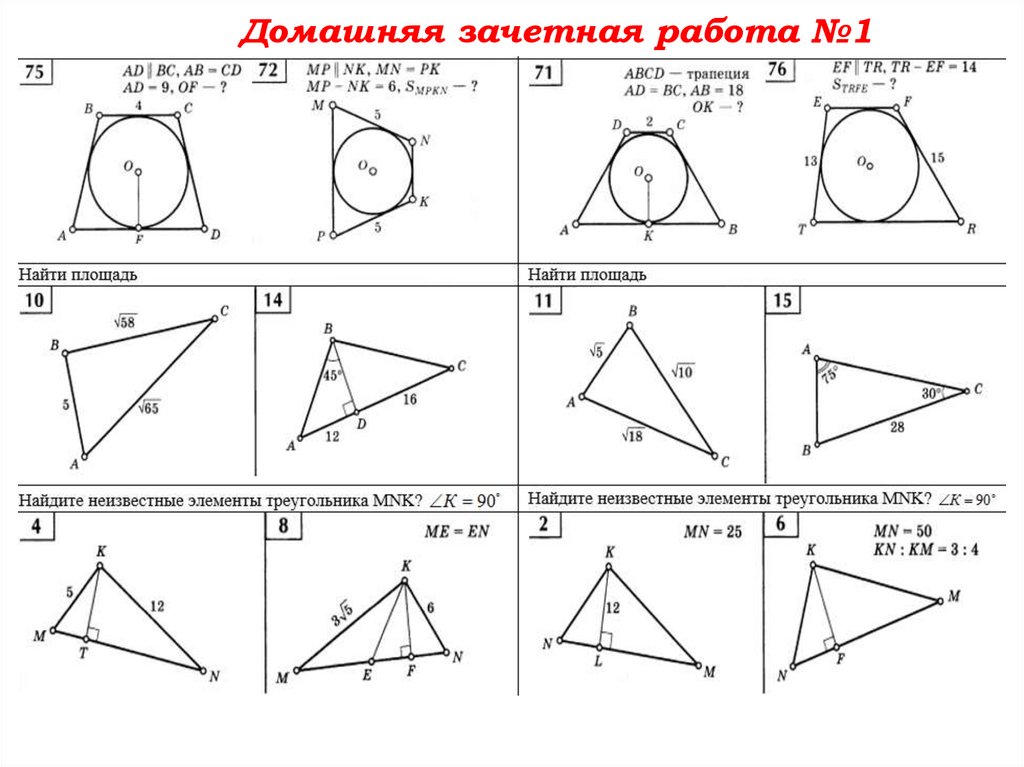
3. Выполните домашнюю зачетную
работу.

88.

Домашняя зачетная работа №1

89.

Домашняя зачетная работа №1