Похожие презентации:
Дискретные случайные величины. Лекция 8
1.
Лекция 8Дискретные случайные величины
2.
Понятие случайной величиныСлучайной называют величину, которая в результате испытания
примет одно и только одно числовое значение, зависящее от случайных
факторов и заранее непредсказуемое.
Случайные величины, как правило, обозначают через X, Y, Z, а их
значения соответствующими маленькими буквами: x1, x2, x3.
Пример1: Пусть X - количество очков, которое выпадет после броска
игрального кубика.
В результате данного испытания выпадет одна и только грань, какая
именно – не предсказать; при этом случайная величина X может принять
одно из следующий значений: x1=1, x2=2, x3=3, x4=4, x5=5, x6=6.
Пример 2: Пусть Y - количество мальчиков среди 10 новорождённых.
В этом десятке может оказаться: y0=0, y1=1, y2=2, y3=3, y4=4, y5=5, y6=6,
y7=7, y8=8, y9=9, y10=10 мальчиков. Один и только один из перечисленных
вариантов.
3.
Пример 3: Пусть Z – дальность прыжка в длину.Ее сложно предугадать заранее. Случайная величина Z может принять несчётно
много значений из некоторого числового промежутка. И в этом состоит её
принципиальное отличие от предыдущих примеров.
Таким образом, случайные величины целесообразно разделить на 2
большие группы:
1) Дискретная (прерывная) случайная величина (ДСВ) – принимает отдельно
взятые, изолированные значения. Количество этих
значений конечно либо бесконечно, но счётно.
2) Непрерывная случайная величина (НСВ) – принимает все числовые
значения из некоторого конечного или бесконечного промежутка.
4.
Дискретные случайные величиныПусть Ω = {ω} − пространство элементарных событий некоторого
опыта, а X = {x} − конечное (или сравнимое с множеством
натуральных чисел) числовое множество.
Определение 1. Функция, отображающая пространство Ω в
множество X, называется дискретной случайной величиной.
Определенная таким образом дискретная случайная величина
обозначается X = X(ω).
Для задания случайной величины недостаточно задать только
множество ее значений. Необходимо также определить вероятности
событий, связанных с этими значениями.
5.
Закон распределения дискретной случайнойвеличины
6.
Определение2. Отображение, при котором каждому возможномузначению дискретной случайной величины соответствует вероятность
события, при котором случайная величина принимает это значение,
называется законом распределения дискретной случайной величины.
Так как закон распределения является числовой функцией, то его можно
задать в виде таблицы, или графика, или аналитически с помощью
некоторой формулы.
Табличное задание закона распределения
При табличном задании значения случайной величины упорядочивают
по возрастанию, записывая в первой строке таблицы, а
соответствующие значения вероятностей располагают во второй ее
строке:
p
x1
p1
x2 ... xn 1
p2 ... pn 1
xn
pn
Критерием правильности составления закона распределения является
условие
7.
Пример. Дан закон распределения дискретной случайной величины.Найдите неизвестную вероятность.
2
p 0,46
5
p2
8
11
0,11 0,14
8.
Пример. Дан закон распределения дискретной случайной величины.Найдите неизвестную вероятность.
2
p 0,46
5
p2
8
11
0,11 0,14
Решение. Так как таблица представляет закон распределения
дискретной случайной величины, то сумма вероятностей во второй
строке должна быть равна единице. Пусть неизвестная вероятность
равна p2. Тогда, 0,46 + p2 + 0,11 + 0,14 = 1.
Следовательно, p = 1 − 0, 46 − 0,11 − 0,14 ⇒ p = 0, 29.
9.
Пример 2.10.
Пример 2.11.
Пример 3.12.
Пример 3.13.
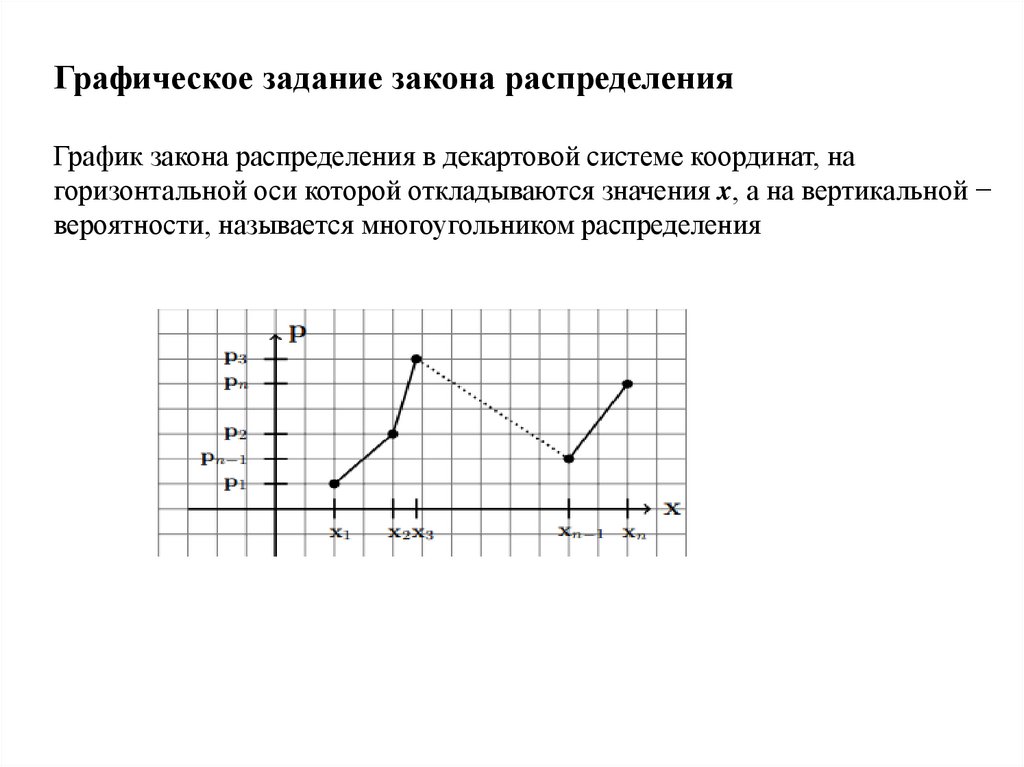
Графическое задание закона распределенияГрафик закона распределения в декартовой системе координат, на
горизонтальной оси которой откладываются значения x, а на вертикальной −
вероятности, называется многоугольником распределения
14.
Пример. Постройте многоугольник распределения для заданного распределения2
5
8
11
p 0,46 0,29 0,11 0,14
Решение. В системе координат x − p построим точки, взяв за их координаты
соответствующие значения из закона распределения дискретной случайной
величины. Построенные точки соединим пунктирной линией:
15.
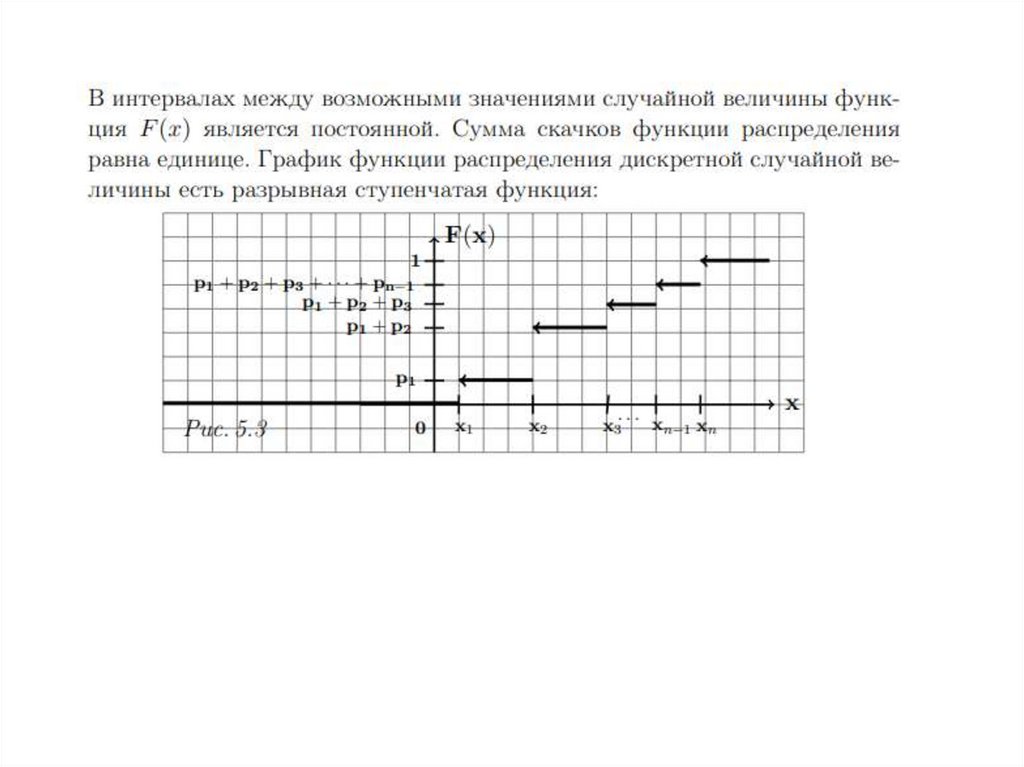
Функция распределения дискретной случайной величины.Еще одной геометрической иллюстрацией дискретной случайной величины
является ее функция распределения.
Определение. Функцией распределения случайной величины называется
функция, которая в каждой точке x числовой прямой определяет
вероятность события, в котором случайная величина принимает значение,
меньшее, чем x.
То есть, F ( x) P( X x) .
Таким образом, вероятность того, что X < x зависит от x, поэтому
функция F(x) называется функцией распределения.
С точки зрения геометрии функция распределения определяет
вероятность того, что случайная величина X в результате исхода попадет
на координатную прямую левее x:
16.
px1
p1
x2 ... xn 1
p2 ... pn 1
xn
pn
17.
18.
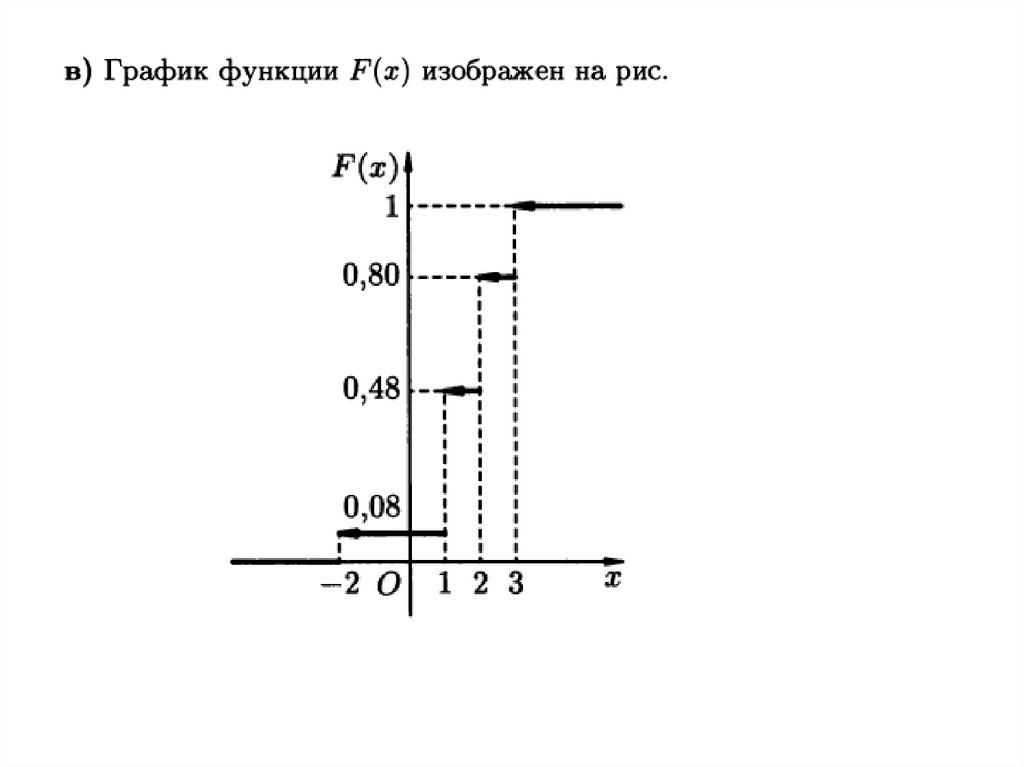
Пример.19.
20.
21.
Пример.22.
23.
24.
25.
26.
27.
28.
Математическое ожидание распределения дискретнойслучайной величины
Если представлять множество значений случайной величины как
некоторый интервал, расположенный на числовой прямой, то нужно
знать «центр» этого интервала, то есть места, где расположена
основная «масса вероятности». А также нужно знать «радиус» этого
интервала, как «меру рассеяния» этой «массы вероятности»
относительно «центра».
Пусть известен закон распределения дискретной случайной величины
X:
p
x1
p1
x2 ... xn 1
p2 ... pn 1
xn
pn
29.
Определение: Математическим ожиданием случайной величины Xназывается скалярное произведение вектора значений случайной
величины на вектор соответствующих им вероятностей. То есть,
M ( X ) x1 p1 x2 p2 ... xn 1 pn 1 xn pn
или
n
M ( X ) xi pi
i 1
Пример: Найти математическое ожидание для заданного закона
распределения:
2
5
8
11
p 0,46 0,29 0,11 0,14
Решение: M(X) = 2 · 0, 46 + 5 · 0, 29 + 8 · 0, 11 + 11 · 0, 14 = 4,79
30.
Пример. В магазине продаются 5 отечественных и 3 импортныххолодильника. Случайная величина Х − число импортных холодильников
из четырех наудачу выбранных холодильников.
1. Составьте закон распределения случайной величины Х.
2. Вычислите математическое ожидание случайной величины Х.
31.
Решение. Найдем общее число вариантов выбора 4-х холодильников изимеющихся 8. Так как мы не делаем между холодильниками различий, то
выбор реализуется с помощью сочетаний: Далее, рассмотрим
благоприятные варианты выбора и вычислим соответствующие
8!
вероятности событий.
n C4
70
8
4!4!
1.Х=0: выбрали 0 импортных холодильников из 3 импортных и
выбрали 4 отечественных холодильника из 5 отечественных.
m Х 0
C30 C54 1 5 5 , тогда
p0
m Х 0 5
n
70
2. Х =1: выбрали 1 импортный холодильник из 3 импортных и
выбрали 3 отечественных холодильника из 5 отечественных.
m Х 1 C31 C53 3 10 30
p1
m Х 1 30
n
70
3. Х =2: выбрали 2 импортных холодильник из 3 импортных и
выбрали 2 отечественных холодильника из 5 отечественных.
m Х 2 C32 C52 3 10 30
p2
m Х 1 30
n
70
32.
4.Х=3: выбрали 3 импортных холодильник из 3 импортных и выбрали1 отечественный холодильник из 5 отечественных.
m Х 3 C33 C51 1 5 5
p3
m Х 1 5
n
70
Закон распределения дискретной случайной величины P имеет следующий
вид:
.
Х 0
1
2
3
5 30 30 5
p
70 70 70 70
Проверим правильность вычислений:
5 30 30 5
1
70 70 70 70
Вычислим математическое ожидание дискретной случайной величины Х:
M (X ) 0
5
30
30
5 105
1
2
3
1,5
70
70
70
70 70
33.
Пример. Из опыта сдачи экзамена некоторому преподавателю предыдущимипоколениями студентов установлено, что сдать ему экзамен на «отлично»
можно с вероятностью 0, 3, на «хорошо» − с вероятностью 0, 4. Какова
вероятность получить у этого преподавателя другие оценки, если
математическое ожидание случайной величины S, связанной с
распределением оценок у данного преподавателя при случайно выбранном
билете, равно 3, 9.
Решение. Согласно Положению о высшей школе, S может принимать значения
из множества {2 3, 4, 5}. Допустим, что x и y − вероятности того, что
сдающий может соответственно получить оценки «неудовлетворительно» и
«удовлетворительно». Составим предполагаемый закон распределения
дискретной случайной величины S:
S 2 3 4
5
p
x
y 0,4 0,3
Cумма вероятностей должна быть равна единице, поэтому x+y+0,4+0,3 = 1.
Кроме этого, согласно условию формуле для нахождения мат. ожидания,
имеем 2x + 3y + 4 · 0, 4 + 5 · 0, 3 = 3, 9.
Решив систему, получим x = 0, 1, а y = 0, 2. Следовательно, у данного
преподавателя можно получить «удовлетворительно» с вероятностью 0,2 и
«неудовлетворительно» с вероятностью 0,1.
34.
Замечание. В том случае, когда дискретная случайная величина Xпринимает бесконечное множество значений, ее математическое
ожидание является суммой абсолютно сходящегося ряда:
n
M ( X ) xi pi
i 1
С точки зрения теории вероятности математическое ожидание
приблизительно равно среднему арифметическому возможных
значений дискретной случайной величины.
35.
Свойства математического ожиданияСвойство 1. Математическое ожидание постоянной величины равно
самой постоянной величине: M(C) = C.
Свойство 2. Постоянный множитель можно выносить за знак
математического ожидания: M(CX) = CM(X).
Свойство 3. Математическое ожидание суммы двух случайных величин
равно сумме их математических ожиданий: M(X + Y ) = M(X) + M(Y ).
Чтобы сформулировать следующее свойство, понадобится следующее
Определение. Две случайные величины называются независимыми, если
закон распределения одной из них не зависит от того, какие возможные
значения может принимать другая величина.
Свойство 4. Математическое ожидание произведения двух независимых
случайных величин равно произведению их математических ожиданий:
M(XY ) = M(X) · M(Y ).
36.
Дисперсия дискретной случайной величиныМатематическое ожидание как характеристика случайной величины дает
много информации о ней, но, как видно из следующих примеров, этой
информации оказывается недостаточно.
Рассмотрим законы распределения двух случайных величин:
Х
p
0,1 0,1
0,5 0,5
Х
p
100 100
0,5 0,5
Найдем математические ожидания каждой из случайных величин:
M(X) = −0, 1 · 0, 5 + 0, 1 · 0, 5 ⇒ M(X) = 0.
M(Y ) = −100 · 0, 5 + 100 · 0, 5 ⇒ M(Y ) = 0.
Случайные величины X и Y имеют одинаковые математические
ожидания, но их возможные значения не равны. При этом, в одном случае
возможные значения располагаются вблизи математического ожидания, а в
другом случае удалены от него.
Проблема заключается в отсутствии информации о рассеянии
возможных значений случайных величин относительно математического
ожидания. Чтобы исследовать вопрос о рассеянии, рассмотрим отклонение
случайной величины от ее математического ожидания.
37.
Определение. Отклонением называется разность между случайнойвеличиной X и ее математическим ожиданием M(X).
Из определения следует, что отклонение X −M(X) является случайной
величиной, обладающей следующим свойством.
Теорема 1. Математическое ожидание отклонения случайной величины от
ее математического ожидания равно нулю: M(X − M(X)) = 0.
Используя свойства 1 и 4 математического ожидания, имеем
M(X − M(X)) = M(X) − M(M(X)) = M(X) − M(X) = 0.
Из данной теоремы вытекает, что определять рассеяние возможных
значений случайной величины с помощью математического ожидания
отклонения невозможно. Объяснить это можно тем, что одни отклонения
являются положительными числами, а другие − отрицательными. Поэтому
их алгебраическая сумма обращается в нуль. Вследствие этого возникают
два варианта: исследовать математическое ожидание модуля отклонения или
квадрата отклонения. Практическое применение получил второй вариант.
38.
Определение. Дисперсией дискретной случайной величины называетсяматематическое ожидание квадрата отклонения случайной величины от ее
математического ожидания:
D( X ) M ( X M ( X )) 2
Замечание. Из определения следует, что дисперсия случайной величины
является неотрицательной константой. При расчетах дисперсии ее
определение оказывается очень неудобным в силу большого числа
вычислений. Поэтому рассмотрим следующую теорему.
Теорема 2. Формула вычисления дисперсии Дисперсия равна разности
между математическим ожиданием квадрата случайной величины и
квадратом ее математического ожидания:
39.
Теорема 2. Формула вычисления дисперсии Дисперсия равна разностимежду математическим ожиданием квадрата случайной величины и
квадратом ее математического ожидания:
D( X ) M ( X 2 ) ( M ( X )) 2
Используя свойства математического ожидания, получим:
M ( X M ( X )) 2 M X 2 2 Х M ( X ) ( M ( X )) 2
M ( X 2 ) 2M ( X ) M ( X ) ( M ( X )) 2
M ( X 2 ) 2( M ( X )) 2 ( M ( X )) 2
M ( X 2 ) ( M ( X )) 2
40.
Свойства дисперсииСвойство 1. Дисперсия постоянной величины C равна нулю: D(C) = 0.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии,
предаварительно возведя его в квадрат: D(СХ ) С 2 D( Х )
Свойство 3. Дисперсия суммы двух независимых случайных величин равна
сумме дисперсий этих величин: D(X + Y ) = D(X) + D(Y ).
Свойство 4. Дисперсия разности двух независимых случайных величин равна
сумме дисперсий этих величин: D(X − Y ) = D(X) + D(Y ).
Замечание. Заметим, что свойство 3 имеет место для любого конечного числа
взаимно независимых случайных величин:
D(X1 + X2 + · · · + Xn ) = D(X1 ) + D(X2 ) + · · · + D(Xn ).
41.
Пример: Найти дисперсию для заданного закона распределения2
5
8
11
p 0,46 0,29 0,11 0,14
Решение. Для того, чтобы вычислить дисперсию дискретной случайной
величины, дополним таблицу ее закона распределения строчкой
квадратов ее значений:
Х2
Х
p
4
25
64 121
2
5
8
11
0,46 0,29 0,11 0,14
Вычислим M ( X 2 )= 4 · 0, 46 + 25 · 0, 29 + 64 · 0, 11 + 121 · 0, 14
⇒ M ( X 2 ) = 23, 07.
Найдем и возведем в квадрат значение математического ожидания:
M ( X ) 2 2 0,46 5 0,29 8 0,11 11 0,14 2 4,79 2 22,94
M ( X 2 ) ( M ( X )) 2 23,07 22,94 0,13
D(Х)=0,13
42.
Пример. Закон распределения дискретной случайной величины Х имеетследующий вид:
.
Х 0
1
2
3
5 30 30 5
p
70 70 70 70
Решение. Аналогично решению предыдущей задачи дополним таблицу
значений закона распределения случайной величины Х строкой из
квадратов ее значений:
2
Х
Х
p
0
0
5
70
1
1
30
70
4
2
30
70
9
3
5
70
Вычислим M ( X 2 ) = 0·(1\14) + 1·(3 \7) + 4·(3\ 7) + 9·(1 \14)
11
2
2
. M(Х) = 1,5, найдем его квадрат: M ( X ) 1,5. 2,25
14
11
1 15
2
2
M
(
X
)
(
M
(
X
))
2
2
Получаем: D(P)=
≈ 0, 54.
14
4 28
⇒ M (X 2) 2
43.
Пример:Пример:
44.
Пример. Известно, что некоторая случайная величина может приниматьзначения 0, 3 и 5. Известно, что математическое ожидание равно 2, а
дисперсия 3. Найдите закон распределения случайной величины.
Решение. Предположим, что события, соответствующие указанным
значениям, наступают соответственно с вероятностями p1, p2 и p3. Тогда
таблица закона распределения данной случайной величины вместе с
дополнительной строкой квадратов ее значений будет иметь следующий
вид:
Х 2 0 9 25
Х
0 3
5
pi p1 p2 p3
Для вероятностей имеет место равенство: p1 p2 p3 1 .
Из условия задачи и формулы для математического ожидания данной
случайной величины можно составить следующее равенство:
0 p1 3 p2 5 p3 2
Зная дисперсию случайной величины с помощью формулы можно
получить еще одно равенство:
0 p1 9 p2 25 p3 2 2 3
45.
Cоставим следующую систему уравнений:p1 p2 p3 1
0 p1 3 p2 5 p3 2
0 p 9 p 25 p 2 2 3
1
2
3
Решив систему, находим p1 = 0, 4; p2 = 0, 5; p3 = 0, 1.
Следовательно, закон распределения данной случайной величины имеет
такой вид:
Х
pi
0
3
5
0,4 0,5 0,1
46.
Пример:47.
48.
Среднее квадратическое отклонениеТак как дисперсия определяет квадрат отклонения случайной величины от
ее среднего значения, то кроме нее вводят еще одну характеристику.
Определение: Средним квадратическим отклонением случайной величины
X называется квадратный корень из ее дисперсии: ( Х ) D( Х ) .
Теорема. Среднее квадратическое отклонение суммы двух независимых
случайных величин равно квадратному корню из суммы квадратов
среднеквадратических отклонений этих величин:
( Х Y ) 2 ( Х ) 2 (Y )
49.
Пример:50.
51.
Пример: Две случайные величины X и Y заданы своими законамираспределения:
Х
pi
1.
2.
1
2
3
0,5 0,3 0,2
Х
p
1 0
1
2
0,2 0,3 0,4 0,1
Вычислите M(X − 2Y ) и D(X − 2Y ).
Вычислите M(2X + 3Y ) и D(2X + 3Y ).
Решение. Вычислим для каждой из случайных величин
математическое ожидание и дисперсию.
M(X) = 1 · 0, 5 + 2 · 0, 3 + 3 · 0, 2 ⇒ M(X) = 1, 7;
M(Y ) = −1 · 0, 2 + 0 · 0, 3 + 1 · 0, 4 + 2 · 0, 1 ⇒ M(Y ) = 0, 4.
Для того, чтобы вычислить дисперсии, надстроим в каждой из таблиц
строки квадратов значений величин:
Х2
Х
p
1
4
9
1
2
3
0,5 0,3 0,2
Х2
Х
p
1
0
1
2
1 0
1
2
0,2 0,3 0,4 0,1
52.
Вычислим: M ( X 2 ) и M (Y 2 )M ( X 2 ) = 1 · 0, 5 + 4 · 0, 3 + 9 · 0, 2 ⇒ M ( X 2 ) = 3, 5;
M (Y 2 ) = 1 · 0, 2 + 0 · 0, 3 + 1 · 0, 4 + 4 · 0, 1 ⇒ M (Y 2 ) = 1.
Найдем дисперсии заданных случайных величин:
2
2
D( Х ) 3,5 1,7 0,61; D(Y ) 1 0,4 0,84
Используя свойства математического ожидания случайных величин,
определим математические ожидания заданных линейных
комбинаций случайных величин:
M(X − 2Y ) = M(X) − 2M(Y ) ⇒ M(X − 2Y ) = 1, 7 − 2 · 0, 4 = 0, 9;
M(2X + 3Y ) = 2M(X) + 3M(Y ) ⇒ M(2X + 3Y ) = 2 · 1, 7 + 3 · 0, 4 ⇒
M(2X + 3Y ) = 4, 6.
Так как X и Y − независимые случайные величины, то с помощью
свойств 2 и 3 вычислим дисперсии указанных линейных комбинаций
случайных величин: D(X − 2Y ) = D(X) − 4D(Y ) ⇒D(X − 2Y ) = 0, 61+
+ 4 · 0, 84 ⇒ D(X − 2Y ) = 3, 97;
D(2X + 3Y ) = 4D(X) + 9D(Y ) ⇒ D(2X + 3Y ) = 4 · 0, 61 + 9 · 0, 84 ⇒
D(2X + 3Y ) = 10.
В итоге, имеем M(X − 2Y ) = 0, 9; D(X − 2Y ) = 3, 97;
M(2X + 3Y ) = 4, 6; D(2X + 3Y ) = 10.
53.
Пример: Подбрасывают два игральных кубика. Случайная величина X− сумма выпавших очков. Найдите закон распределения,
математическое ожидание и дисперсию.
Решение. Каждый кубик имеет 6 одинаковых граней. Так как каждый кубик
подбрасывается независимо от другого, то согласно принципу произведения,
общее число вариантов выпадения двух цифр на кубиках равно n = 6 · 6, то
есть, n = 36.
При этом сумма выпавших очков может принимать все целочисленные
значения от двух (если выпадет вариант 1-1), до 12 (если выпадет вариант 66).
1. X=2, A2 - на первой кости выпало1очко и B2 - на второй кости выпало 1
очко
P(X=2) = P(A2)P(B2) ⇒ P(X=2) =(1\6)·(1\6) = 1\36 .
2. X=3, A31=на первой кости выпало 1 очко и B31=на второй кости выпало 2
очка или A32=на первой кости выпало 2 очка и B22=на второй кости выпало
1 очко.
P(X=3)=P(A31)P(B31) + P(A32)P(B32) = (1\6)·(1\6) + (1\6)·(1\6) = 2\ 36 .
54.
3. X = 4, A41=на первой кости выпало 1 очко и B41=на второй кости выпало3 очка или A42=на первой кости выпало 2 очка и B42=на второй кости
выпало 2 очка или A43=на первой кости выпало 3 очка и B43=на второй
кости выпало 1 очко.
P(X = 3) = P(A31)P(B31) + P(A32)P(B32) ⇒ P(X = 3) = (1\6)·(1\6) + (1\6)·(1\6)
= 2\ 36 .
Продолжив разбор вариантов выпадения очков для каждого значения
суммы аналогичным образом, получим таблицу закона распределения для
изучаемой случайной величины X:
55.
56.
Замечание. Следует заметить, что эту задачу можно было бы решить созначительно меньшими усилиями, если рассматривать искомую случайную
величину X как сумму двух случайных величин X1 и X2, каждая из которых
представляет число выпавших очков на соответствующем кубике.





















































 Математика
Математика








