Системы счисления(СС). Лекция 2

1.

Лекция 2
Системы счисления(СС).
Учебные вопросы.
1. Системы счисления и их
классификация.
2. Двоичная, восьмеричная и
шестнадцатеричная СС.
3. Перевод чисел из одной СС в другую.

2.

1.Системы счисления и их классификация.
Система счисления(СС) — это способ изображения чисел с помощью
базисных символов, имеющих определенные количественные значения.
СС делятся на позиционные и непозиционные.
Основанием позиционной СС называется количество различных
базисных цифр, используемых для изображения числа.
В современном мире широко распространена десятичная позиционная
система счисления, которая представлена десятью базисными числами:
0,1,2,3,4,5,6.7,8,9.
В непозиционной римской системе счисления базисными являются числа
1, 5, 10, 50, 100, 500, 1000 с соответствующими знаковыми обозначениями: I,
V, X, L, C, D, M. При этом другие числа получаются сложением или
вычитанием базисного числа по следующему алгоритму: - если цифра справа
меньше или равна цифре слева, то эти цифры складываются; - если цифра
слева меньше, чем цифра справа то левая цифра вычитается из правой. Так,
например число 146 в римской системе счисления имеет вид: CXLVI, где С 100, XL -40, VI - 6.
Если Р - основание позиционной системы счисления, то любое дробное число
А аm am 1...a1a0 , a 1a 2 ..a s
представляется в виде многочлена вида
A am P m am 1 P m 1 ... a1 P1 a0 P 0 a 1 P 1 a 2 P 2 ...a s P s (1)
где символы ак обозначают любые базисные числа СС с основанием Р.

3.

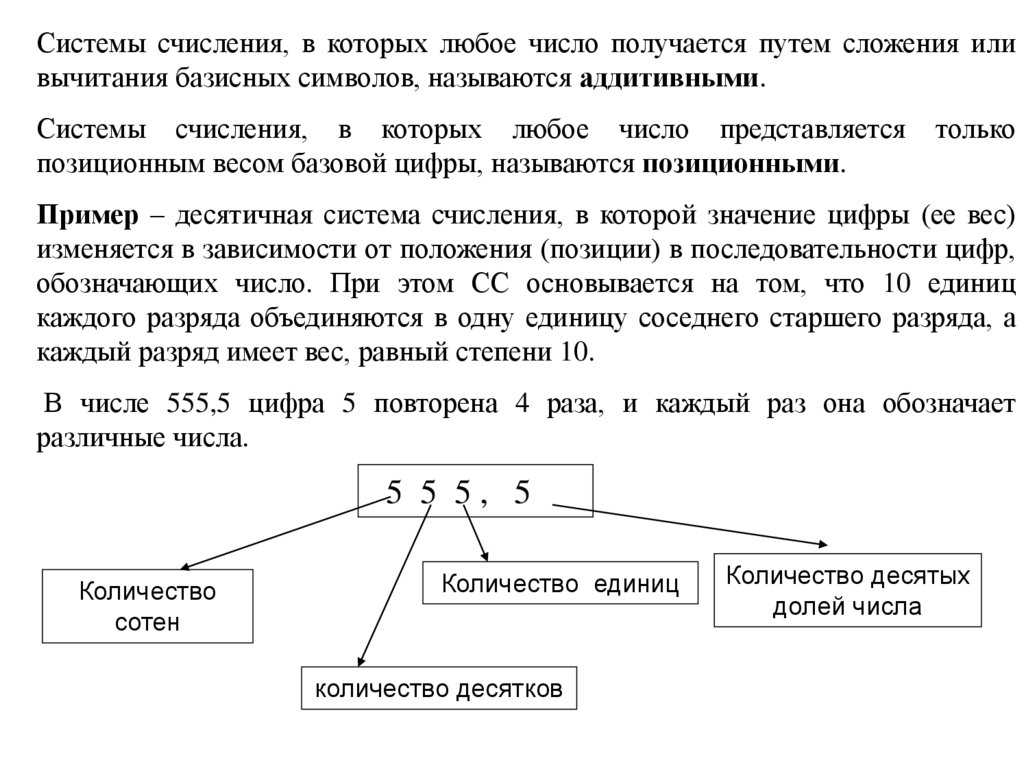
Системы счисления, в которых любое число получается путем сложения или
вычитания базисных символов, называются аддитивными.
Системы счисления, в которых любое число представляется
позиционным весом базовой цифры, называются позиционными.
только
Пример – десятичная система счисления, в которой значение цифры (ее вес)
изменяется в зависимости от положения (позиции) в последовательности цифр,
обозначающих число. При этом СС основывается на том, что 10 единиц
каждого разряда объединяются в одну единицу соседнего старшего разряда, а
каждый разряд имеет вес, равный степени 10.
В числе 555,5 цифра 5 повторена 4 раза, и каждый раз она обозначает
различные числа.
5 5 5, 5
Количество
сотен
Количество единиц
количество десятков
Количество десятых
долей числа

4.

В десятичной СС Р=10 и формула (1) принимает вид
A am 10 m am 1 10 m 1 ... a1 101 a0 100 a 1 10 1 a 2 10 2 ...a s 10 s
(2)
Пример. Представление десятичного числа 286,34 в десятичной СС по
формуле (2) имеет вид:
286,34 = 2 • 102 + 8 •101 + 6 •100 + 3 •10-1 + 4 • 10-2
С фиксированной запятой все числа изображаются в виде
последовательности цифр с постоянным положением запятой для всех чисел.
Пример. Если на целую часть числа отводится четыре позиции, а на
дробную – три, то записи десятичных чисел 23,237, 1021,26 соответственно
имеют вид 0023,237 и 1021,260.
Если на целую часть числа отведено m разрядов, а на дробную - s, то в
системе с основанием Р числа А с фиксированной запятой можно изобразить (без
учета знака) в пределах Р-s <А<Рm –Р-s. При P=2, m=10, s=6 имеем неравенство
0,015< А<1024.
С плавающей запятой число представляется в виде двух групп чисел —
мантиссы и порядка, причем абсолютная величина мантиссы, как правило,
меньше 1, а порядок - целое число.
В общем виде число А записывается в виде А =± М • Р±r, где М мантисса, r - порядок числа, Р - основание СС.

5.

Пример. Представление десятичных чисел 720 и -0,00201 с плавающей
запятой: 720=0,72 •103 и - 0,00201 = - 0,201 •10-2.
Диапазон для чисел с плавающей запятой при отведении m разрядов для
мантиссы и s разрядов для порядка без учета запятой задается неравенствами
(2)
P
m
P
( P s 1)
A (1 P
m
)P
( P s 1)
При Р=2, m=10 и s=6 согласно (2) диапазон чисел с плавающей запятой в
ПК составляет примерно от 10–19 до 1019. Этого вполне достаточно для
практических расчетов.
2. Двоичная, восьмеричная,
шестнадцатеричная и смешанная СС.
В двоичной системе счисления для изображения числа используются
только две базисные цифры 0 и 1. При этом перевод числа в старший разряд при
выполнении вычислений производится при получении числа 2, а в десятичной
СС - числа 10.

6.

В двоичной СС число А а m a m 1...a1a 0 , a 1a 2 ..a s по формуле (2)
записывается следующим образом
A a m 2 m a m 1 2 m 1 ... a1 21 a 0 20 a 1 2 1 a 2 2 2 ...a s 2 s ,
где каждый коэффициент а к может быть одним из базисных чисел 0 или 1.
Изображения чисел десятичной системы в двоичной системе при
отведении четырех позиций на число имеет вид:
000002
1-00012
2-00102
3-00112
4-01002
5-01012
6-01102
7-01112
8-10002
9-10012
где цифрой 2 при значении каждого числа указана его система счисления.
Таблица сложений в двоичной СС :
0+0=0
1+0=1
0+1=1
1+1=10
Таблица умножения в двоичной СС :
0х0=0
1х0=0
0х1=0
1х1=1
В двоичной системе счислений при изображении любого числа
используются только две цифры 0, 1 и арифметические действия очень просты,
поэтому современные ЭВМ используют для кодировки информации двоичную
систему счислений, так как все электронные элементы памяти ЭВМ могут
находиться, только в дух состояниях: включено - 1 или выключено - 0.

7.

Пример. Представление двоичного числа 101110,1012 в двоичной СС по
формуле (1):
101110,1012 = 1• 25 + 0 • 24 +1 • 23 +1 • 22 +1 • 21 + 0 • 20 +1 • 2-1 + 0 • 2-2 +
+1 • 2-3 = 46,62510.
Неудобство использования двоичной системы счисления из-за
громоздкости записи чисел, особенно при разработке программ на машинном
языке привели к использованию восьмеричной и шестнадцатеричной систем
счисления.
В восьмеричной СС базовыми цифрами являются: 0, 1, 2, 3, 4, 5, 6, 7
Число А аm am 1...a1a0 , a 1a 2 ..a s в восьмеричной системе счисления
будет представлено в виде многочлена:
A am 8m am 1 8m 1 ... a1 81 a0 80 a 1 8 1 a 2 8 2 ...a s 8 s
Пример. Число 8310 десятичной системы можно представить
следующим образом:
8310 = 64+16+3= 1 • 82 +2 • 81 +3 • 80=1238.
В шестнадцатеричной системе базисными являются цифры от 0 до
15. В этой системе для обозначения всех базисных цифр не хватает цифр
десятичной системы, поэтому для обозначения первых десяти цифр
используют цифры десятичной системы от 0 до 9, а для обозначения
последующих шести цифр используют буквы A,B.C,D,E,F, причем

8.

A=10,
B=11, C= 12,
представлены в таблице
A-10102
вид:
B-10112
D=13,
C-11002
E=14,
F=15. Двоичные коды этих чисел
D-11012
E-11102
F-11112
Пример. Десятичное число 175,510 в шестнадцатеричной системе имеет
175,510= 10 • 161 + 15 •160 + 8 • 16-1 = AF,816.
Часто числа, заданные в одной СС приходится изображать с помощью
цифр другой. Например, десятичные числа переводятся в двоичные, с которыми
работает ЭВМ. В этих случаях используются смешанные системы счисления, в
которых каждая цифра числа в СС с основанием Р записывается
соответствующими кодами из базисных цифр в СС с основанием Q. В такой
системе P называется старшим основанием, а Q - младшим основанием. Для того,
чтобы запись числа в смешанной системе счисления была однозначной, для
представления цифры в СС с основанием Р отводится одно и то же количество
разрядов СС с основанием Q, достаточное для представления максимального
значения базовых чисел исходной системы.
Для изображения числа в смешанной двоично-десятичной системе
отводятся четыре двоичных разряда, а, например десятичное число 92510 в
двоично-десятичной системе запишется в виде: 1001 0010 01012.

9.

где последовательные тетрады (четверки) двоичных чисел изображают цифры
9,2,5 записи числа в десятичной СС. При этом для записи максимального числа
десятичной системы 9 требуется четыре двоичных разряда, следовательно, и
остальные числа этой же десятичной системы должны быть представлены
четырьмя разрядами двоичных чисел.
3.Перевод чисел из одной СС в другую.
При переводе чисел из СС с основанием Р в десятичную систему
счисления используют разложение (1), а затем выполняют арифметические
операции в десятичной системе счисления..
Пример.
1.Перевод числа двоичной СС в десятичную : 101, 112=1 • 22+0 •21+1 • 20+
+1 • 2-1+1 • 2-2=4+1+0,5+0,25=5,7510.
1.Перевод числа восьмеричной СС в десятичную : 3718= 3 • 82+7 •81+1 • 80=
24910
2.Перевод числа шестнадцатеричной СС в десятичную : АF,416=10 •161+
3.+15 •160+ 4 •16-1=175,2510.

10.

При обратном переводе целые и дробные части числа переводятся
отдельно.
Перевод целых чисел из десятичной системы в систему счисления с
основанием Р
производится делением числа и получаемых частных на
основание Р. Процесс деления прекращается, когда очередное частное станет
меньше, чем основание СС Р.
Пример. Перевести десятичное число 9810 в двоичную систему счисления Р=2.
98:2=49
остаток 0
(49х2=98)
49:2=24
остаток 1 (2х24=48)
24:2=12
остаток 0 (2х12=24)
12:2=6
остаток 0 (2х6=12)
6:2=3
остаток 0 (3х2=6)
3:2=1
остаток 1 (2х1=2)
1:2=0
Подчеркнутые остатки и последнее частное, записанные в обратном
порядке, составляют двоичное числа в двоичной СС: 9810=11000102. Проверка
осуществляется выполнением обратной операции:

11.

11000102= 1• 26 + 1 • 25 +0 • 24 +0 • 23 +0 • 22 + 1 • 21 +0 • 20=9810.
Перевод дробной части числа. Для
перевода
дробной
части
десятичного числа в СС с основанием Р необходимо дробною часть умножать на
Р, выделяя целую часть m-число раз, пока не будет достигнута заданная точность.
Пример. Перевод дроби 0,62510 из десятичной системы счисления в двоичную.
Решение:
Таким образом, двоичное число записываем сверху вниз
из цифр в целой части, показанной заливкой:
0,1012
0,
625 • 2
Проверяем результат:
-1 +0 •2-2+1 •2-3=0,5+0,125=0,625.
0,101
=1
•2
2
1,
250 • 2
0,
5•2
1
0•2