Сложение и вычитание векторов

1.

Сложение
и
вычитание
векторов

2.

Перемещение из одной точки в другую
может быть различным
Дом
Школа
Левый берег
Тверцы

3.

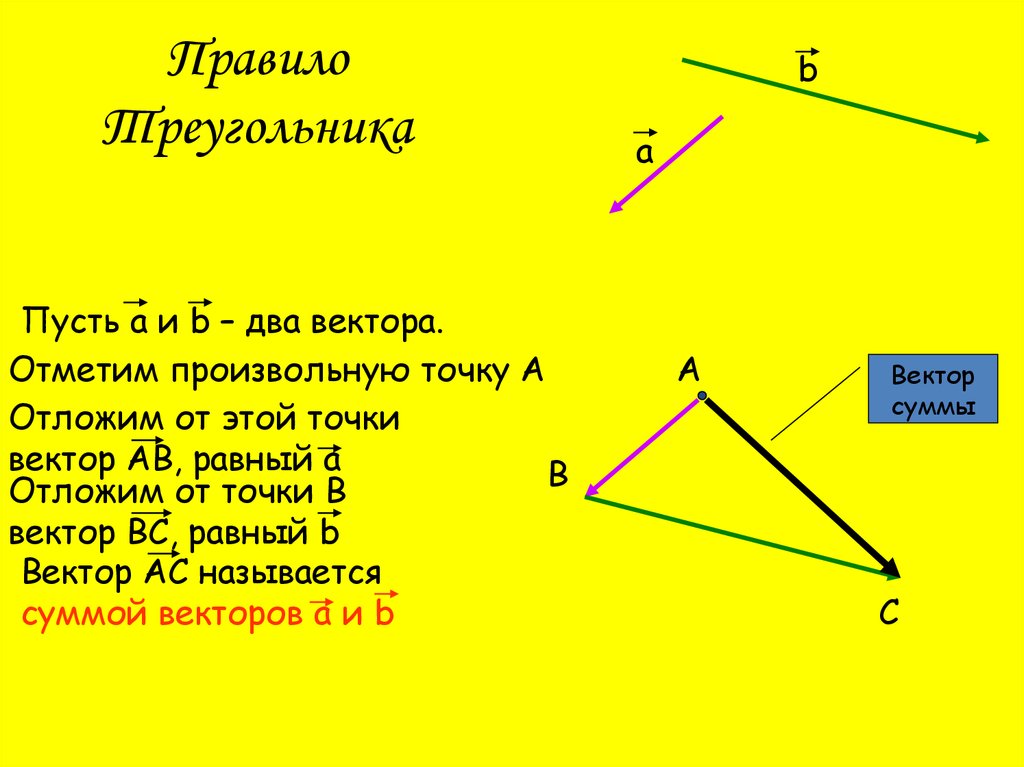
Правило
Треугольника
Пусть а и b – два вектора.
Отметим произвольную точку А
Отложим от этой точки
вектор АВ, равный а
В
Отложим от точки В
вектор ВС, равный b
Вектор АС называется
суммой векторов а и b
b
а
А
Вектор
суммы
C

4.

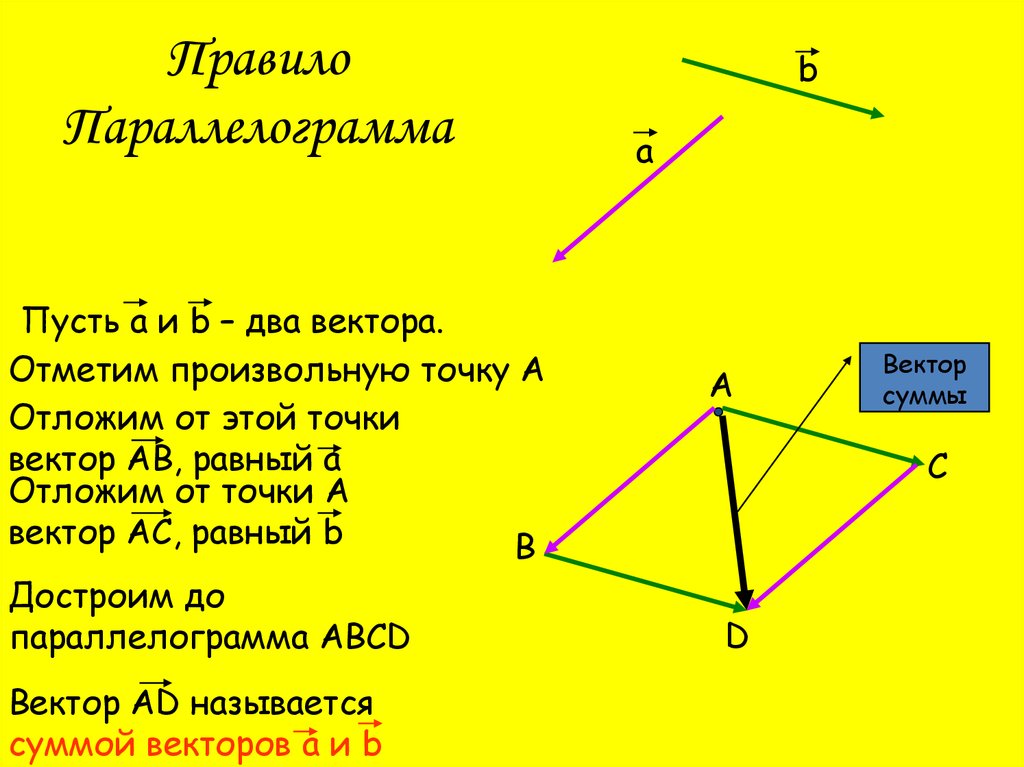
Правило
Параллелограмма
Пусть а и b – два вектора.
Отметим произвольную точку А
Отложим от этой точки
вектор АВ, равный а
Отложим от точки А
вектор АС, равный b
В
Достроим до
параллелограмма АВСD
Вектор АD называется
суммой векторов а и b
b
а
А
Вектор
суммы
C
D

5.

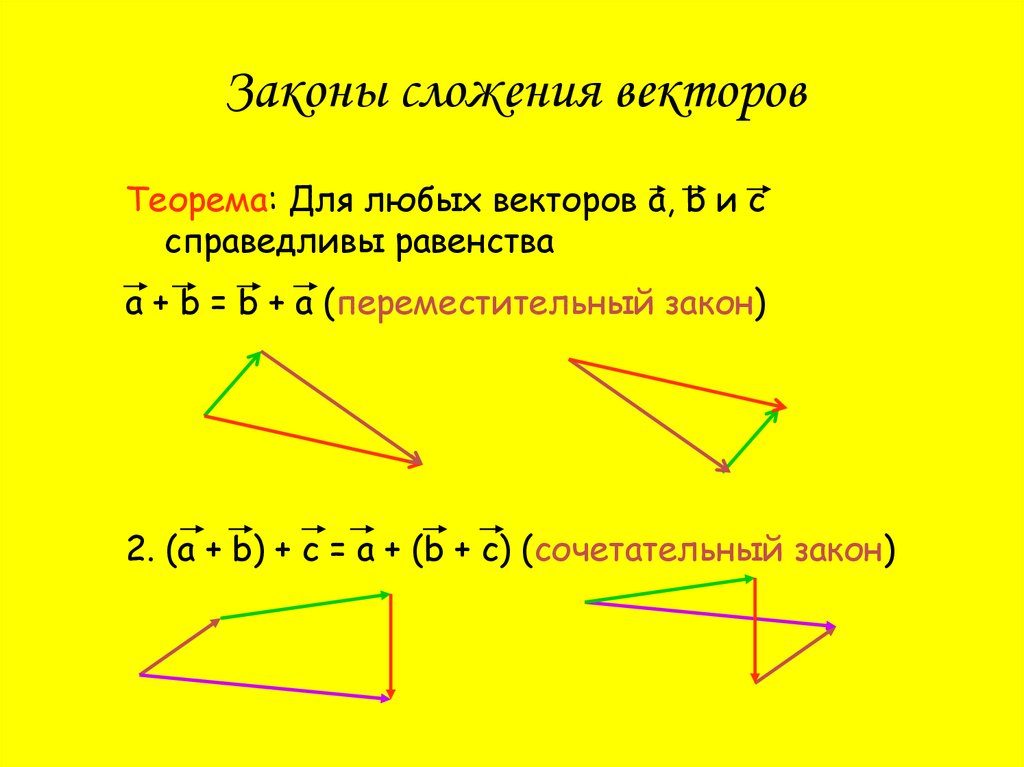
Законы сложения векторов
Теорема: Для любых векторов а, b и с
справедливы равенства
а + b = b + a (переместительный закон)
2. (а + b) + c = a + (b + c) (сочетательный закон)

6. Сложение нескольких векторов

Вектор
суммы

7.

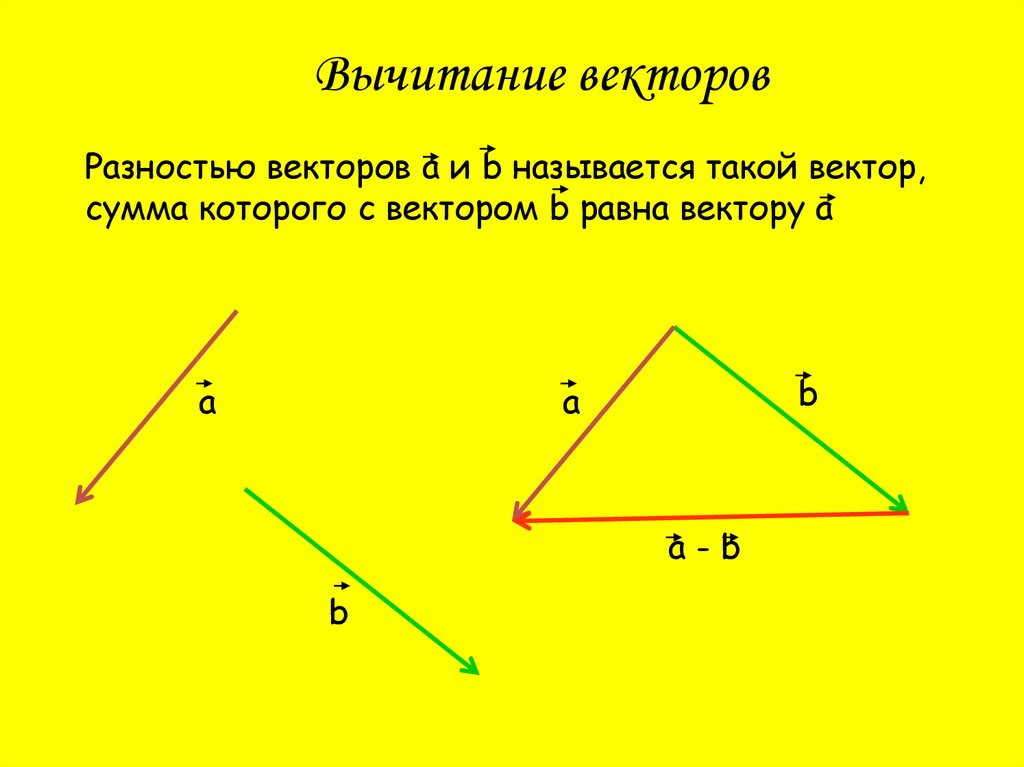
Вычитание векторов
Разностью векторов а и b называется такой вектор,
сумма которого с вектором b равна вектору а
а
b
а
а-b
b

8.

Тест
Вопрос №1 Верно ли, что сумма длин двух
неколлинеарных векторов равна длине их
суммы?
да
нет

9.

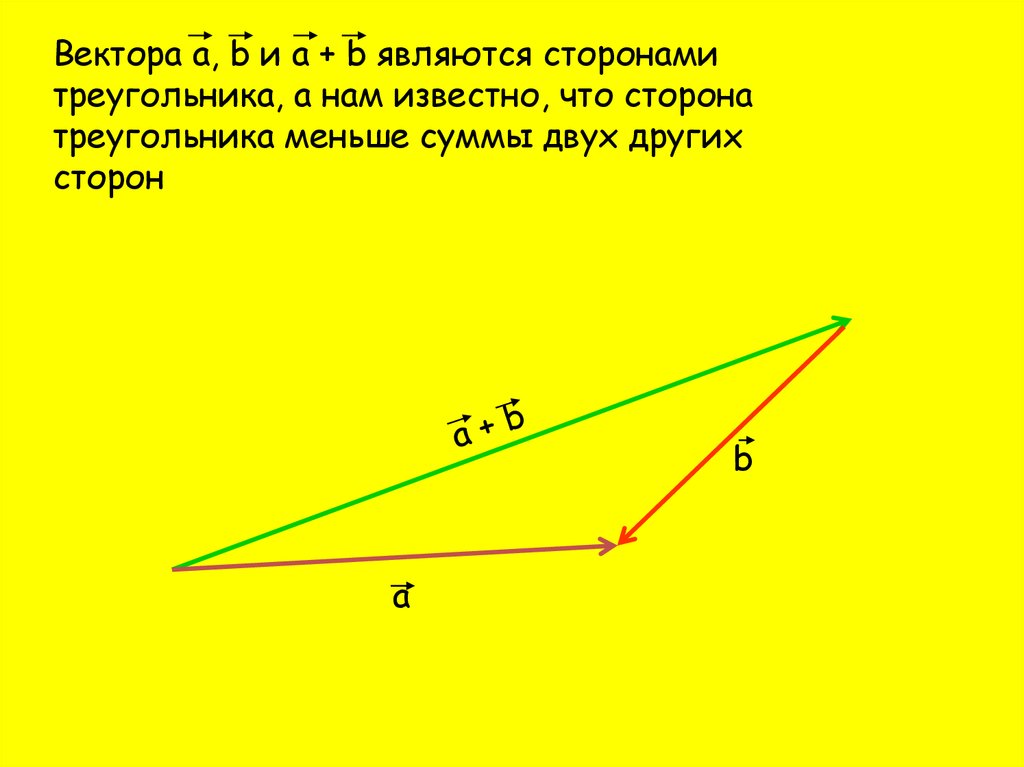
Вектора а, b и а + b являются сторонами
треугольника, а нам известно, что сторона
треугольника меньше суммы двух других
сторон
b
а

10.

Вопрос №2 Может ли сумма нескольких
векторов равняться нулевому вектору?
да
нет

11.

Если начало первого вектора совпадает с концом
последнего вектора, то сумма данных векторов
равна нулевому вектору.

12.

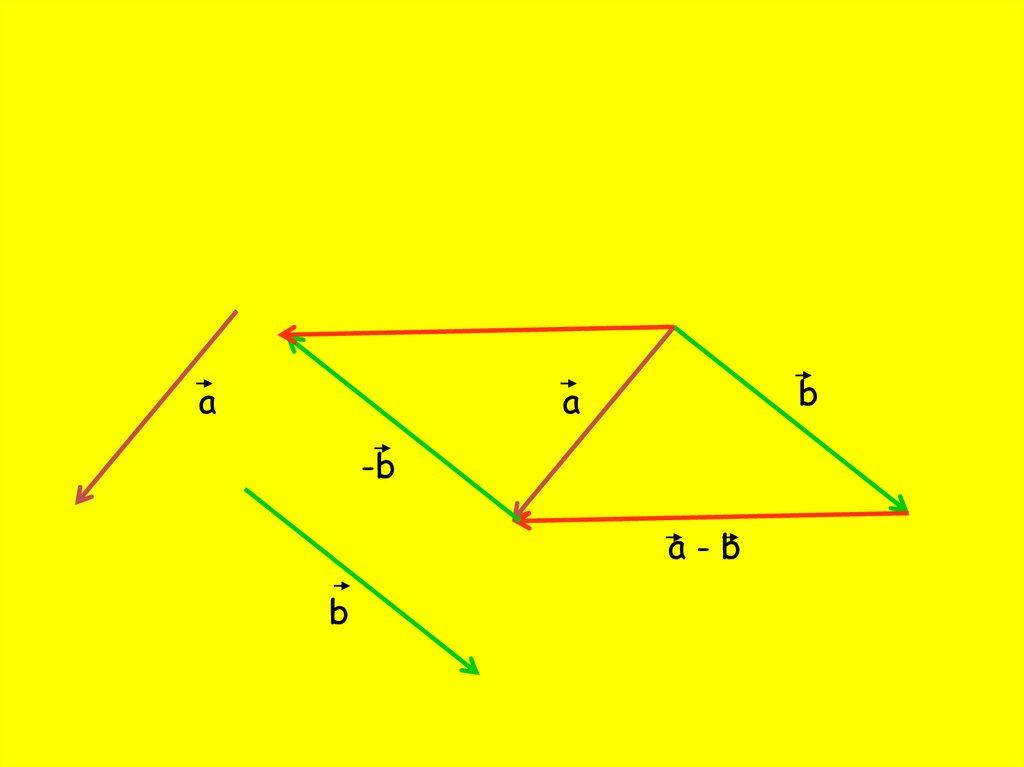
Вопрос №3 Верно ли, что a – b = a + (-b)?
да
нет

13.

а
b
а
-b
а-b
b