Похожие презентации:
Свойства логических операций. Законы алгебры логики
1.
2.
1. Переместительный закон2. Сочетательный закон
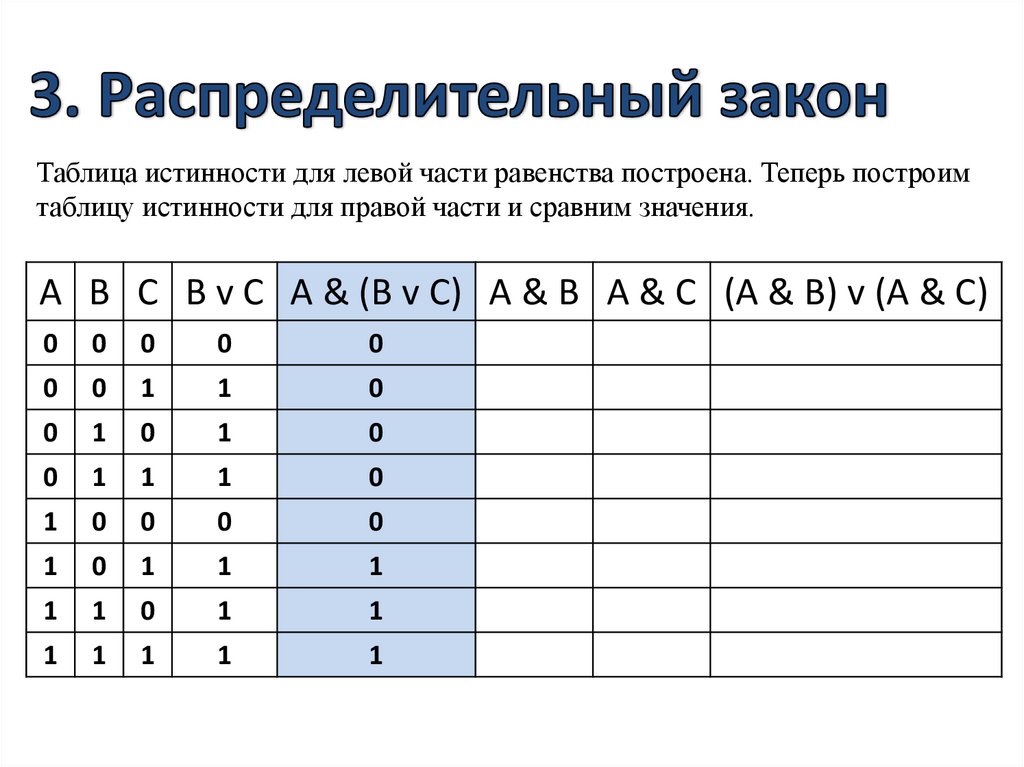
3. Распределительный закон
4. Закон двойного отрицания
5. Закон исключенного третьего
6. Закон повторения
7. Законы операций с 0 и 1
8. Законы общей инверсии (законы де Моргана)
3.
• Для логического умножения:A&B=B&A
• Для логического сложения:
AvB=BvA
4.
• Для логического умножения:(A & B) & C = A & (B & C)
• Для логического сложения:
(A v B) v C = A v (B v C)
Вывод: при одинаковых знаках операций скобки
можно ставить произвольно или вообще опускать.
5.
• Для логического умножения:A & (B v C) = (A & B) v (A & C)
• Для логического сложения:
A v (B & C) = (A v B) & (A v C)
6.
Докажем распределительный закон для логического умножения.Для этого построим таблицу истинности:
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
7.
Заполним столбец B v C. Для этого выполним дизъюнкцию(сложение) значений столбцов B и С:
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
8.
Теперь заполним столбец A & (B v C). Для этого выполнимконъюнкцию (умножение) значений столбцов A и (B v С):
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
1
1
0
1
0
0
0
0
1
0
1
1
1
1
1
0
1
1
1
1
1
1
1
9.
Таблица истинности для левой части равенства построена. Теперь построимтаблицу истинности для правой части и сравним значения.
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
1
1
0
1
0
0
0
0
1
0
1
1
1
1
1
0
1
1
1
1
1
1
1
10.
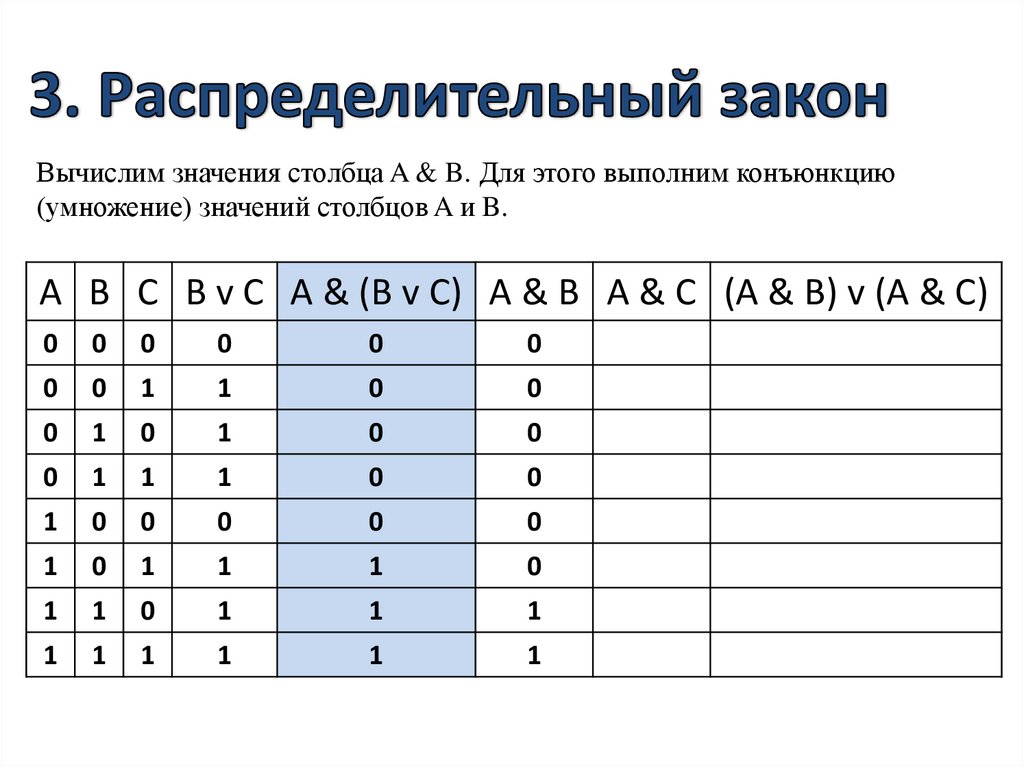
Вычислим значения столбца A & B. Для этого выполним конъюнкцию(умножение) значений столбцов A и B.
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
0
0
1
1
0
0
0
1
0
1
0
0
0
1
1
1
0
0
1
0
0
0
0
0
1
0
1
1
1
0
1
1
0
1
1
1
1
1
1
1
1
1
11.
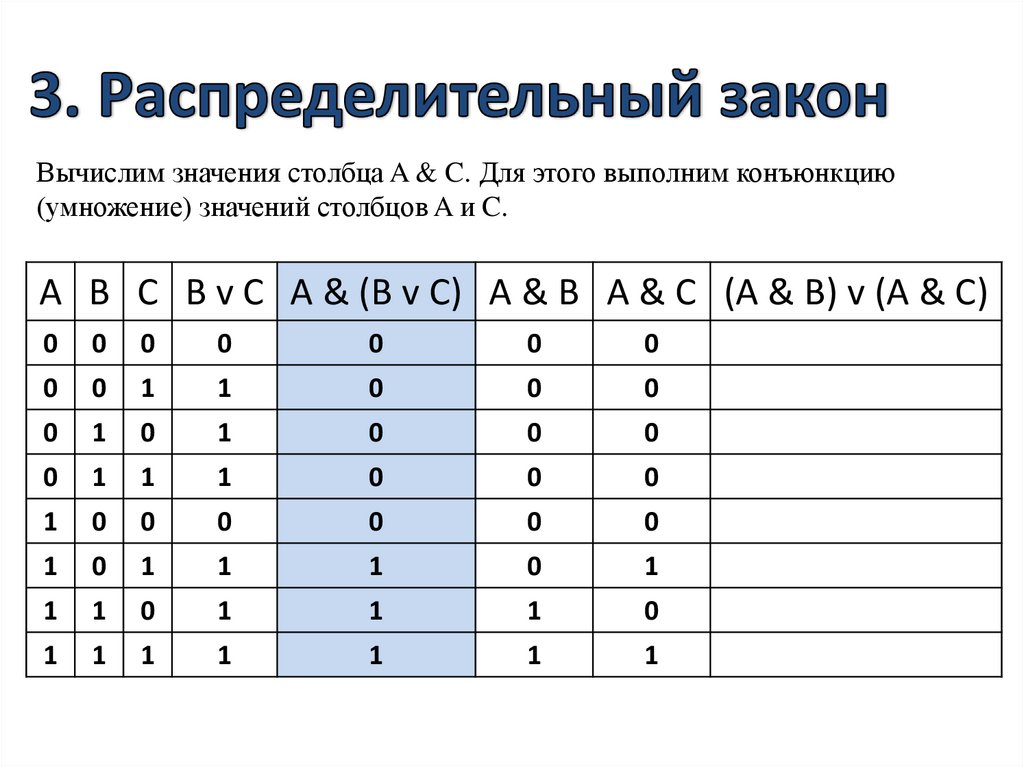
Вычислим значения столбца A & C. Для этого выполним конъюнкцию(умножение) значений столбцов A и C.
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
1
0
1
0
0
0
0
1
1
1
0
0
0
1
0
0
0
0
0
0
1
0
1
1
1
0
1
1
1
0
1
1
1
0
1
1
1
1
1
1
1
12.
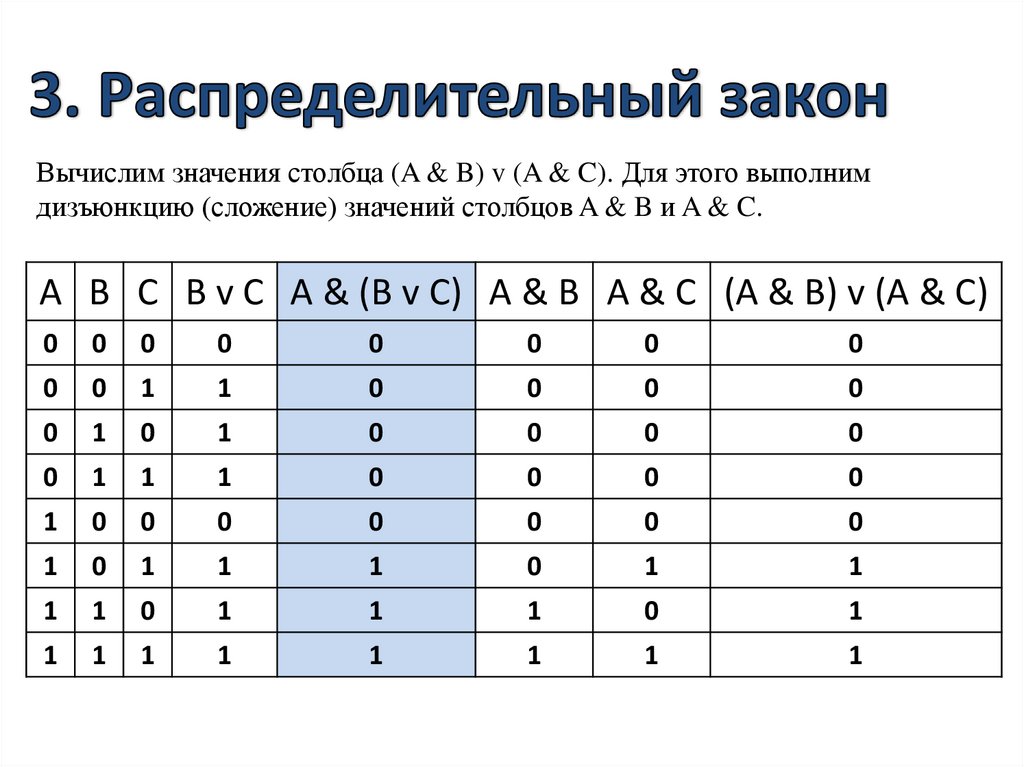
Вычислим значения столбца (A & B) v (A & C). Для этого выполнимдизъюнкцию (сложение) значений столбцов A & B и A & C.
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
1
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
1
1
0
1
1
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
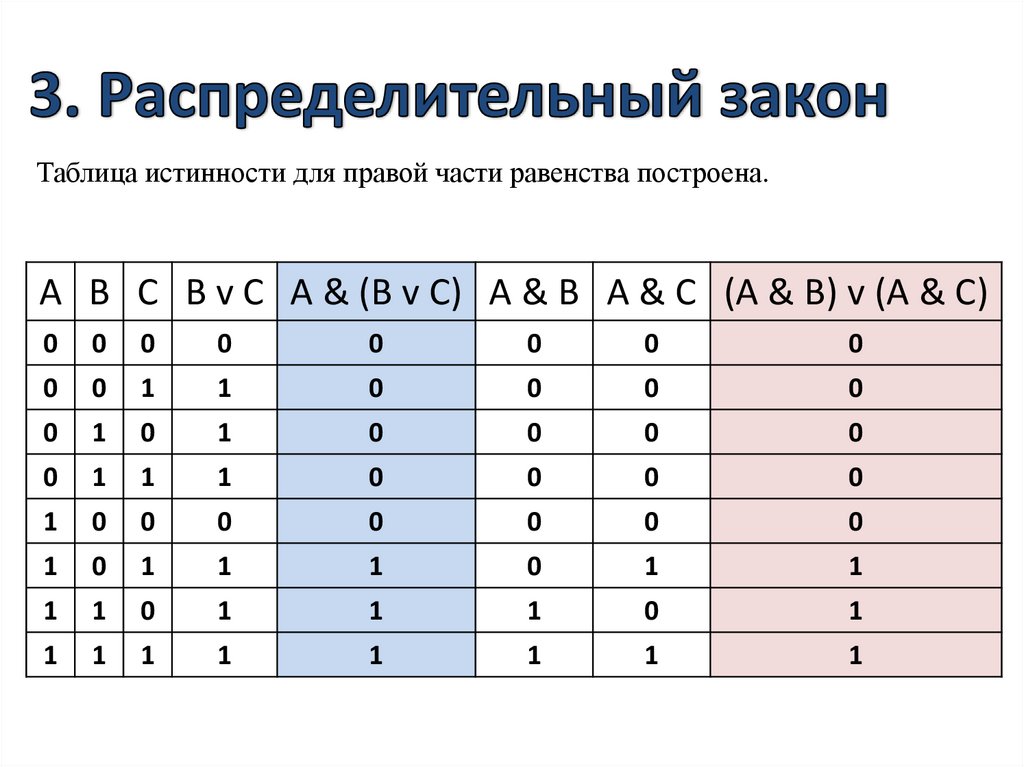
13.
Таблица истинности для правой части равенства построена.A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
1
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
1
1
0
1
1
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
14.
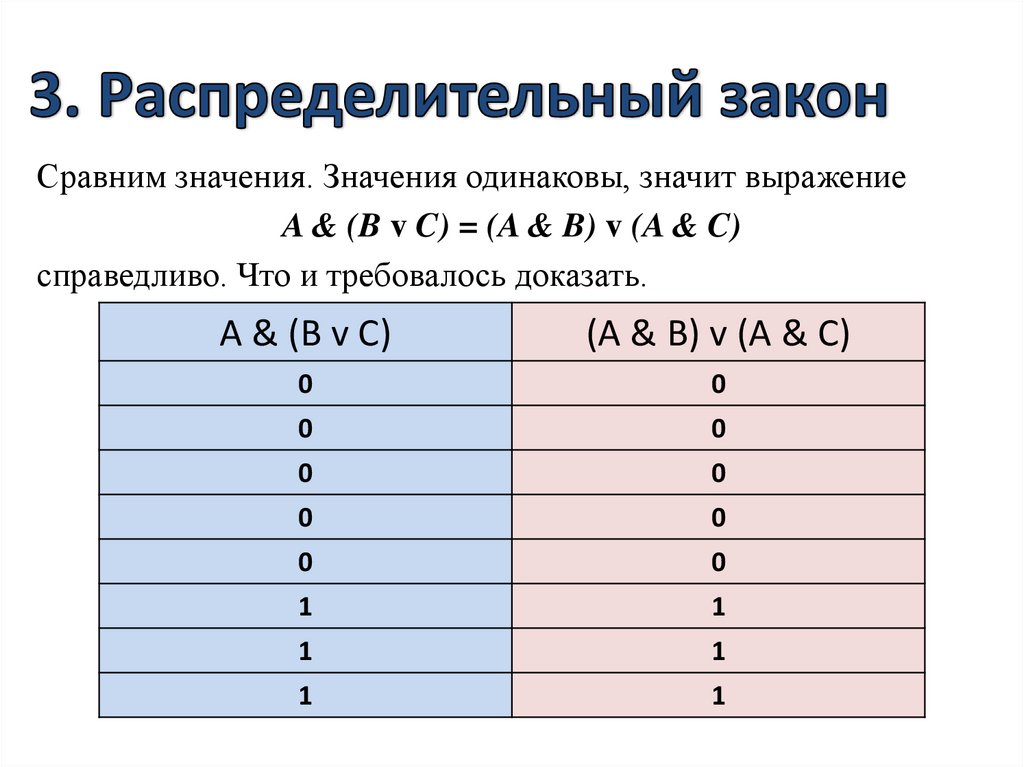
Сравним значения. Значения одинаковы, значит выражениеA & (B v C) = (A & B) v (A & C)
справедливо. Что и требовалось доказать.
A & (B v C)
(A & B) v (A & C)
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
















 Информатика
Информатика