Параллельные прямые в пространстве

1.

Параллельные прямые в
пространстве
Урок геометрии в 10 классе
Автор: Наумова С.В.

2.

РАССМОТРИТЕ КАРТИНКИ И СДЕЛАЙТЕ
ВЫВОД, О ЧЕМ ПОЙДЕТ РЕЧЬ НА УРОКЕ

3.

ТЕМА УРОКА
ПАРА ЛЛЕЛЬНЫЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ
Цели:
Рассмотреть взаимное расположение двух
прямых в пространстве.
Ввести понятие параллельных и
скрещивающихся прямых.
Доказать теоремы о параллельности
прямых и параллельности трех прямых.
Закрепить эти понятия на моделях куба,
призмы, пирамиды.

4.

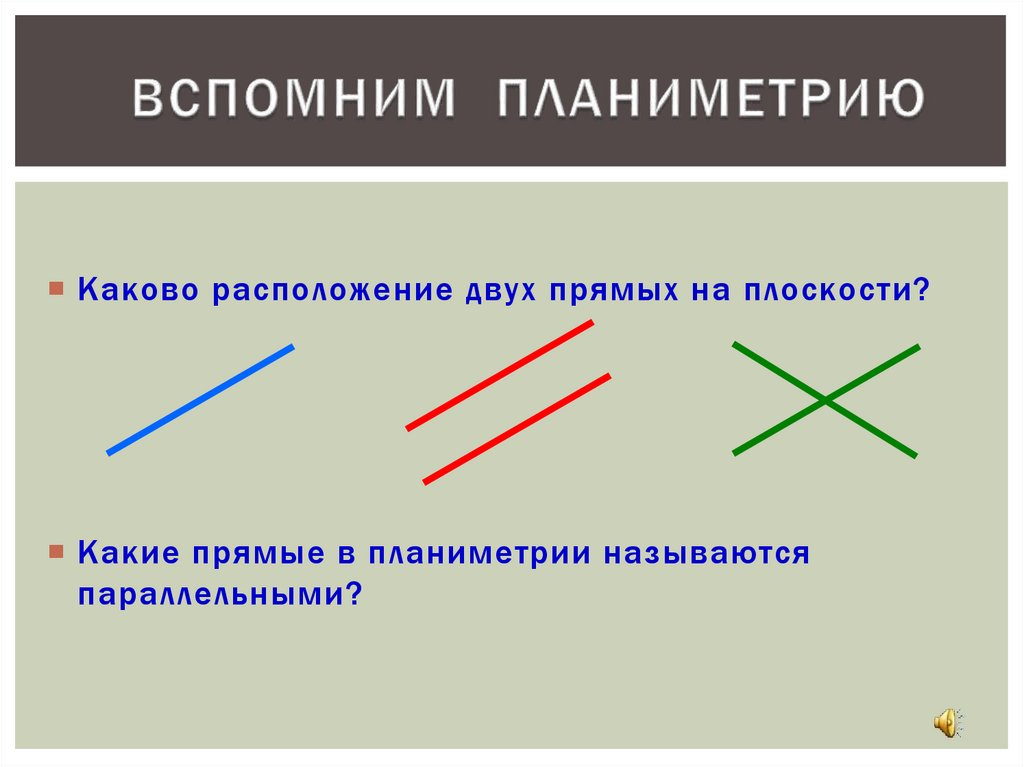
Каково расположение двух прямых на плоскости?
Какие прямые в планиметрии называются
параллельными?

5.

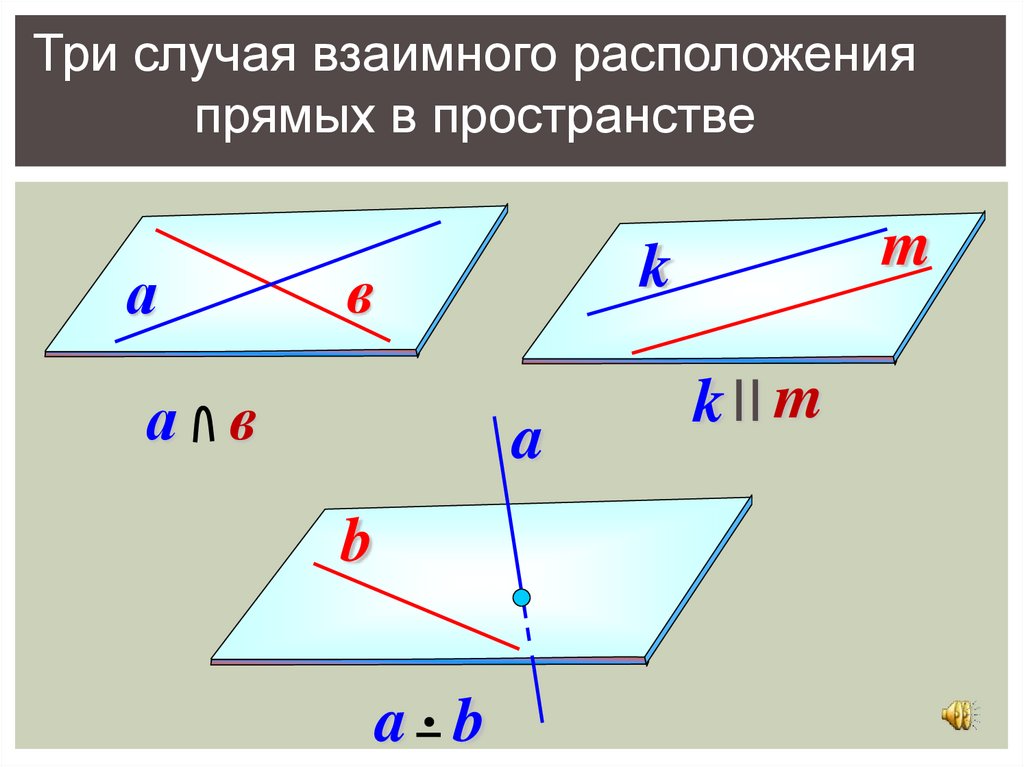
Три случая взаимного расположения
прямых в пространстве
а
m
k
в
а в
a
b
a b
k II m

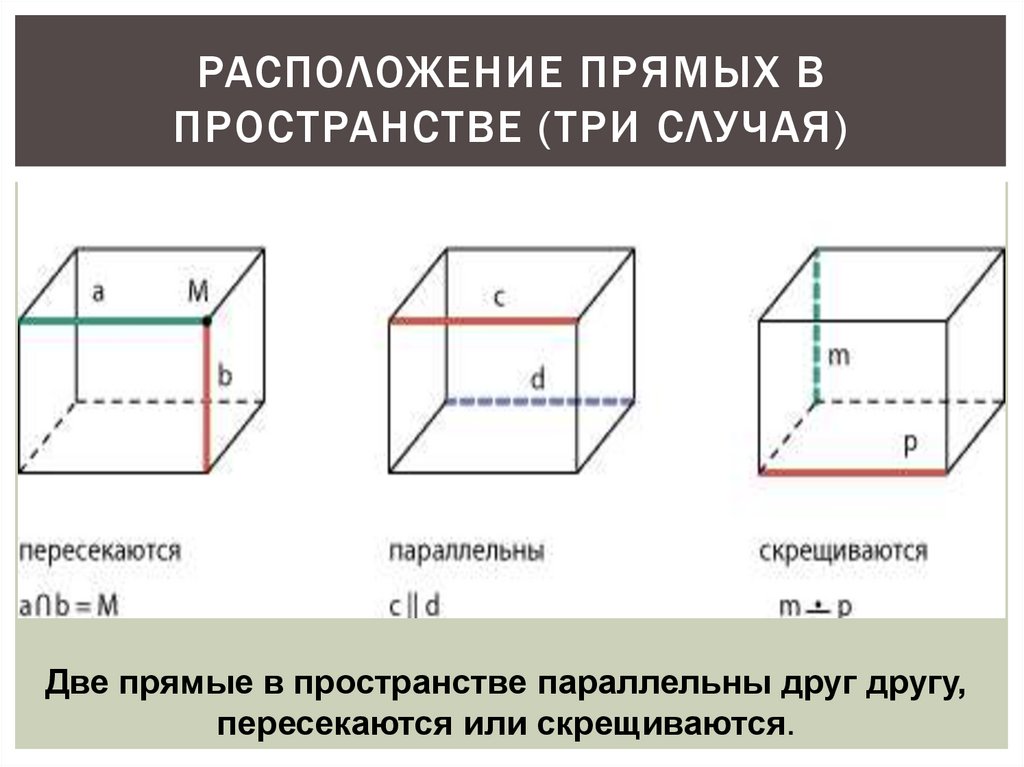
6.

РАСПОЛОЖЕНИЕ ПРЯМЫХ В
ПРОСТРАНСТВЕ (ТРИ СЛУЧАЯ)
Две прямые в пространстве параллельны друг другу,
пересекаются или скрещиваются.

7.

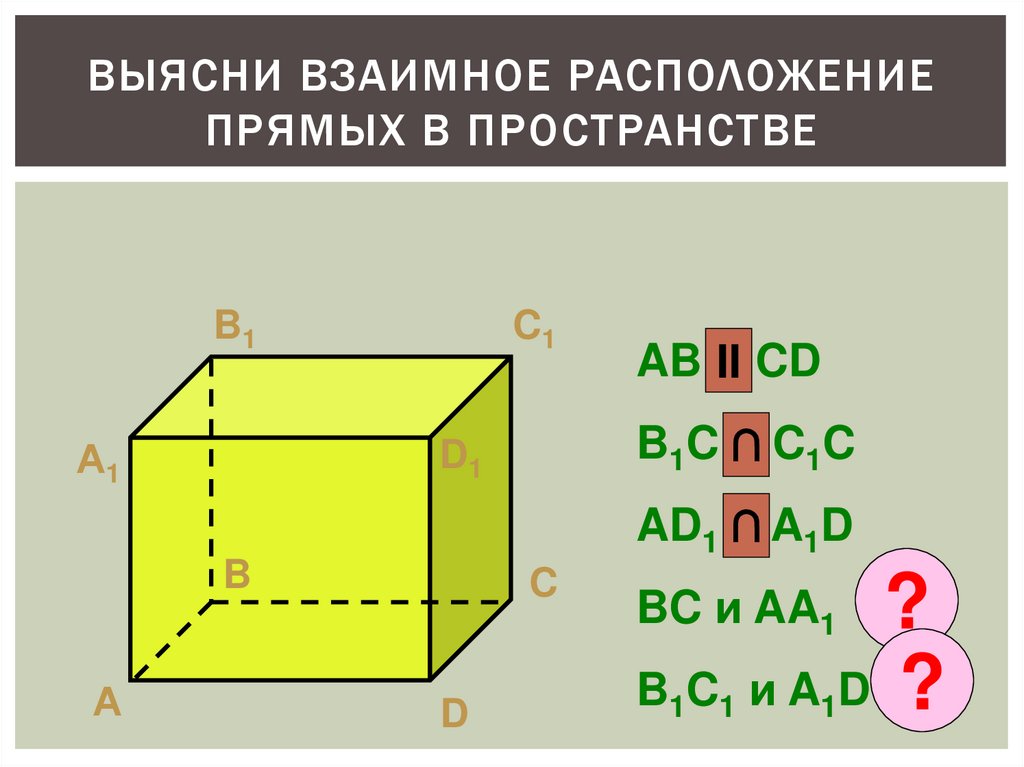
ВЫЯСНИ ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ПРЯМЫХ В ПРОСТРАНСТВЕ
B1
А1
C1
AB и
II CD
B1C ∩
и C 1C
D1
AD1 ∩
и A1D
B
А
C
D
?
B C иA D ?
BC и AA1
1
1
1

8.

КАКИЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ
НАЗЫВАЮТСЯ ПАРА ЛЛЕЛЬНЫМИ?
Определение
Две прямые в пространстве называются
параллельными, если они лежат в одной
плоскости и не пересекаются
a b
, b
a
если
a∩ b

9.

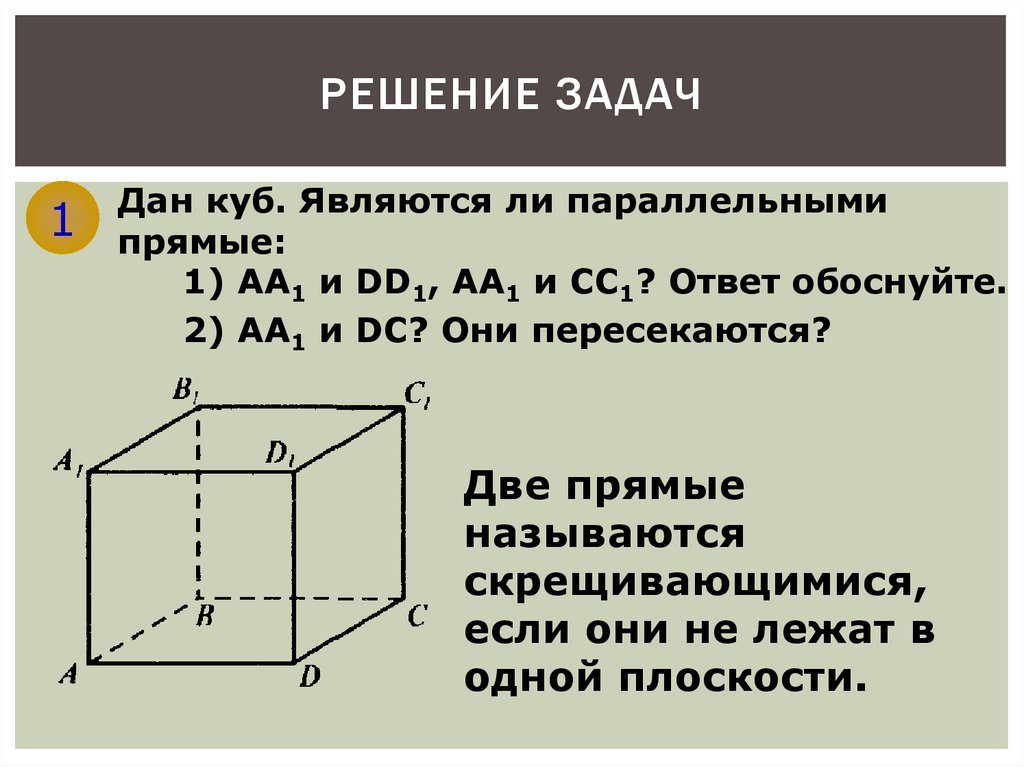
РЕШЕНИЕ ЗАДАЧ
1
Дан куб. Являются ли параллельными
прямые:
1) АА1 и DD1, АА1 и СС1? Ответ обоснуйте.
2) АА1 и DС? Они пересекаются?
Две прямые
называются
скрещивающимися,
если они не лежат в
одной плоскости.

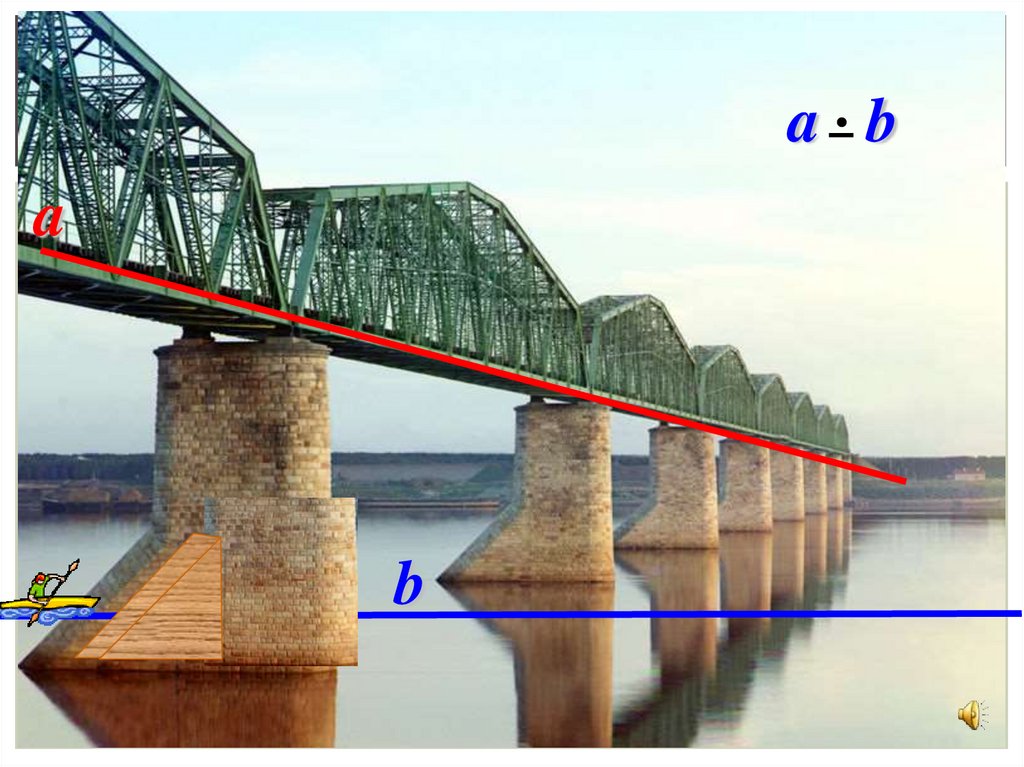
10.

Наглядное представление о скрещивающихся прямых
дают две дороги, одна из которых проходит по
эстакаде, а другая под эстакадой.

11.

a b
a
b

12.

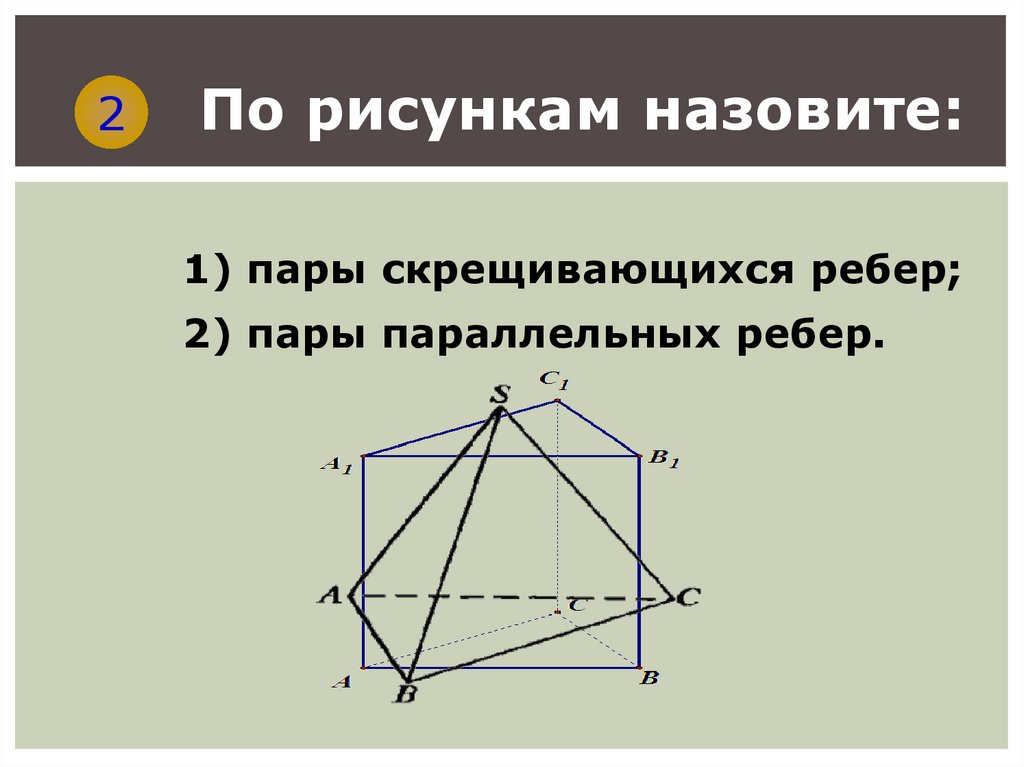
2
По рисункам назовите:
1) пары скрещивающихся ребер;
2) пары параллельных ребер.

13.

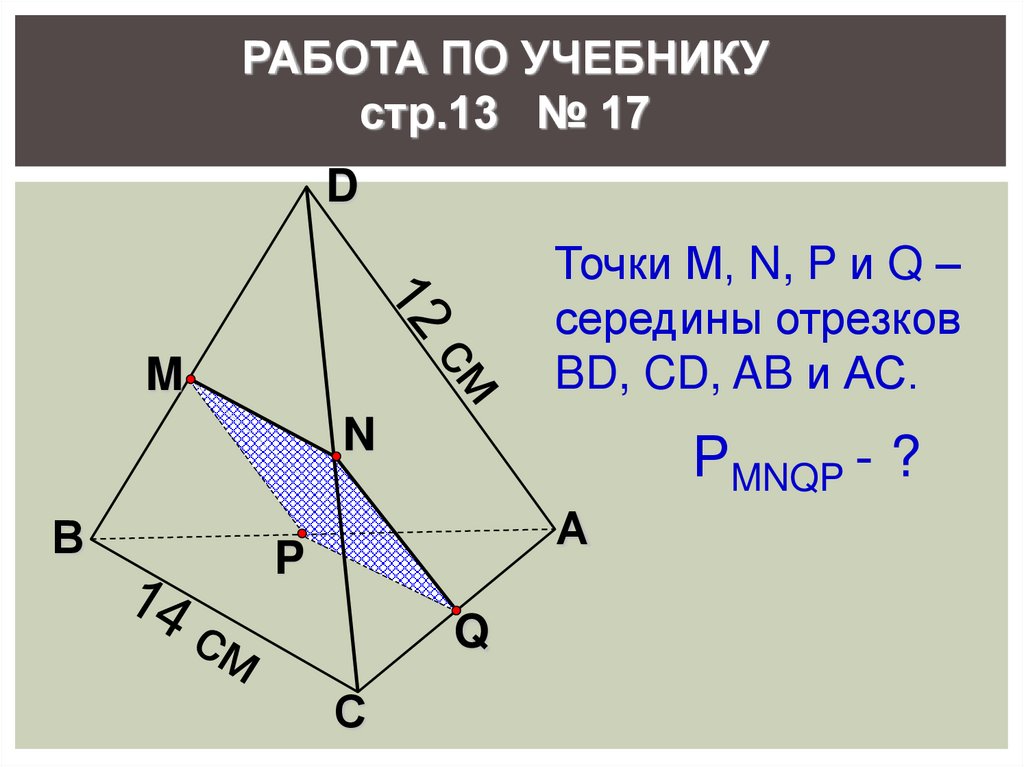
РАБОТА ПО УЧЕБНИКУ
стр.13 № 17
D
Точки М, N, P и Q –
середины отрезков
BD, CD, AB и АС.
M
N
В
РMNQP - ?
А
P
Q
С

14.

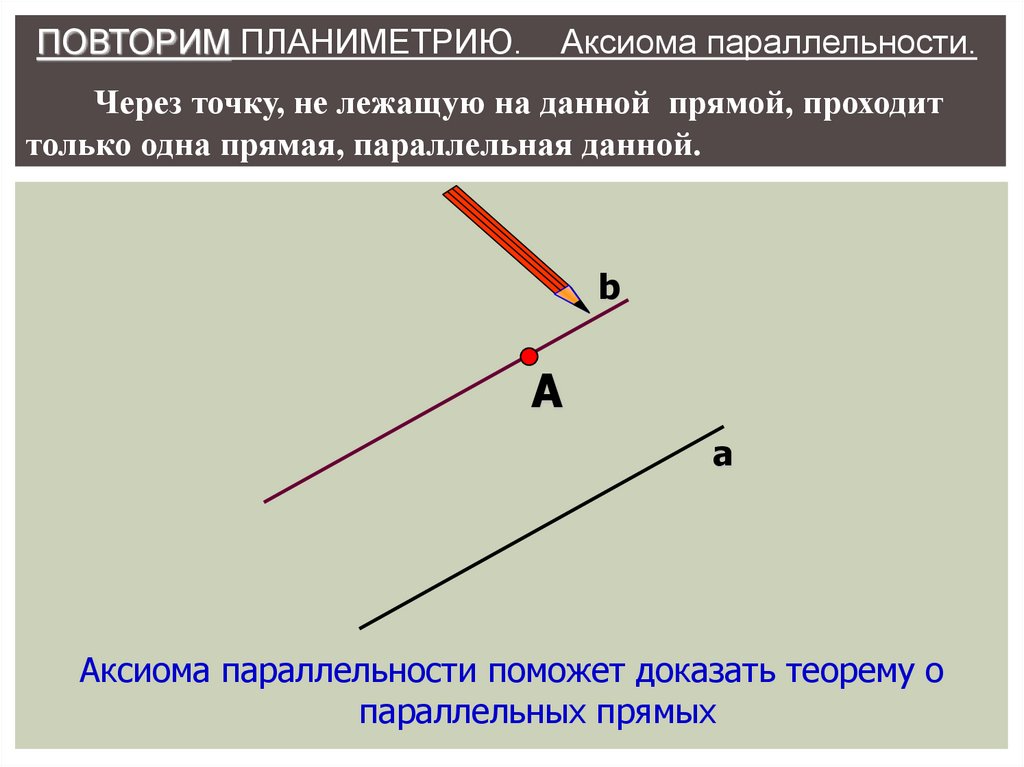
ПОВТОРИМ ПЛАНИМЕТРИЮ.
Аксиома параллельности.
Через точку, не лежащую на данной прямой, проходит
только одна прямая, параллельная данной.
b
А
а
Аксиома параллельности поможет доказать теорему о
параллельных прямых

15.

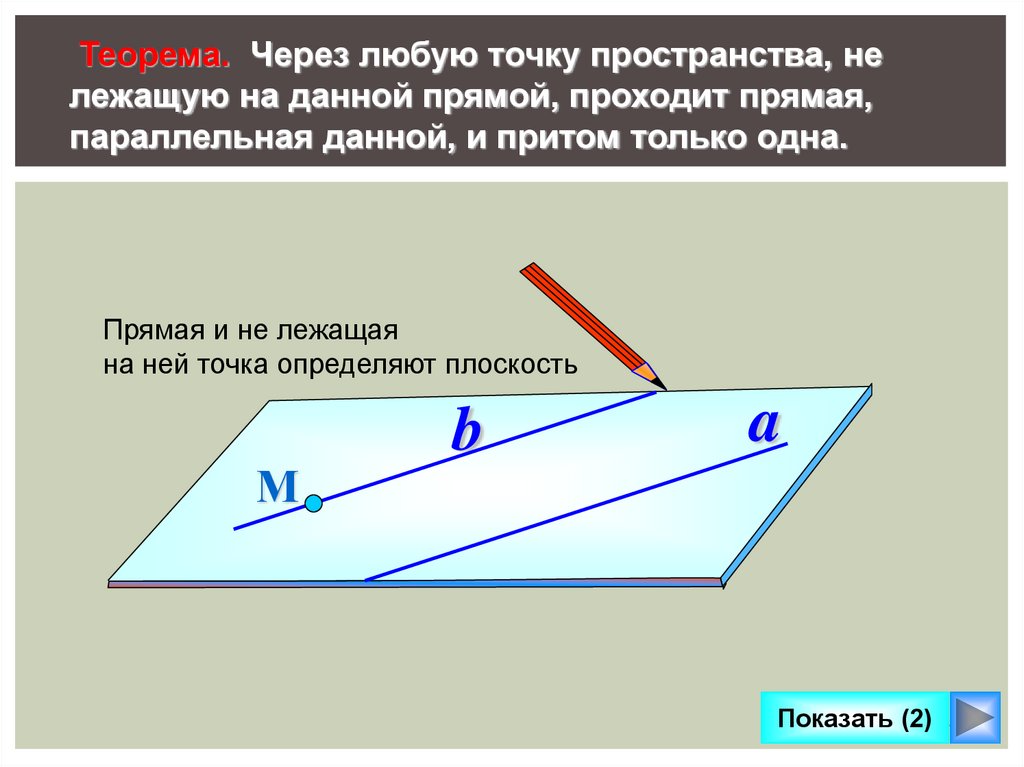
Теорема. Через любую точку пространства, не
лежащую на данной прямой, проходит прямая,
параллельная данной, и притом только одна.
Прямая и не лежащая
на ней точка определяют плоскость
М
b
a
Показать (2) 15

16.

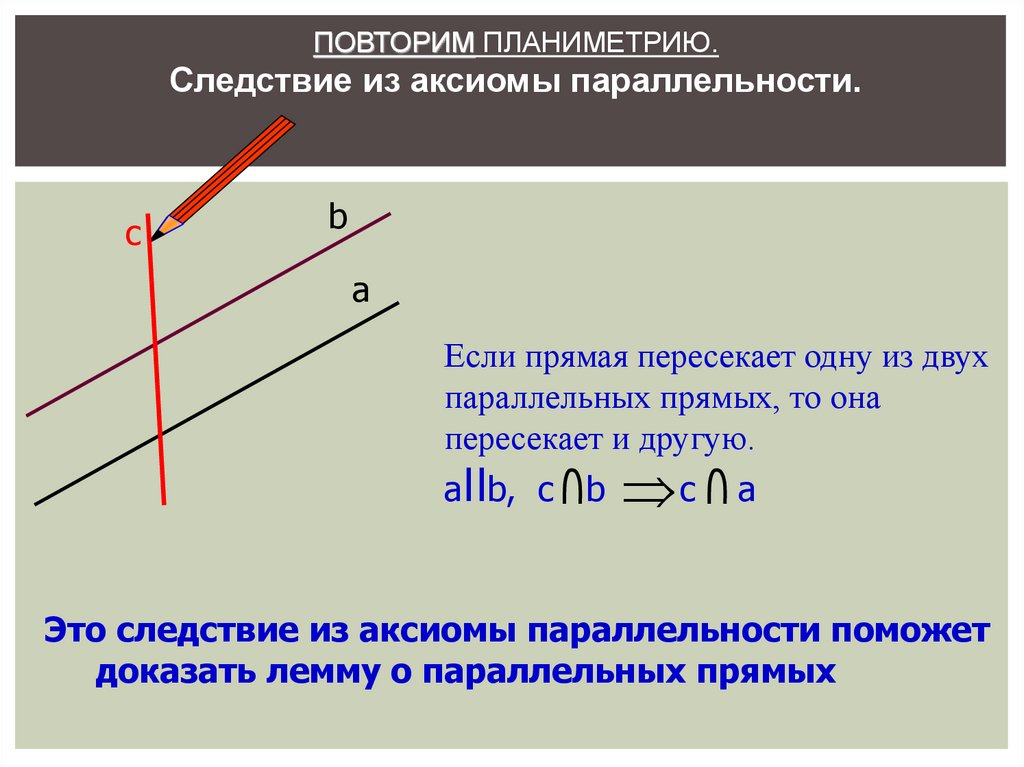
ПОВТОРИМ ПЛАНИМЕТРИЮ.
Следствие из аксиомы параллельности.
c
b
а
Если прямая пересекает одну из двух
параллельных прямых, то она
пересекает и другую.
aIIb, c b
c
a
Это следствие из аксиомы параллельности поможет
доказать лемму о параллельных прямых

17.

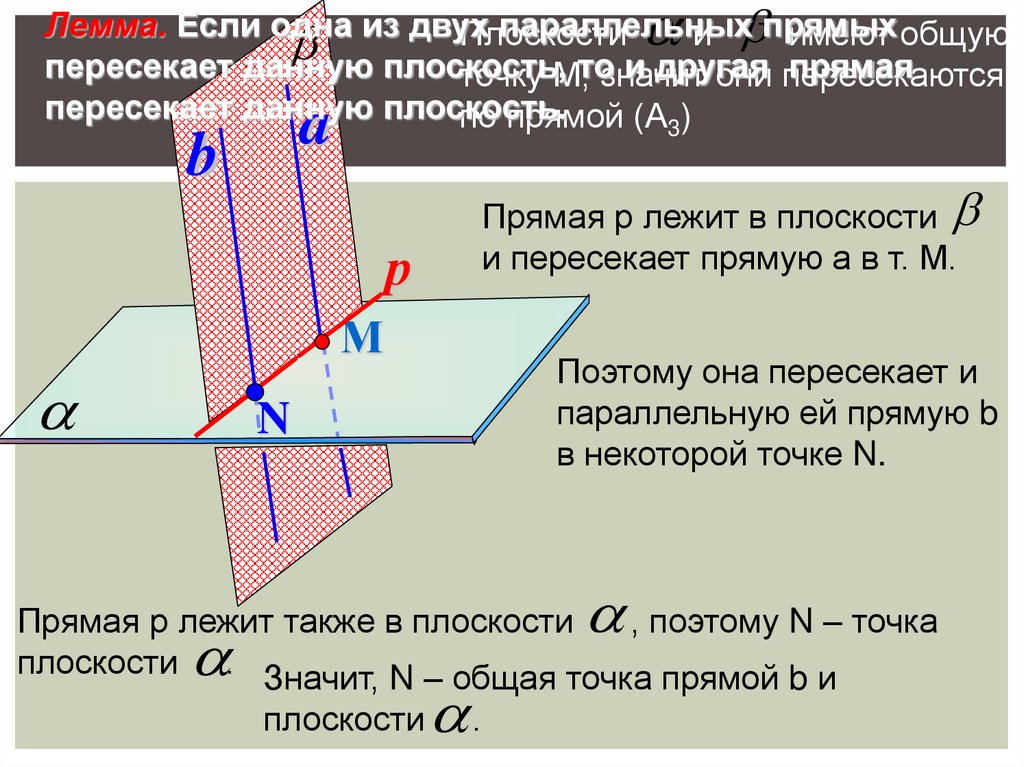
Лемма. Если одна из двух
параллельных
прямых
Плоскости
и
имеют общую
пересекает данную плоскость,
и другая
прямая
точку М,тозначит
они пересекаются
пересекает данную плоскость.
по прямой (А3)
a
b
Прямая р лежит в плоскости
и пересекает прямую а в т. М.
р
М
Поэтому она пересекает и
параллельную ей прямую b
в некоторой точке N.
N
Прямая р лежит также в плоскости
, поэтому N – точка
плоскости . Значит, N – общая точка прямой b и
плоскости
.

18.

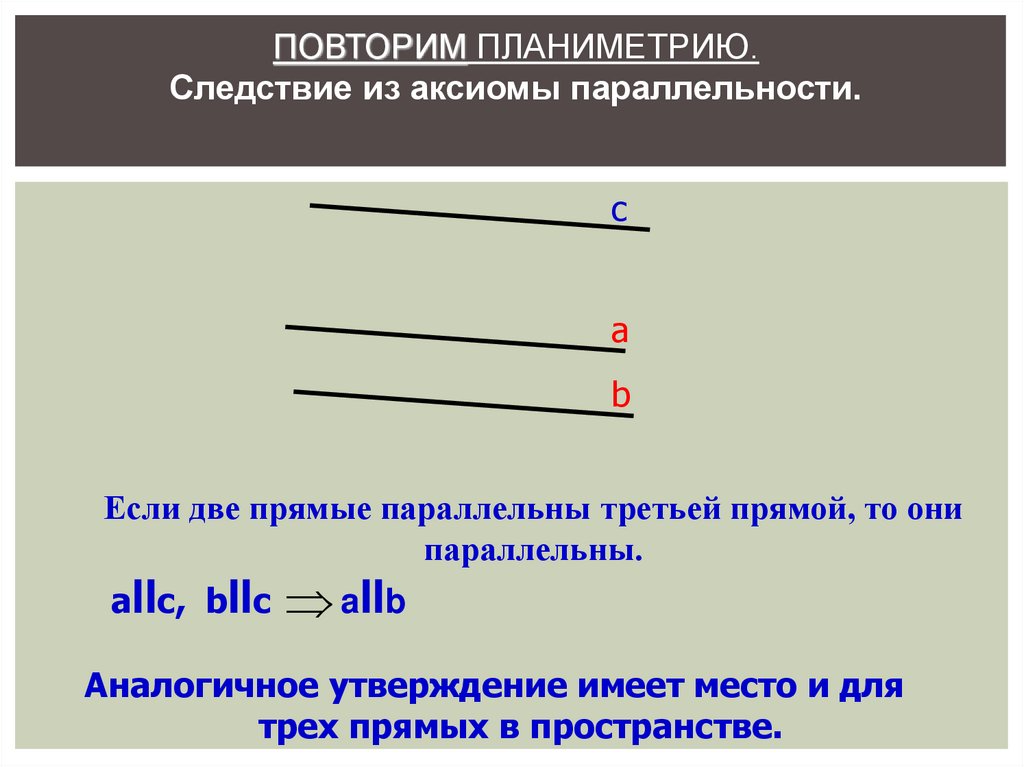
ПОВТОРИМ ПЛАНИМЕТРИЮ.
Следствие из аксиомы параллельности.
с
а
b
Если две прямые параллельны третьей прямой, то они
параллельны.
aIIс, bIIс aIIb
Аналогичное утверждение имеет место и для
трех прямых в пространстве.

19.

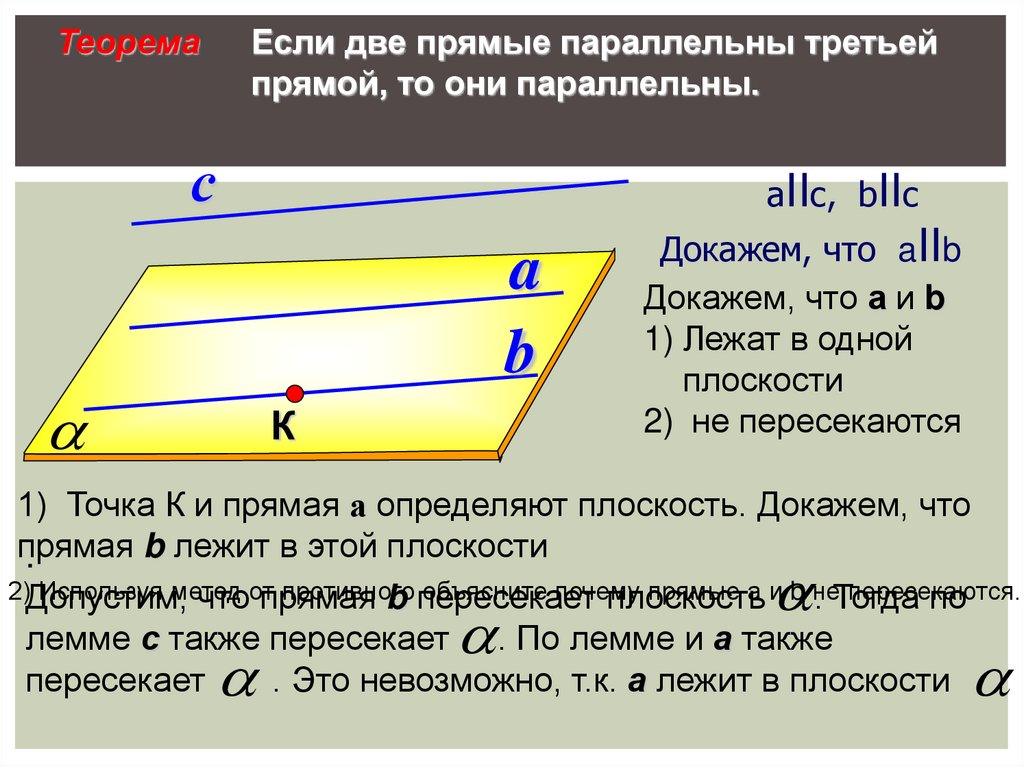
Теорема
Если две прямые параллельны третьей
прямой, то они параллельны.
с
aIIс, bIIс
a
b
К
Докажем, что aIIb
Докажем, что а и b
1) Лежат в одной
плоскости
2) не пересекаются
1) Точка К и прямая а определяют плоскость. Докажем, что
прямая
b лежит в этой плоскости
.
2)Допустим,
Используя метод
противного
объясните почему
прямые а и b не
пересекаются.
чтоотпрямая
b пересекает
плоскость
. Тогда
по
лемме с также пересекает . По лемме и а также
пересекает
. Это невозможно, т.к. а лежит в плоскости

20.

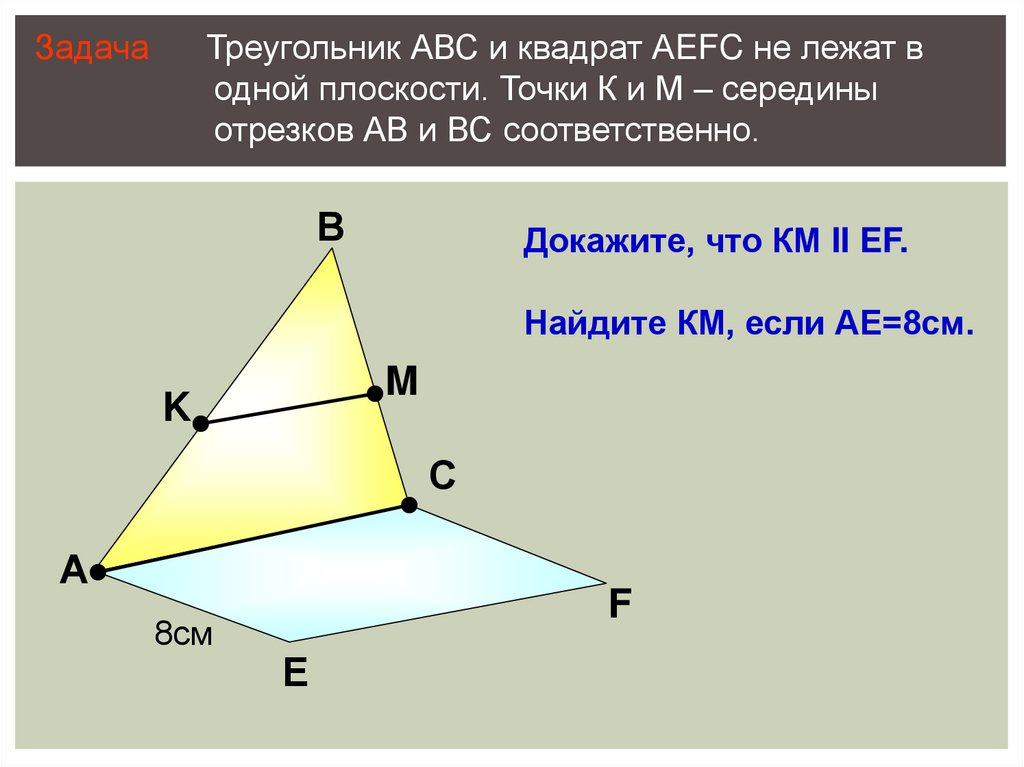
Задача
Треугольник АВС и квадрат АEFC не лежат в
одной плоскости. Точки К и М – середины
отрезков АВ и ВС соответственно.
В
Докажите, что КМ II EF.
Найдите КМ, если АЕ=8см.
M
K
С
А
8см
F
Е

21.

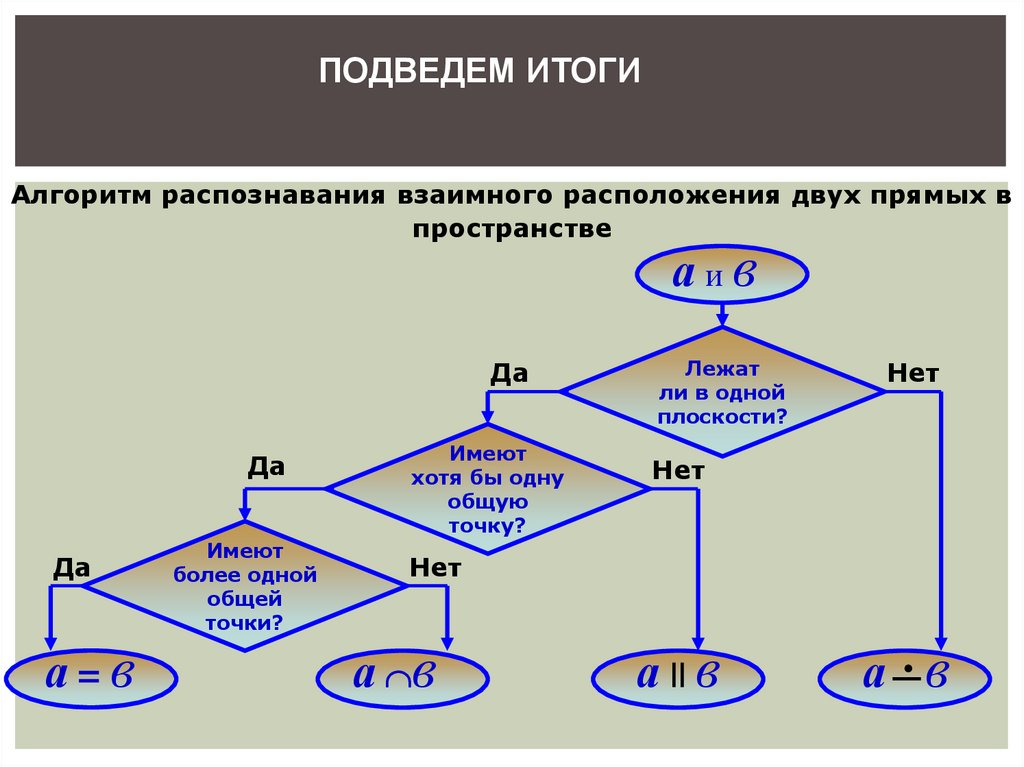
ПОДВЕДЕМ ИТОГИ
Алгоритм распознавания взаимного расположения двух прямых в
пространстве
аив
Да
Да
Да
а=в
Имеют
более одной
общей
точки?
Имеют
хотя бы одну
общую
точку?
Лежат
ли в одной
плоскости?
Нет
Нет
Нет
а в
а
в
а .в

22.

Найдите на рисунке параллельные прямые.
Назовите параллельные прямые и плоскости.
Найдите скрещивающиеся прямые.

23.

ДОМАШНЕЕ ЗАДАНИЕ
П. 4, 5 теоремы
Понятия: параллельность отрезков, отрезка и
прямой, двух лучей в пространстве
Задачи №16, 18

24.

Используемая литерат ура:
1 . Атанасян Л.С. Геометрия, 10-11[Текст]: учебник для
общеобразовательных учреждений/ Атанасян Л.С., В.Ф.
Бу т узов, С.Б. Кадомцев и др. –13-е изд. - М.: Просвещение,
2013.-206 с.: ил.-ISBN5-09-013293-3.
2. Яровенко В.Я.Поурочные разработки по геометрии:10
класс [Текст] – М.: ВАКО,2010.-304 с.- (В помощь школьному
учителю). ISBN978-5-408-00166-8.