Решение задач на вычисление рекуррентных выражений. Задание 16

1.

Решение задач на вычисление
рекуррентных выражений.
Подходы к решению заданий № 16 ЕГЭ-2021
Леонова Елена Валентиновна,
учитель информатики ГБОУ Школа № 1238

2.

КЕГЭ 16
Проверяемый результат обучения:
Умение вычисления рекуррентных выражений
Уровень сложности – повышенный.
Максимальный балл – 1 балл.
Примерное время выполнения задания – 9 мин.
Использование специализированного ПО – да.
Используемое ПО:
• среды программирования;
• электронные таблицы.
2

3.

Сегодня мы рассмотрим подходы к решению следующих
видов задач ЕГЭ 16
Определите значение:
рекурсивного вызова F(n) для больших значений n;
количества напечатанных символов «*»;
символьной строки, полученной после работы рекурсивной функции;
наименьшего (наибольшего) n, при котором F(n) будут больше (меньше, равны)
значению некоторого X.
3

4.

Пример 1
Пример 1 (демо-2021). Алгоритм вычисления функции F(n) задан следующими
соотношениями:
F(n) = 1 при n = 1
F(n) = n + F(n–1), если n чётно,
F(n) = 2· F(n–2), если n > 1 и n нечётно.
Чему равно значение функции F(26)?
Решение (способ 1). Составим рекурсивную функцию.
Запустив функцию для значения F(26), мы получаем
ответ 4122.
Как убедиться, что мы получили верный ответ?
Для этого необходимо вычислить аналитически
небольшие значения, например F(5) и F(6), и сравнить
полученные результаты с выводом функции или
решением с помощью электронных таблиц.
4

5.

Пример 1 (демо-2021)
Проверка правильности работы рекурсивной функции
осуществляется на двух тестах, ответы на которые несложно
вычислить аналитически.
F(5)=2*F(3)=2*2=4
F(3)=2*F(1)=2*1=2
F(6)=6+F(5)=6+F(5)=6+4=10
5

6.

Пример 1 (демо-2021)
Решение (способ 2). Решение с помощью электронных таблиц.
1) Для этого способа решения необходимо знать, как записывается в электронных
таблицах функция нахождения остатка (для проверки чётности) и функция выбора.
2) Зададим значение F(1)=1 и F(2)=3.
Cо значения F(3) мы можем воспользоваться формулой, так как
для него уже есть вычисленные F(1) в ячейке В2 и F(2)
в ячейке В3.
3) Проверим значения F для простых
значений F(5) и F(6), вычисленных
аналитически. Если они верны, то,
скопировав формулу до значения F(26), мы
получим ответ 4122.
6

7.

Пример 2
Пример 2. Определите, сколько символов * выведет эта процедура при вызове F(20).
def F( n ):
print('*')
if n >= 1:
print('*')
F(n-1)
F(n-2)
F(n-3)
Решение (способ 1):
1) Построим рекурсивную функцию f(n), которая определит количество выведенных звёздочек.
2) Основная часть определения рекурсивной функции – рекуррентная формула для остальных
случаев. При n 1 процедура печатает одну звёздочку сразу при входе в процедуру, затем –
ещё одну в теле условного оператора, а затем трижды вызывает сама себя с разными
значениями параметра.
при n 1
f(n) = 1 + 1 + f(n–1) + f(n–2) + f(n–3)
при n<1
f(n)=1
3) Теперь эту функцию можно записать в виде программного кода.
4) Мы получили ответ.
Как убедиться, что он верный?
7

8.

Пример 2
Пример 2. Определите, сколько символов * выведет эта процедура при вызове F(20).
def F( n ):
print('*')
if n >= 1:
print('*')
F(n-1)
F(n-2)
F(n-3)
Решение (способ 1):
5) По рекуррентному соотношению
при n 1
при n<1
f(n) = 1 + 1 + f(n–1) + f(n–2) + f(n–3)
f(n)=1
вычислим аналитически значение вызова f(4).
f(4)=2+f(3)+f(2)+f(1)=
2+17+9+5=33
f(3)=2+f(2)+f(1)+f(0)=
2+9+5+1=17
f(2)=2+f(1)+f(0)+f(-1)=
2+5+1+1=9
f(1)=2+f(0)+f(-1)+f(-2)= 2+1+1+1=5
(жирным выделены значения функции, которые
не требуют новых рекурсивных вызовов)
6) Запустим функцию для значения f(5), предварительно вычисленного аналитически.
Сравним полученные значения. Если они верны, то и f(20) верно.
8

9.

Пример 2
Решение (способ 2) Решим задание
с использованием электронных таблиц.
при n 1
при n<1
1) По рекуррентной формуле видно, что диапазон
n лучше начать с нескольких отрицательных
значений, чтобы одной формулой можно было
задать все значения, опираясь на известные.
f(n) = 1 + 1 + f(n–1) + f(n–2) + f(n–3)
f(n)=1
2) Проверим, как ведёт себя полученная в таблице
формула на значении f(5), предварительно
вычисленном аналитически.
3) Убедившись, что значения совпали, скопируем формулу
до значения f(20) и увидим конечный результат.
9

10.

Задачи для тренировки № 1
(№ 22) Определите, сколько символов *
выведет эта процедура при вызове F(35):
def F( n ):
print('*')
if n >= 1:
print('*')
F(n-1)
F(n-2)
print('*')
(№ 21) Определите, сколько символов *
выведет эта процедура при вызове F(28):
def F( n ):
print('*')
if n >= 1:
print('*')
F(n-1)
F(n-2)
В презентации использованы задачи Демоверсии ЕГЭ-2021
и задачи №16 ЕГЭ (с сохранением нумерации) с сайта К.Ю. Полякова http://kpolyakov.spb.ru/school/ege.htm
10

11.

Пример 3
Пример 3 (№ 26 П) Определите наименьшее значение n, при котором сумма чисел, которые будут
выведены при вызове F(n), будет больше 1000000. Запишите в ответе сначала найденное значение n,
а затем через пробел – соответствующую сумму выведенных чисел.
def F( n ):
print(n+1)
if n > 1:
print(n+5)
F(n-1)
F(n-2)
Решение (способ 1).
1) Составим рекуррентное выражение.
При n>1
F(n)=(n+1)+(n+5)+F(n-1)+F(n-2), упростим F(n)=2*n+6+F(n-1)+F(n-2)
При n<=1 F(n)= n+1
2) Запишем реализующую это выражение рекурсивную функцию.
3) Для проверки работы функции запустим её для F(2), вычислим F(2) аналитически и сравним значения.
F(2)=2*2+6+F(1)+F(0)=4+6+2+1=13
F(1)=1+1=2
F(0)=0+1=1
11

12.

Пример 3
4) Теперь в основной программе реализуем алгоритм поиска наименьшего значения функции,
последовательно вычисляемого от целых чисел >=0.
Переменной x даем значение равное 0, так как
в аналитическом решении минимальное значение,
которое нам понадобилось, было F(0).
F(2)=2*2+6+F(1)+F(0)=4+6+2+1=13
F(1)=1+1=2
F(0)=0+1=1
5) Можно было бы реализовать алгоритм и без
использования цикла с постусловием, но такая
программа будет работать медленнее, так как
при выводе мы снова запускаем рекурсию.
6) Итак, ответ получен. 24 – наименьшее
значение при котором функция выведет
значение 1114369 большее 1000000.
12

13.

Пример 3
Решение (способ 2).
1) Составим рекуррентное выражение.
При n>1
F(n)=(n+1)+(n+5)+F(n-1)+F(n-2), упростим F(n)=2*n+6+F(n-1)+F(n-2)
При n<=1 F(n)= n+1
2) Реализуем рекуррентные выражения в электронных таблицах.
13

14.

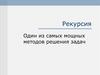
Пример 3
Решение (способ 2) продолжение.
3) Для организации поиска наименьшего значения n, при котором
F(n)>1000000 воспользуемся условным форматированием по
столбцу В.
4) Выделение ячеек после
обработки условным
форматированием позволит найти
искомое наименьшее значение n.
Ответ: 24 1114369
14

15.

Задачи для тренировки № 2
(№ 27) Определите наименьшее значение n, при
котором сумма чисел, которые будут выведены
при вызове F(n), будет больше 1000000. Запишите в
ответе сначала найденное значение n, а затем
через пробел – соответствующую сумму
выведенных чисел.
def F( n ):
print(n+1)
if n > 1:
print(2*n)
F(n-1)
F(n-3)
(№ 30) Определите наименьшее значение n, при
котором сумма чисел, которые будут выведены
при вызове F(n), будет больше 3200000. Запишите
в ответе сначала найденное значение n, а затем
через пробел – соответствующую сумму
выведенных чисел.
def F( n ):
print(n*n)
if n > 1:
print(2*n+1)
F(n-2)
F(n//3)
15

16.

Пример 4
Пример 4 (№ 31) (Д. Ф. Муфаззалов) Определите наименьшее значение n, при котором значение F(n) будет
больше числа 320. Запишите в ответе сначала найденное значение n, а затем через пробел –
соответствующее значение F(n).
def F(n):
if n>0:
return n%10*F(n//10)
else: return 1
3) Составим рекурсивную функцию.
Решение (способ 1).
1) Нам нужно найти наименьшее значение
n, при котором последнее выведенное
значение F(n) станет больше 320.
2) Составим рекуррентное выражение для
нахождения выводимого значения.
При n<=0
F(n)=1
При n>0
F(n)=(n%10)+F(n//10)
4) В основной программе реализуем алгоритм
поиска наименьшего значения. Получим ответ.
16

17.

Пример 5
Пример 5 № 33 (Д. Ф. Муфаззалов) Определите наименьшее значение n, такое, что последнее выведенное число
при вызове F(n) будет больше числа 32. Запишите в ответе сначала найденное значение n, а затем через пробел –
соответствующее значение F(n).
Решение.
def F(n):
print(n)
if n>0:
d=n%10+F(n//10)
print(d)
return d
else: return 0
Составим рекуррентное соотношение, описывающее что будет
выводить (печатать) функция F(n)
При n>0 F(n) печатает n%10+F(n//10)
При остальных n печатает n.
1)
2) Составим рекурсивную функцию.
3) В основной программе реализуем алгоритм поиска вызова
со значением >32.
Ответ:
17

18.

Пример 6
Пример 6 (ЕГЭ 2020) Ниже на пяти языках программирования записан рекурсивный алгоритм F. Запишите
подряд без пробелов и разделителей все числа, которые будут показаны на экране при выполнении вызова F(9).
Числа должны быть записаны в том же порядке, в котором они выводятся на экран.
def F(n):
if n > 3:
F(n // 2)
F(n - 2)
print(n, end='')
Способ 1 (решение с помощью
рекурсивной процедуры)
Решение.
Этот пример задания прошлых лет позволит нам вспомнить, как можно
реализовать строковый вывод в рекурсивных процедурах и функциях.
Способ 2 (решение с помощью
рекурсивной функции)
Составим рекурсивную
функцию, которая в строковой
переменной s будет собирать
результаты вызовов F(n//2) и
F(n-2) и закончит работу при
n<=3.
18

19.

Пример 7
Пример 7. Определите количество различных натуральных
значений n, таких, что значение F(n,2) находится в диапазоне
[100, 1000].
F(n,m) определяется соотношениями
при m=0 F(n,m)=1
при m>0 F(n,m)=n*F(n,m-1)
Решение:
1) По рекуррентному соотношению составим рекурсивную
функцию.
2) В основной программе для решения задачи нужно
составить программу поиска значений функции
в диапазоне [100, 1000].
Значение второго аргумента функции по условию не
меняется. Оно всегда равно 2. Поэтому циклическим
перебором организуем нарастание первого аргумента.
Ответ:
19

20.

Пример 8
Пример 8. Определите количество различных значений n, таких, что n и m натуральные числа,
а значение F(n,m) равно числу 30.
F(n,m)=0, при m=0
F(n,m)=n+F(n,m-1), при m <>0
Решение.
1) По рекуррентному выражению
составим рекурсивную функцию.
2) Составим трассировочную таблицу для нескольких
первых значений функции.
Из таблицы видно, что F(n,m)=n*m
Теперь решение сводится к поиску таких пар n, m при
которых их произведение равно 30.
Нетрудно понять, что это могут быть лишь пары,
составленные из чисел 1 и 30, 2 и 15, 3 и 10, 5 и 6.
m
F(n, m)
0
0
1
n+0
2
n+F(n,1)=n+n+0=2*n
3
n+F(n,2)=n+2*n=3*n
…
20

21.

Пример 8
Пример 8. Определите количество различных значений n, таких, что n и m натуральные числа,
а значение F(n,m) равно числу 30.
F(n,m)=0, при m=0
F(n,m)=n+F(n,m-1), при m <>0
Решение (продолжение).
3) В основной программе реализуем перебор всех пар n и m.
Так как F(n,m)=n*m, то чтобы получить 30, n и m должны меняться от 0 до 30.
4) В основной программе можно организовать не только подсчет, но и
вывод найденных значений F(n,m).
Ответ: 8
21