Aplicația MATLAB. Fișiere și algoritme

1.

Aplicația MATLAB. Fișiere și
algoritme.
lect.univ. ing. CUTIA Evgheni
Departamentul Inginerie Civilă și Geodezie
Facultatea Construcții, Geodezie și Cadastru
Universitatea Tehnică a Moldovei
[email protected]
1

2.

Funcții și algoritme
Fișiere tip script.
Fișiere tip function.
Algoritme. Metoda schemelor logice.
Algoritme. Metoda pseudocod.
Tipuri de structuri.
2

3.

Fișiere
script
Fişierele care conţin cod
MATLAB sunt numite Mfiles sau fişiere .m. Aceste
fişiere
pot
fi
funcţii
(functions)
care
acceptă
argumente de intrare şi
furnizează ieşiri, sau pot fi
fişiere script care execută o
serie
de
instrucţiuni
MATLAB.
Pentru
ca
MATLAB-ul să recunoască
un fişier ca fişier M-file
trebuie ca numele acestuia să
se termine cu extensia .m.
Nu acceptă
argumente de
intrare și nu
returnează ieșiri
Fișiere
function
Acceptă
argumente de
intrare și
returnează ieșiri
Operează cu
datele din
workspace
Variabilele
interne ale
funcției sunt
locale(implicit)
Utile pentru
automatizarea
unei serii de pași
care trebuie
executați de
multe ori
Utile pentru
exinderea
limbajului
MATLAB
pentru diverse
aplicații
3

4.

Fişierele script sunt cele mai simple fişiere MATLAB, nu au argumente de
intrare sau de ieşire şi sunt utile pentru executarea secvenţială a unor calcule care
altfel ar trebui executate în mod repetat de la linia de comandă. Script-urile
operează cu datele din workspace sau pot crea date noi. Aceste date sunt
disponibile după terminarea execuţiei fişierului.
În structura fişierului script se observă existenţa celulelor de calcul, a
datelor iniţiale şi a instrucţiunilor de calcul, fără însă a se utiliza funcţii definite de
utilizator.
4

5.

Funcțiile sunt programe care rezolvă anumite cerințe (de exemplu calculul
mediei elementelor dintr-o matrice, transformarea unei imagini color într-o imagine
grayscale, redarea unui semnal audio, antrenarea unei rețele neurale etc). Atunci
când avem de dezvoltat o aplicație mai complexă este bine ca aceasta să fie împărțită
în module mai mici care să rezolve doar anumite cerințe, fiecare modul fiind
implementat într-o funcție.
Această abordare modulară face ca un program să fie ușor de urmărit și de
un alt utilizator și permite un debug mai eficient. O aplicație care a fost dezvoltată
modular este mult mai ușor de dezvoltat ulterior, prin simpla adăugare a altor
module (funcții). Un alt avantaj al folosirii funcțiilor este reutilizarea, ceea ce
înseamnă că o funcție odată creată poate fi folosită de oricâte ori (evitându-se astfel
multiplicarea redundantă a codului). De asemenea, o funcție creată pentru o aplicație
poate fi apoi refolosită într-o altă aplicație.
5

6.

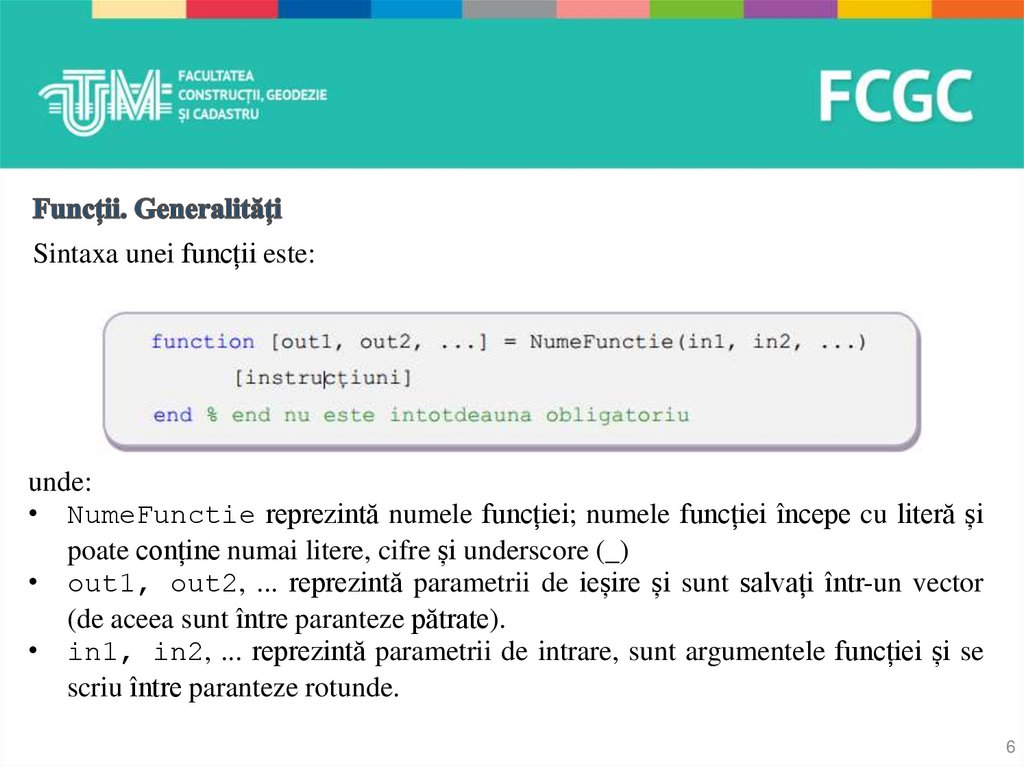
Sintaxa unei funcții este:
unde:
• NumeFunctie reprezintă numele funcției; numele funcției începe cu literă și
poate conține numai litere, cifre și underscore (_)
• out1, out2, ... reprezintă parametrii de ieșire și sunt salvați într-un vector
(de aceea sunt între paranteze pătrate).
• in1, in2, ... reprezintă parametrii de intrare, sunt argumentele funcției și se
scriu între paranteze rotunde.
6

7.

• numele fișierului în care se salvează funcția trebuie să coincidă cu numele
funcției; dacă numele funcției este NumeFunctie atunci numele fișierului trebuie
să fie NumeFunctie.m
• prima linie care se execută din fișierul în care este salvată funcția conține antetul
funcției (înainte de antet pot exista doar comentarii).
• nu este obligatoriu ca o funcție să aibă parametri de intrare și nici parametri de
ieșire.
Este recomandat ca imediat după antetul funcției să existe comentarii sugestive
referitoare la: utilitatea funcției, care este semnificația parametrilor de intrare și a
celor de ieșire, când a fost modificată funcția ultima dată și de către cine etc (aceste
comentarii vor fi afișate atunci când se rulează comanda >> help NumeFunctie).
7

8.

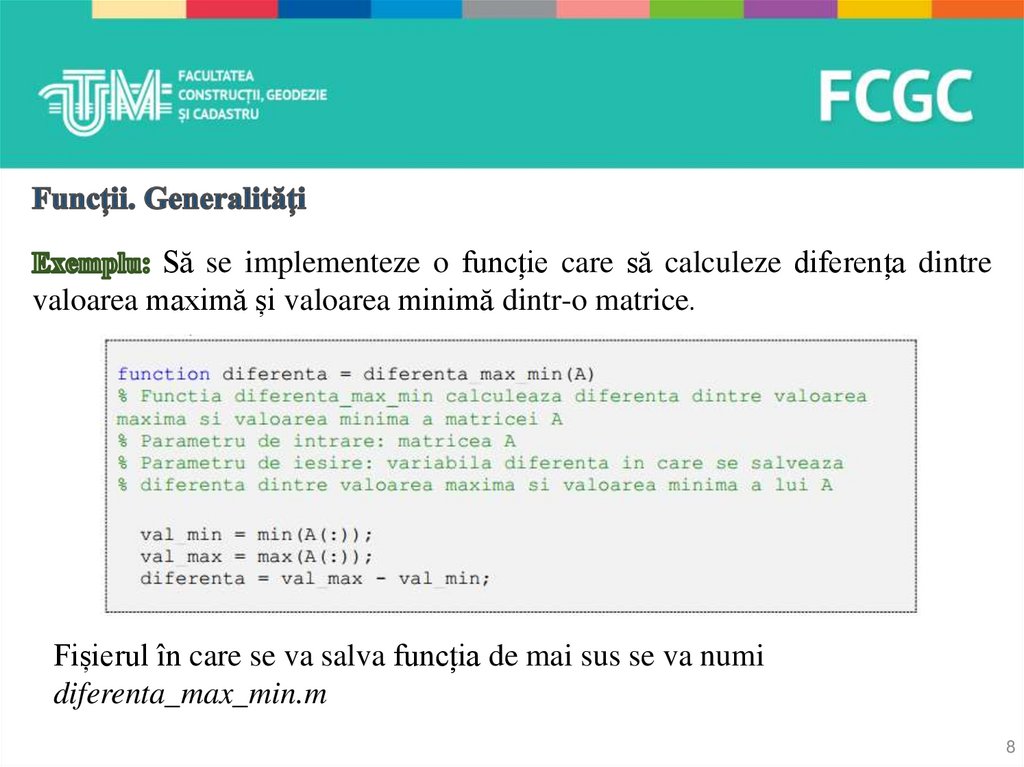
Să se implementeze o funcție care să calculeze diferența dintre
valoarea maximă și valoarea minimă dintr-o matrice.
Fișierul în care se va salva funcția de mai sus se va numi
diferenta_max_min.m
8

9.

Să se afișeze
diferenta_max_min
în
Command
Window
help-ul
funcției
Pentru a putea utiliza o funcție, aceasta se apelează folosind sintaxa:
O funcție se poate apela din Command Window, dintr-un program script sau dintro altă funcție. Pentru ca o funcție să fie găsită atunci când este apelată, aceasta
trebuie să se afle în directorul curent sau într-unul dintre directoarele aflate în căile
de căutare ale MATLAB-ului.
9

10.

Folosind funcția diferenta_max_min creată mai sus, să se
calculeze diferența dintre maximul și minimul unei matrice A.
Un fișier poate conține mai multe funcții: prima funcție numită și funcție principală
urmată de alte funcții numite subfuncții. În acest caz numele fișierului trebuie să
coincidă cu numele funcției principale.
10

11.

Un fișier poate conține mai multe funcții: prima funcție numită și funcție principală
urmată de alte funcții numite subfuncții. În acest caz numele fișierului trebuie să
coincidă cu numele funcției principale.
Dacă într-un fișier există o singură funcție, este opțională terminarea acesteia cu end.
Dacă un fișier conține mai multe funcții, ori se termină toate cu end, ori nu se va
folosi end la sfârșitul niciunei funcții.
11

12.

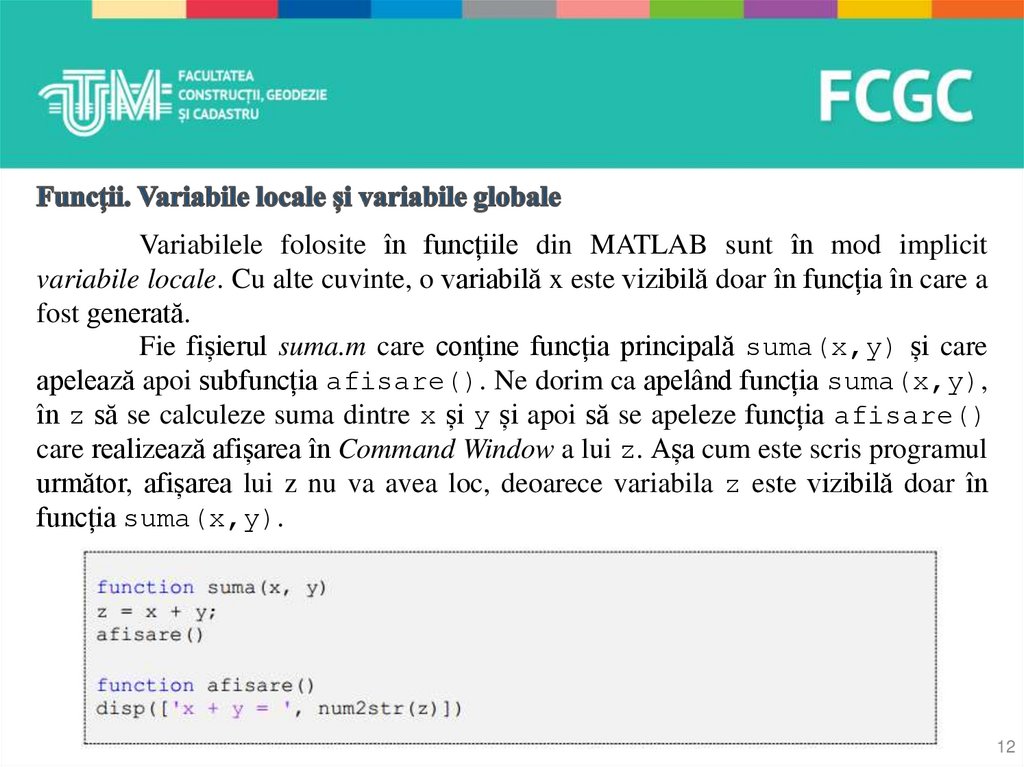
Variabilele folosite în funcțiile din MATLAB sunt în mod implicit
variabile locale. Cu alte cuvinte, o variabilă x este vizibilă doar în funcția în care a
fost generată.
Fie fișierul suma.m care conține funcția principală suma(x,y) și care
apelează apoi subfuncția afisare(). Ne dorim ca apelând funcția suma(x,y),
în z să se calculeze suma dintre x și y și apoi să se apeleze funcția afisare()
care realizează afișarea în Command Window a lui z. Așa cum este scris programul
următor, afișarea lui z nu va avea loc, deoarece variabila z este vizibilă doar în
funcția suma(x,y).
12

13.

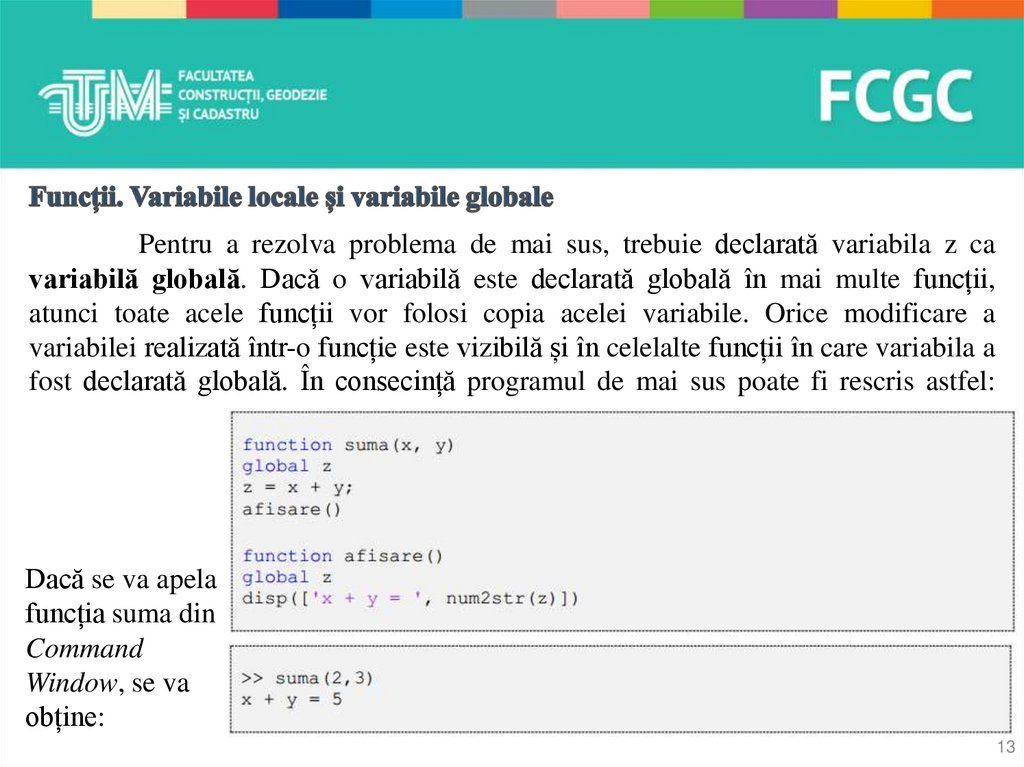
Pentru a rezolva problema de mai sus, trebuie declarată variabila z ca
variabilă globală. Dacă o variabilă este declarată globală în mai multe funcții,
atunci toate acele funcții vor folosi copia acelei variabile. Orice modificare a
variabilei realizată într-o funcție este vizibilă și în celelalte funcții în care variabila a
fost declarată globală. În consecință programul de mai sus poate fi rescris astfel:
Dacă se va apela
funcția suma din
Command
Window, se va
obține:
13

14.

Algoritmul este o metodă de rezolvarea a
unei anumite probleme prin care, pornind de
la datele de intrare şi parcurgând o anumită
succesiune finită de etape, se ajunge în final,
la o serie de date de ieşire care reprezintă
soluţia problemei respective.
Datele de intrare reprezintă toate
informaţiile necesare pentru rezolvarea
problemei respective şi rezultă dintr-o bună
înţelegere a problemei de rezolvat.
Aproximarea şi reducerea numărului datelor
de intrare pot conduce la reducerea
complexităţii algoritmului, dar şi la creşterea
gradului de aproximarea a soluţiei obţinute.
14

15.

Algoritmul este o metodă de rezolvarea a unei
anumite probleme prin care, pornind de la datele de
intrare şi parcurgând o anumită succesiune finită de
etape, se ajunge în final, la o serie de date de ieşire
care reprezintă soluţia problemei respective.
Datele de ieşire reprezintă datele finale
care rezultă în urma aplicării algoritmului de calcul
asupra datelor de intrare. Algoritmul de calcul poate
să furnizeze şi o serie de rezultate intermediare,
care au relevanţă doar în contextul etapelor
intermediare ale algoritmului. Utilizatorul, pe baza
problemei de rezolvat, va decide care din
rezultatele intermediare reprezintă şi datele de ieşire
relevante
pentru
soluţia
problemei.
15

16.

Principale proprietăţi ale algoritmilor sunt:
Determinarea. Algoritmul trebuie să fie astfel conceput încât toate etapele, ca şi
ordinea lor de executare, să fie clare, concise şi fără ambiguităţi.
Generalitatea. Algoritmul trebuie să permită rezolvarea unei familii de probleme
şi nu a unei probleme particulare.
Finitudinea. Algoritmul poate să conţină un număr oricât de mare
de etape, totuşi, numărul etapelor trebuie să fie finit. Principalele obiecte care intră
în structura algoritmilor sunt:
Constantele - reprezintă date (numerice, alfanumerice, logice) care nu se
modifică pe parcursul executării unui algoritm.
Variabilele - reprezintă datele care se modifică pe parcursul executării
unui algoritm.
16

17.

Principale proprietăţi ale algoritmilor sunt:
Operatorii - reprezintă operaţiile care se execută asupra constantelor şi variabilelor
unui algoritm.
Principalele tipuri de operatori sunt:
Operatori aritmetici: adunare +, scădere -, înmulţire *, împărţire /.
Operatori relaţionali: mai mare >, mai mic <, mai mare sau egal >=, mai mic sau
egal <=, egal =, diferit ~=.
Operatori logici: conjuncţie logică AND, disjuncţie logică OR, negaţie logică
NOT.
Expresiile - reprezintă ansamblul constantelor, variabilelor şi al operatorilor dintre
acestea. Expresiile pot fi aritmetice, relaţionale şi logice.
17

18.

Reprezintă un limbaj în care diferitele elemente ale unui algoritm sunt reprezentate
cu ajutorul unor simboluri grafice. Principalele simboluri grafice specifice realizării
schemelor logice sunt prezentate în figura de mai jos.
START
STOP
Bloc de start
Bloc de sfârșit
Blocurile de start (START) şi de
sfârşit (STOP), denumite şi
blocuri de tip terminal, au doar
rolul de a defini punctele
terminale (de început şi de
sfârşit) ale schemei logice. Orice
schemă logică are un bloc de start
şi un bloc de sfârşit.
18

19.

Reprezintă un limbaj în care diferitele elemente ale unui algoritm sunt reprezentate
cu ajutorul unor simboluri grafice. Principalele simboluri grafice specifice realizării
schemelor logice sunt prezentate în figura de mai jos.
INPUT a,b
PRINT u,v
Blocurile de citire (INPUT) şi de scriere
(PRINT) a variabilelor sunt responsabile
cu introducerea datelor de intrare (a, b),
respectiv cu prezentarea datelor de ieşire
(u, v) obţinute după executarea schemei
logice.
19

20.

Reprezintă un limbaj în care diferitele elemente ale unui algoritm sunt reprezentate
cu ajutorul unor simboluri grafice. Principalele simboluri grafice specifice realizării
schemelor logice sunt prezentate în figura de mai jos.
X= ...
Bloc de atribuire
1
Blocul de atribuire permite
definirea unor variabile prin
intermediul expresiilor.
Blocul de conectare permite gruparea
a două intrări într-o singură ieşire, este
identificat printr-un număr şi ajută la
modularizarea schemei logice.
Bloc de conectare
20

21.

Reprezintă un limbaj în care diferitele elemente ale unui algoritm sunt reprezentate
cu ajutorul unor simboluri grafice. Principalele simboluri grafice specifice realizării
schemelor logice sunt prezentate în figura de mai jos.
EL
Bloc condițional
Max(a,b)
Bloc de procedură
Blocul condiţional introduce în schema logică un punct
de ramificare pe baza unei expresii logice. În funcţie de
valoarea de adevăr a acestei expresii logice (adevărat
sau fals), blocul condiţional realizează o ieşire
alternativă, pe una sau cealaltă dintre căile de ieşire ale
blocului.
Blocul de procedură permite compactarea unei
porţiuni a algoritmului într-un singur bloc, asigurând
astfel modularizarea schemelor logice. În interiorul
blocului se specifică numele simbolic al procedurii,
21
variabilele de intrare şi cele de ieşire.

22.

Reprezintă un limbaj în care diferitele elemente ale unui algoritm sunt reprezentate
cu ajutorul unor cuvinte cheie. Cuvintele cheie au în corespondenţă instrucţiuni
specifice în diferite limbaje de programare. Principalele cuvinte cheie (în limba
română) ale metodei de tip pseudocod sunt :
Comenzi de start și de sfârșit
Start
Stop
Comenzi de citire și de scriere a
variabilelor
citește a,b
scrie u,v
Comanda de atribuire
x=expresie
Structura cât timp
cât timp expresie logică execută
Instrucțiune 1
Instrucțiune 2
sfârțit cât timp
Structura repetă până când
repetă
Instrucțiune 1
Instrucțiune 2
până când expresie logică
22

23.

Reprezintă un limbaj în care diferitele elemente ale unui algoritm sunt reprezentate cu
ajutorul unor cuvinte cheie. Cuvintele cheie au în corespondenţă instrucţiuni specifice
în diferite limbaje de programare. Principalele cuvinte cheie (în limba română) ale
metodei de tip pseudocod sunt :
pentru variabilă=valoarea
Dacă expresie logică
Dacă expresie logică
inițială, valoarea finală
atunci
atunci
execută
Instrucțiune 1
Instrucțiune 1
altfel
Instrucțiune 1
Instrucțiune 2
Instrucțiune 2
sfârșit dacă
sfârșit dacă
sfârșit pentru
Structura condițională tip 1
Structura condițională tip 2
Structura pentru
23

24.

• Cuvintele cheie start şi stop corespund începutului şi sfârşitului algoritmului.
Aceste două cuvinte cheie sunt echivalente blocurilor de start (START) şi de
sfârşit (STOP), adică unor simboluri grafice specifice reprezentării algoritmilor
prin metoda schemelor logice.
• Pentru marea majoritate a simbolurilor grafice specifice metodei de reprezentare
a algoritmilor prin metoda schemelor logice există cuvinte cheie echivalente în
metoda pseudocod.
• Comanda de atribuire nu conţine nici un cuvânt cheie. Această comandă este
echivalentă cu blocul de atribuire din metoda schemelor logice.
• Cuvintele cheie citeşte şi scrie corespund comenzilor de introducere a datelor
de intrare (a, b), respectiv de prezentare a datelor de ieşire (u, v) şi sunt
echivalente blocurilor INPUT, respectiv PRINT din metoda schemelor logice.
24

25.

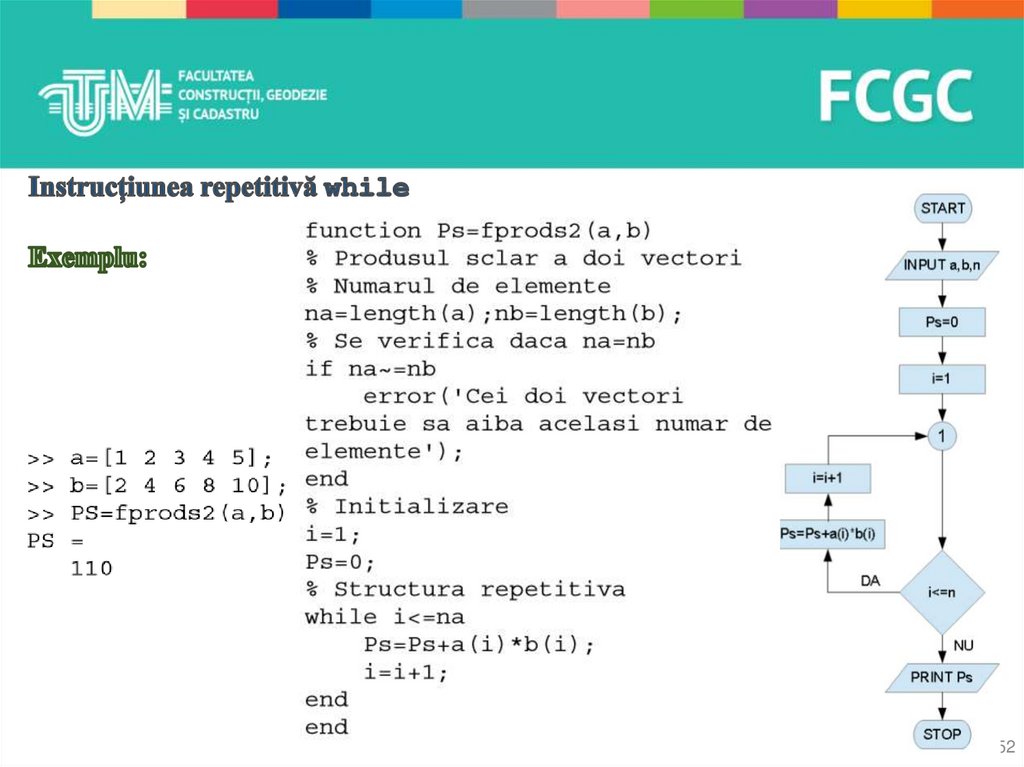
Structura cât timp corespunde unui ciclu repetitiv cu test iniţial.
Structura repetă până când corespunde unui ciclu repetitiv cu test final.
Structura pentru corespunde unui ciclu repetitiv cu număr cunoscut de paşi.
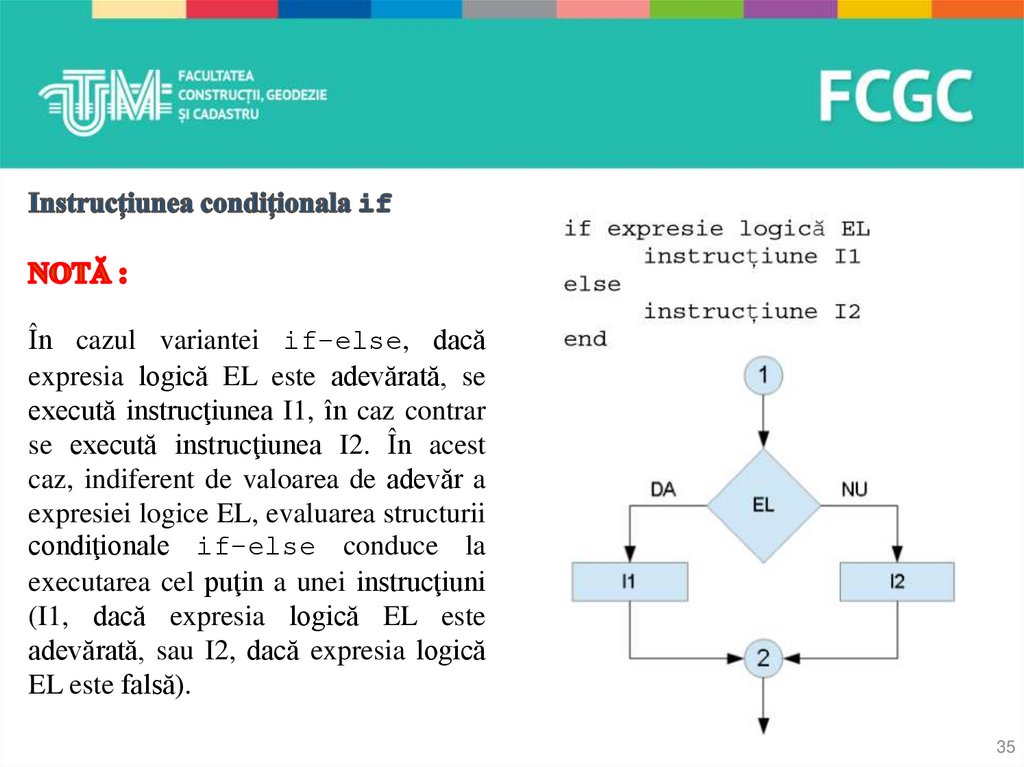
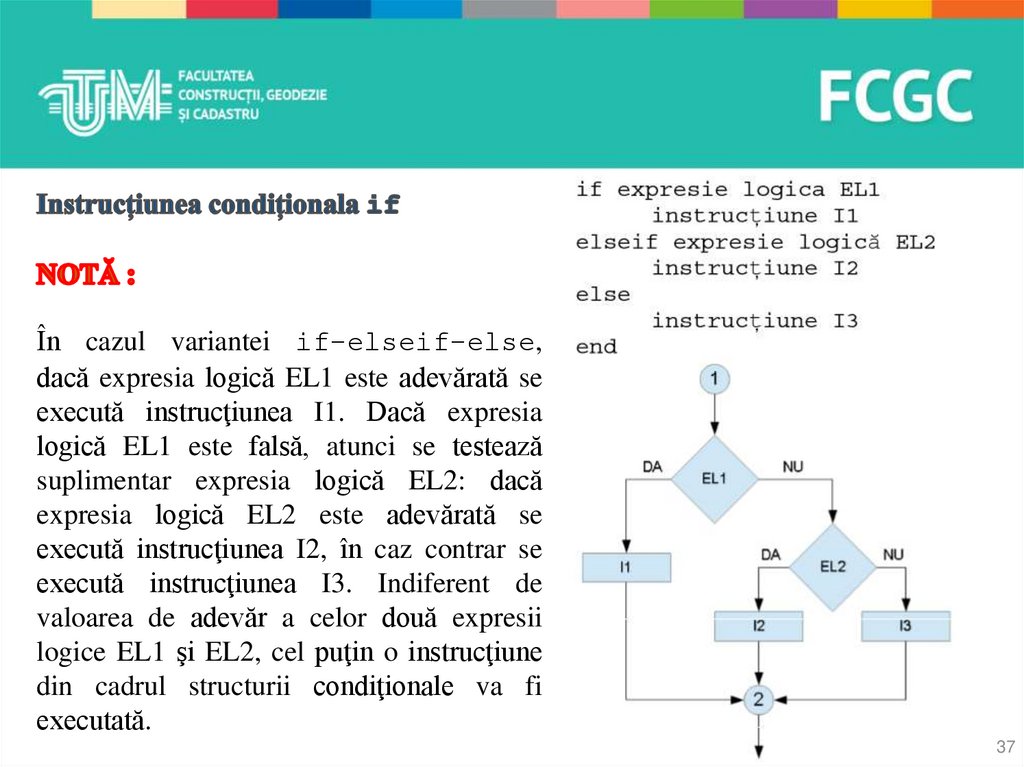
În cazul structurii condiţionale 1, instrucţiunea 1 se execută doar în cazul în
care expresia logică este adevărată. În caz contrar, se va executa instrucţiunea
2. În cazul structurii condiţionale 2, cele două instrucţiuni 1 şi 2 se vor
executa doar dacă este îndeplinită expresia logică, în caz contrar, structura
dacă nu se ia în considerare.
• Structurile condiţionale din metoda pseudocod pot fi transpuse în metoda
schemelor logice pornind de la unul sau mai multe blocuri condiţionale.
25

26.

Teorema programării structurate (Böhm-Jacopini). Orice algoritm cu un
singur punct de început şi un singur punct de sfârşit poate fi descris cu ajutorul
doar a trei tipuri de structuri de control
Structura secvenţială.
Instrucţiunile se execută una după alta,
exact în ordinea în care apar în program.
Schema logică a unei structuri secvenţiale,
de exemplu, cu doar două instrucţiuni I1 şi
I2, este prezentată în figura alăturată
26

27.

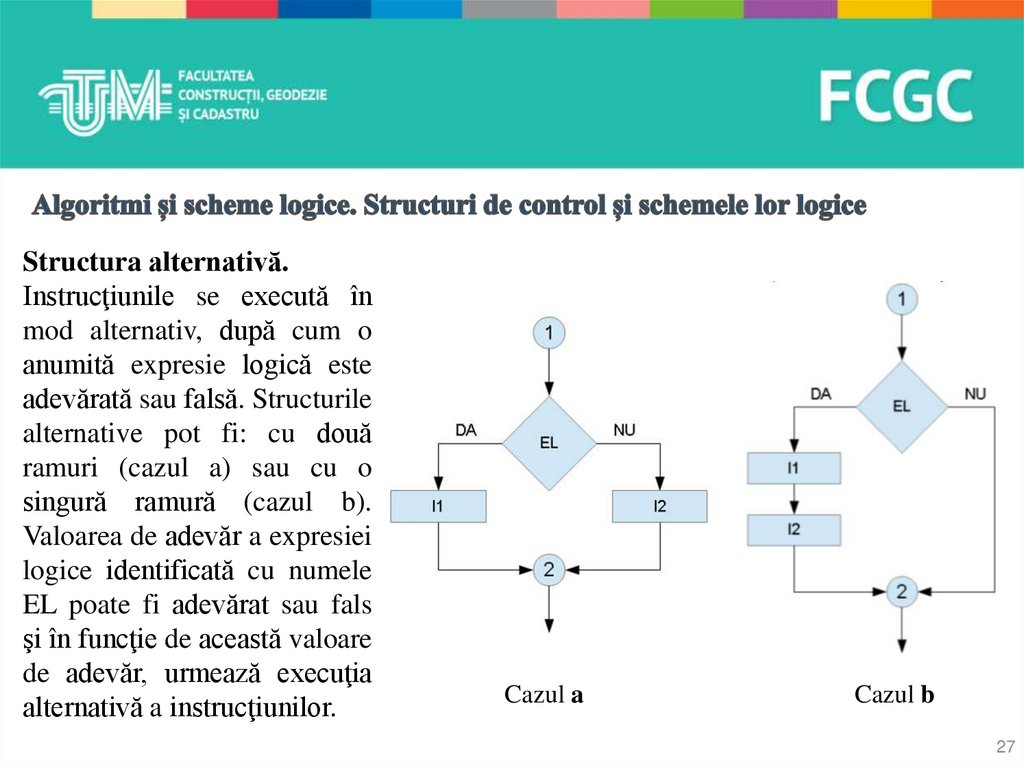
Structura alternativă.
Instrucţiunile se execută în
mod alternativ, după cum o
anumită expresie logică este
adevărată sau falsă. Structurile
alternative pot fi: cu două
ramuri (cazul a) sau cu o
singură ramură (cazul b).
Valoarea de adevăr a expresiei
logice identificată cu numele
EL poate fi adevărat sau fals
şi în funcţie de această valoare
de adevăr, urmează execuţia
alternativă a instrucţiunilor.
Cazul a
Cazul b
27

28.

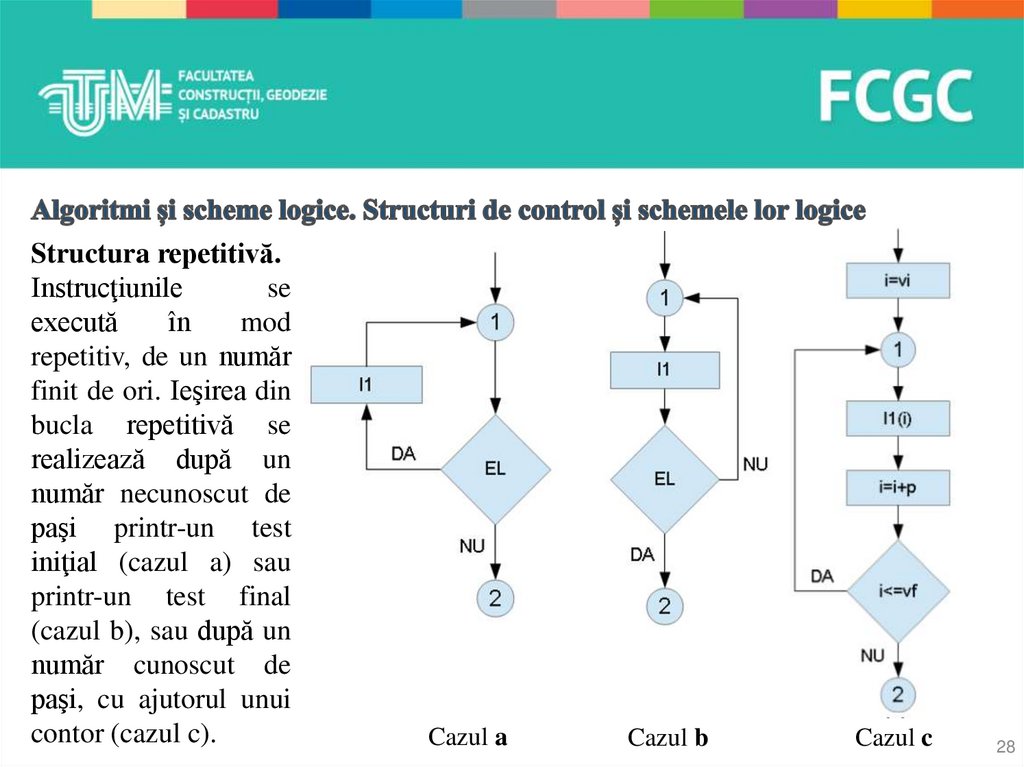
Structura repetitivă.
Instrucţiunile
se
execută
în
mod
repetitiv, de un număr
finit de ori. Ieşirea din
bucla repetitivă se
realizează după un
număr necunoscut de
paşi printr-un test
iniţial (cazul a) sau
printr-un test final
(cazul b), sau după un
număr cunoscut de
paşi, cu ajutorul unui
contor (cazul c).
Cazul a
Cazul b
Cazul c
28

29.

• În cazul structurii repetitive cu test final , instrucţiunea I1 se va executa cel puţin o
singură dacă, deoarece abia după executarea instrucţiuni I1 urmează evaluarea
expresiei logice EL. Dacă expresia logică EL este adevărată se părăseşte structura
repetitivă, în caz contrar se va repeta executarea instrucţiunii I1, după care
urmează din nou evaluarea expresiei logice EL.
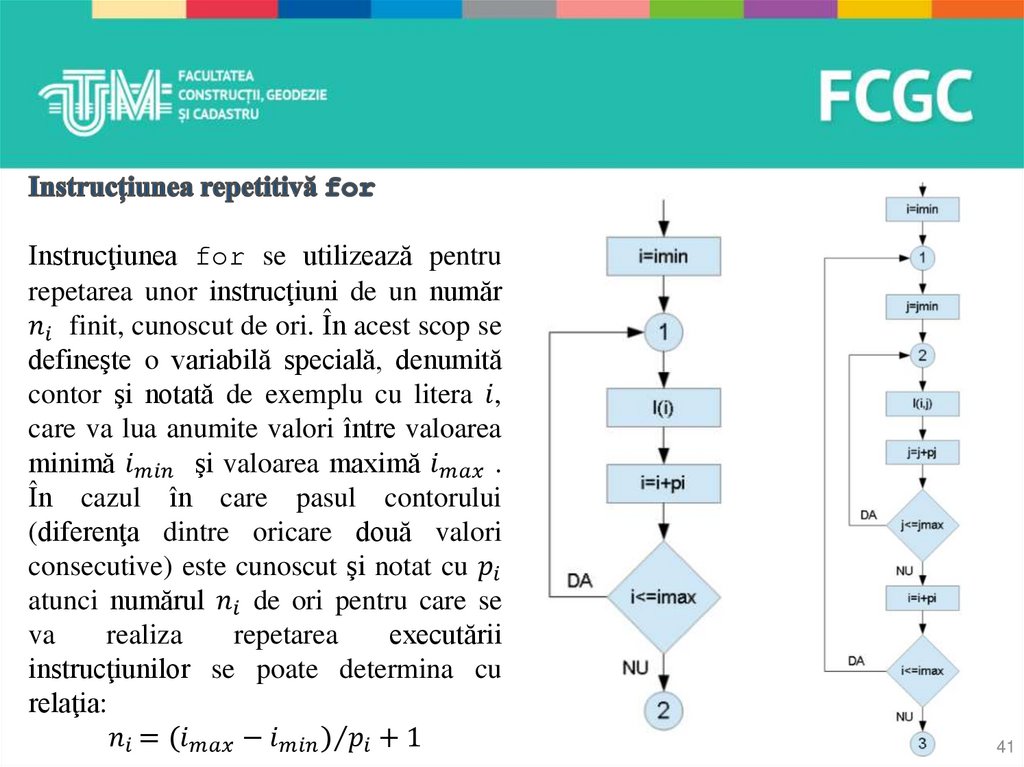
• În cazul structurii repetitive cu contor, se defineşte un contor notat de exemplu cu