Дұрыс көпжақтар

1.

Дұрыс көпжақтар

2.

ТОПТЫҚ ЖҰМЫС
1 топ:
Дұрыс көпжақтардың түрлерін
көрсету және атаулары нені
білдіретінің анықтау
2 топ.
Эйлер теоремасын қолданып
кестені толтыру
3 топ.
Берілген фигураларды қолданып
дұрыс көпжақтың макетін жасау

3.

Дөңес көпжақтың жақтары
қабырғаларының саны бірдей
дұрыс көпжақтар болса және
көпжақтың әрбір төбесінен
шығатын қырларының саны
бірдей болса,онда оны дұрыс
көпжақ деп атайды.

4.

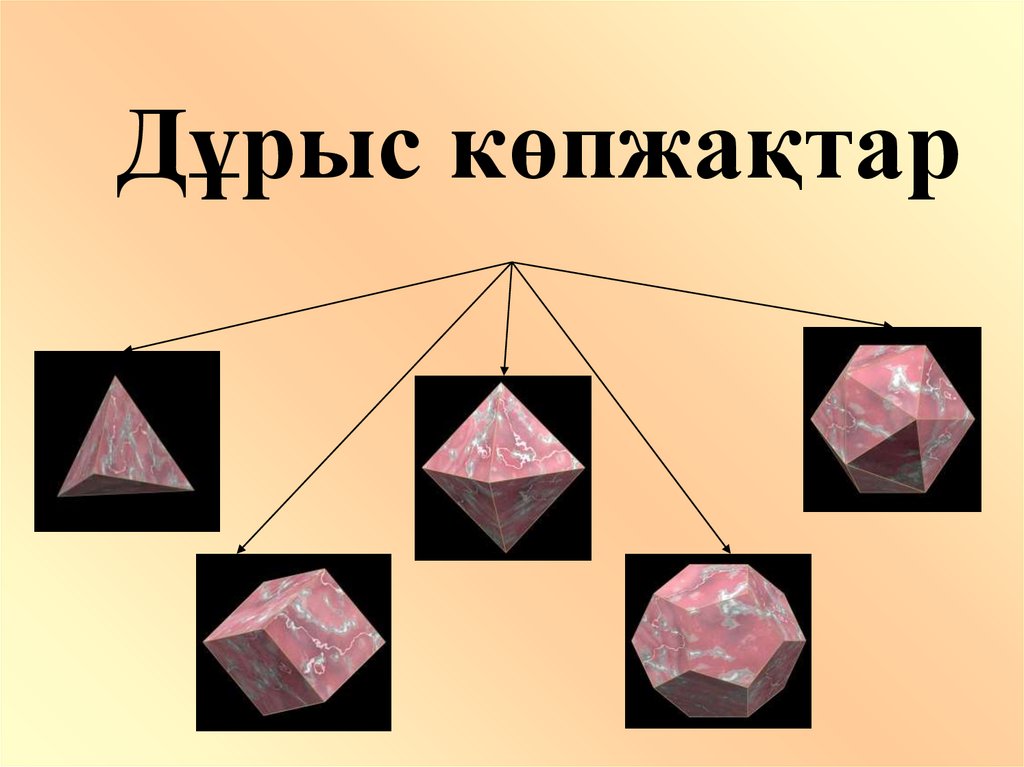
Жақтары дұрыс үшбұрыш болатын
дұрыс көпжақтың 3 түрі болады.
Тетраэдр
Октаэдр
Икосаэдр

5.

Жақтары квадрат
болатын дұрыс
көпбұрыштың 1 түрі
болады.
Жақтары дұрыс
бесбұрыш
болатын дұрыс
көпбұрыштың 1
түрі болады.
Гексаэдр (куб)
Додекаэдр

6.

Платон денелері
Гексаэдр Тетраэдр Октаэдр Икосаэдр Додекаэдр

7.

ДҰРЫС КӨПЖАҚТАРДЫҢ
атаулары жақтарының санына байланысты.
Грек тілінен аударғанда:
«эдра» -жақ
«тетра» - 4
«гекса» - 6
«окта» - 8
«икоса» - 20
«додека» - 12

8.

Леонард Эйлер
(1707 – 1783 жж.)
қ
2
ж+т

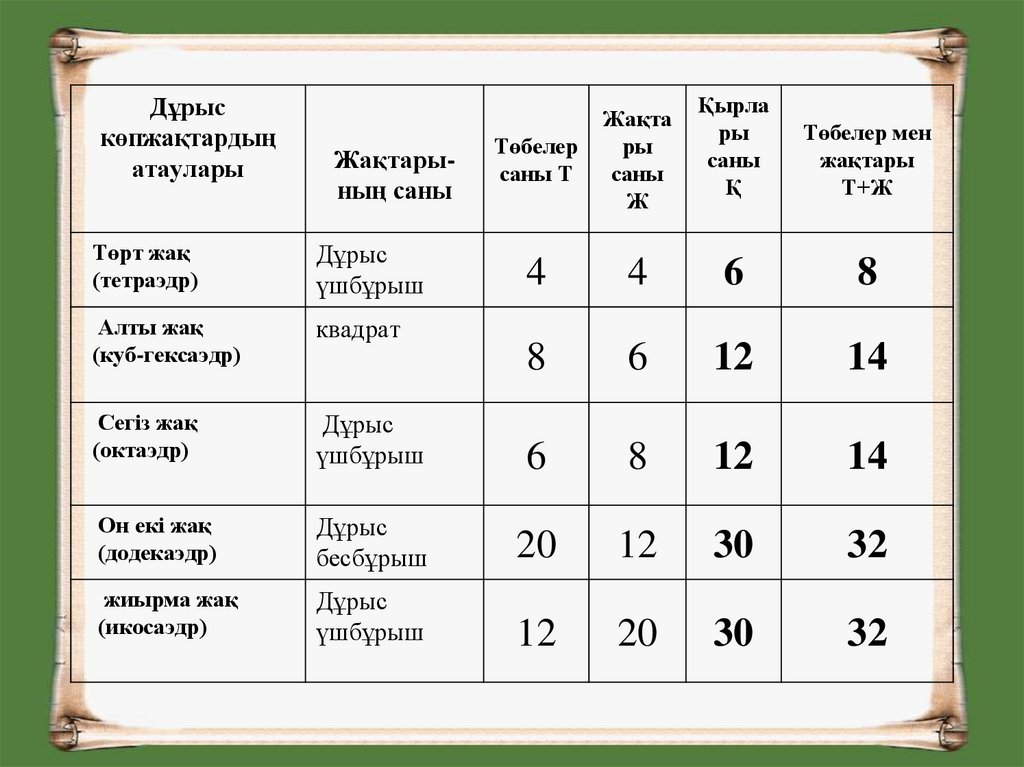
9.

Дұрыс
көпжақтардың
атаулары
Жақтарының саны
Қырла
ры
саны
Қ
Төбелер мен
жақтары
Т+Ж
Төбелер
саны Т
Жақта
ры
саны
Ж
4
4
6
8
8
6
12
14
Төрт жақ
(тетраэдр)
Дұрыс
үшбұрыш
Алты жақ
(куб-гексаэдр)
квадрат
Сегіз жақ
(октаэдр)
Дұрыс
үшбұрыш
6
8
12
14
Он екі жақ
(додекаэдр)
Дұрыс
бесбұрыш
20
12
30
32
жиырма жақ
(икосаэдр)
Дұрыс
үшбұрыш
12
20
30
32

10.

Кестені үлгі бойынша толтырыңдар
α
жақтары
Дұрыс n –
бұрыштың
ішкі
бұрышы.
Дұрыс
үшбұрыш
α = 60º
Квадрат
α = 90º
Дұрыс
бесбұрыш
α = 108º
Дұрыс
алтыбұрыш
α =120º
α·n < 360º
қорытынды
n=3
60°·3 =
180°
180° < 360°
+
n=4 n=5 n=6

11.

12.

13.

ЖАУАПТАРЫ:
1)Д
2)В
3)С
4)А
5)В
6)Д
7)С
8)В
9)С
10)Д

14.

Үйге тапсырма:
Икосаэдр макеті мен
жазбасын жасап келу