Похожие презентации:
Линейные операторы. Тема 14
1.
§14. Линейные операторып.1. Основные определения.
Оператором называется закон, по которому
каждому вектору x пространства R n ставится
в соответствие единственный вектор y
m
пространства R .
Обозначается:
n
m
y A ( x ), A : R R .
Вектор y называется образом вектора x.
Вектор x называется прообразом вектора y.
2.
Пример.A : ( x1 , x 2 ) ( x , x , x x ),
2
1
2
2
2
1
(2, 1) (4,1, 5).
A : ( x1 , x 2 , x3 ) ( x1 , x 2 ).
(1, 2, 6) (1, 2).
2
2
3.
Оператор называется линейным, если дляn
любых векторов x и y пространства R и
любого числа выполняются соотношения:
1) Свойство аддитивности:
A ( x y ) A ( x ) A ( y ).
2) Свойство однородности:
A ( x ) A ( x ).
4.
Пример. Будет ли указанный операторлинейным?
2
2
2
2
A : ( x1 , x 2 ) ( x1 , x 2 , x1 x 2 ).
Пусть x ( x1 , x 2 ), y ( y1 , y 2 ).
Тогда
x y ( x1 y1 , x 2 y 2 ),
A ( x y ) (( x1 y1 ) , ( x 2 y 2 ) , ( x1 y1 ) ( x 2 y 2 ) ),
2
2
2
2
A( x ) A( y ) ( x , x , x x ) ( y , y , y y )
2
1
2
2
2
1
2
2
2
1
2
2
2
1
2
2
( x y , x y , x x y y ).
2
1
2
1
2
2
2
2
2
1
2
2
2
1
Значит, оператор A не является линейным.
2
2
5.
Пример. Будет ли указанный операторлинейным?
A : ( x1 , x 2 , x3 ) ( x1 , x 2 ).
Пусть x ( x1 , x 2 , x3 ), y ( y1 , y 2 , y 3 ).
Тогда
x y ( x1 y1 , x 2 y 2 , x3 y 3 ),
A ( x y ) ( x1 y1 , x 2 y 2 ),
A ( x ) A ( y ) ( x1 , x 2 ) ( y1 , y 2 ) ( x1 y1 , x 2 y 2 ),
Свойство аддитивности выполняется.
6.
x ( x1 , x 2 , x3 ),A ( x ) ( x1 , x 2 ),
A ( x ) ( x1 , x 2 ) ( x1 , x 2 ).
Свойство однородности выполняется.
Значит, оператор A является линейным.
В дальнейшем будем рассматривать
линейные операторы
A:R R .
n
n
7.
Матрица оператораn
Пусть e1 , e2 ,..., en — базис пространства R .
Тогда для любого вектора
x x1e1 x 2 e2 ... x n en .
Если y A ( x ) — линейный оператор, то
A ( x ) A ( x1e1 x 2 e2 ... x n e n )
A ( x1e1 ) A ( x 2 e2 ) ... A ( x n e n )
x1 A ( e1 ) x 2 A ( e2 ) ... x n A ( e n ).
8.
Так както
A ( e1 ), A ( e2 ),..., A ( e n ) R ,
n
A ( e1 ) a11e1 a12 e2 ... a1 n e n ,
A ( e2 ) a 21e1 a 22 e2 ... a 2 n e n ,...,
A ( en ) a n1e1 a n 2 e 2 ... a nn en .
Поэтому
A ( x ) x1 ( a11e1 a12 e 2 ... a1 n e n ) ...
x n ( a n1e1 a n 2 e2 ... a nn en )
( a11 x1 a 21 x 2 ... a n1 x n ) e1 ...
( a1 n x1 a 2 n x 2 ... a nn x n ) e n . (1)
9.
С другой стороны, т.к. y R , тоn
y y1e1 y 2 e2 ... y n e n .
Из (1) и (2) получаем
y1 a11 x1 a21 x2 ... an1 xn ,
y a x a x ... a x ,
2
12 1
22 2
n2 n
............................................
yn a1n x1 a2 n x2 ... ann xn .
(2)
10.
Матрицаa11
a
12
A
...
a1n
a21
a22
...
a2 n
... an1
... an 2
... ...
... ann
называется матрицей линейного
оператора y A ( x ) в базисе e1 , e2 ,..., en .
Любой линейный оператор y A ( x ) можно
записать с помощью матричного уравнения
Y AX .
11.
Замечание. Для того, чтобы найти матрицулинейного оператора, достаточно найти
образы базисных векторов.
Пример. Найти матрицу линейного оператора
A : ( x1 , x 2 , x3 ) (2 x1 , x 2 , x1 x3 )
в базисе (1, 0, 0), (0,1, 0), (0, 0,1).
Решение.
A (1, 0, 0) (2, 0,1), A (0,1, 0) (0, 1, 0), A (0, 0,1) (0, 0,1).
Значит, матрица оператора имеет вид
2 0 0
A 0 1 0 .
1 0 1
12.
Связь между матрицами оператора в разныхбазисах
*
Теорема. Матрицы A и A линейного
оператора в разных базисах связаны
соотношением
1
A C AC ,
*
где C — матрица перехода от старого базиса к
новому.
13.
Пример. Матрица линейного оператора вбазисе e1 , e2 имеет вид
17 6
A
.
6 8
Найти матрицу этого оператора в базисе
e1 2 e2 , 2 e1 e2 .
Решение. Матрица перехода
1 2
C
.
2 1
При этом
1 1 2
C
.
5 2 1
1
14.
Значит,1 1 2 17 6 1 2 5 0
A
.
5 2 1 6 8 2 1 0 20
*







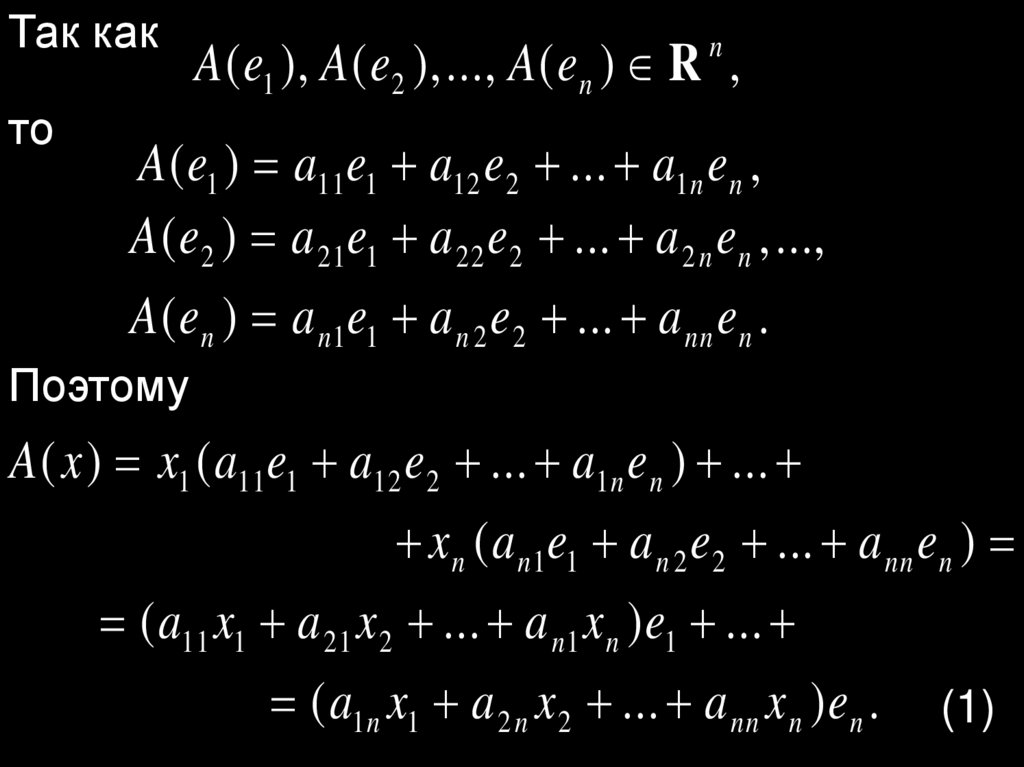






 Математика
Математика








