Построение некоторых правильных многоугольников

1.

2.

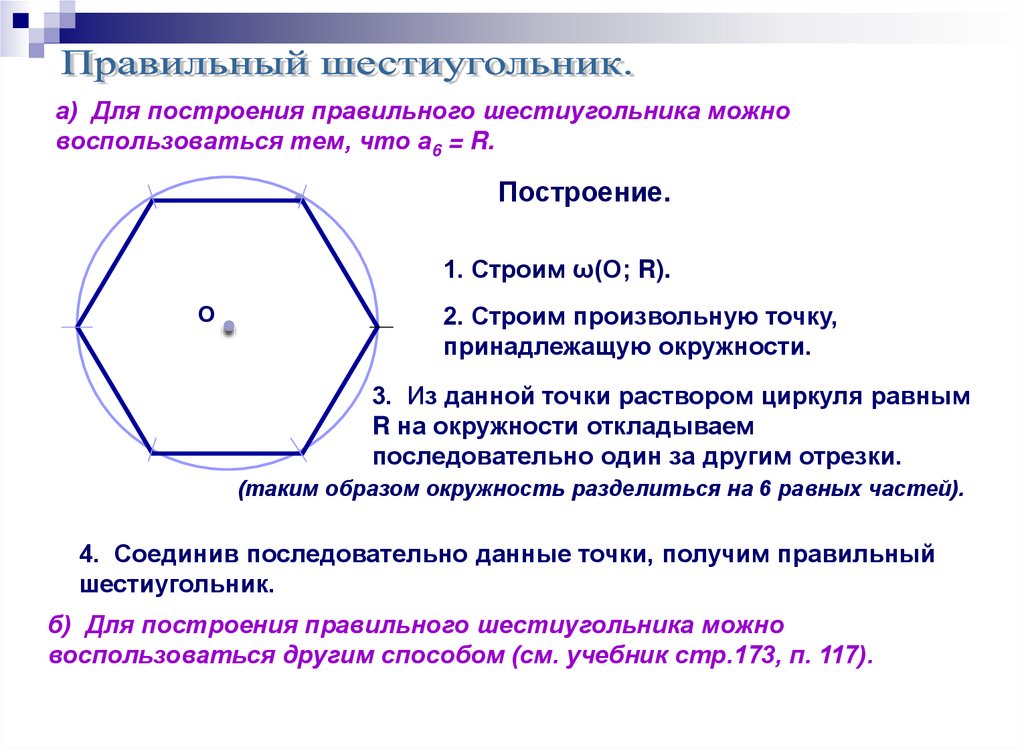
а) Для построения правильного шестиугольника можно
воспользоваться тем, что а6 = R.
Построение.
1. Строим ω(О; R).
О
2. Строим произвольную точку,
принадлежащую окружности.
3. Из данной точки раствором циркуля равным
R на окружности откладываем
последовательно один за другим отрезки.
(таким образом окружность разделиться на 6 равных частей).
4. Соединив последовательно данные точки, получим правильный
шестиугольник.
б) Для построения правильного шестиугольника можно
воспользоваться другим способом (см. учебник стр.173, п. 117).

3.

Для построения правильного треугольника воспользуемся тем же
алгоритмом, что и для построения правильного шестиугольника,
только получив 6 точек на окружности, соединим их через одну.
Построение.
1. Строим ω(О; R).
О
2. Строим произвольную точку,
принадлежащую окружности.
3. Из данной точки раствором циркуля равным
R на окружности откладываем
последовательно один за другим отрезки.
(таким образом окружность разделиться на 6 равных частей).
4. Соединив последовательно через одну данные точки, получим
правильный треугольник.

4.

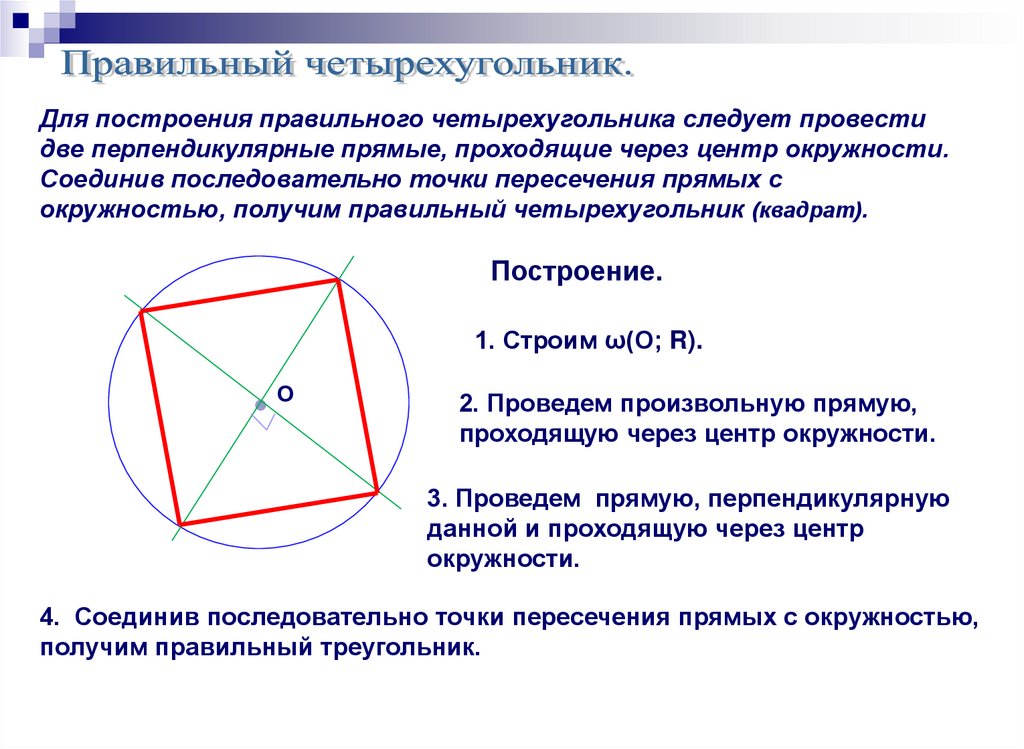
Для построения правильного четырехугольника следует провести
две перпендикулярные прямые, проходящие через центр окружности.
Соединив последовательно точки пересечения прямых с
окружностью, получим правильный четырехугольник (квадрат).
Построение.
1. Строим ω(О; R).
●О
2. Проведем произвольную прямую,
проходящую через центр окружности.
3. Проведем прямую, перпендикулярную
данной и проходящую через центр
окружности.
4. Соединив последовательно точки пересечения прямых с окружностью,
получим правильный треугольник.

5.

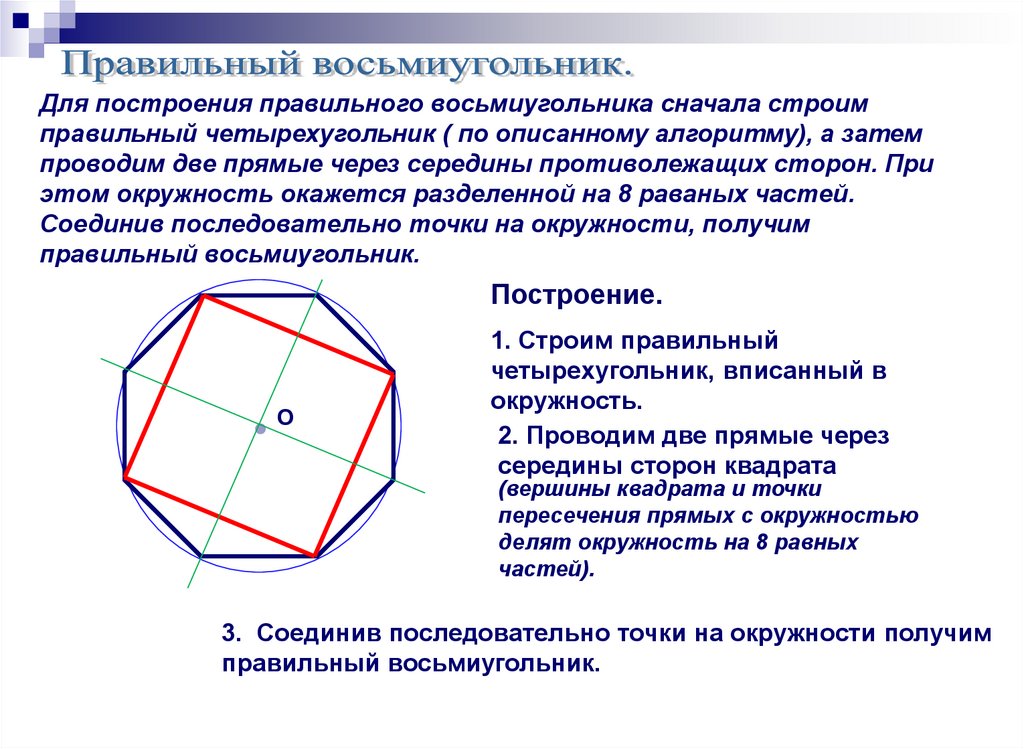
Для построения правильного восьмиугольника сначала строим
правильный четырехугольник ( по описанному алгоритму), а затем
проводим две прямые через середины противолежащих сторон. При
этом окружность окажется разделенной на 8 раваных частей.
Соединив последовательно точки на окружности, получим
правильный восьмиугольник.
Построение.
●О
1. Строим правильный
четырехугольник, вписанный в
окружность.
2. Проводим две прямые через
середины сторон квадрата
(вершины квадрата и точки
пересечения прямых с окружностью
делят окружность на 8 равных
частей).
3. Соединив последовательно точки на окружности получим
правильный восьмиугольник.

6.

Рассмотренные способы построения правильных многоугольников
дают возможность построить многоугольники, вписанные в
окружность. Чтобы построить многоугольник, описанный около
окружности, пользуются теми же способами, только на последнем
этапе не соединяют полученные точки на окружности, а проводят
через них касательные.
Построим правильный шестиугольник, описанный около окружности.
Построение.
1. Строим ω(О; R).
О
2. Строим произвольную точку,
принадлежащую окружности.
3. Из данной точки раствором циркуля равным
R на окружности откладываем
последовательно один за другим отрезки.
4. Через каждую полученную точку на окружности
проводим касательные. Получим правильный
шестиугольник.