Похожие презентации:
Алгебра Буля и нормальные формы
1.
Модуль 2Математическая логика
Занятие 2.4. Алгебра
Буля и нормальные
формы
2022 г.
2.
Содержание1.
2.
3.
4.
5.
Совершенные дизъюнктивные
нормальные формы
Совершенные конъюнктивные
нормальные формы
Двойственность булевых функций
Построение совершенных НФ с
помощью таблиц истинности
Построение совершенных НФ с
помощью аналитического вывода
3.
Булевы функцииВ алгебре Буля используются
только логические переменные,
которые принимают значения либо
0 (ложь), либо 1 (истина)
Функции, которые определены на
этих переменных и принимают
значения 0 или 1, также
называются логическими, или
булевыми
4.
Нормальные формыДля задания логических функций
используют формулы алгебры логики
(аналитическое представление)
Среди формул выделяют :
•дизъюнктивную нормальную форму
(ДНФ)
•конъюнктивную нормальную форму
(КНФ)
5.
Дизъюнктивная НФДизъюнктивная нормальная форма
(ДНФ) – это сумма произведений,
образованных из переменных и их
отрицаний
ДНФ не содержит скобок
Например,
a bc – ДНФ
d( b c )
– нет
6.
Конъюнктивная НФКонъюнктивная нормальная форма
(КНФ) – это произведение сумм,
состоящих из переменных и их
отрицаний
КНФ может содержать скобки
Например,
d ( b c ) – КНФ
a bc – нет
7.
Теорема о ДНФВсякая сложная логическая функция
может быть сведена к ДНФ
1. Записать булеву функцию в виде {+, , -}
2. С помощью законов де Моргана спустить черту
отрицания до отдельных букв и по закону
двойного отрицания уничтожить двойные
отрицания
3. С помощью первого закона дистрибутивности
уничтожим все произведения сумм и проведем
поглощение
8.
Совершенные ДНФЕсли ДНФ функции f1(x1, x2, . . . ,xn) от
n переменных в каждой своей
конъюнкции содержит все n переменных
либо их отрицания, то это совершенная
дизъюнктивная нормальная форма
(СДНФ)
x x
1
2
1
2
x
n
... xn
f 1
, где
i x при 0
i
i
i
x
i x при 1 и
i
i
i
9.
Сов ДНФКаждая функция имеет одну
единственную СовДНФ и она может
быть получена из таблицы
истинности этой функции путем
записи через знак логического
сложения всех наборов
переменных, на которых эта
функция определена, как истинная
10.
Сов ДНФКаждый такой набор переменных
соответствует конъюнкции,
причем если переменная xi =1, то
xi входит в нее без отрицания,
если xi =0, то xi входит в нее с
отрицанием xi к ДНФ
11.
Теорема о КНФВсякая сложная логическая функция
может быть сведена к КНФ
1. Записать булеву функцию в виде {+, , -};
2. С помощью законов де Моргана спустить черту
отрицания до отдельных букв и по закону
двойного отрицания уничтожить двойные
отрицания
3. С помощью второго закона дистрибутивности
уничтожим все суммы произведений и
проведем поглощение
12.
Совершенные КНФЕсли КНФ функции f1(x1, x2, . . . ,xn) от n
переменных в каждой своей дизъюнкции
содержит все n переменных либо их
отрицания, то это совершенная
конъюктивная нормальная форма
(СовКНФ)
1
2
n
&( x1 x2 ... xn ) , где
f 0
x
i x при 1
i
i
i
x
i x при 0 и
i
i
i
13.
Сов КНФКаждая функция имеет одну
единственную СовКНФ и она
может быть получена из таблицы
истинности этой функции путем
записи через знак логического
умножения всех наборов
переменных, на которых эта
функция определена, как ложная
14.
Сов КНФКаждый такой набор переменных
соответствует дизъюнкции,
причем если переменная xi =0, то
xi входит в нее без отрицания,
если xi =1, то xi входит в нее с
отрицанием xi
15.
ПримерыДНФ:
КНФ:
a +bc
(a +b)c
abc + b c
ab(c + b)
a
c
b
a
с + b
с + b
16.
Двойственные функцииДана булева функция f(x1, x2,…, xn)
Тогда функция f* называется
двойственной к функции f
f * ( x1 , x2 ,..., x n ) f ( x1 , x2 ,..., x n )
17.
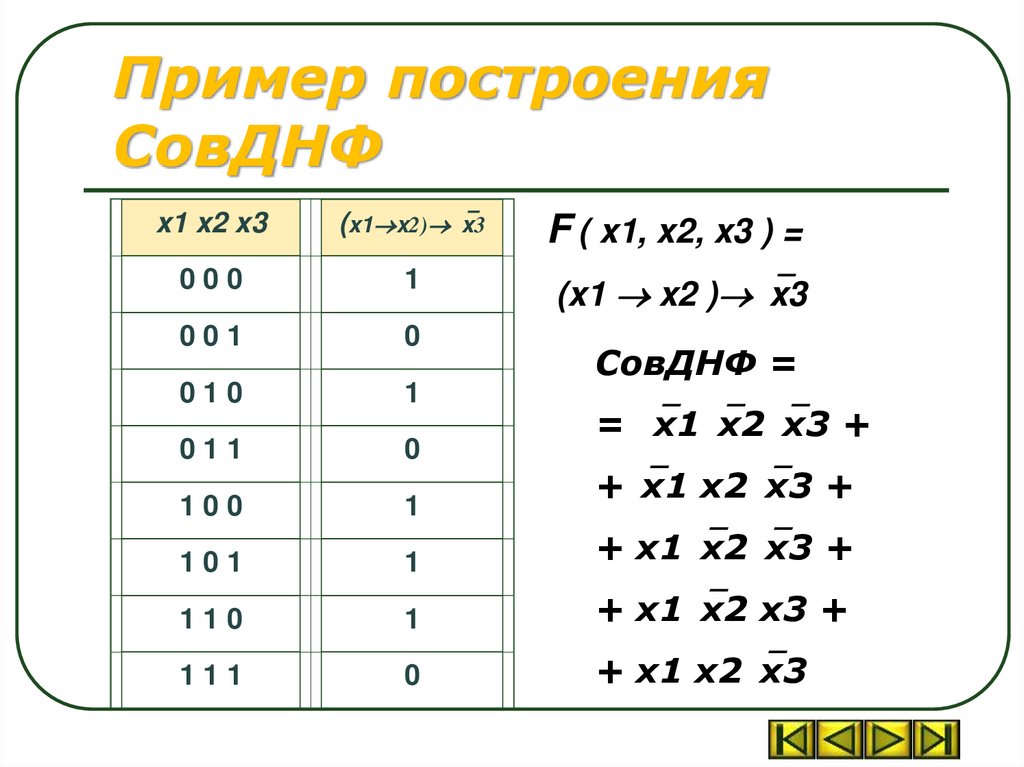
Пример построенияСовДНФ
x1 x2 x3
(x1 x2) x3
F ( x1, x2, x3 ) =
000
1
(x1 x2 ) x3
001
0
010
1
011
0
100
1
101
1
+ x1 x2 x3 +
110
1
+ x1 x2 x3 +
111
0
+ x1 x2 x3
СовДНФ =
= x1 x2 x3 +
+ x1 x2 x3 +
18.
Аналитический выводСовДНФ
( x1 x2 ) x3 ( x1 x2 ) x3 x1 x2 x3
x1 x2 x3 x1 x2 1 1 1 x3
x1 x2 ( x3 x3 ) ( x1 x1 ) ( x2 x2 ) x3
x1 x2 x3 x1 x2 x3 x1 x2 x3
x1 x2 x3 x1 x2 x3 x1 x2 x3
x1 x2 x3 x1 x2 x3 x1 x2 x3
x1 x2 x3 x1 x2 x3
19.
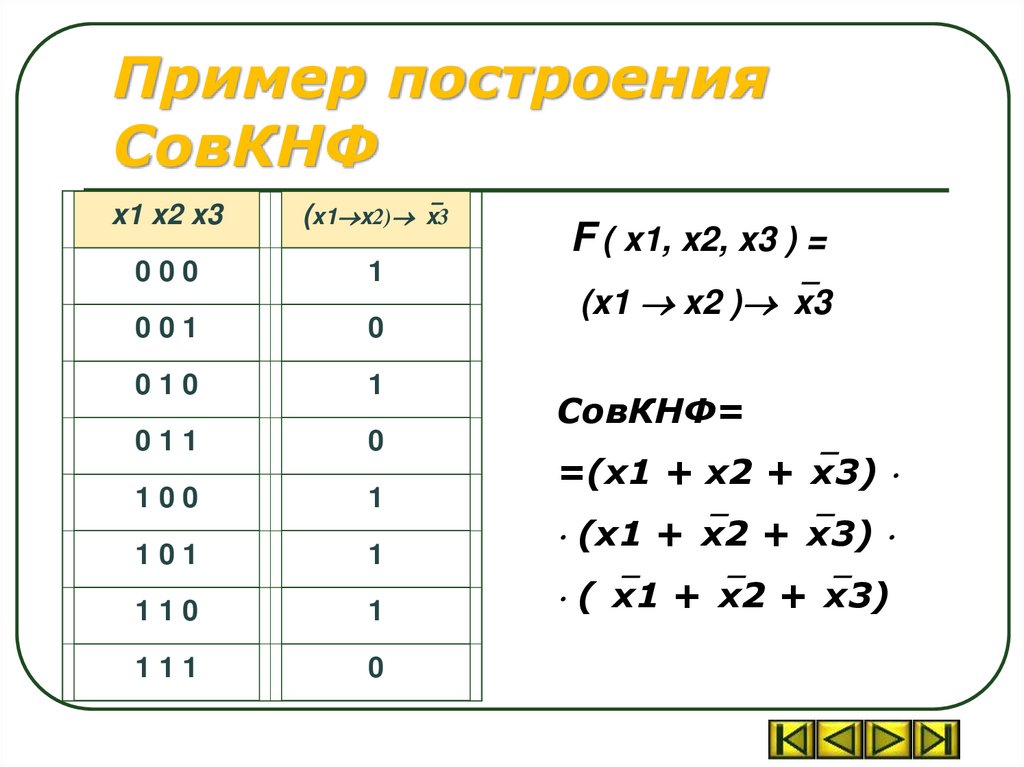
Пример построенияСовКНФ
x1 x2 x3
(x1 x2) x3
000
1
001
0
010
1
011
0
100
1
101
1
110
1
111
0
F ( x1, x2, x3 ) =
(x1 x2 ) x3
СовКНФ=
=(x1 + x2 + x3)
(x1 + x2 + x3)
( x1 + x2 + x3)
20.
Аналитический выводСовКНФ
( x1 x2 ) x3 ( x1 x2 ) x3 x1 x2 x3
x1 x2 x3 ( x1 x3 ) ( x2 x3 )
( x1 0 x3 ) (0 x2 x3 )
( x1 x2 x2 x3 ) ( x1 x1 x2 x3 )
( x1 x2 x3 ) ( x1 x2 x3 ) ( x1 x2 x3 )
( x1 x2 x3 ) ( x1 x2 x3 ) ( x1 x2 x3 ) ( x1 x2 x3 )
21.
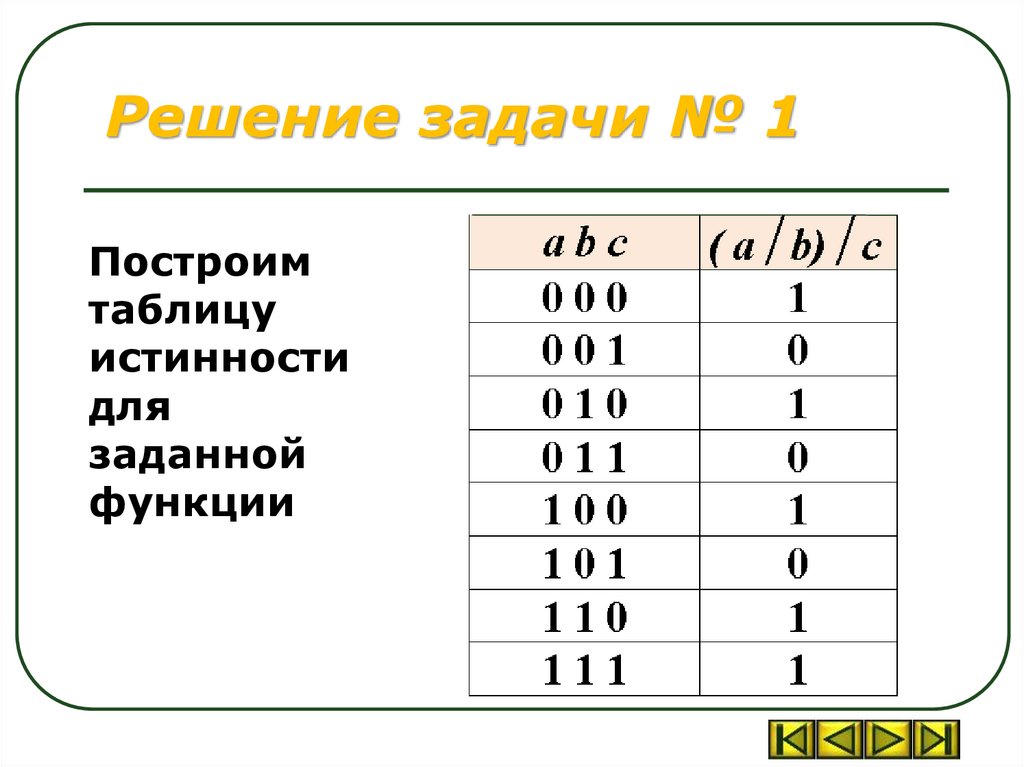
Задача № 1Построить СовДНФ и СовКНФ
для функции (a| b)| c
Минимальная ДНФ
штриха Шеффера:
a| b a b
22.
Решение задачи № 1Построим
таблицу
истинности
для
заданной
функции
23.
Решение задачи № 1Совершенные формы функции
СовДНФ = a b c + a b c + a b c + a b c + a b c
СовКНФ = (a + b + c) (a + b + c) ( a + b + c)
24.
Аналитический выводСовДНФ для задачи № 1
(a b ) c ( a b ) c a b c
a b c a b c a b c a b c a b c
25.
Аналитический выводСовКНФ для задачи № 1
(a b ) c ( a b ) c a b c
(a c ) (b c ) (a b b c ) (a a b c )
(a b c ) (a b c ) (a b c )
26.
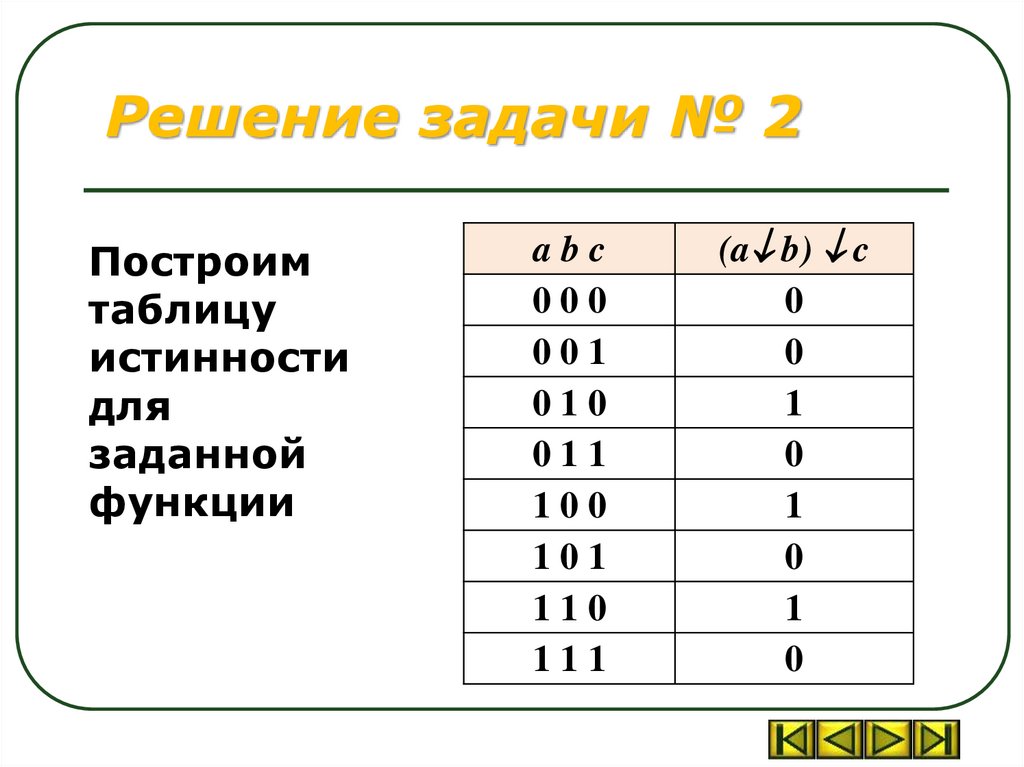
Задача № 2Построить СовДНФ и СовКНФ
для функции (a b) c
Минимальная ДНФ
функции Пирсона (иначе,
элемента Вебба):
a b a b a b
27.
Решение задачи № 2Построим
таблицу
истинности
для
заданной
функции
abc
000
001
010
011
100
101
110
111
(a b) c
0
0
1
0
1
0
1
0
28.
Решение задачи № 2Совершенные формы функции
СовДНФ =
ab c +a b c +a b c
СовКНФ = (a b c) (a + b + c) (a + b + c)
( a + b + c ) (a b c )
29.
Аналитический выводСовДНФ для задачи № 2
(a b) c (a b) c (a b) c
a ( b b) c ( a a) b c
ab c +a b c +a b c
30.
Аналитический выводСовКНФ для задачи № 2
(a b) c a b c ( a b ) c
( a + b +c c)(a a + b b + c)
( a + b +c )(a + b + c)(a + b + c)
( a + b + c)( a + b + c)
31.
Задача № 3Построить СовДНФ и СовКНФ
для функции
( a b) c
Минимальная ДНФ
импликации:
a b a b
32.
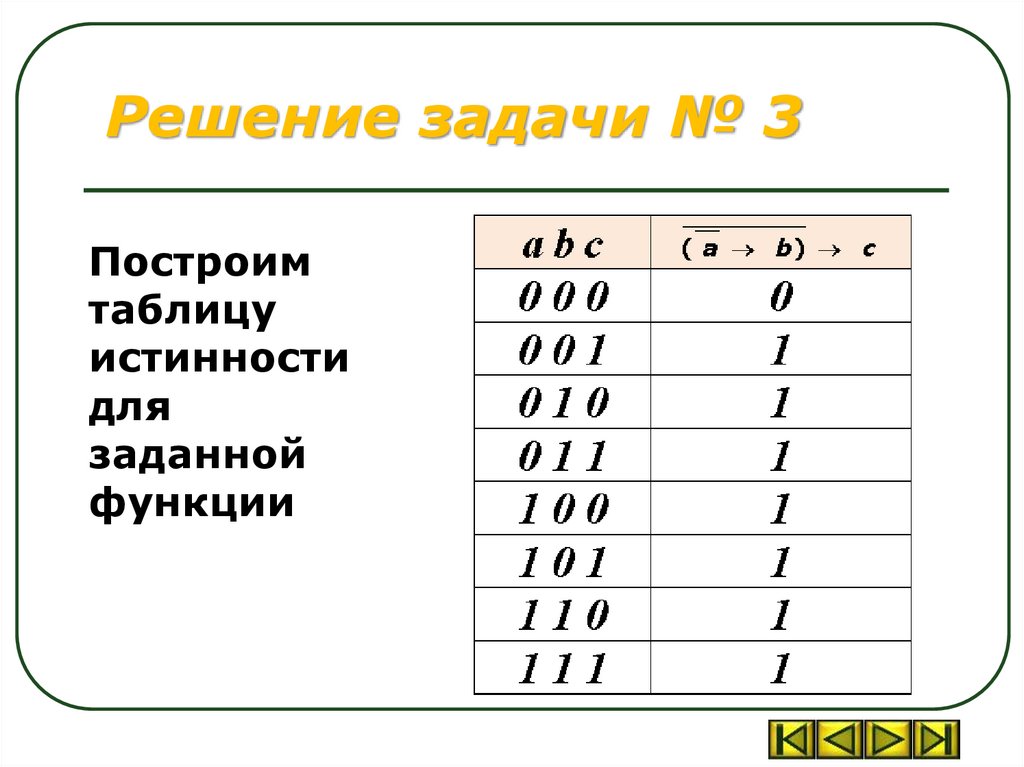
Решение задачи № 3Построим
таблицу
истинности
для
заданной
функции
33.
Решение задачи № 3Совершенные формы функции
СовДНФ =
a b c +abc a b c + a b c + a b c + a b c + a b c
СовКНФ = a + b +c




























 Математика
Математика








