Формальные теории и исчисления

1.

Модуль 3
Формальные теории и
исчисления
Занятие 3.1. Исчисление
высказываний
2022 г.

2.

Содержание
1.
2.
3.
4.
Понятие формальной теории
Исчисление высказываний: алфавит,
формулы, аксиомы и правило
вывода
Основные математические приемы:
правило подстановки и теорема
дедукции
Свойства исчисления высказываний

3.

.
Формальная теория
множество А символов, образующих
алфавит
множество слов F в алфавите А, которые
называются формулами
подмножество В формул, B F
которые называются аксиомами
множество R отношений на множестве
формул R F n 1, которые называются
правилами вывода

4.

Ограничения (1)
Алфавит A может быть конечным или
бесконечным
Множество формул F обычно задается
индуктивно, как правило, оно бесконечно
Множества
A и F по совокупности
определяют язык формальной теории,
или сигнатуру

5.

Ограничения (2)
Множество аксиом
B может быть
конечно или бесконечно
Бесконечное множество
аксиом B ,
как правило, задают в виде
конечного множества схем и правил
порождения из этих схем
конкретных аксиом
Множество
правил
обычно конечно
вывода
R

6.

Свойства формальной
теории
выводимость
интерпретация
общезначимость
разрешимость
непротиворечивость
полнота
независимость

7.

Выводимость
Пусть F1 , F2 , Fn , G - формулы теории Т,
т.е.
F1 , F2 , Fn , G F
Если существует такое правило вывода R, что
( F1 , F2 , Fn , G ) R
, то говорят, что формула G
непосредственно выводима из формул F , F , F
1
по правилу вывода R:
F1 , F2 , Fn
R
G
где формулы F называются посылками,
заключением
2
n
а формула G

8.

Вывод, гипотеза,
теорема
Вывод формулы G из формул – F1 , F2 , ..., Fn – это
такая последовательность формул , что Fn=G , а
любая формула Fi - либо аксиома, либо исходная
формула, либо непосредственный вывод из ранее
полученных формул
Если в теории Т существует вывод формулы G из
формул , то записывают
F1 , F2 , ..., Fn ├ G, где –
F1 , F2 , ..., Fn - гипотезы
Теорема – формула, выводимая только из аксиом,
без гипотез

9.

Интерпретация
Интерпретацией формальной теории T в
область интерпретации M называется
функция, h:F→M, которая каждой формуле F
теории T однозначно сопоставляет некое
содержательное высказывание относительно
объектов множества M
Высказывание может быть истинно или
ложно, или не иметь истинностного значения.
Если оно истинно, то говорят, что формула
выполняется в данной интерпретации

10.

Интерпретация
Например, припишем значение 0 или 1 атомарным
формулам (простым высказываниям), которые
входят в сложные, что будет называться
интерпретацией h
Говорят, что формула A исчисления истинна при
некоторой интерпретации h тогда и только тогда,
когда h(А)=1, в противном случае говорят, что А
ложна при интерпретации h

11.

Разрешимость
Формальная теория Т называется
разрешимой, если существует
алгоритм, который для любой формулы
теории определяет, является она
теоремой или нет

12.

Алгоритм
Под алгоритмом в интуитивном
смысле мы понимает такую
последовательность действий,
выполнение которых позволяет
получить решение задачи регулярным
путем за конечное число шагов

13.

Свойства алгоритма
1. дискретность шагов
2. детерминируемость
3. регулярность
4. конечность
5. массовость

14.

Алгоритм
Например, правила дорожного
движения не являются алгоритмом, т.к.
содержат неоднозначность
Ярким примером такой
неоднозначности может служить
дорожный знак «прямо и
направо»

15.

Общезначимость
Формула общезначима (тавтология), если
она истинна в любой интерпретации
Формула называется противоречием,
если она ложна в любой интерпретации

16.

Непротиворечивость
Формальная теория семантически
непротиворечива, если ни одна из ее
теорем не является противоречием
Формальная теория формально
непротиворечива, если в ней не
являются выводимыми одновременно
формулы F и F

17.

Полнота и
независимость
Формальная теория называется полной,
если каждому истинному высказыванию
соответствует теорема Т
Система аксиом формальной
теории называется независимой, если
ни одна из аксиом не выводится из
оставшихся

18.

.
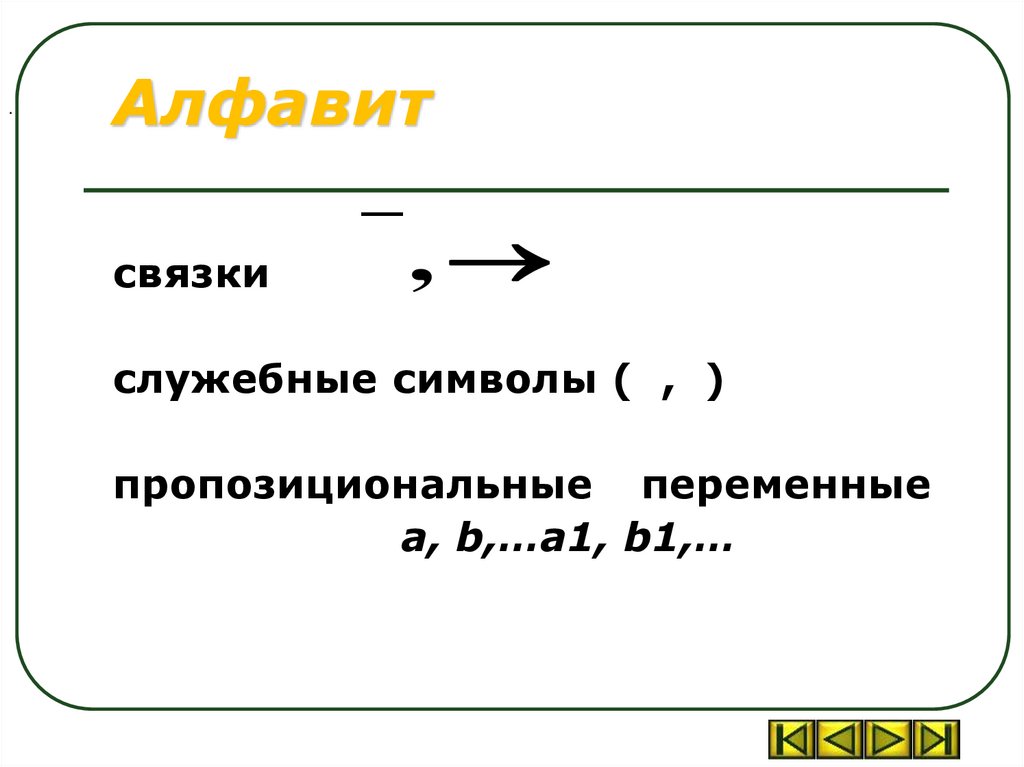
Алфавит
связки
,
служебные символы ( , )
пропозициональные переменные
a, b,…a1, b1,…

19.

Формулы
1. Переменные суть формулы
2. Если А, В формулы, то
( A ), ( A B ) - тоже формулы

20.

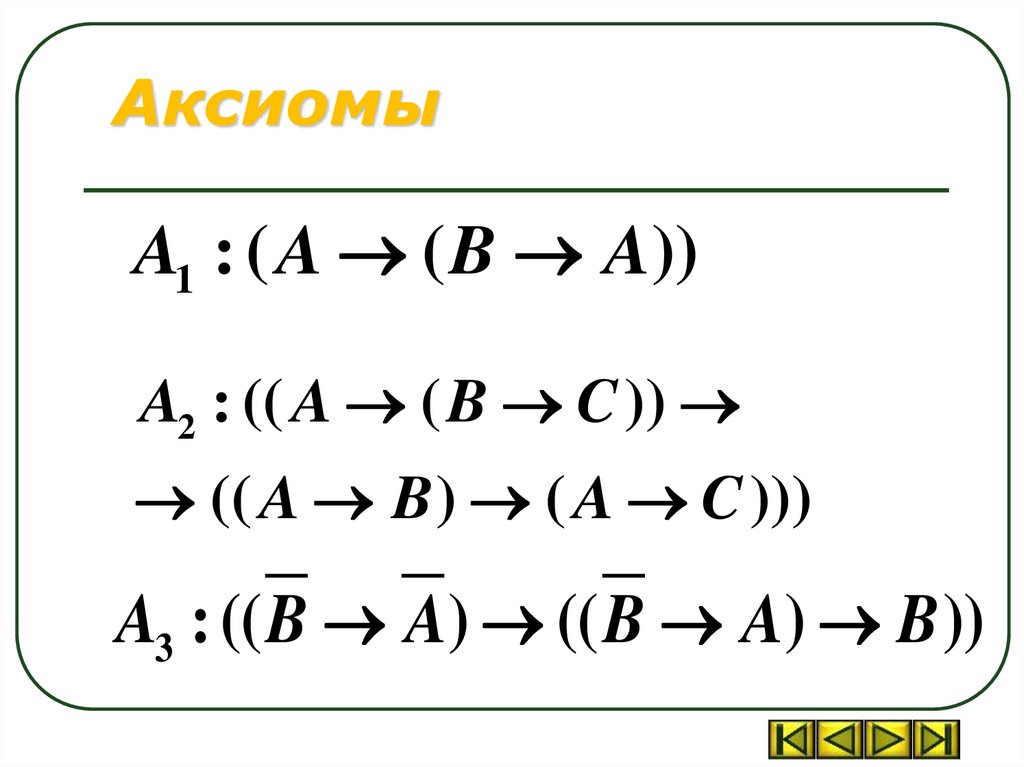
Аксиомы
A1 : ( A ( B A))
A2 : (( A ( B C ))
(( A B ) ( A C )))
A3 : (( B A) (( B A) B ))

21.

Правило вывода
A, A B
Modus _ ponens
B
правило отделения или
правило заключения (MP)

22.

Интерпретация
Функция h называется интерпретацией,
если для любых формул А и В исчисления
высказываний h удовлетворяет
следующим условиям
h( A) h( A)
h( A B ) h( A) h( B )

23.

Истинность и ложность
Формула А исчисления
высказываний истинна при
некоторой интерпретации h тогда
и только тогда, когда h(A)=1
В противном случае, говорят, что
А ложна при интерпретации h

24.

Тавтология и
противоречие
Формула А исчисления высказываний
является тавтологией, тогда и только
тогда, когда она истинна независимо от
интерпретации
Формула А называется противоречием,
тогда и только тогда, когда она ложна при
любой интерпретации

25.

Пример № 1
Проверить, что формула R
является тавтологией
R ( A B) A B

26.

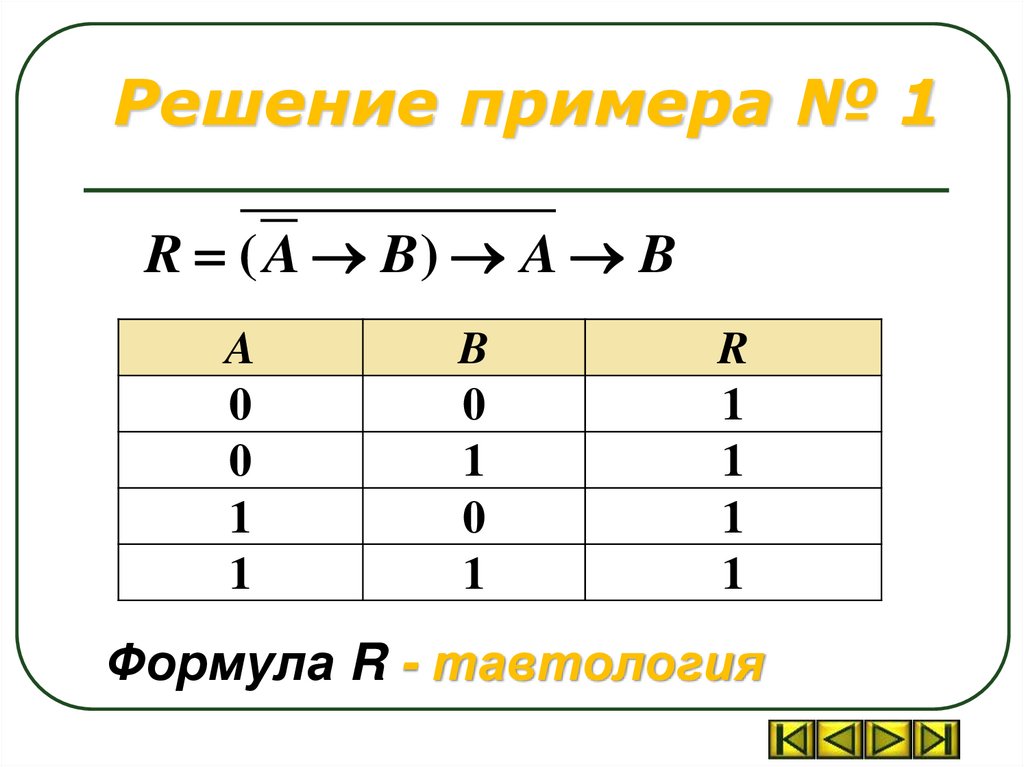
Решение примера № 1
R ( A B) A B
A
0
0
1
1
B
0
1
0
1
R
1
1
1
1
Формула R - тавтология

27.

Правило подстановки
Пусть А – некая формула, выводимая
(доказуемая) в исчислении
высказываний, х- переменная,
В – любая формула исчисления
высказываний
Тогда формула, которая получается из
формулы А путем подстановки в нее
вместо переменной х формулы В,
выводима (доказуема)
А(……х…..)(B//x)

28.

Пример № 2
Проверить, что формула
выводима в исчислении
высказываний
А→А

29.

Решение примера № 2
1. Подставим в аксиому А2 вместо В
(А→А), вместо С подставим А
( A (( A A) A)) (( A ( A A)) ( A A))
2. Применив аксиому А1, и по правилу
заключения получаем
( A ( A A)) ( A A)
3. Применив аксиому А1 и по правилу
заключения получаем ( A A)

30.

Теорема
Каждая формула,
доказуемая в исчислении
высказываний,
тождественно истинна в
алгебре высказываний

31.

Пример № 3
Каждая аксиома – тождественно истинная
Правило подстановки, примененное к
тождественно истинным формулам,
приводит к тождественно истинным
формулам
Правило заключения, примененное к
тождественно истинным формулам,
приводит к тождественно истинным
формулам

32.

Теорема дедукции
Если Г – множество формул,
А и В – формулы из Г высказываний,
и А├В, то Г├А→В, т.е. в Г выводима
формула
А→В

33.

Пример № 4
Проверить, что из А→В, В→С
формула А→С выводима в
исчислении высказываний, т.е.
А→В, В→С ├ А→С

34.

Решение примера № 4
1.
А→В –гипотеза
2.
В→С - гипотеза
3.
А - тоже гипотеза
4.
В выводимо по правилу заключения из
5.
6.
п. 1 и п. 3
С выводимо по правилу заключения из
п. 2 и п. 4
Следовательно, А→В, В→С А├С, и , по
теореме о дедукции, А→В, В→С ├А→С

35.

Разрешимость и
независимость
Проблема разрешимости для
исчисления высказываний
разрешима
Система аксиом исчисления
высказываний независима

36.

Полнота и
непротиворечивость
Исчисление высказываний полно в узком
смысле, т.е. к системе аксиом нельзя
добавить в качестве новой аксиомы
недоказуемой в этом исчислении формулы
Исчисление высказываний полно в
широком смысле, т.е. всякая тождественно
истинная формула алгебры высказываний
доказуема в исчислении высказываний
Исчисление высказываний
непротиворечиво

37.

Исчисление высказываний
по Гильберту и Аккерману
Связки ,
( A B A B)
Аксиомы A A A
A В В A
A A В
(В С ) ( A В A С )
Правило вывода
МР

38.

Свойства исчисление
высказываний (ИВ)
Исчисление высказываний:
Разрешимо
Полно
Непротиворечиво
Система аксиом ИВ независима
Интерпретацией
ИВ
являются
алгебра
высказываний (АВ) и алгебра Буля (АБ)
Выводимые формулы
истинны в АВ и АБ
в
ИВ
тождественно