Системы двух линейных уравнений с двумя переменными. Урок №14. Основные понятия. Алгебра. 7 класс

1.

7 класс
алгебра
Системы двух линейных уравнений
с двумя переменными
Урок № 14
Основные понятия.
1

2.

Цели:
Сформировать представление о математической
модели система уравнений.
Познакомиться с понятием системы двух
линейных уравнений и ее решении.
Изучить графический способ решения систем двух
уравнений.
Вопрос о количестве решений системы двух
линейных уравнений с двумя переменными.
Решение более сложных систем двух уравнений с
двумя
неизвестными. www.konspekturoka.ru
12.09.2012
2

3.

Вспомним!
Уравнение вида: aх + b = 0
называется линейным уравнением
с одной переменной (где х – переменная,
а и b некоторые числа).
Внимание!
х – переменная входит в уравнение
обязательно в первой степени.
45 x - 18 = 0
линейное уравнением
с одной переменной
3х² + 6х + 7 = 0
не линейное уравнением
с одной переменной
www.konspekturoka.ru
12.09.2012
3

4.

Вспомним!
Линейное уравнение с
двумя переменными
Уравнение вида:
называется линейным уравнением с
двумя переменными (где х, у - переменные,
а, b и с - некоторые числа).
Решением уравнения с двумя
неизвестными называется пара
переменных, при подстановке
которых уравнение становится
верным числовым равенством.
12.09.2012
www.konspekturoka.ru
4

5.

Вспомним!
Решить линейное уравнение –
это значит найти те значения
переменной, при каждом из которых
уравнение обращается в верное
числовое равенство.
Таких решений бесконечно много.
12.09.2012
www.konspekturoka.ru
5

6.

Вспомним!
Реальная ситуация
(словесная модель)
Сумма двух чисел
равна 3.
х +у–3=0
Алгебраическая
модель
Геометрическая
модель
х+у=3
(линейное
уравнение с двумя
переменными)
прямая т
(график линейного
уравнения с двумя
переменными)
Теорема:
Графиком любого линейного уравнения
ах + by + c = 0 есть прямая.
Для построения графика достаточно найти
координаты двух точек.
12.09.2012
www.konspekturoka.ru
6

7.

Вспомним!
Алгоритм построения графика
уравнения ах + bу + c = 0
1. Придать переменной х конкретное значение х₁; найти
из уравнения ах + bу + c = 0 соответствующее значение у₁.
Получим (х₁;у₁).
2. Придать переменной х конкретное значение х₂; найти
из уравнения ах + bу + c = 0 соответствующее значение у₂.
Получим (х₂;у₂).
3. Построим на координатной плоскости точки (х₁; у₁),
(х₂; у₂) и соединим прямой.
4. Прямая – есть график уравнения.
12.09.2012
www.konspekturoka.ru
7

8.

Часто приходится рассматривать математическую модель
состоящую из двух линейных уравнений с двумя переменными.
{ a х+b y+c =0
a1 x + b1 y + c1 = 0
2
2
2
Решение системы уравнений с двумя неизвестными
называется пара переменных, при подстановке
которых уравнения становятся верными
числовыми равенствами.
Решить систему - это значит найти все ее решения
или доказать, что их нет.
12.09.2012
www.konspekturoka.ru
8

9.

Решить систему уравнений:
{
2x - y - 3 = 0,
х + 2y - 4 = 0.
y
Пример 1
Графический способ
решения систем
у=
Построим график уравнения
–у–3=0,
у = 2х – 3.
х
у
1
-1
2
1
(-х
Получим точки:
(1; -1), (2; 1)
1 2
-1 (1; -1)
2
1
Получим точки:
(0; 2), (2; 1)
Прямые пересекаются в
динственной точке А(2;1)
12.09.2012
-3
у
(2; 1)
x
-3
2х
2
А
у=
0
:2
2
(0; 2) 1
O
Построим график уравнения
+ 2у – 4 = 0 , 2у = -х + 4,
= (-х + 4) : 2.
х
+4 )
Ответ: (2; 1)
www.konspekturoka.ru
9

10.

Количество решений двух линейных уравнений с
двумя переменными.
{ a х+b y+c =0
a1 x + b1 y + c1 = 0
2
2
2
а1 b1
1 )Если
≠ , то прямые пересекаются и система
а 2 b2 имеет единственное решение.
а1 b1 c1
2 )Если
=
≠ , то прямые параллельны и система не
а 2 b2 c 2 имеет решений. Система называется
несовместной.
а1 b1 c1
3 )Если
=
= , то прямые совпадают и система
а 2 b2 c 2 имеет бесконечно много решений.
Система называется
неопределенной.
12.09.2012
www.konspekturoka.ru
10

11.

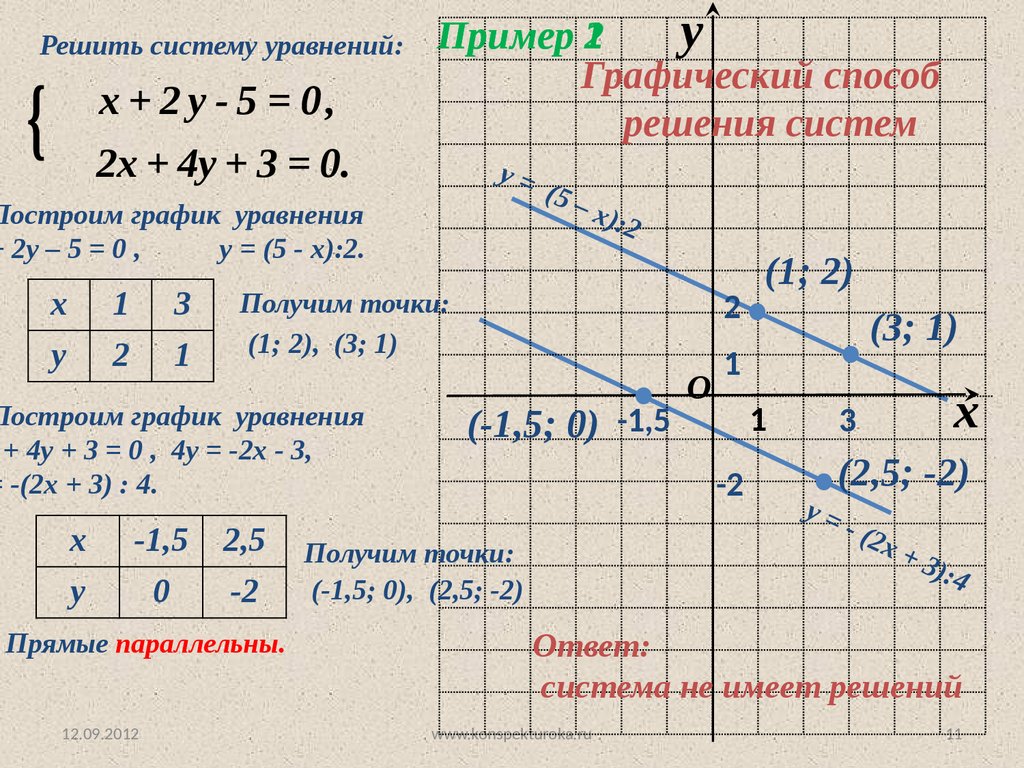
Решить систему уравнений:
{
x + 2 y - 5 = 0,
2х + 4y + 3 = 0.
y
Пример 21
Графический способ
решения систем
у=
Построим график уравнения
+ 2у – 5 = 0 ,
у = (5 - х):2.
х
у
1
2
3
1
-1,5
0
2,5
-2
Прямые параллельны.
12.09.2012
х):2
Получим точки:
(1; 2), (3; 1)
Построим график уравнения
+ 4у + 3 = 0 , 4у = -2х - 3,
= -(2х + 3) : 4.
х
у
(5 –
2
(-1,5; 0) -1,5
O
(3; 1)
1
1
-2
Получим точки:
(-1,5; 0), (2,5; -2)
(1; 2)
x
3
у=
(2,5; -2)
- (2
х+
3):4
Ответ:
система не имеет решений
www.konspekturoka.ru
11

12.

Пример 3
При каких значениях а система уравнений имеет единственное решение:
{ (a + 2)х + 2y = 5a - 3.
( 2 a - 1) x + 3 y = 7 a + 1 ,
Решение
Условие при которых система уравнений имеет единственное решение:
2а - 1 3
≠ ,
а+2 2
Используем свойство пропорции:
2(2a - 1) ≠ 3(a + 2),
4a - 2 ≠ 3a + 6
4a - 3a ≠ 2 + 6
a≠8
Ответ: при всех значениях а, кроме а = 8, данная
функция имеет единственное
решение.
12.09.2012
www.konspekturoka.ru
12

13.

Пример 4
При каких значениях а система уравнений несовместна:
{ (2a + 1)х + 5y = 5a - 3.
( 2 a - 1) x + 3 y = 7 a + 1 ,
Решение
Условие при которых система уравнений несовместна:
2а - 1 3 7 a + 1
= ≠
2а + 1 5 5 a - 3
1) Сначала рассмотрим равенство
2а - 1 3
=
2а + 1 5
Используем свойство пропорции:
5(2a - 1) = 3(2a + 1),
10a - 5 = 6a + 3
12.09.2012
10a - 6a = 3 + 5
www.konspekturoka.ru
4a = 8
a=2
13

14.

2) Теперь проверим неравенство:
3 7a + 1
≠
5 5a - 3
При подстановке значения а = 2 имеем:
3 15
≠
5 7
3 7 •2+1
≠
5 5•2-3
- верное неравенство
Ответ: при а = 2, данная система несовместна.
12.09.2012
www.konspekturoka.ru
14

15.

Пример 5
При каких значениях а система уравнений неопределенна:
{ (a + 1)х + 6y = 11a + 5.
( 2 a - 1) x + 3 y = 7 a + 1 ,
Укажите решения системы.
Решение
Условие при которых система уравнений неопределенна:
2а - 1 3 7 a + 1
= =
а + 1 6 11a + 5
1) Сначала рассмотрим равенство
Используем свойство пропорции:
4a - 2 = a + 1
12.09.2012
2а - 1 3
=
а+1 6
2а - 1 1
=
а+1 2
2(2a - 1) = a + 1 ,
4a - a = 1 + 2
www.konspekturoka.ru
3a = 3
a=1
15

16.

2) Теперь проверим равенство:
3 7a + 1
=
6 11a + 5
При подстановке значения а = 1 имеем:
1 1
=
2 2
3 7 •1+1
≠
6 11 • 1 + 5
- верное равенство
Итак при а = 1, данная система неопределенна.
При подстановке значения а = 1 в данную систему имеем:
{ (1 + 1)х + 6y = 11 • 1 + 5.
( 2 • 1 - 1) x + 3 y = 7 • 1 + 1 ,
Поделим второе уравнение на 2, имеем:
{ 2 х + 6y = 16.
x + 3 y = 8,
{ х + 3y = 8.
x + 3 y = 8,
Ответ: решением системы будет любая пара чисел х и у,
в которой х = 8 – 3у, а у – произвольное число.
12.09.2012
www.konspekturoka.ru
16

17.

Ответить на вопросы
а) что собой представляют графики обоих уравнений
системы?
б) в каком случае система имеет единственное
решение?
в) какая система является несовместимой?
г) о какой системе говорят, что она неопределенна?
д) что называется решением системы уравнений с
двумя переменными?
е) что значит решить систему уравнений?
12.09.2012
www.konspekturoka.ru
17

18.

Спасибо за внимание!
12.09.2012
www.konspekturoka.ru
18