Математический маятник и его виды. Измерение своего роста с помощью математического маятника

1.

Индивидуальный проект
по физике
«Математический маятник и
его виды. Измерение
своего роста с помощью
математического маятника»
Выполнил: студент группы№88 Карпенко Максим
Руководитель: Денисова Наталья Васильевна

2.

Актуальность
В этом году, повторяя тему «Механические
колебания»,
мы
рассматривали
колебательные движения на примере двух
маятников - нитяного и пружинного.
Узнали, какими основными физическими
величинами характеризуется колебательное
движение:
периодом,
частотой
и
амплитудой. Формулы периодов были даны
без выводов, без объяснений, почему такая
зависимость от длины и ускорения
свободного
падения,
например,
для
нитяного маятника.

3.

Цель исследования
Изучение теоретических основ
колебательного движения

4.

Задачи исследования
1.
Изучить учебную литературу о колебаниях.
2.
Проследить историю маятников.
3.
Изучить методику проведения экспериментов.
4.
Провести эксперименты и сделать выводы.

5.

Этапы исследования
1.
Изучение и анализ литературы по этой теме.
2.
Проведение экспериментов.
3.
Систематизация работы.
4.
Подбор наглядного материала. Написание работы.

6.

Математический маятник
Материальную точку с массой,
подвешенную на тонкой нерастяжимой
невесомой, колеблющуюся в поле
тяготения Земли.

7.

Галилео Галилей(1564-1642)
Великий итальянский учёный –
один из создателей точного
естествознания. Родился в городе
Пизе.
Учился
сначала
в
монастырской школе, а затем в
университете. Уже в студенческие
годы
Галилей
увлекался
изучением
колебаний.
Он
обнаружил,
что
колебания
маятника не зависят от его массы,
а определяется длиной подвеса.

8.

Гюйгенс Христиан (1629 – 1695)
Формула
периода
колебаний
математического маятника впервые была
получена на опыте голландским учёным Х.
Гюйгенсом, современником И. Ньютона. В
1656 году в возрасте 27 лет Гюйгенсом
были
сконструированы
первые
маятниковые
часы
со
спусковым
механизмом. Создание часов, измеряющих
время с невиданной точностью, имело
далеко идущие последствия для развития
физического эксперимента и практической
деятельности человека. До этого, время
измеряли по истечению воды. Горению
факела или свечи.

9.

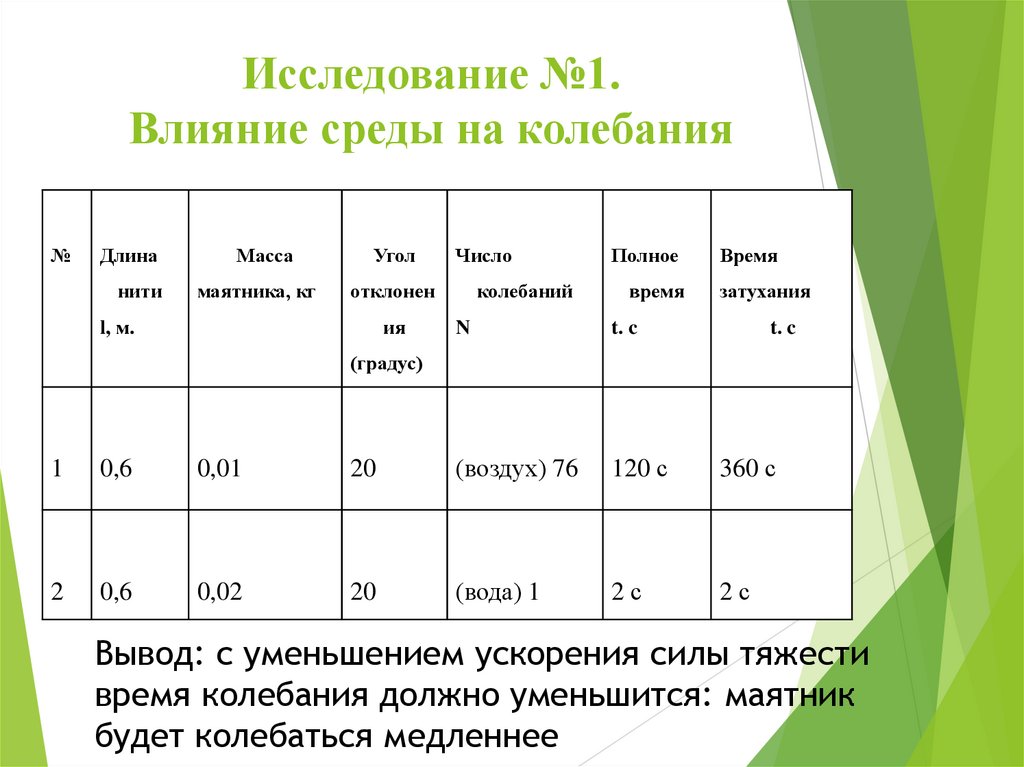
Исследование №1.
Влияние среды на колебания
№
Длина
Масса
Угол
нити
маятника, кг
отклонен
l, м.
ия
Число
колебаний
Полное
время
N
t. c
Время
затухания
t. c
(градус)
1
0,6
0,01
20
(воздух) 76
120 с
360 с
2
0,6
0,02
20
(вода) 1
2с
2с
Вывод: с уменьшением ускорения силы тяжести
время колебания должно уменьшится: маятник
будет колебаться медленнее

10.

Исследование №2.
Нахождение роста с помощью
математического маятника
Сначала я отмерил свой
рост.
Я подошёл к двери,
положил карандаш к ней
и сделал отметку.
Затем я отрезал ленту
такой же длины, что и
мой рост, прикрепил к
ней грузик и повесил с
помощью скотча в
дверной проём.
Я отсчитал время за 10 и
15 колебаний

11.

N
10
10
15
t
26 сек
27 сек
30 сек
По формуле я начал производить расчёты, но с первого
раза у меня не вышло так, как я взял слишком большую
амплитуду, а нужно взять примерно 2-3 см от
положения равновесия шарика
T=t/N=27/10=2,7с
l=(T^2*g)/〖4π〗^2 =1,83 м
Но со второго раза у меня получилось 1,83м.
Расчёты верны так, как мой рост 183см

12.

Практическое
использование колебаний
маятника
1.
Маятники используются для регулировки хода часов,
поскольку любой маятник имеет вполне
определённый период колебаний.
2.
Ускорение свободного падения меняется с
географической широтой, так как плотность земной
коры различна. В районах, где залегают плотные
породы, ускорения несколько больше. Прибор с
маятником применили для разведки полезных
ископаемых. Подсчитав число качаний, можно
обнаружить в земных недрах руды или уголь.
3.
С помощью математического маятника я измерил
свой рост ( так как период колебаний зависит от
длины маятника).

13.

Это интересно…
1.
О маятнике, его роли и влиянии на жизнь и судьбу
человека, писали многие философы и великие учёные:
Аристотель, Плутарх, Платон, Сократ, Архимед.
2.
С помощью маятника однажды удалось отыскать
пропавшего ребёнка. Это произошло в 1934 году.
Малыша на глазах у многих свидетелей унёс орёл. После
того как полицией были предприняты безуспешные
попытки отыскать его, было решено прибегнуть к
помощи маятника, который стали раскачивать над
картой, и в том месте, где амплитуда его колебаний
достигла максимальной силы, было решено искать
ребёнка. К удивлению многих, именно там оказался
пропавший мальчик. Эти сенсационные факты были
опубликованы в швейцарской газете «Трибюн де
Женев».

14.

Заключение
1.При
небольших
отклонениях
от
положения равновесия период не зависит
от амплитуды колебаний маятника (∆t = ±
0,1 секунды);
2.Период колебаний Т зависит от длины
нити / подвеса маятника, причем квадрат
периода Т пропорционален длине нити
подвеса.
Это
означает,
что
при
необходимости можно произвести расчёты
длины некоторых предметов.
3. С помощью математического маятника
можно определить ускорение свободного
падения тел вблизи поверхности Земли.

15.

СПАСИБО ЗА ВНИМАНИЕ!