Похожие презентации:
Второй замечательный предел
1.
Рассмотрим числовую последовательность1
an 1
n
n
где a1=2, a2=2.25, a3=2.37 …
Можно
предположить,
что
эта
последовательность будет возрастающей.
2.
Воспользуемся формулойm(m 1) 2 m(m 1)( m 2) 3
(1 x) 1 mx
x
x ...
2!
3!
m(m 1)...( m n 1) n
...
x
n!
m
где m – любое действительное число.
В нашем случае:
3.
11 n( n 1) 1
a n 1 1 n
2
n
n
1 2
n
n(n 1)( n 2) 1
n(n 1)...( n (n 1)) 1
3 ...
n
1 2 3
n
1 2 ... n
n
n
1
1
1
1
2
2
1
1 1 ...
1 2
n 1 2 3
n
n
1
1
2
n 1
...
1 1 ... 1
1 2 3 ... n
n
n
n
4.
Видно, что с ростом n увеличивается числоположительных слагаемых, которых всего
будет n+1, и растет величина каждого
слагаемого, т.е.
a1 a2 a3 ... an ...
Это значит, что данная последовательность
возрастает.
Теперь
покажем,
ограниченной.
что
она
является
Поскольку каждая скобка меньше единицы,
отбрасываем эти скобки и получаем
неравенство:
5.
11
1
an 2
...
1 2 1 2 3
1 2 3 ... n
Теперь каждую дробь в правой части
заменяем большей дробью с двойкой в
знаменателе:
1
1
2
1 2 3 2
1
1
...
n 1
1 2 3 ... n 2
Получаем:
1 1
1
an 2 2 ... n 1
2 2
2
6.
Сумма1 1
1
2 ... n 1
2 2
2
есть сумма n-1 членов геометрической
прогрессии, где первый член
и знаменатель
1
a1
2
1
q
2
По формуле суммы членов геометрической
прогрессии имеем:
7.
1 1n 1 1
n 1
a1 (q 1) 2 2
1
S n 1
1 n 1 1
1
q 1
2
1
2
Т.к. Sn-1<1, то
n
1
an 1 2 1 3
n
Действительно, данная последовательность
является ограниченной.
8.
Согласно признаку существования предела,монотонная
и
ограниченная
последовательность имеет предел.
Числом е или вторым замечательным
пределом называется предел
числовой последовательности
n
1
lim
1
e
n
n
9.
е – число Эйлерае=2,718281…
Можно показать, что функция
1
f ( x) 1
x
при
x
x
где х пробегает все значения, а не только
целые, тоже имеет предел, равный е:
10.
x1
lim
1
e
x
x
11.
1Пусть y
x
, тогда
lim 1 y e
y 0
1
y
12.
1Вычислить
5
lim 1
x
x
3x
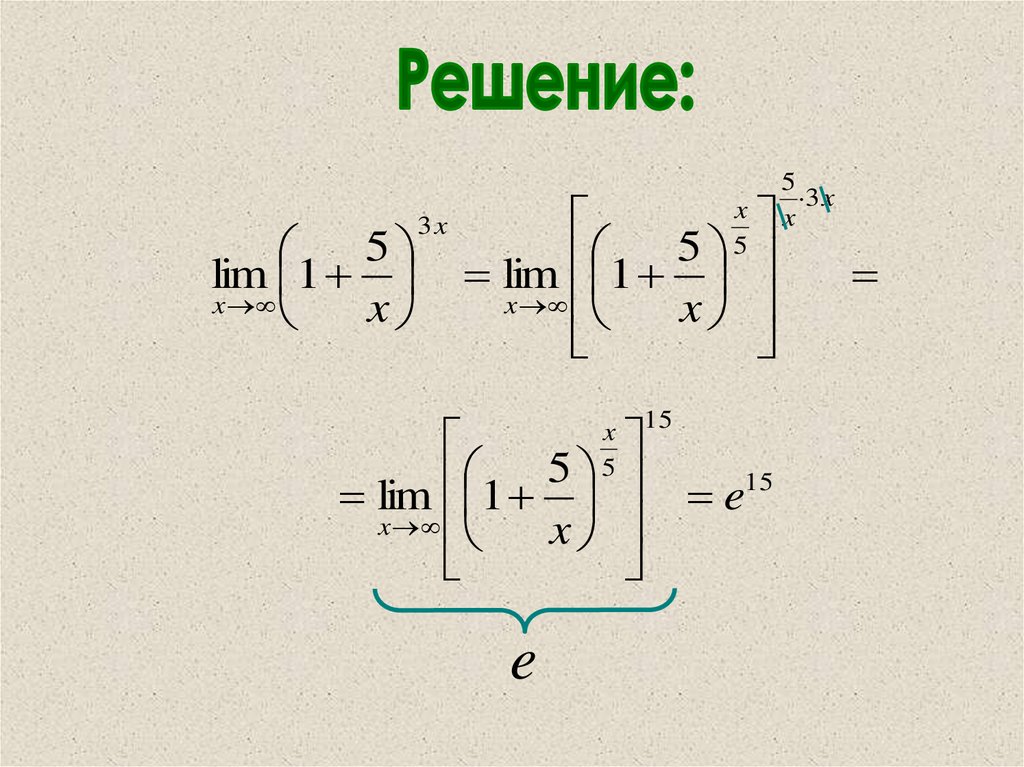
13.
5lim 1
x
x
3x
x
5
5
lim 1
x
x
5
lim 1
x
x
x
5
e
15
e15
5
3 x
x
14.
2Вычислить
lim
1
3
y
y 0
2
y
15.
lim 1 3 yy 0
2
y
1
lim 1 3 y 3 y
y 0
lim 1 3 y
y 0
1
3y
e
2
3 y
y
6
e
6
16.
3В качестве еще одного примера
рассмотрим задачу о непрерывном
начислении процентов.
Первоначальный вклад в банк составляет Q0
денежных единиц. Банк выплачивает
ежегодно Р % годовых.
Найти размер вклада через t лет.
При использовании простых процентов
размер
вклада
ежегодно
будет
увеличиваться на одну и ту же величину
P
Q0
100
17.
То естьP
Q1 Q0 1
100
2P
Q2 Q0 1
...
100
t P
Qt Q0 1
100
На практике часто применяются сложные
проценты. В этом случае размер вклада
ежегодно будет увеличиваться в одно и то
же число
P
раз, т.е.
1
100
18.
PQ1 Q0 1
100
2
P
Q2 Q0 1
...
100
t
P
Qt Q0 1
100
Если начислять проценты не один, а n раз в
году, то при ежегодном приросте Р %, процент
начисления за 1/n часть года составляет Р/n
%.
Тогда размер вклада за
начислениях составит
t
лет
при
nt
19.
PQt Q0 1
100 n
nt
Будем полагать, что проценты по вкладу
начисляются
каждое полугодие (n=2),
ежеквартально (n=4), ежемесячно (n=12),
каждый день (n=365), каждый час (n=8760)
и далее непрерывно x
Тогда размер вклада за t лет составит
nt
nt
P
P
Qt lim Q0 1
Q0 lim 1
n
n
100n
100n
20.
100nP
P
Q0 lim 1
n
100n
P
nt
100n
Q0 e
Pt
100
Qt
e
Эта формула выражает показательный
(экспоненциальный) рост (при P>0) или
убывание
(при
P<0).
Погрешность
вычисленной суммы вклада по формуле
непрерывного начисления процентов по
сравнению с формулой сложных процентов
оказывается незначительной (около 2.5 %).



















 Математика
Математика








