Відновлення повної фази

1.

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ
«КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ ІМ. І. СІКОРСЬКОГО»
Доповідь на тему:
«Моделювання процесу відновлення повної фази
сигналу при двокоординатній реєстрації
інформації в системах автоматизованого
неруйнівного контролю»
Автор роботи: В.П. Малько, студ. гр. ПК-11мн
Доповідач:
Малько В.П. студент 2 курсу магістратури, ПК-11мн.
Науковий керівник – д.т.н професор Куц Ю.В.
Контактні данні: [email protected]
Київ - 2022
1

2.

Зміст презентації
● Вступ
● Постановка задачі відновлення повної фази
● Вихідні дані моделювання
● Обгрунтування параметрів системи СЗК
● Методика проведення модельного експерименту
● Методика визначення координат положення в двоокоординатній системі
реєстрації інформації
● Методика відновлення повного фазового зсуву сигналів
● Визначення похибок відновлення повного фазового зсуву сигналів
● Висновки
2

3.

Вступ
1. Поняття фазового методу та повної фази сигналу;
2. Необхідні умови для відновлення фази сигналу;
3. Використання відновленого значення для визначення координат
первинного перетворювача дефектоскопу.
Рис.1. Формула гармонічних сигналів в фазовому методі, де U1,
U2 – амплітуди сигналів, ω – кругова частота, T – час
спостереження сигналів.
Рис.2. Формула визначення
повного зсуву фази та умова
однозначного відновлення
сигналу, де D - відстань, λ довжина хвилі.
3

4.

Постановка задачі відновлення повної
фази
Мета: Необхідно за результатами оцінених фазових зсувів сигналів в межах
Мета:
моделювання
відновлення
повної
фази сигналу
та
інтервалу
[0,Провести
2π) відновити
повну фазу
сигналу, що
утворюється
при його
визначитинапохибку
відновлення
повної фази
сигналу вта
системі
поширенні
дистанції
від випромінювача
до приймача
оцінити похибку
двокоординатної
реєстрації при використанні
системи
залишкових
класів
сигналу
в системі двокоординатної
реєстрації при
використанні
системи
(СЗК).
залишкових
класів (СЗК).
4

5.

Вихідні дані моделювання
Площина моделювання - квадрат розмірами 1x1 м.
Дискретний крок : 1 мм (0.001 м).
Довжина бази b: 1 м.
Метод визначення координат – багаточастотний акустичний фазовий
метод.
Кількість робочих частот – три.
Метод усунення неоднозначності фазових вимірювань – метод на основі
СЗК.
5

6.

Обгрунтування параметрів системи
СЗК
Модулі системи СЗК mi : m1=11, m2=13, m3=15;
Ортонормовані базиси Bi : B1=1365, B2=495, B3=286;
Робочі частоти fi : f1=30 кГц, f2=25.5 кГц, f3=22 кГц;
Дискрети визначення фазових зсувів на частотах fi :
Δφ1 = 0.571 рад, Δφ1 = 0.483 рад, Δφ1 = 0.419 рад.
6

7.

Методика проведення модельного
експерименту
1. Методика визначення координат положення в двоокоординатній
системі реєстрації інформації;
2. Методика відновлення повного фазового зсуву сигналів;
3. Визначення похибок відновлення повного фазового зсуву сигналів.
7

8.

Методика визначення координат
положення в двоокоординатній системі
реєстрації інформації
В точці Ci розташований первинний
перетворювач дефектоскопа з
встановленим випромінювачем.
Відстані між випромінювачами та
приймачем представляють собою
довжини сторін a та c трикутника ABC, з
основою b, яка дорівнює базі тобто
відстанями між приймачами.
Рис.3. Визначення координат т.С(х,у) через
трикутник
8

9.

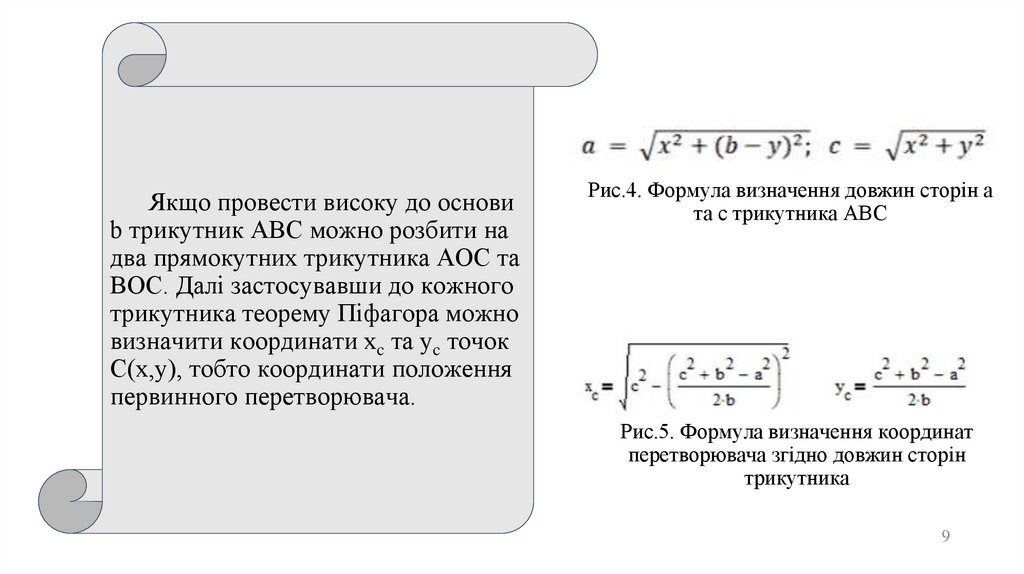
Якщо провести високу до основи
b трикутник ABC можно розбити на
два прямокутних трикутника AOC та
BOC. Далі застосувавши до кожного
трикутника теорему Піфагора можно
визначити координати xc та yc точок
C(x,y), тобто координати положення
первинного перетворювача.
Рис.4. Формула визначення довжин сторін a
та c трикутника ABC
Рис.5. Формула визначення координат
перетворювача згідно довжин сторін
трикутника
9

10.

Методика відновлення повного
фазового зсуву сигналів
1. Задання сітки координат;
2. Розрахунок параметрів СЗК та довжин сторін a та c (рис.4);
3. Розрахунок повного фазового зсуву сигналів та початкових фазових зсувів;
4. Розрахунок залишків ai та ci СЗК для сторін a та c;
5. Відновлення повного фазового зсуву згідно отриманих залишків;
6. Перевірка правильності відновлення повного фазового зсуву.
10

11.

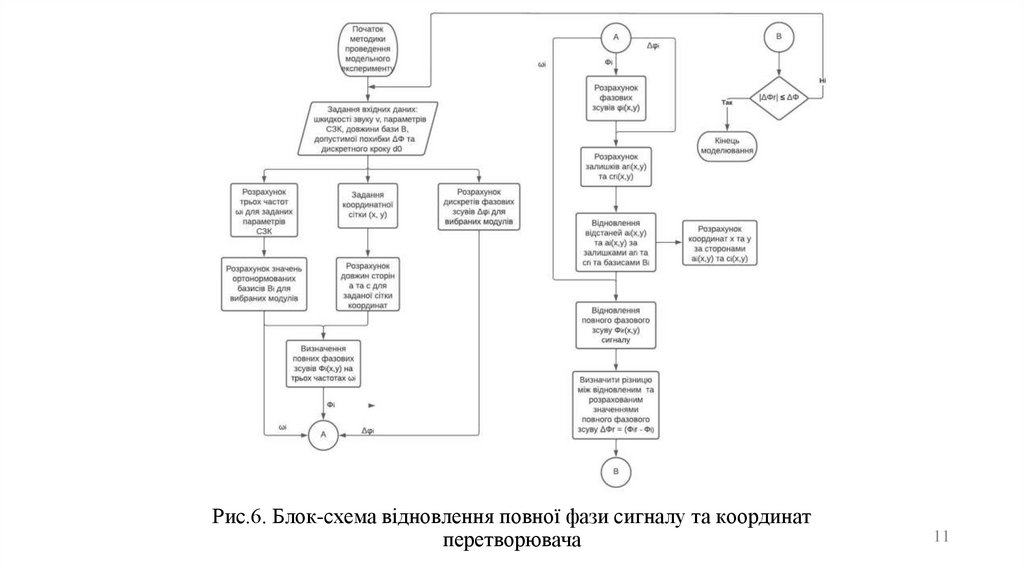
Рис.6. Блок-схема відновлення повної фази сигналу та координат
перетворювача
11

12.

Визначення похибок відновлення
повного фазового зсуву сигналів
Похибки відновлення сигналу
розраховується як різниця між відновленим
та розрахованим значенням. Саме від
розміру похибки відновлення можно судити
про правильність роботи методики.
Рис.7. Похибки відтворення повної фази
сигналу для сторін a та c
12

13.

Висновок
Проаналізована можливість відновлення повної фази сигналу за допомогою
системи залишкових класів. Наведена блок-схема алгоритму реалізації моделювання
відновлення повної фази за допомогою СЗК. Проаналізувавши графіки моделювання
була визначена похибка відтворення повної фази, яка становить ±0.3 рад. В реальний
системах НК на визначення координат впливають шуми, тому необхідно провести
модельні експерименти відновлення повної фази за їх наявності. Для гарантування
розрізнення кожної з точок необхідно визначити мертві зони, в яких неможливо
розрізнити координати двох сусідніх точок. Також з метою підвищення точності
визначення координат необхідно виконувати калібрування системи по
швидкості ультразвуку, яка є функцією від метеопараметрів.
13

14.

Дякую за увагу
12