Похожие презентации:
Описание подхода по увеличению скорости расчётов
1.
ОПИСАНИЕ ПОДХОДА ПО УВЕЛИЧЕНИЮСКОРОСТИ РАСЧЁТОВ
Соколовский Андрей
Галушко Сергей
22 Декабря 2022
2.
МОТИВАЦИЯПовысить скорость расчётов.
Возможность решать системы нелинейных уравнений.
Устойчивость конечного решения системы.
Возможность добавить уравнения связывающие механические
переменные с переменными типа “давление/поток”.
3.
ПРЕДПОСЫЛКИЗадвижка: 4 переменные, 2 уравнения.
Количество уравнений n зависит от количества объектов на схеме.
Вычислительная сложность метода Гаусса: .
Метод Гаусса “одноразовый”.
Деление по группам:
Пример 2 группы:
4.
4МЕТОД ГАУССА
Метод Гаусса-Жордана
5.
5LU РАЗЛОЖЕНИЕ
6.
6РАЗРЕЖЕННЫЕ МАТРИЦЫ
Для хранения матрицы нам необходимо 2 массива длины NNZ и один массив длины (N + 1).
Таким образом, вычислительная сложность нахождения разложению LU будет зависеть от
количества ненулевых элементов.
7.
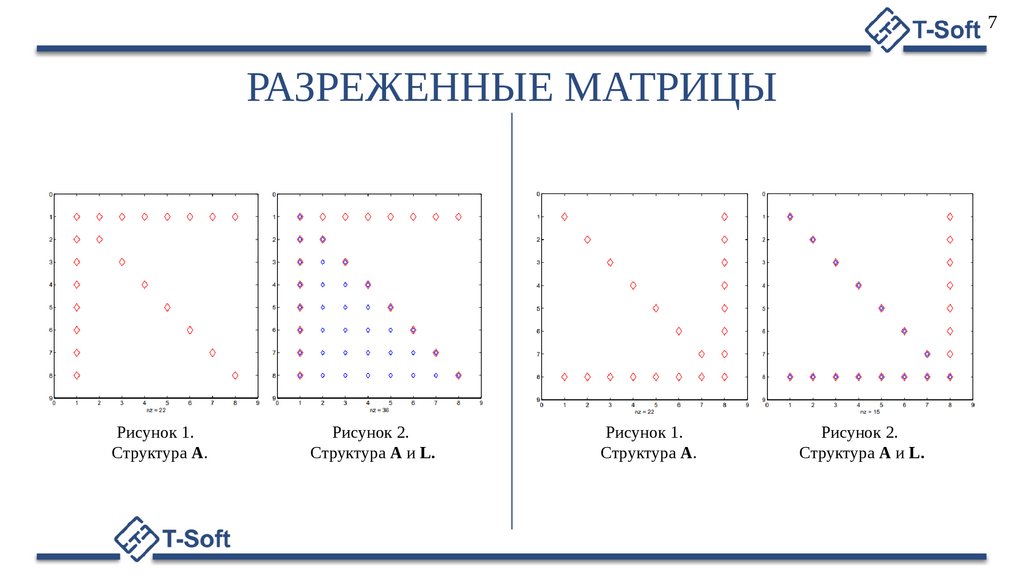
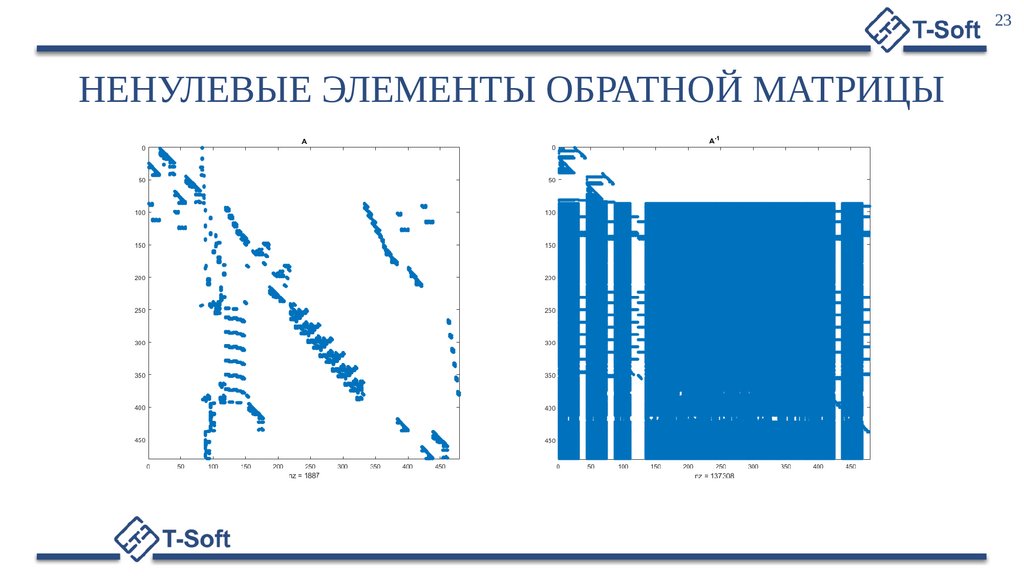
7РАЗРЕЖЕННЫЕ МАТРИЦЫ
Рисунок 1.
Структура А.
Рисунок 2.
Структура А и L.
Рисунок 1.
Структура А.
Рисунок 2.
Структура А и L.
8.
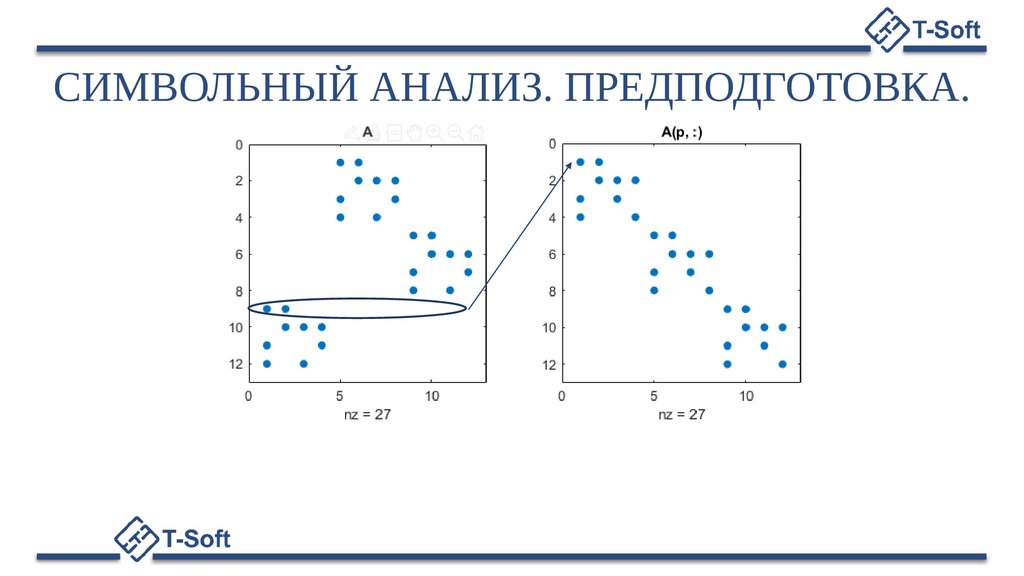
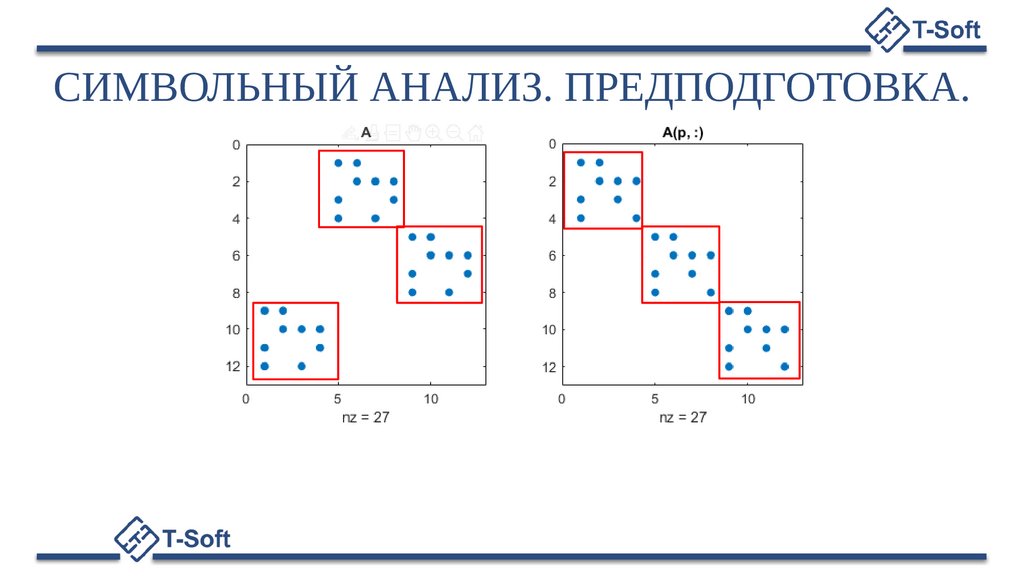
СИМВОЛЬНЫЙ АНАЛИЗ. ПРЕДПОДГОТОВКА.9.
СИМВОЛЬНЫЙ АНАЛИЗ. ПРЕДПОДГОТОВКА.10.
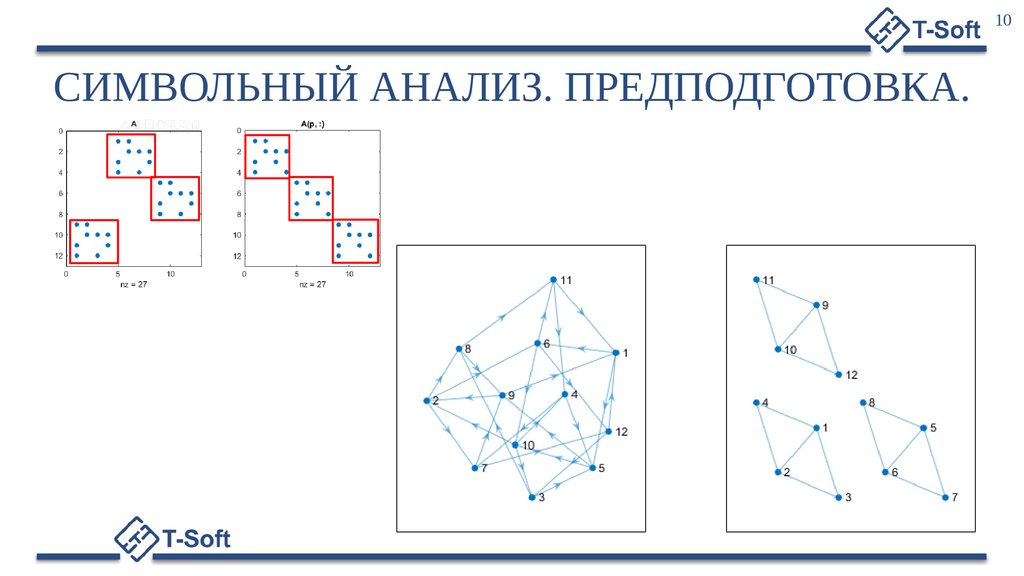
10СИМВОЛЬНЫЙ АНАЛИЗ. ПРЕДПОДГОТОВКА.
11.
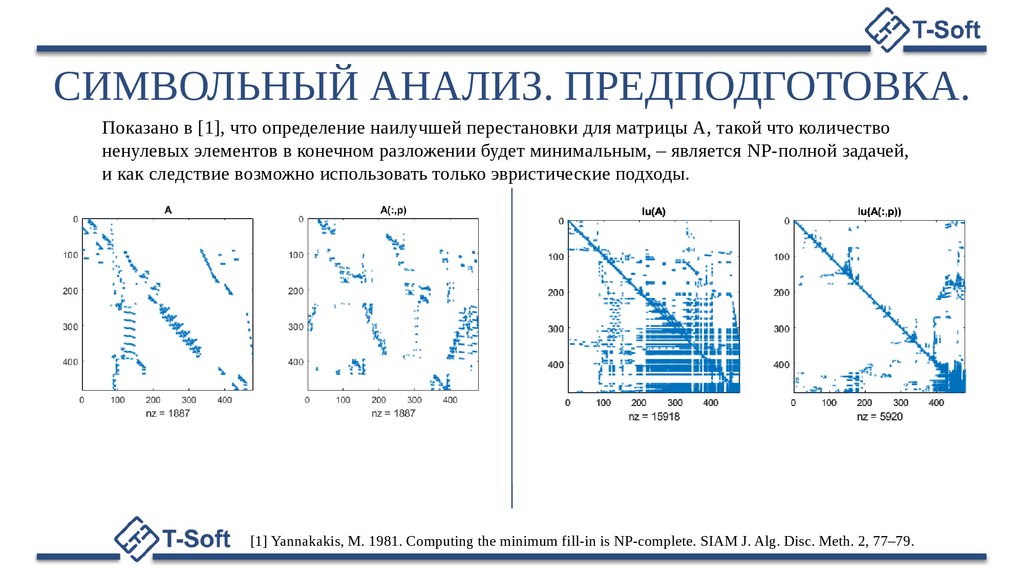
СИМВОЛЬНЫЙ АНАЛИЗ. ПРЕДПОДГОТОВКА.Показано в [1], что определение наилучшей перестановки для матрицы A, такой что количество
ненулевых элементов в конечном разложении будет минимальным, – является NP-полной задачей,
и как следствие возможно использовать только эвристические подходы.
[1] Yannakakis, M. 1981. Computing the minimum fill-in is NP-complete. SIAM J. Alg. Disc. Meth. 2, 77–79.
12.
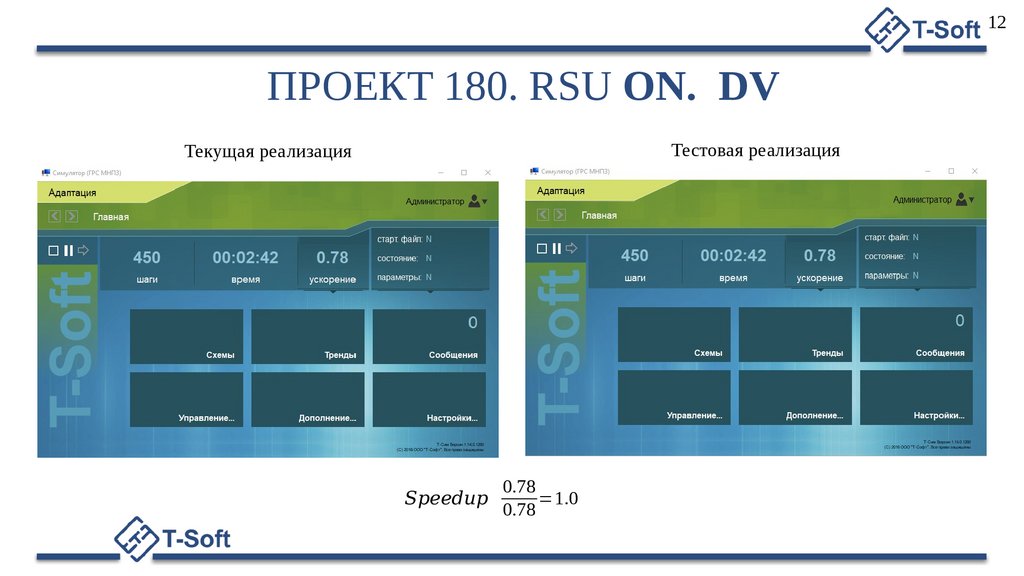
12ПРОЕКТ 180. RSU ON. DV
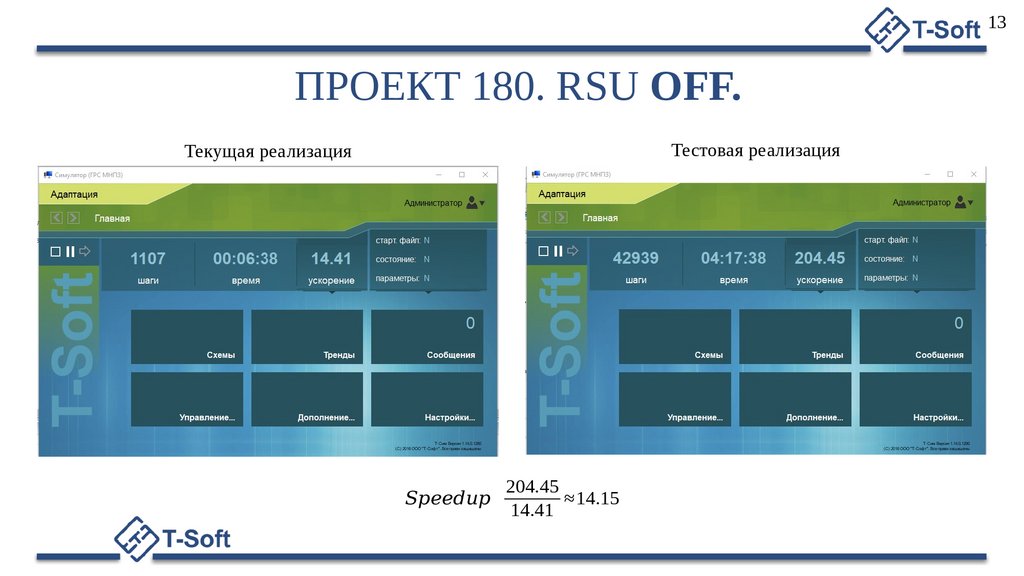
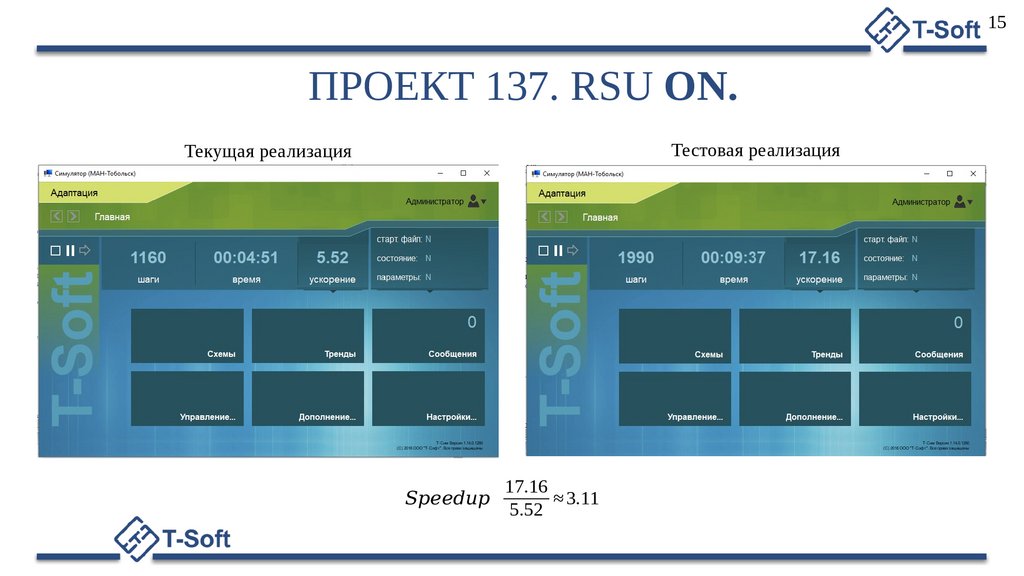
Тестовая реализация
Текущая реализация













 Математика
Математика








